基于DSC和MLP的欠驅動船舶自適應滑模軌跡跟蹤控制

沈智鵬, 王 茹

(大連海事大學信息科學技術學院, 遼寧 大連 116026)

0 引 言

船舶運動控制是控制理論應用于航海領域的一個重要的研究課題,船舶運動的目的在于提高船舶自動化水平,進而能夠保證船舶在航行過程中的安全性、經濟性以及舒適性[1]。目前,海上航行的大多數船舶僅裝備螺旋槳主推進器和舵裝置用以船舶推進和操縱,是一類典型的欠驅動系統。欠驅動船舶的鎮定控制、路徑和軌跡跟蹤控制等問題一直是不少船舶運動控制理論研究者關注的熱點。

近年來,對船舶航跡跟蹤控制問題的研究,已有諸多成果。如文獻[2-3]基于Lyapunov直接法和坐標轉換,在保證航向角速度滿足標準持續激勵條件下,設計船舶軌跡跟蹤控制律。這些控制律的設計都必須保證船舶模型參數是已知的。此外,文獻[4-5]基于backstepping思想設計船舶航跡跟蹤控制律,實現了對船舶軌跡跟蹤的有效控制。文獻[6]在已知外界干擾有界的情況下,利用逆推法將船舶運動的控制律分解為兩個子回路進行設計,提出了一種基于干擾界已知的滑模控制策略。但是采用傳統的backstepping方法設計控制器存在“微分爆炸”問題,不利于工程實踐,文獻[7-9]采用動態面控制(dynamic surface control,DSC)思想,在以往backstepping技術的基礎上加入了一階低通濾波器,避免狀態量在進行微分計算時存在“微分爆炸”問題,簡化控制律設計,易于工程實踐。

然而船舶在實際航行中,除了遭受風、浪、流等外界環境干擾外,其自身的質量、速度、慣性矩等性能也會隨之變化,導致船舶模型參數也跟著發生一定的變化。為了克服船舶模型參數的不確定性和外界風、浪、流等干擾的影響,文獻[10]在控制器的設計中利用自適應神經網絡的萬能逼近特性估計船舶動態不確定,并根據Lyapunov穩定性原理證明船舶閉環系統中所有信號一致最終有界。文獻[11]針對欠驅動船舶的路徑跟蹤問題,設計了神經網絡穩定自適應控制器,并對風、浪、流等外界環境干擾進行自適應補償。文獻[12]為實現在參數攝動和外界環境干擾影響下對船舶路徑跟蹤的控制,運用滑模和神經網絡這兩種技術設計了一種基于神經滑模魯棒控制器。文獻[13]在欠驅動船舶的路徑跟蹤問題上,利用神經網絡算法對強化學習的參數進行優化,增強了所設計控制器的自適應性。文獻[14]針對無人水面艇的航跡跟蹤問題,在無人艇存在建模誤差以及外界干擾的情況下,利用神經網絡技術,設計出一種自適應徑向基函數(radial basis function,RBF)神經網絡控制器,該控制器具有較強的魯棒性。不過,采用神經網絡技術需要在線估計神經網絡的權值向量,不可避免的增加了控制算法的計算負載,也就是所謂的“維數災難”問題。這一問題可以采用最小學習參數(minimal learning parameter,MLP)方法[15]予以解決。MLP法是通過在線估計神經網絡權值向量范數,從而使得所提出的自適應律不依賴于神經網絡節點數。文獻[16]在對大氣變化非常敏感的超音速飛行器中,采用DSC和MLP結合起來設計控制器,利用簡單的自適應算法就能夠實現對動態不確定的估計,在線更新計算負擔大大減少。文獻[17]將采用MLP代替神經網絡控制算法,應用于三自由度欠驅動船舶上,從而降低了該控制算法的計算負擔,最后,通過Lyapunov原理證明了所設計控制律的有效性。

考慮欠驅動船舶軌跡跟蹤存在模型參數不確定以及在實際航行中不可避免的遭受外部環境干擾的問題,設計了一種自適應神經網絡滑模控制方法。通過引入DSC技術避免傳統backstepping方法帶來“微分爆炸”問題,采用MLP方法用于避免“維數災難”問題,并以單參數在線學習代替所有權值在線學習,從而使其計算負載降低,更符合工程要求。利用Lyapunov穩定性原理證明所設計控制律可使欠驅動船舶沿期望軌跡航行,并保證欠驅動船舶軌跡跟蹤閉環系統中軌跡跟蹤誤差信號一致最終有界,最后利用一艘“BAY CLASS”遠程巡邏船的仿真實驗對所設計控制器的有效性進行分析和驗證。

1 問題描述

考慮船舶前向、橫蕩和艏搖3個自由度的水平面運動,則存在模型參數不確定性和外界環境干擾影響的欠驅動水面船舶的運動學和動力學模型可表示為

(1)

式中

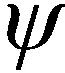
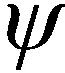
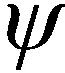
為實現欠驅動船舶軌跡控制律的設計,引入以下假設。

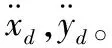
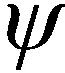
控制目標：針對三自由欠驅動船舶非線性數學模型(1),在滿足假設1和假設2的條件下,考慮船舶存在模型不確定和外界環境干擾的情況,設計前向推進力τu和轉向力矩τr使得所設計船舶能夠沿期望軌跡航行,并保證船舶系統中軌跡跟蹤誤差信號一致最終有界,實現對欠驅動船舶軌跡跟蹤的有效控制。

2 自適應滑模軌跡跟蹤控制律設計

為后續設計船舶系統控制律的需要,定義誤差變量

(2)

式中,(xd,yd)為船舶的參考軌跡;xe、ye分別為縱向位置誤差和橫向位置誤差;ue、ve分別為前向速度誤差和橫漂速度誤差,根據船舶的參考軌跡和實際位置信息可設計虛擬控制律。

為了實現對船舶軌跡跟蹤位置誤差趨于零,對式(2)中的xe和ye求導可得

(3)

并將ue和ve代入式(3)得

(4)

設計虛擬控制律，即

(5)

式中,k1、k2>0為設計常數。

將式(5)代入到式(4)可得

(6)

即

(7)

由式(7)可知,當ue、ve收斂于零時

(8)

由式(8)可知,位置誤差xe、ye將收斂于零,即實現對船舶軌跡跟蹤的控制。

2.1 縱向推力的最小參數自適應滑模控制律設計

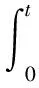
(9)

式中,λ1>0為設計常數。

對一階滑模面(9)求導可得

(10)

從式(10)可以看出,如果采用傳統的backstepping對虛擬控制量αu直接求導,將會增加計算復雜程度。為了解決這個問題,依據動態面控制思想[18],對αu引入一階低通濾波器,并設新的狀態量Xu∈R為一階濾波器的輸出,其數學表達式為

(11)

式中,T1>0為濾波時間常數。

(12)

所產生的濾波誤差為y1=Xu-αu。

對y1關于時間求導,結合式(5)和式(12)得

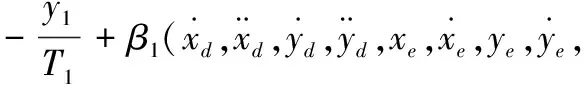
(13)

式中,β1(·)為非線性連續函數。

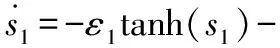
(14)

式中,ε1>0,η1>0為設計常數。

由于式(14)中的fu存在有船舶動態不確定項,不能直接用于控制律的設計,故采用RBF神經網絡控制算法對未知項進行逼近。RBF神經網絡是一種3層前饋網絡,包括輸入層、隱含層和輸出層。RBF神經網絡自學習能力較強,可以對任意函數進行逼近,避免了對未知函數進行復雜的數學理論分析,簡化控制結構。圖1為多輸入單輸出的RBF神經網絡結構圖。

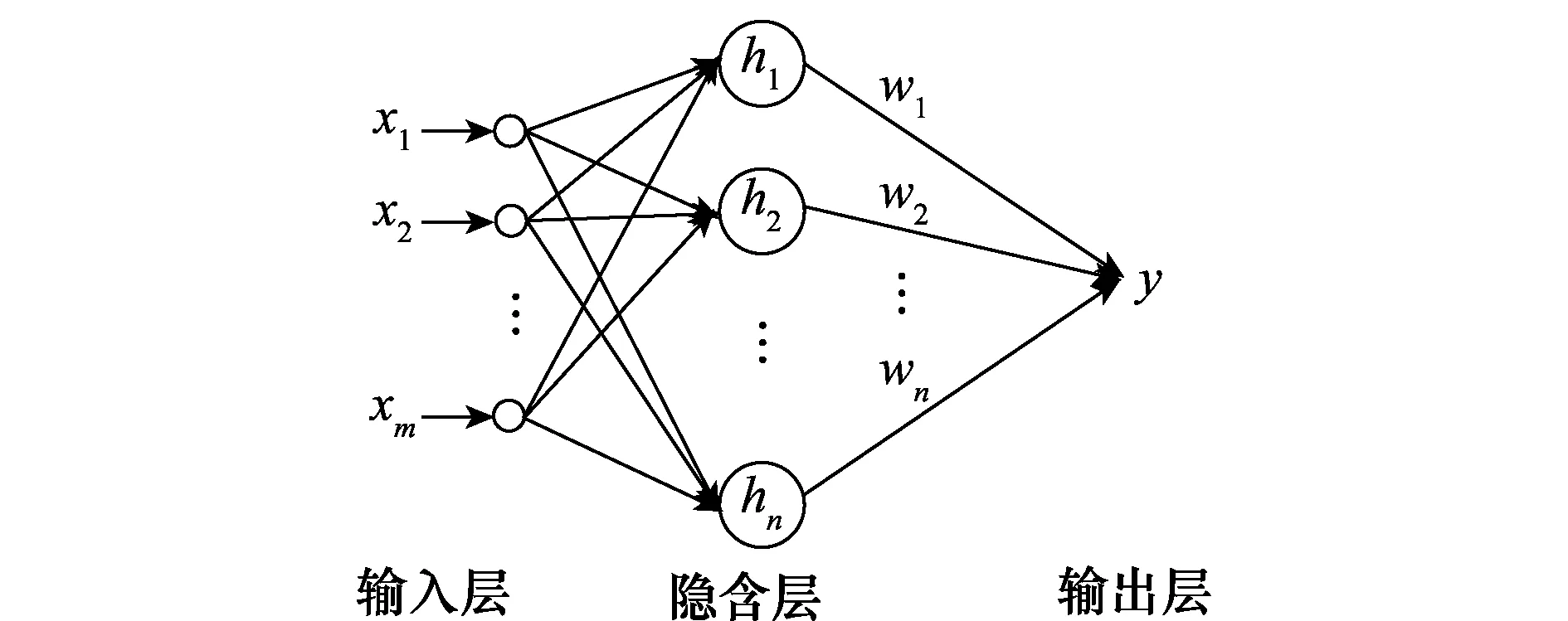
圖1 RBF神經網絡拓撲結構Fig.1 RBF neural networks topology architecture

RBF神經網絡輸入層、隱含層節點數量分別為m、n,輸出為1。x=[x1x2…xm]T∈Rm為網絡的輸入向量,則神經網絡高斯基函數的輸出表達式為

(15)

式中,bj>0為高斯基函數的寬度,j為神經網絡隱含層的第j個節點;cj=[c1,c2,…,cm]T∈Rm為第j個隱層神經元的中心點向量值,與輸入向量x的維數相同。

對于系統中的含有參數不確定函數fu的神經網絡輸出表達式為

(16)

式中,Z=[u,v,r]T為神經網絡的輸入,h(Z)=[h1(Z),h2(Z),…,hj(Z)]T為神經網絡的高斯基函數輸出;Wu∈Rj×1為神經網絡的理想權值,δ1為神經網絡的逼近誤差,且滿足|δ1|≤δU,δU為誤差的界值。

假設用于逼近fu的神經網絡權值Wu有界,即‖Wu‖≤WU,令

(17)

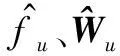
設計參數自適應律為

(18)

式中,Γu>0,ξ1>0為設計常數。根據式(17)和式(18)設計縱向推進力控制律,即

(19)

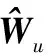
避免參數漂移的的方法有死區法和σ-修正法等,由于采用死區法要設置死區寬度,寬度過大時,會導致系統誤差趨于一個較大的死區,影響船舶閉環系統的精度,故為了克服死區問題,設計帶有“σ-修正”的單參數自適應律

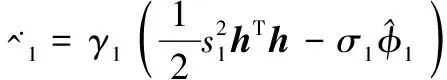
(20)

式中,γ1>0，σ1>0為設計常數。故縱向推進力控制律式(16)變換為

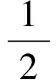
(21)

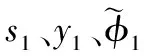
證明定義Lyapunov函數為

(22)

對于給定的正數B0、?0,考慮如下緊集:

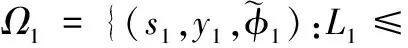
注意到Ωd×Ω1也是緊集,且非線性連續函數β1(·)在Ωd×Ω1緊集內有最大值Nu。所以

(23)

式中,α1為正常數。

對式(22)求導,并將式(10)、式(21)、式(23)代入可得

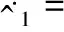
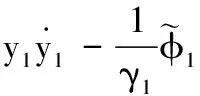
(24)

根據文獻[19]的Young’s不等式,可得式(25)和式(26)成立

(25)

(26)

可得

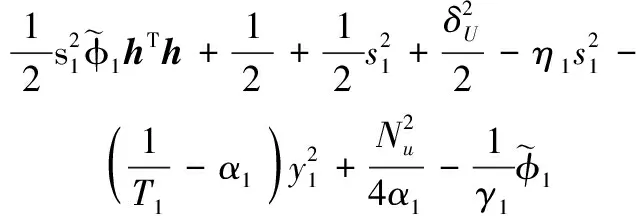
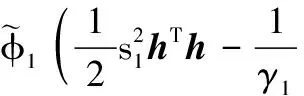
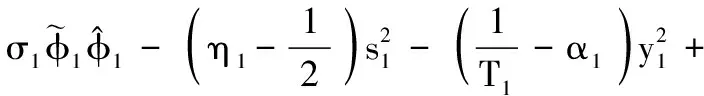
(27)

(28)

將式(28)代入到式(27)可得

(29)

式中

μ1=min{(2η1-1),2(1/T1-α1,σ1}

2η1-1>0

1/T1-α1>0

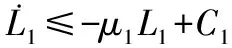
(30)

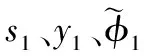
證畢

2.2 轉向力矩的最小參數自適應滑模控制律設計

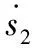
(31)

對二階滑模面式(31)求導可得

(32)

由式(5)得

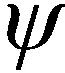
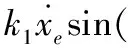
(33)

為方便后續表達式簡潔,令

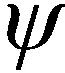
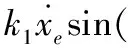
(34)

為防止對P直接求導出現項數滋升,對P引入一階低通濾波器,并設新的狀態量XP∈R為一階濾波器的輸出,其數學表達式為

(35)

式中,T2>0為濾波時間常數。

(36)

定義濾波誤差為y2=XP-P。

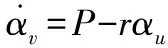
(37)

故

(38)

對y2關于時間求導,結合式(5)、式(36)得

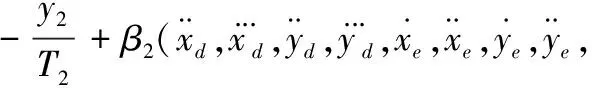
(39)

式中,β2(·)為非線性連續函數。

與前面縱向推力的自適應滑模控制律設計類似,式(38)中存在含有動態不確定的fr,采用RBF神經網絡進行逼近,表達式為

(40)

式中,Wr為神經網絡的理想權值;δ2為神經網絡的逼近誤差且|δ2|≤δR。

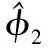
設計帶有“σ-修正”的參數自適應律為

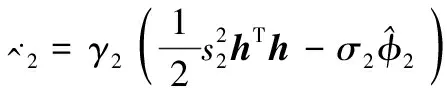
(41)

式中,γ2>0、σ2>0為設計常數。

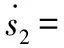
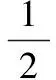
(42)

式中,ε2>0、η2>0為設計常數。

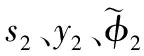
證明定義Lyapunov函數:

(43)

對于給定的正數B0、?2,考慮如下緊集

注意到Ωd×Ω2也是緊集,且非線性連續函數β2(·)在Ωd×Ω2緊集內有最大值NP。所以結合式(39)可得

(44)

式中,α2為正常數。

對式(43)求導并將式(38)、式(41)、式(42)、式(44)代入得

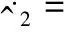
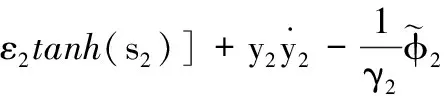
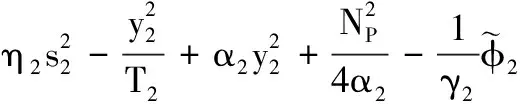
(45)

根據文獻[19]的Young’s不等式,可得式(46)和式(47)成立

(46)

(47)

代入式(45)可得

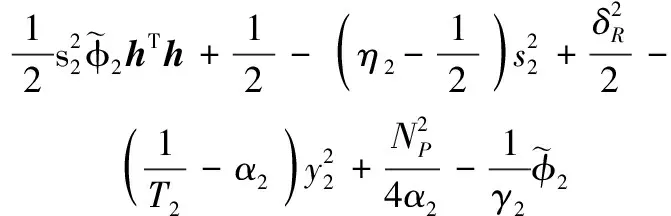
(48)

與式(28)相同,考慮不等式：

(49)

代入式(48)得

(50)

式中

μ2=min{(2η2-1),2(1/T2-α2),σ2}

2η2-1>0

1/T2-α2>0

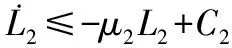
(51)

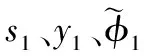
證畢

3 穩定性分析

綜上所述,通過設計縱向推力控制律τu和轉向力矩控制律τr,分別滿足了式(30)和式(50)可達條件,保證系統運動狀態可在有限時間內趨向并保持在相應的滑模面s1和s2,同時所設計的兩個滑模面是漸進收斂于原點的。所以系統運動點也會以指數速率收斂于原點,即滿足

(52)

當速度誤差ue、ve趨于0時,由式(8)可知,位置誤差xe、ye也將趨于0,故船舶運動的實際軌跡能夠很好沿參考軌跡航行。

為證明船舶的艏搖角速度r是有界輸入有界輸出,定義如下Lyapunov函數:

(53)

由船舶模型式(1)可知

(54)

式中,Δfr為船舶動態未知不確定項,其他項為已知項,本文對fr進行了逼近,故Δfr可由式(54)得到,后續證明可直接應用Δfr。

對式(53)求導得

m33Δfr+br+τr]

(55)

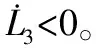
4 仿真研究

為了驗證本文所設計的帶“σ-修正”的DSC和MLP自適應滑模控制方法的有效性,應用文獻[20]中一艘單槳單舵的遠程巡邏船進行仿真研究,該船長為38 m,質量為m=118×103kg,其他參數為m11=120×103kg,m22=177.9×103kg,m33=636×105kg,du=215×102kg/s,dv=147×103kg/s,dr=802×104kg/s,du2=0.2,du,du3=0.1,du,dv2=0.2dv,dv3=0.1dv,dr2=0.2dr,dr3=0.1dr,系統的不確定性部分取為

外界風浪流產生的干擾力和力矩取為

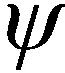
應用本文設計的基于DSC和MLP的自適應滑模控制器進行船舶軌跡跟蹤控制,仿真結果如圖2～圖8所示。圖2表示選用兩種不同的算法欠驅動船舶參考軌跡曲線xd、yd和實際運動軌跡曲線x、y。從圖2中曲線可以看出，本文算法可以使船舶快速的跟蹤上參考軌跡,并且保持穩定跟蹤狀態,具有較好的跟蹤能力,而采用文獻[6]中的算法基本上能跟蹤上參考軌跡,并且所用的時間較長。圖3和圖4分別為位置誤差收斂曲線和速度誤差收斂曲線,從圖3、圖4中可以看出,位置誤差和速度誤差都基本收斂于零,但采用滑模控制算法的位置誤差xe和速度誤差ue、ve在零附近波動較大,從位置誤差ye曲線圖可以看出采用滑模控制算法需200 s能夠跟蹤預期的軌跡,采用本文算法40 s就可以使船舶運動在預期軌跡上航行。

圖2 初始位置在圓內的軌跡跟蹤控制Fig.2 Trajectory tracking control of the vessel with initial position inside the circle

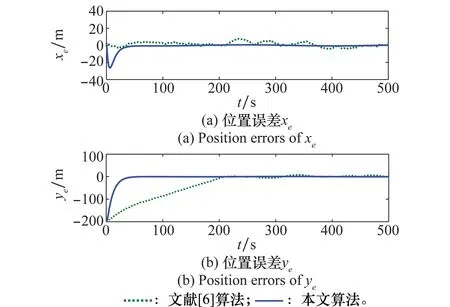
圖3 位置誤差收斂曲線Fig.3 Convergence of position errors

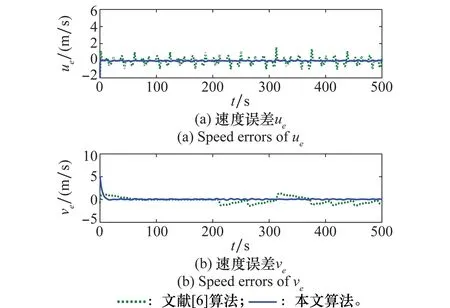
圖4 速度誤差收斂曲線Fig.4 Convergence of speed errors

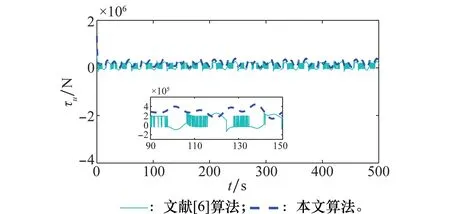
圖5 軌跡跟蹤控制輸入τu變化曲線Fig.5 Trajectory tracking control input τu curves

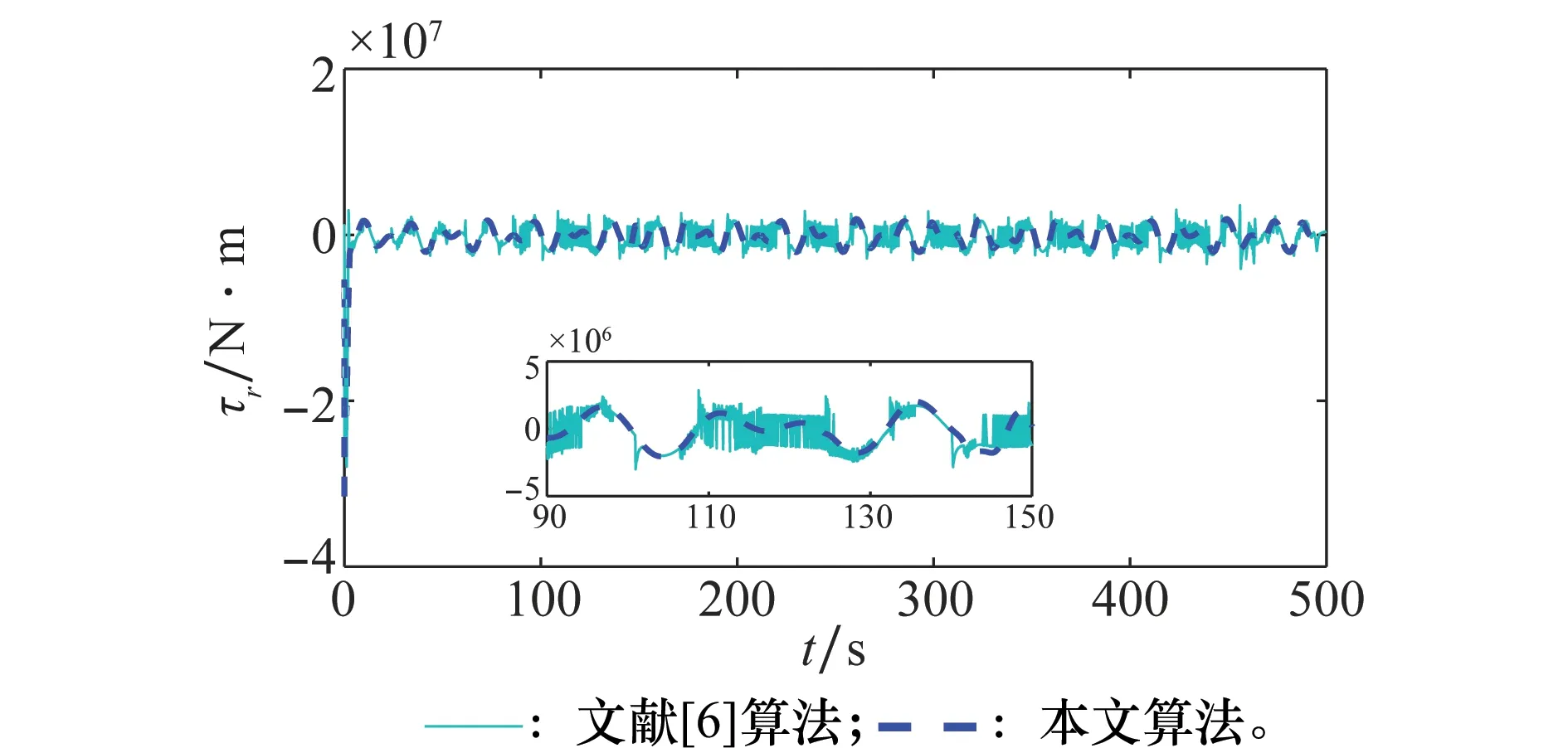
圖6 軌跡跟蹤控制輸入τr變化曲線Fig.6 Trajectory tracking control input τr curves

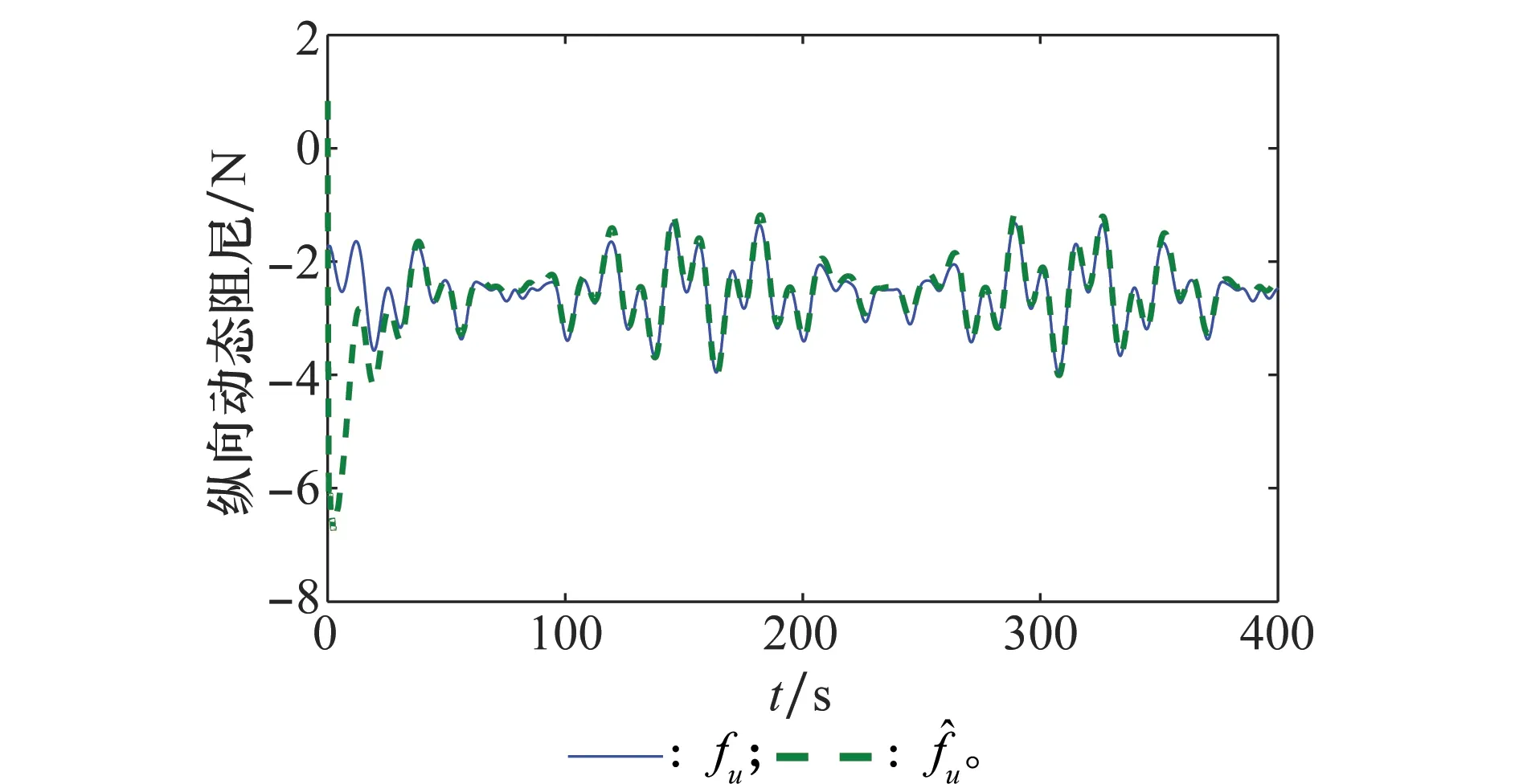
圖7 縱向動態阻尼的逼近曲線 Fig.7 Approximation curve of surge dynamic damping

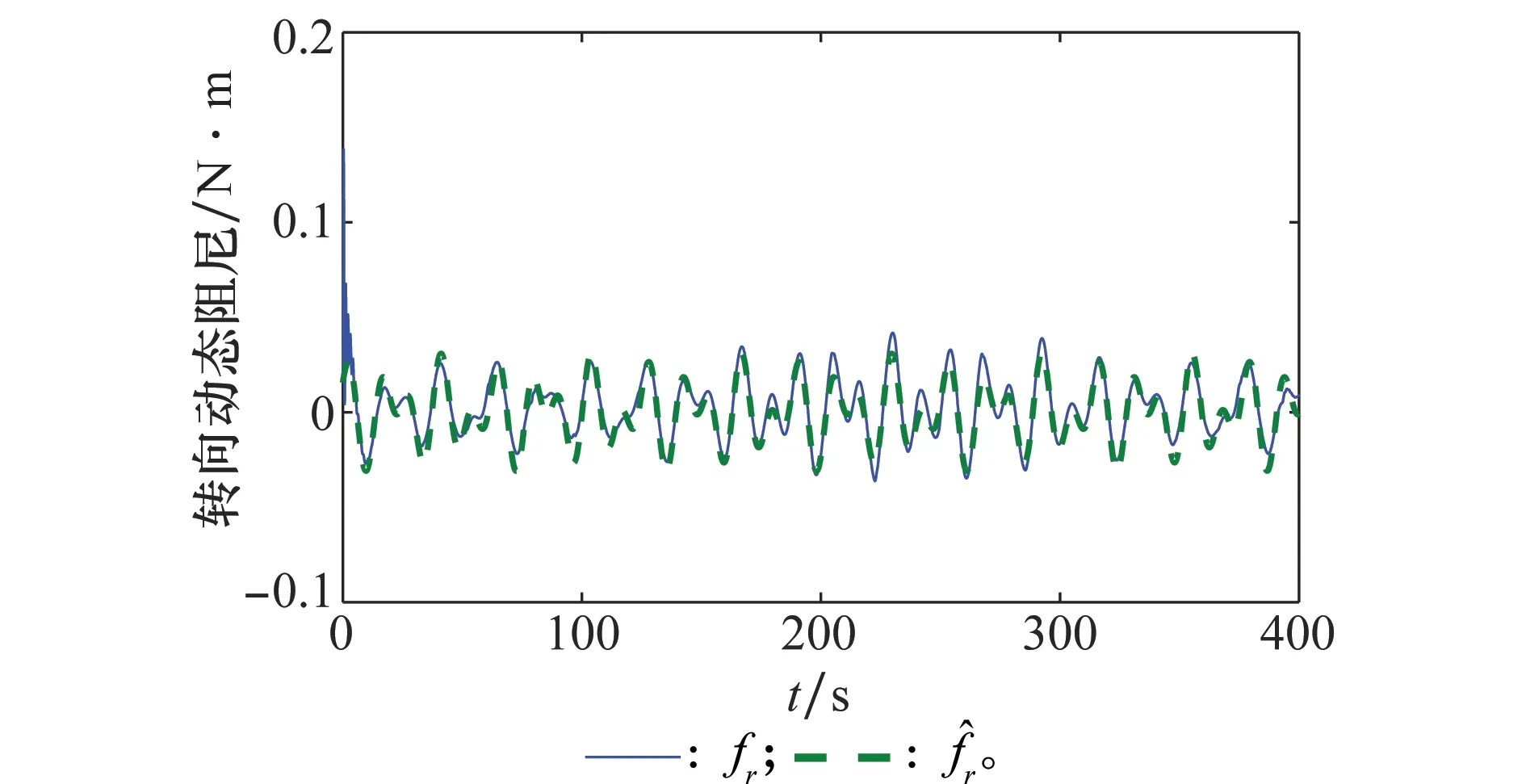
圖8 轉向動態阻尼的逼近曲線Fig.8 Approximation curve of yaw dynamic damping

圖5和圖6為船舶的控制輸入,表明采用本文算法轉向力矩τr在前10 s有抖振現象是由于船舶起始點偏離參考軌跡初始位置較大造成的,經過一段時間的調節后變為光滑的曲線,符合實際的控制要求。采用滑模控制算法使船舶系統的控制輸入出現抖振現象,而且不可消除。圖7和圖8表示不確定函數fu和fr的真實值和估計值,從圖中可以看出帶有“σ-修正”的MLP能很好地估計船舶模型參數中的動態變量。

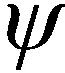
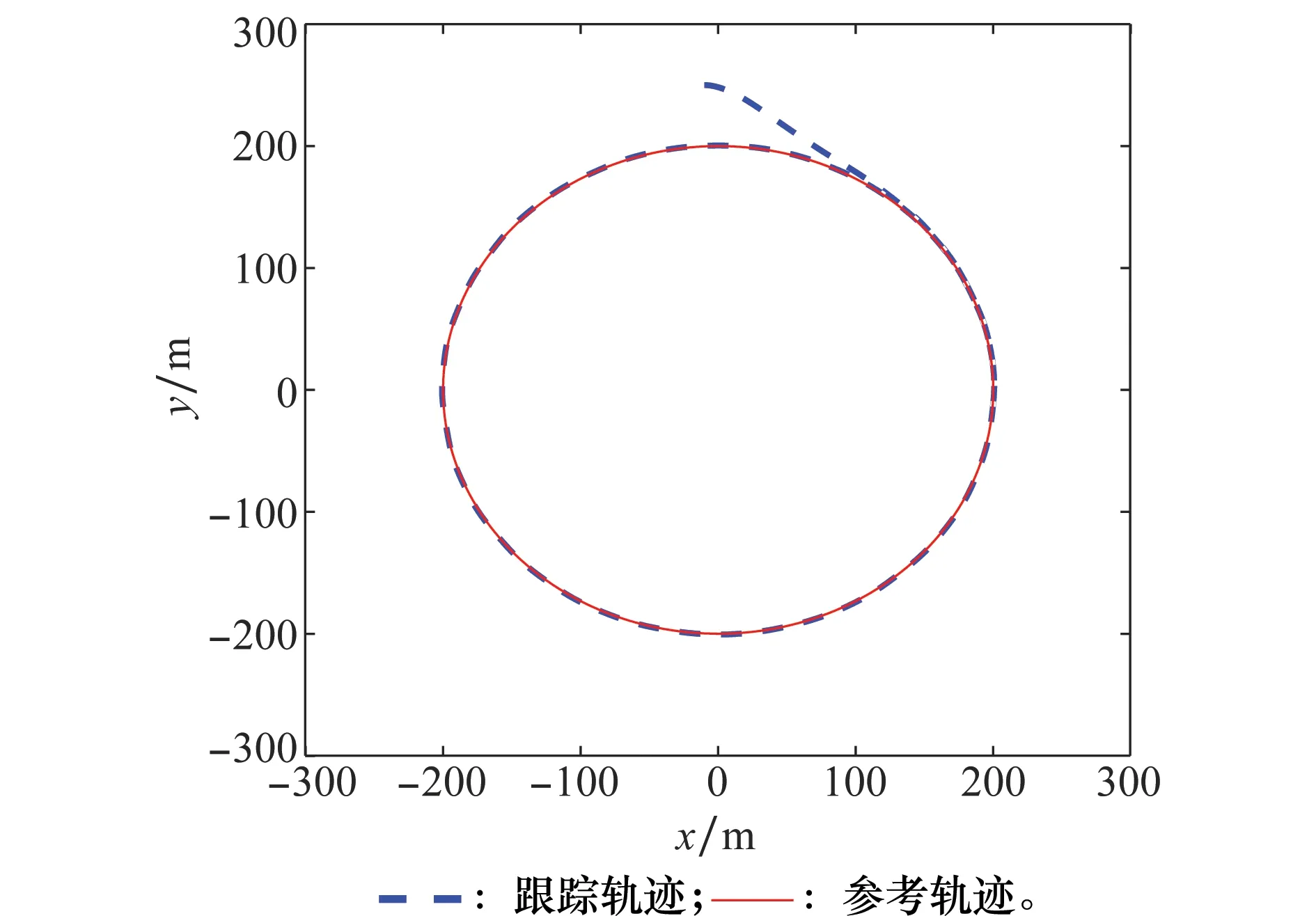
圖9 初始位置在圓外的軌跡跟蹤控制Fig.9 Trajectory tracking control of the vessel with initial position inside the circle

5 結 論

針對欠驅動船舶存在模型參數不確定和外界環境干擾的軌跡跟蹤控制問題,提出了一種基于DSC和MLP的自適應滑模控制方法。該方法克服了文獻[6]模型參數先驗知識的局限性,并消除了符號函數帶來的抖振問題。引入DSC的目的是為了避免傳統的backstepping方法對虛擬控制直接求導存在的“微分爆炸”問題,采用帶有“σ-修正”的MLP以單參數在線學習代替神經網絡控制算法中所有權值在線學習,既減少控制律的計算量,避免出現“維數災難”問題,又能防止參數漂移,易于工程實踐,仿真結果證明了該算法的有效性。

[1] FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. New York: Wiley,2011.

[2] JIANG Z P. Global tracking control of underactuated ships by Lyapunov’s direct method[J].Automatica,2002,38(2):301-309.

[3] DONG W J,GUO Y. Nonlinear tracking control of underactuated surface vessel[C]∥Proc.of the IEEE American Control Conference, 2005:4351-4356.

[4] GHOMMAM J,MNIF F,BENALI A,et al. Asymptotic back stepping stabilization of an underactuated surface vessel[J]. IEEE Trans.on Control Systems Technology,2006,14(6):1150-1157.

[5] S?RENSEN M E N,BJ?RNE E S,BREIVIK M. Performance comparison of backstepping-based adaptive controllers for marine surface vessels[C]∥Proc.of the IEEE Control Applications,2016:891-897.

[6] 朱齊丹,于瑞亭,夏桂華,等. 風浪流干擾及參數不確定欠驅動船舶航跡跟蹤的滑模魯棒控制[J]. 控制理論與應用,2012,29(7):959-964.

ZHU Q D,YU R T,XIA G H,et al. Sliding-mode robust tracking control for underactuated surface vessels with parameter uncertainties and external disturbances[J]. Control Theory & Applications,2012,29(7):959-964.

[7] AMEZQUITA S K,YAN L,BUTT W A,et al. Dynamic surface control for a class of nonlinear feedback linearizable systems with actuator failures[J]. IEEE Trans.on Neural Networks & Learning Systems,2017,28 (9):2209-2214.

[8] 杜佳璐,楊楊,胡鑫,等. 基于動態面控制的船舶動力定位控制律設計[J]. 交通運輸工程學報,2014,14(5):36-42.

DU J L,YANG Y,HU X,et al. Control law design of dynamic positioning for ship based on dynamic surface control[J]. Journal of Traffic and Transportation Engineering,2014,14(5):36-42.

[9] 王昊,王丹,彭周華,等. 多自主船協同路徑跟蹤的自適應動態面控制[J]. 控制理論與應用,2013,30(5):637-643.

WANG H,WANG D,PENG Z H,et al. Adaptive dynamic surface control for cooperative path following of multiple autonomous surface vessels[J]. Control Theory & Applications,2013,30(5):637-643.

[10] DU J L,HU X,LIU H B,et al. Adaptive robust output feedback control for a marine dynamic positioning system based on a high-gain observer[J]. IEEE Trans.on Neural Networks & Learning Systems,2015,26(11):2775-2786.

[11] 劉楊,郭晨,沈智鵬,等.欠驅動船舶路徑跟蹤的神經網絡穩定自適應控制[J]. 控制理論與應用,2010,27(2):169-174.

LIU Y,GUO C,SHEN Z P,et al. Stable adaptive neural network control of path following for underactuated ships[J]. Control Theory & Applications,2010,27(2):169-174.

[12] 楊震,劉繁明,王巖. 欠驅動船舶路徑跟蹤的神經滑模控制[J]. 中國造船,2015,56(2):45-55.

YANG Z,LIU F M,WANG Y. Path following of underactuated surface vessels based on neural sliding mode[J]. Shipbuilding of China,2015,56(2):45-55.

[13] 沈智鵬,代昌盛. 欠驅動船舶路徑跟蹤的強化學習迭代滑模控制[J]. 哈爾濱工程大學學報,2017,38(5):697-704.

SHEN Z P,DAI C S. Iterative sliding mode control based on reinforced learning and used for path tracking of underactuated ship[J].Journal of Harbin Engineering University,2017,38(5):697-704.

[14] LI C H,ZHAO Y S, WANG G F, et al. Adaptive RBF neural network control for unmanned surface vessel course tracking[C]∥IEEE International Conference on Information Science & Technology, 2016:285-290.

[15] 劉程,李鐵山,陳納新. 帶有舵機特性的船舶航向自動舵DSC-MLP設計[J]. 哈爾濱工程大學學報,2012,33(1):9-14.

LIU C,LI T S,CHEN N X. Dynamic surface control and minimal learning parameter (DSC-MLP) design of a ship’s autopilot with rudder dynamics[J]. Journal of Harbin Engineering University,2012,33(1):9-14.

[16] XU B,YU L,WANG S X,et al. Neural dynamic surface hypersonic flight control using minimal-learning-parameter technique[C]∥Proc.of the IEEE International Conference on Unmanned Aircraft Systems,2014:960-966.

[17] ZHANG G Q,ZHANG X K. Concise robust adaptive path-following control of underactuated ships using DSC and MLP[J]. IEEE Journal of Oceanic Engineering,2014,39(4):685-694.

[18] SWAROOP D,HEDRICK J K,YIP P P,et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE Trans.on Automatic Control,2000,45(10):1893-1899.

[19] CAI J,WEN C,SU H,et al. Adaptive backstepping control for a class of nonlinear systems with non-triangular structural uncertainties[J].IEEE Trans.on Automatic Control,2017,62(10): 5220-5226.

[20] DO K D,JIANG Z P,PAN J. Robust adaptive path following of underactuated ships[J]. Automatic,2004,40(6):929-944.