基于精英策略改進的混合蛙跳算法

江澤昌， 劉天羽， 吳 星， 王義東

(上海電機學院 電氣學院，上海 201306)

混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFLA)最早是由Eusuff等[1]于2003年提出的，是一種模仿自然界生物行為而產生的基于種群智能后啟發式的全局優化方法。但是，SFLA和其他智能算法一樣容易收斂到局部最優，且存在著初始種群不均勻、求解精度不高、收斂速度不夠快的缺點[2-3]。

鑒于此，研究者們對SFLA進行了大量研究。文獻[4]中通過對SFLA的改進，重新定義了青蛙的覓食機制和進化迭代公式，改善了算法的局部搜索和全局搜索能力。文獻[5]中通過對學習的策略產生初始種群，在進化過程中嵌入了差分進化，對復雜函數優化使其具有較強地求解能力。文獻[6]中通過理想的搜索策略，使最差個體青蛙向最好個體青蛙學習，且在搜索過程中引入2個加速因子，提高了搜索速度。文獻[7-8]中采用隨機分組的策略，在最差學習的過程中引入Minkowski距離，避免了算法陷入局部極小，加快了收斂速度。文獻[9]中引入柯西變異算子，使算法跳出局部最優。文獻[10]中將模糊算法和混合SFLA相結合。文獻[11-12]中引入差分算法，使SFLA跳出局部最優和避免早熟。文獻[13]中對原始算法添加了變異算子，通過模糊控制器調節變異算子的規模，動態地調整變異算子在解空間的搜索范圍、不同階段和候選解分布的演化過程。上述文獻只是對子群中最差青蛙進行了更新改進，并沒有對全局最優青蛙進行改進。

針對SFLA在后期收斂速度慢、易于陷入局部最優、且精度低等問題，本文研究了一種改進的混合SFLA。由于在局部搜索中，最差青蛙只是向最優的青蛙學習，故引用精英策略對最差青蛙的位置進行更新，使最差青蛙在向最優青蛙學習的同時，也向本子群中較好青蛙學習；引入了柯西變異算子，增大了全局搜索能力，提高了搜索效率和算法的收斂速度；針對全局最優青蛙很少有機會進化的問題，引入了Minkowski距離，使全局最優青蛙既能向局部其他青蛙方向進化，也能向局部最優青蛙進化，提高了全局最優青蛙的質量。利用5個典型函數對改進后的SFLA和SFLA進行仿真實驗，結果表明，改進后的SFLA具有較快的收斂速度，能避免早熟，且優化精度高。最后，對改進的SFLA進行了收斂性分析。

1 SFLA的基本原理

SFLA是模擬青蛙在覓食的過程中，通過群體間的相互合作與競爭相互結合，以實現群體進化的目的。本文以函數的最小值為例說明SFLA的基本步驟：設群體青蛙的種群規模為M，且在d維空間里第i個個體的坐標xi=(xi1,xi2,…,xid)(i，d∈N)，計算個體的適應值，然后按照從大到小順序排列。將整個種群劃分為S個局部子群，每個局部子群中有N只青蛙，即

M=SN

在降序排列的過程中，把排列好的個體平均分配到S個局部子群中去，在指定的局部迭代次數Ne內進行搜索，若滿足全局迭代次數maxGE，則停止此次搜索，輸出全局最優值；否則，將全部青蛙混合重新計算。

在SFLA中，若局部青蛙產生的新個體優于局部子群中的最差青蛙時，則用新個體來代替局部最差青蛙，因此，在多次替換后產生的新個體必然優于之前的最差青蛙，即在多次迭代中，會使整體中局部子群的青蛙得到進化。若局部子群中產生的新個體不優于局部子群里的最差青蛙時，就用全局最優解Xg來代替局部子群中最好青蛙Xb。其具體的最差青蛙更新策略為

2 一種改進的SFLA算法

2.1 引入精英策略改進最差青蛙

精英策略的基本思想是為了保留住最適應的個體而產生的，目標就是為了將最優解的信息傳入到下一代[14]。

在基本SFLA中，局部子群中的最差青蛙只向該子群中的最優青蛙學習，最差青蛙被限制在當前位置與子群中最優青蛙的線性區域中。本文借鑒精英策略，保留子群中的最優青蛙，以防止最優青蛙向較壞方向變異而造成群龍無首，繼而出現退化的現象。選擇每組中的最差青蛙讓其以自身為原點，以到該組中最優青蛙的距離為半徑進行360°搜索，并提高搜索速度，使最差青蛙向該子群中較好青蛙學習，且在學習過程中保證自身不退化。

2.2 引用柯西分布變異算子

SFLA在后期的搜索中，很容易陷入局部收斂的情況，為避免該情況的發生，本文引入柯西分布變異算子，使算法在后期跳出局部最優。

柯西分布是概率論與數理統計中的一類常見的分布，其中一維柯西分布的函數為[15]

(3)

式中：x為隨機變量；t為常數。

當t=1時，式(3)為標準的柯西分布函數。圖1所示為標準柯西分布概率密度函數曲線。

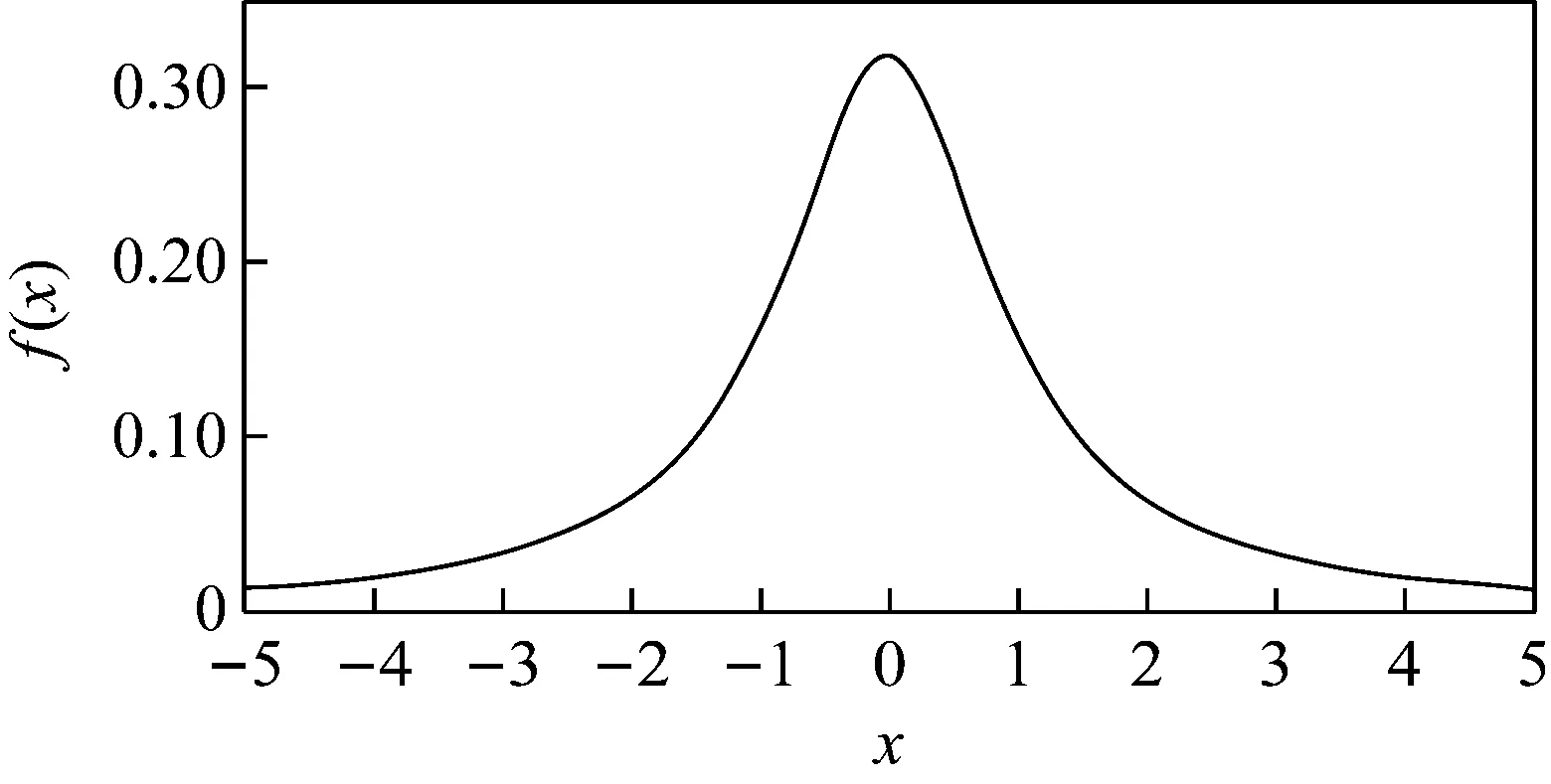
圖1 標準柯西分布概率密度函數曲線

由圖可見，曲線的兩端長扁形狀且趨于零，因此，利用柯西分布可以避免改進的SFLA在后期易陷入局部最優的情況。利用柯西分布隨機變量生成函數

η=tan[(ξ-0.5)π]

(4)

式中，ξ為[0，1]上的隨機變量。

考慮上述因素，提出了一種改進的算法，其更新策略為

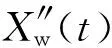
2.3 全局最優蛙改進策略

在基本SFLA中，在最差青蛙的進化過程中，全局最優的青蛙幾乎不進化。實驗證明[7]在進化過程中，全局最優地位會保持很多代，造成算法的尋優速度變慢，且容易出現早熟現象。Minkowski距離是歐氏幾何空間中的廣義距離度量，提供了豐富、靈活的度量選擇[16]。由于全局最優青蛙在位置上很少進化，為增加其進化的機會，本文利用Minkowski距離，使全局最優青蛙向局部子群中其他最優青蛙和除了最差青蛙以外的其他青蛙進行學習，以提高青蛙質量，其更新策略為

Xg=rand()c1M(Xg,Xj)+c2(Xg-Xbj)

(8)

j∈N

式中：Xj為局部除了最差青蛙以外的其他青蛙；Xbi為子群中最優青蛙；M(Xg,Xj)為Xg向其他子群除最差青娃以外學習的Minkowski距離；c1與c2為更新的權值。

改進后的SFLA算法流程圖如圖2所示。

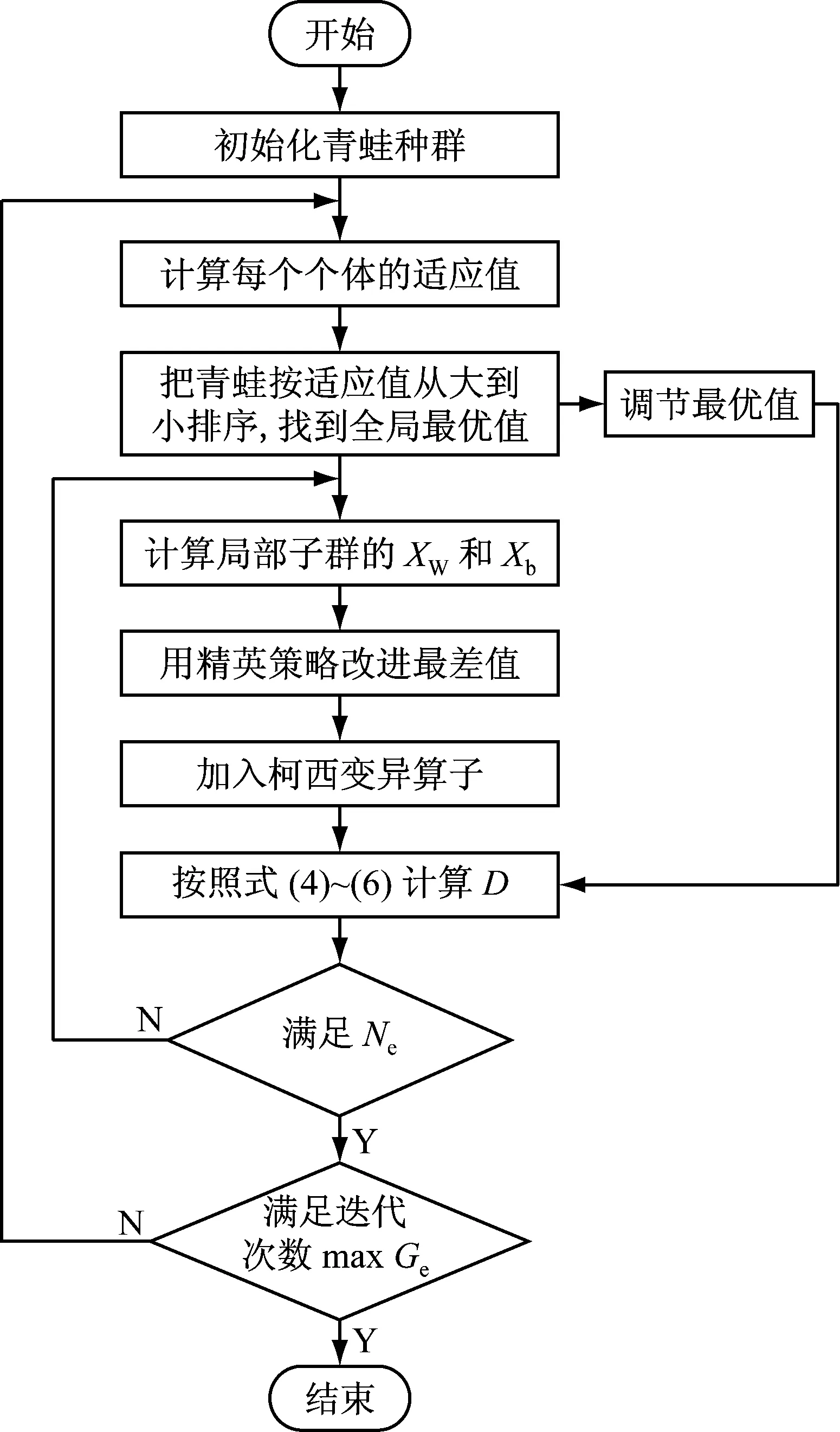
圖2 改進后的ACSFLA的算法流程圖

3 改進算法的驗證

為驗證改進策略和新算法的有效性，利用5個典型函數，即Sphere，Rosenbrook，Rastrigin，Griewank，Schaffer f7作為實驗對象，采用Matlab7.1編程，在Intel處理器5-3210M(4GB內存)中、Win7操作系統下進行了大量的實驗仿真。為增加對比性，本文所有的公共參數均設置相同，其中，M=1 800，S=30，迭代次數Ne=100。各函數的表達式和搜索范圍如表1所示。

用上述5種函數對改進后的SFLA和基本SFLA進行仿真比較，所有實驗獨立運行40次，Ne=100，表2所示為2種算法的仿真實驗結果的平均值和方差。由表2可見，改進后的SFLA對測試函數的仿真優化結果，無論是其最優解還是平均值，都較基本SFLA的要小，可見，由于引入了精英策略和Minkowski距離后，使最差青蛙的進化得到了保證，也提高了全局最優青蛙進化的機會，因此，改進后的SFLA較基本SFLA具有更好的優化效果；同時，改進后的SFLA獲得的平均值與標準差都比基本SFLA的小，說明改進后的SFLA較基本SFLA在精度上有了明顯提高。

表1 測試函數

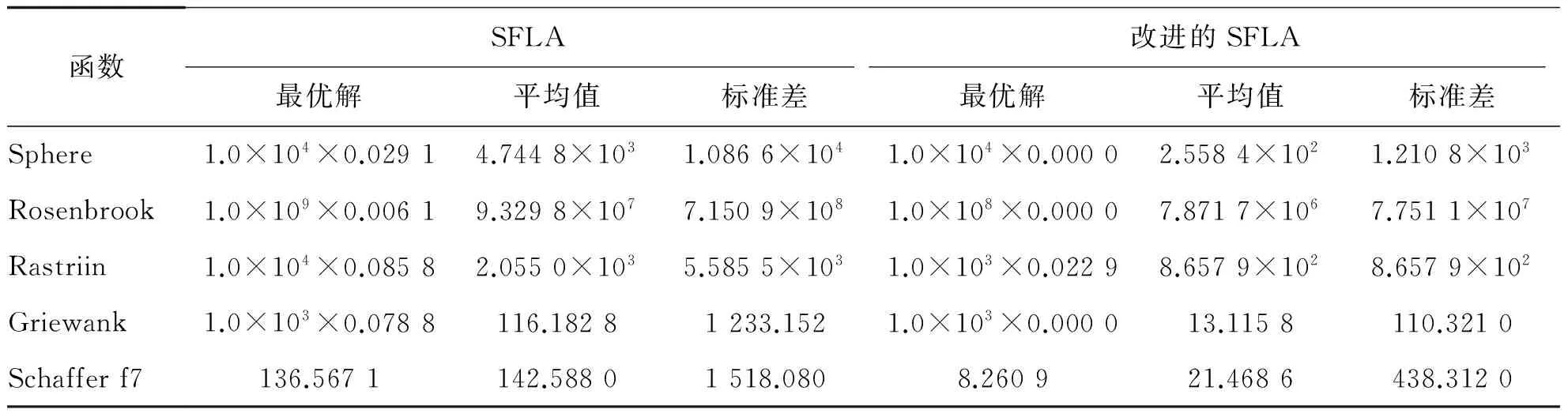
表2 2種算法對測試函數的仿真優化結果比較

由于改進后的SFLA算法較基本SFLA算法在仿真過程中存在著許多偶然因素，本文利用這2種算法對5種測試函數分別迭代100次和1 000次，運行40次后得到函數最優解的運行曲線如圖3所示。由圖可見，無論是哪種函數，改進后的SFLA較基本SFLA的收斂速度都要快，而且隨著迭代次數的增加，改進后的SFLA的收斂性得到了明顯提高，并跳出了基本SFLA局部收斂，使后期收斂速度慢的問題得到了解決。

4 改進后SFLA的收斂性分析

本文借鑒文獻[17]對SFLA收斂性的分析，對改進的SFLA進行分析，其證明過程如下。

由式(5)～(7)可得第k次迭代后，

(9)

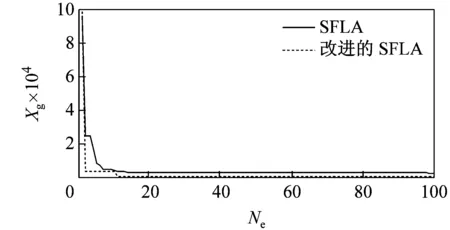
(a)Sphere函數迭代100次

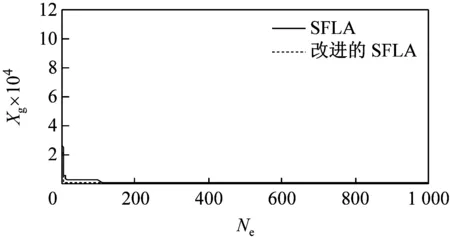
(b)Sphere函數迭代1 000次

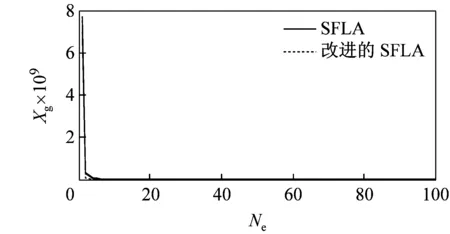
(c)Rosenbroock函數迭代100次

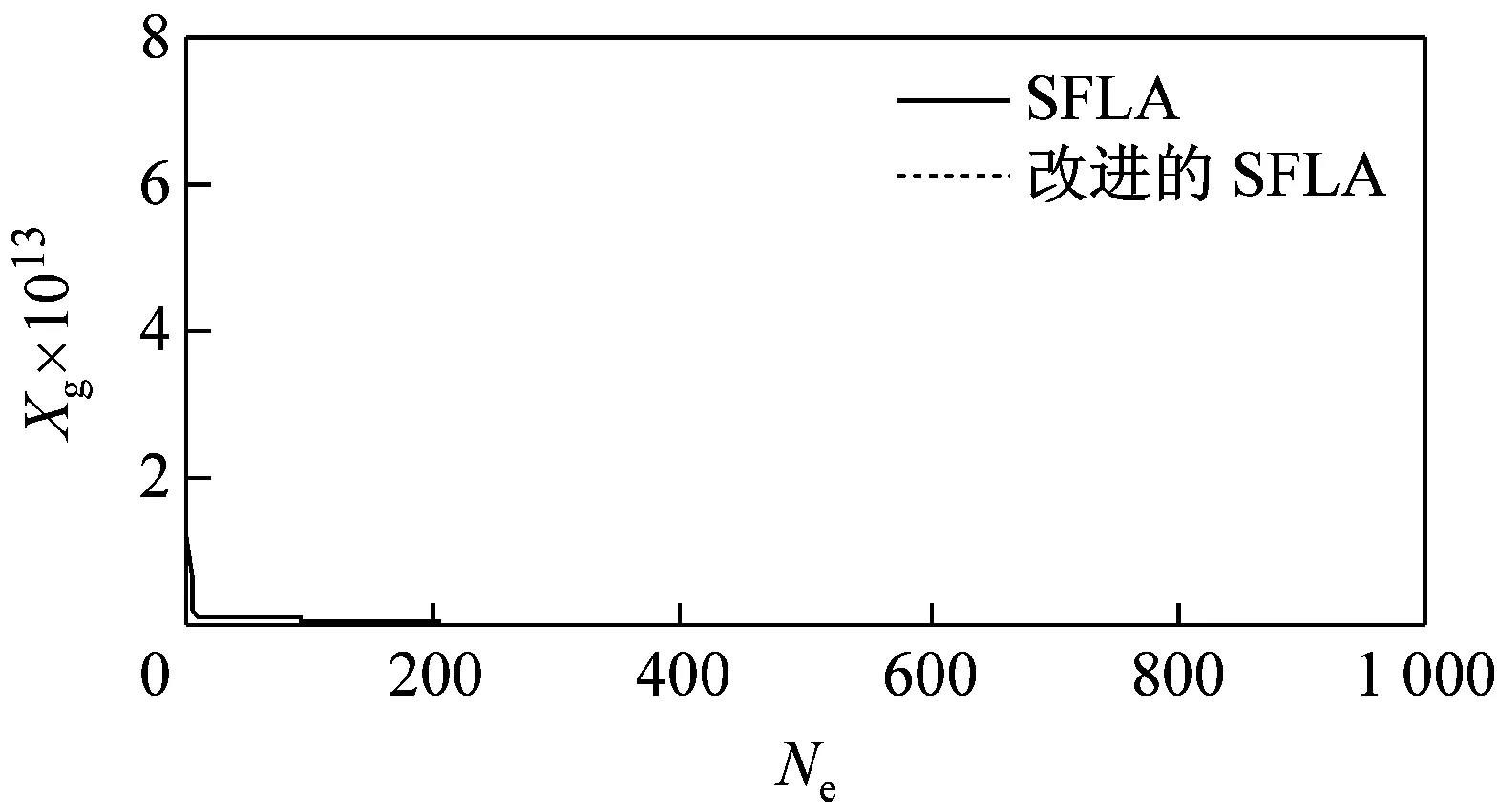
(d)Rosenbroock函數迭代1 000次

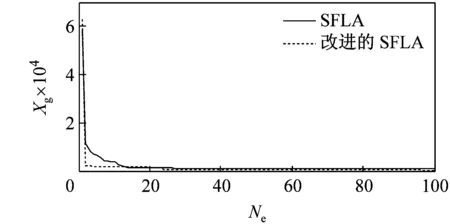
(e)Rastrin函數迭代100次

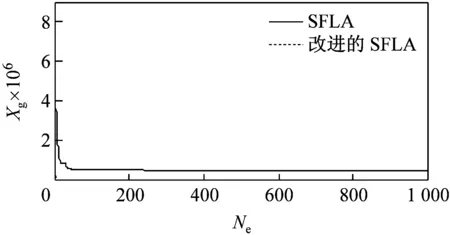
(f)Rastrin函數迭代1 000次

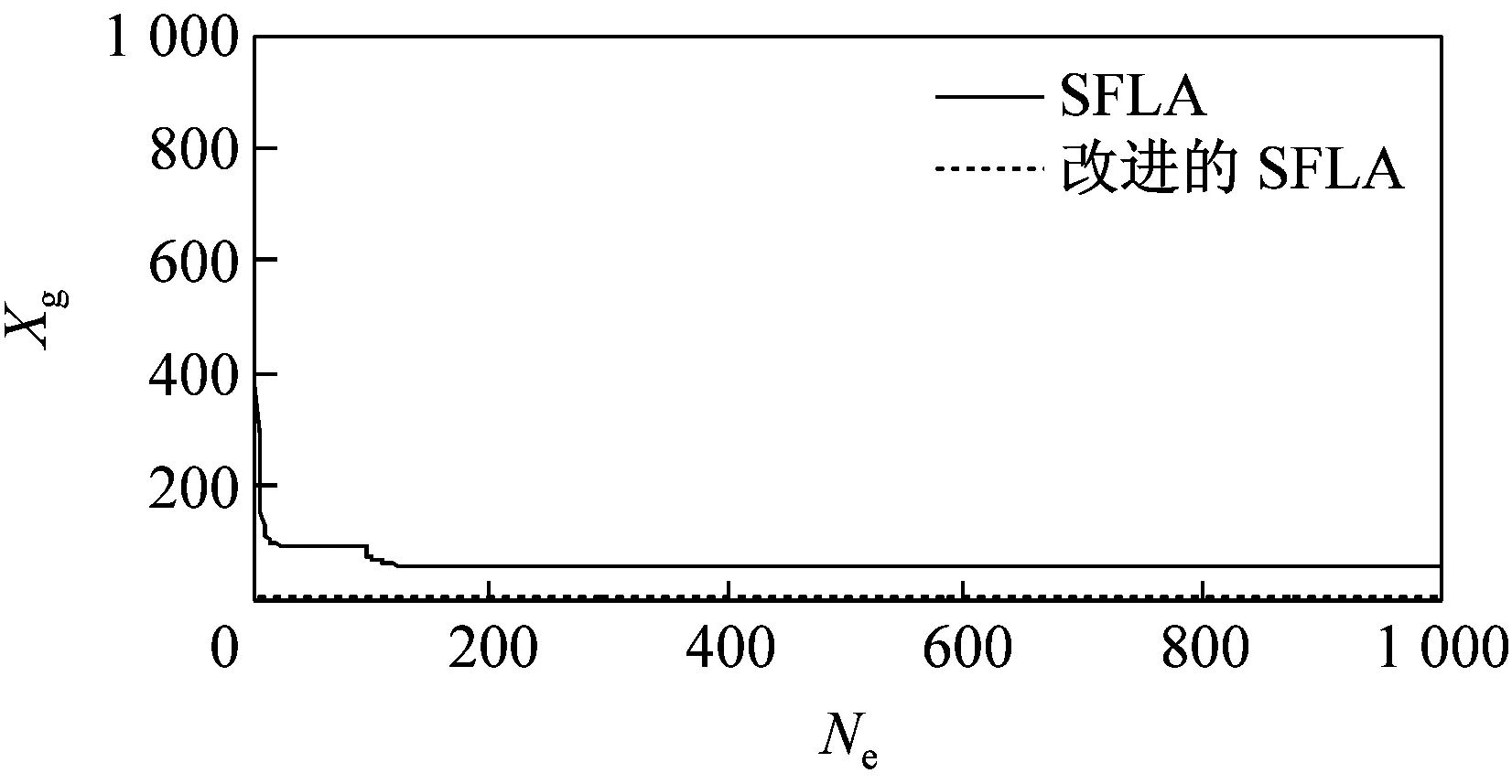
(h)Griewank函數迭代1 000次

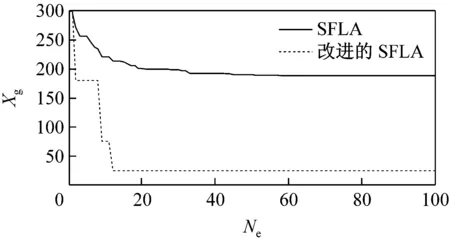
(i)Schaffer f7函數100次

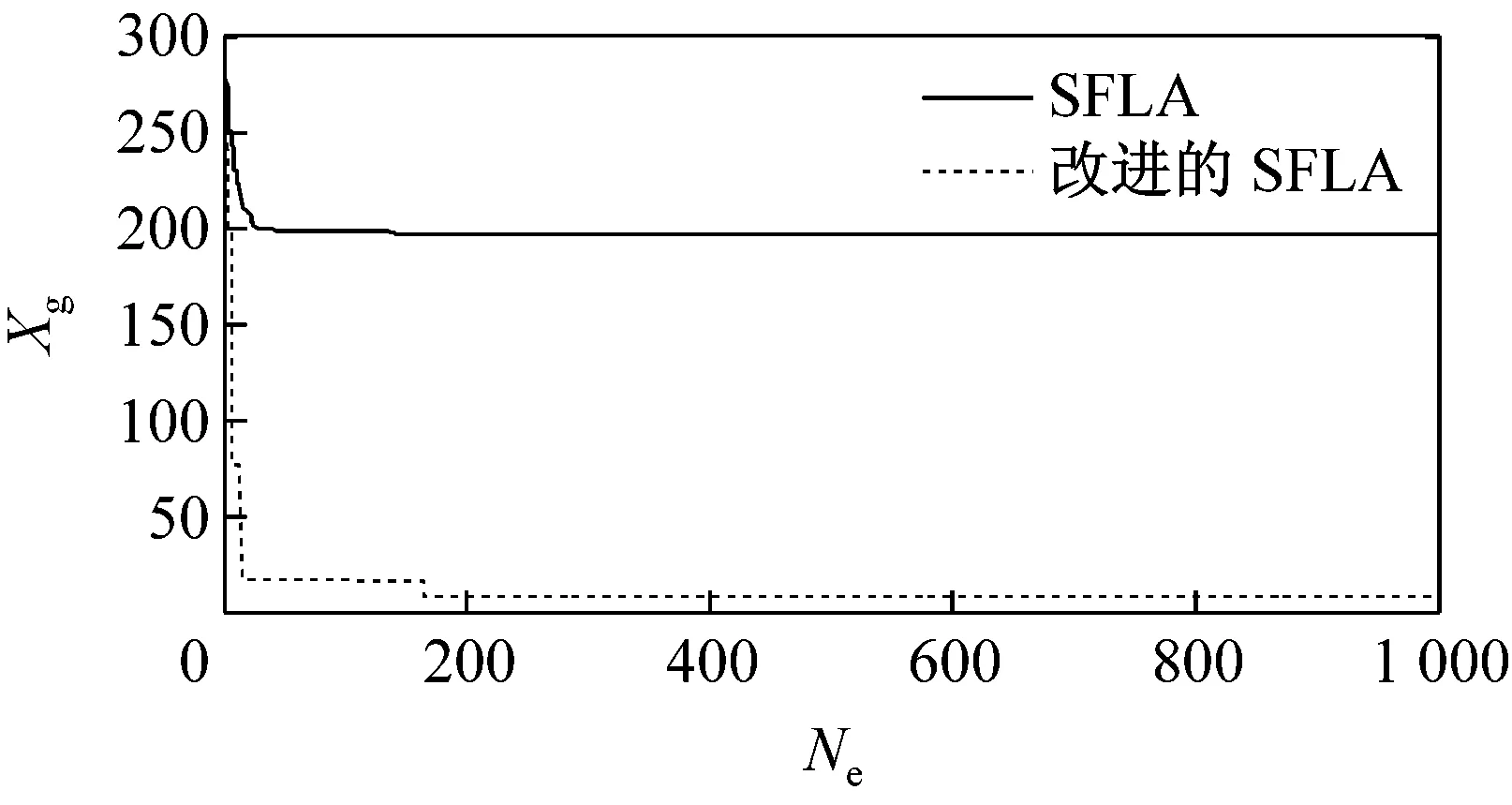
(j)Schaffer f7函數1 000次

而第k+1次迭代后，

(10)

將式(9)與(10)相減

ΔXk+1=Xk-Xk-1， Δe=(ejθ′-ejθ)

可得

(15)

分別以進化k次和k+1次的青蛙為圓心，在(0°,360°)的搜索范圍內搜索，得到它們的差值Δe，再與式(7)聯合，可得

(16)

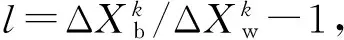
5 結 語

針對基本SFLA在后期收斂速度慢和易于陷入局部收斂的問題，研究了基于精英策略的改進SFLA，通過引入精英策略對最差青蛙進行改進，引入柯西分布變異算子改進了搜索策略，并利用Minkowsk距離提升了全局最優青蛙優化的機會；通過對常用的5個測試函數進行仿真測試，結果表明，改進的SFLA具有較快的收斂速度，能夠避免早熟，且優化精度高。最后，通過對改進的SFLA進行收斂性分析，其收斂性可以以等比數列進行分析。

[1] EUSUFF M, LANSEY K, PASHA F.Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization [J].Engineering Optimization, 2006, 38(2):129-154.

[2] 賀毅朝,曲文龍,許冀偉.一種改進的混合蛙跳算法及其收斂性分析 [J].計算機工程與應用,2011,47(22):37-40.

[3] 蘇仟.混合蛙跳算法研究與改進 [D].西安：西安電子科技大學,2014：19-20.

[4] 趙紅星,常小剛.一種改進的混合蛙跳算法 [J].蘭州交通大學學報,2017,36(1):51-56.

[5] 趙鵬軍,劉三陽.求解復雜函數優化問題的混合蛙跳算法 [J].計算機應用研究,2009,26(7):2435-2437.

[6] JABALLAH S, ROUIS K, ABDALLAH F B, et al. An improved shuffled frog leaping algorithm with a fast search strategy for optimization problems [C]//IEEE International Conference on Intelligent Computer Communication and Processing. Cluj Napoca, Romania：IEEE,2014:23-27.

[7] 魏立新,鄭翠紅,王洪慶,等.混洗蛙跳算法的改進研究 [J].控制工程,2016, 23(2):167-172.

[8] BALA S M, MEENAKUMARI R. Optimum generation scheduling using an improved adaptive shuffled frog leaping algorithm [C]//International Conference on Cognitive Computing and Information Processing.[S.l.]：IEEE,2015:1-6.

[9] 王晨.基于混合蛙跳算法的微電網運行優化 [D].蘭州：蘭州理工大學,2014:19-20.

[10] 王洋,劉志珍.基于蛙跳模糊算法的Jiles Atherton鐵心磁滯模型參數確定 [J].電工技術學報,2017,32(4):154-161.

[11] 王娜,高學軍.一種新穎的差分混合蛙跳算法 [J].計算機系統應用,2017,26(1):196-200.

[12] 何兵,車林仙,劉初升.一種蛙跳和差分進化混合算法 [J].計算機工程與應用,2011,47(18):4-8.

[13] 葛宇，王學平，梁靜. 改進的混合蛙跳算法 [J].計算機應用，2012，32(1): 234-237.

[14] 張家善,王志宏,陳應顯.一種基于精英策略的改進蟻群算法及應用 [J].計算機系統應用,2012,21(10):105-108，134.

[15] 黎紅玲,羅林,蒲冬梅,等.基于柯西分布的粒子群優化算法改進 [J].電子科技,2016,29(01):33-35，39.

[16] 盧賓賓,楊歡,孫華波,等.利用Minkowski距離逼近道路網絡距離算法研究 [J].武漢大學學報(信息科學版),2017,42(10):1373-1380.

[17] 肖瑩瑩,林廷宇,李伯虎,等. 混合蛙跳算法自適應參數調整改進策略 [J].系統工程與電子技術,2016,38(8):1939-1950.