風速前饋與模糊PID結合的變槳距控制

金鵬飛， 謝 源， 王 杰， 肖立健

(上海電機學院 電氣學院，上海 201306)

為了確保風力發電機組在額定風速以上能安全穩定運行，通常通過變槳距的方式限制風力發電機組吸收的功率，即通過改變槳距角的大小來改變風力發電機組的風能利用系數，使機組的輸出功率穩定在額定值附近[1]。針對傳統PID控制技術難以在大慣性、強耦合的風力發電機組中取得較好控制效果，國內、外學者提出將智能控制技術應用到變槳控制中[2-3]。其中，滑模控制[4]、神經網絡控制[5]、自適應控制[6]、模糊控制[7-11]等智能控制算法逐漸被應用到變槳控制中，且取得了較好地控制效果。文獻[4]中提出了一種改進的滑模變槳控制策略，采用基于支持向量機的趨近律減弱了滑模控制中的抖振，在該控制策略下，風力發電機組輸出的功率穩定且抗干擾能力較強。文獻[6]中提出了一種改進型的自適應BP神經網絡，在神經網絡反向傳播調整連接權值時，不同的連接權處采用不同的學習率進行尋優，進一步提高了系統的誤差收斂速度，控制效果較好。文獻[7-10]中提出了模糊自適應PID控制的方法，通過功率誤差及其變化率實時調整PID控制器參數的數值，提高了系統的響應特性，且輸出的功率更加平穩。文獻[11]中將模糊控制與PID控制相結合，同時利用模糊控制的魯棒性、快速性以及PID控制的精確性，當功率誤差較大時采用模糊控制，當功率誤差較小時采用PID控制，具有較好地控制效果。文獻[12]中在模糊控制與PID控制切換的過程中，運用了一種軟開關的方式，使模糊控制與PID控制平穩過渡，有效減少了控制器切換對系統產生的影響。文獻[14]中提出了一種變論域的模糊控制方法，通過變論域的方式改變模糊控制器輸入、輸出論域的范圍，在模糊控制規則數量不變的情況下，提高了模糊控制精度。文獻[15]中將轉矩誤差及其變化率作為槳距角模糊控制器的輸入，實現了轉矩和變槳控制的解耦，同時給出了一種功率平均值限制算法，可抑制陣風帶來的轉速過大和功率損失。

本文提出了一種風速前饋的模糊PID變槳控制策略，采用了一種平滑函數作為模糊控制與PID控制切換的依據。該方法在功率誤差較大時利用模糊控制的快速性提高了系統的響應，在功率誤差較小時利用PID控制器的精確性彌補了模糊控制穩定時存在靜差的問題；通過Matlab仿真表明，該方法減少了控制器切換對系統造成的影響，用風速前饋的方式實時補償槳距角度，提高了系統的響應性。

1 風力發電機組建模

1.1 風輪模型

由空氣動力學可知，風力發電機組捕獲的風能為[2-3]

(1)

式中:Pw為風力發電機組吸收的風能；ρ為空氣密度；Ar為風輪面積；λ為葉尖速比；β為槳距角；v為風速；Cp為風能利用系數，

(2)

是λ和β的函數，根據貝茲理論，其理論極限為0.593。

1.2 傳動系統建模

在永磁同步風力發電機組中，發電機轉子的轉速和風輪的轉速相同，可得到如下簡化的傳動鏈方程：

(3)

式中:Tm為風輪的機械轉矩；Te為發電機電磁轉矩；J為風力發電機組的轉動慣量。

1.3 永磁同步風力發電機建模

忽略發電機磁路飽和、渦流、磁滯損耗以及溫度環境等因素影響，假設磁場沿氣隙圓周呈正弦分布，永磁同步電動機d/q軸模型如下[3-4,7,11]：

(4)

式中:ud和uq分別為d，q軸電壓；id和iq分別為d，q軸電流；Ld和Lq分別為d，q軸電感；Rs為定子電阻；φ為永磁體磁通；ωe為轉子電角速度。

假設定子d，q軸電感相等，永磁同步風力發電機的電磁轉矩為

Te=1.5Npiqφ

(5)

式中,Np為發電機極對數。

1.4 變槳執行機構建模

目前，兆瓦級別風力發電機組大多采用液壓和電動的變槳執行機構，可將變槳執行機構的簡化為

(6)

式中:τβ為時間常數；βc為給定槳距角；β為實際槳距角。

將式(6)進行拉氏變換，可得

(7)

式中:s為復頻率。

2 控制器設計

本文研究的風速模糊前饋與模糊PID平滑切換的控制策略框圖如圖1所示。圖中，P，P*為風力發電機組實際功率和額定功率；e為功率誤差；Δv為當前時刻風速與前一時刻風速的差；β1為模糊PID控制器輸出槳距角；β2為風速前饋槳距角；β3為最終輸入到變槳執行機構的角度，為β1與β2的數值和。

圖1 系統控制結構圖

通過誤差閾值切換模糊控制器與PID控制器是常用的一種方式。當誤差大于設定的閾值時，采用模糊控制器對系統進行控制；當誤差小于設定閾值時，采用PID控制器。這種控制方式在切換點處可能會因輸出的槳距角不連續而導致系統不穩定，因此，本文采用了一種軟開關的控制方式，在模糊控制器與PID控制器切換的過程中增加一個過渡區域，并引入合適的平滑因子，使系統在模糊控制器與PID控制器切換時平穩運行；同時，通過風速前饋模糊控制器，根據測量得到的風速給出合適的前饋槳距角，對于慣性大的風力發電機組，合適的前饋槳距角可有效提高系統的響應速度。

2.1 模糊控制器

將誤差e和誤差變化率eC作為二維模糊控制器的輸入，控制量βFC為模糊控制器輸出的槳距角。e，eC和βFC的模糊子集設定為{負大(NB), 負中(NM), 負小 (NS), 零(ZO),正小(PS), 正中(PM), 正大(PB)}。根據變槳功率控制要求，功率偏差小于額定功率的10%，即±200 kW，控制量的基本論域為[-6°，6°]，故輸入量e的量化因子Ke=0.03，誤差變化率的量化因子KeC=0.015，使得控制器輸入和輸出變量的物理論域都為{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。

為保證功率輸出的平穩性，可采用平滑的高斯型隸屬函數，模糊控制規則如表1所示。

表1 模糊控制規則表

清晰化常用的方法有最大隸屬度法、中位數法和重心法3種[2]。其中，最大隸屬度法取對應輸出模糊集中隸屬度值最大的論域中的值作為輸出，當最大隸屬度對應一個或多個論域值時，取算術平均值為輸出；中位數法是從已知的模糊子集中求得對應的隸屬函數曲線，并求出隸屬函數與橫坐標圍成的面積，將所得面積除以2，該方法考慮了各點的情況，但計算較為復雜；重心法也即加權平均法，它涵蓋和利用了模糊集合的所有信息，不僅有公式可尋，且理論上較合理，故本文選用重心法來去模糊。

2.2 PID控制器

PID控制器作為最常用的控制器，具有簡單、可靠的特性。常見的PID控制器有位置式PID和增量式PID。本文采用增量式PID，控制器輸出為

(8)

式中:kP為比例系數；kI為積分系數；kD為微分系數；T為采樣周期；k為采樣序號，k=1，2，…；e(k-1)和e(k)分別為第k-1和第k時刻的偏差信號；第k和第k-1時刻控制器的輸出差值為

Δu(k)=kP[e(k)-e(k-1)]+kIe(k)+

kD[e(k)-2e(k-1)+e(k-2)]

(9)

一般情況下，PI控制器即可滿足控制要求，故式(9)可簡寫為

Δu(k)=kP[e(k)-e(k-1)]+kIe(k)

(10)

根據式(10)在Matlab/Simulink中搭建增量式PID控制模型如圖2所示。

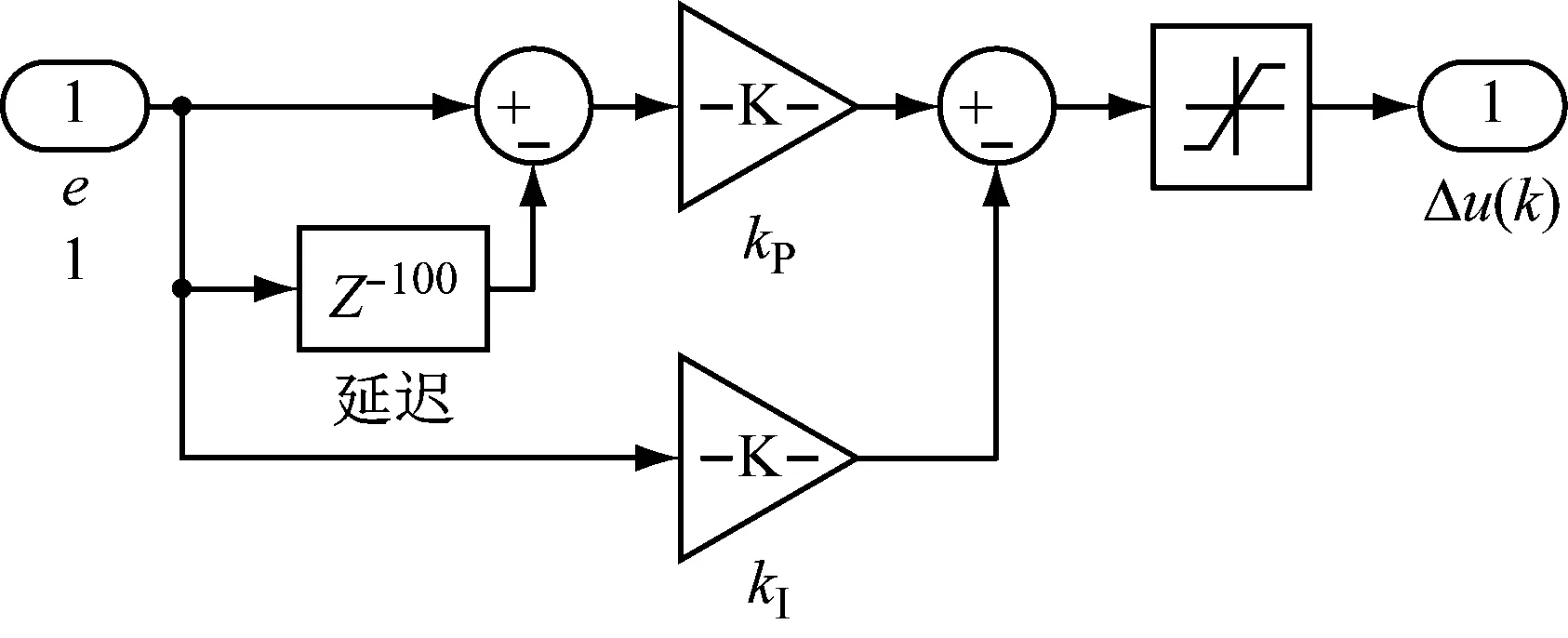
圖2 增量式PI控制結構圖

在整個系統中，采用離散的計算方式，離散時間為1 ms，故在圖2中，延時環節的延長時間為100 ms。其中，kP=22×10-7，kI=13×10-6。

2.3 平滑函數設計

模糊PID平滑切換控制器的輸出為

β1=θβFC+(1-θ)βPID

(11)

式中:β1為模糊平滑切換控制器的輸出；βPID為PID控制器的輸出；θ為平滑因子。

根據不同場合的不同需要，可選擇合適的θ，其函數模型為

(12)

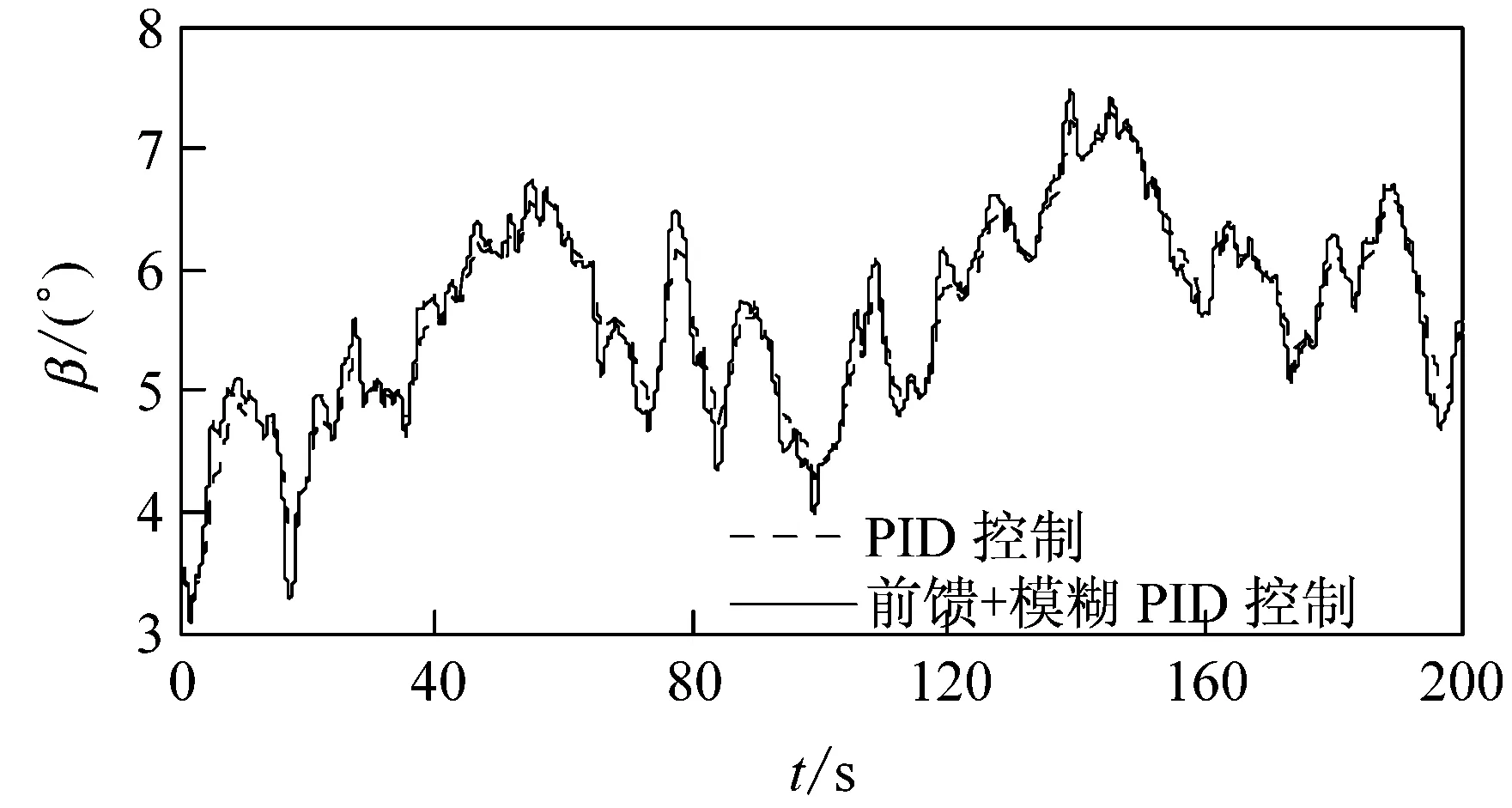
式中:x1和x2為臨界點；δ為波形系數。當|e|x1時，θ=1，模糊控制器起全部作用；當x1<|e|

圖3所示為平滑因子θ曲線圖。由圖3可見，當δ越小時，在過渡區域中，隨著e增大，θ迅速變大，模糊控制器起主要作用；當δ越大時，在過渡區域中，隨著e增大θ緩慢增大，PID控制起主要作用，當e足夠大時，模糊控制器迅速起著主要作用。

經過多次實驗后，取過渡區域為[0.35，2]，e的量化因子為2×10-4，δ=-10。e折算后，當e<0.35時，PID控制起全部作用；當e>2時，模糊控制起全部作用；當e介于0.35～2時，PID控制器和模糊控制器共同作用，且對應的平滑因子θ隨e的改變而改變。

圖3 平滑切換因子曲線圖

2.4 模糊控制器

風力發電機組是一個大慣性、非線性的系統，且變槳機構的執行需要一定時間，故采用了風速前饋方式以提高系統的響應速度。

通過機艙頂部的風速儀[11]可以測到實際風速v，然后根據不同時刻的風速v(k)給出合適的槳距角前饋值β2，并與模糊PID控制器的輸出β1相加，作為最終的槳距角輸出β3。

該前饋模糊控制器有前一時刻的風速v(k-1)和當前時刻與前一時刻風速的差值Δv2個輸入量，與前饋槳距角β21個輸出量。

風速的基本論域為[13 m/s,25 m/s]，模糊論域為{1,2,3,4,5}。對應的模糊子集有稍高(little high)、較高(relative high)、高(high)、很高(very high)、非常高(extremely high)，分別簡寫為{LH,RH,H,VH,EH}。風速的增量Δv的基本論域為[-3 m/s,3 m/s]，其對應的模糊論域為{-3,-2,-1,0,1,2,3}，模糊子集為{NB,NM,NS,ZO,PS,PM,PB}。表2所示為模糊前饋規則表。

表2 模糊前饋控制規則表

槳距角的增量變化范圍為[-4°，4°]，為達到較精確的控制效果，輸出量的模糊子集和模糊論域分別為{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}和{NB2,NB1,NM2,NM1,NS2,NS1,ZO,PS1, PS2,PM1,PM2,PB1,PB2}。模糊前饋控制器的輸入、輸出隸屬函數均采用簡單的三角隸屬函數，去模糊化方法采用重心法。

3 仿真與分析

為驗證風速前饋的模糊PID變槳控制策略的有效性，在Matlab/Simulink中搭建了2 MW永磁同步風力發電機組模型，并建立風速前饋與模糊PID控制結合的變槳控制器，將仿真結果與傳統PID變槳控制策略做了比較。2 MW永磁同步風力發電機組的具體參數如表3所示。

表3 2 MW風力發電機組參數

仿真采用風速測量儀測量實際的200 s內的風速，其風速曲線如圖4所示。

圖4 200 s風速曲線圖

將測量的200 s內的風速信號作為風力發電機組模型中的輸入，在風速前饋與模糊PID控制結合的變槳控制器與傳統的PID變槳控制器的分別控制下，風力發電機組的槳距角與功率變化如圖5所示。

(a)槳距角

(b)功率

由圖5(a)可見，當風速在額定風速以上時，風力發電機組通過風速前饋與模糊PID控制策略能夠平滑地切換模糊控制器與PID控制器，并使輸出槳距角連續；且風速前饋與模糊PID結合的變槳控制器輸出的槳距角幅度大于傳統PID變槳控制器。由圖5(b)可見，由于圖5(a)中各控制器輸出的槳距角不同，風力發電機組輸出的功率也有較大差別。風速前饋與模糊PID結合的變槳控制策略相對與傳統PID控制而言，風力發電機組輸出的功率波形幅度更小，功率更加平穩，因而具有更好的控制效果。

圖6為200 s內風速經前饋模糊控制器后輸出的槳距角補償角度變化圖，它是由測量的風速作為前饋模糊控制器的輸入，根據前一時刻的風速及風速的變化所給出的合適的前饋槳距角度。

盡管圖6中的前饋槳距角的幅值較小，但是，風輪的氣動轉矩對槳距角的靈敏性在高風速時遠大于低風速，槳距角的細微變化對風輪轉矩都會產生較大的影響[11]。將該控制器輸出的前饋槳距角作為模糊控制與PID控制結合的控制器輸出槳距角的補償角度，對于大慣性、強耦合的風力發電機組而言能提高系統的響應特性。

圖6 200 s內前饋槳距角曲線圖

4 結 語

本文提出了一種風速前饋與模糊PID結合的變槳控制策略。為維持風力發電機組輸出功率的穩定性，在功率誤差較大時采用模糊控制器，在功率誤差較小時采用PID控制器。該控制策略同時利用了模糊控制器的快速性和PID控制的精確性的特點，且在模糊控制器與PID控制器切換時采用軟開關的形式。通過采用平滑函數，依據功率誤差的大小實時調整模糊控制器與PID控制器輸出所占比重，避免了控制器直接切換造成的輸出不連續問題，有效維持了系統輸出的穩定性。同時通過測量的風速實時進行槳距角的前饋調節，可以根據風速的特性給出合適的前饋槳距角，提高系統的響應特性。

[1] 竇真蘭,程孟增,蔡旭,等. 大型風機變槳距控制系統的研究 [J]. 電機與控制應用,2011,38(3):38-44.

[2] 陳世超. 風力發電機變槳距控制技術研究 [D].北京：北方工業大學,2016:2-4.

[3] 羅佳寶. 基于模糊PID算法的風電機組變槳距控制器設計 [D].長春：長春工業大學,2015:20-21.

[4] WANG Xin, ZHU Wanli, QIN Bin，et al. Chattering free sliding mode pitch control of PMSG wind turbine [J]. IFAC Proceedings Volumes,2014, 47(3):6758-6763.

[5] SUYANTO, SOEDIBYO, FIRDAUS A A. Design and simulation of neural network predictive controller pitch-angle in permanent magnetic synchronous generator wind turbine variable pitch system [C]//2014 1st International Conference on Information Technology, Computer and Electrical Engineering. Semarang, Indonesia: IEEE, 2015:346-350.

[6] 付光杰,胡明哲. 基于改進型學習率自適應BP神經網絡的風力發電變槳距控制技術 [J].自動化與儀器儀表,2016(6):8-10.

[7] 韋徵,陳冉,陳家偉,等. 基于功率變化和模糊控制的風力發電機組變速變槳距控制 [J]. 中國電機工程學報, 2011,31(17):121-126.

[8] IBRAHIM I N, AKKAD M A A. Exploiting an intelligent fuzzy-PID system in nonlinear aircraft pitch control [C]// International Siberian Conference on Control and Communications. Moscow, Russia：IEEE, 2016:1-7.

[9] YU Huiqun, GAO Yang, ZHANG Hao. Fuzzy self-adaptive PID control of the variable speed constant frequency variable-pitch wind turbine system [C]//IEEE International Conference on System Science and Engineering.Shanghai,China: IEEE, 2014:124-127.

[10] 趙正黎，于惠鈞，張發明,等. 基于模糊PID控制的風電機組變槳距控制技術研究 [J]. 湖南工業大學學報, 2015,29(6):43-48.

[11] 郭鵬. 模糊前饋與模糊PID結合的風力發電機組變槳距控制 [J]. 中國電機工程學報, 2010, 30(8): 123-128.

[12] 牛志剛,張建民. 應用于直線電機的平滑切換模糊PID控制方法 [J]. 中國電機工程學報, 2006, 26(8): 132-136.

[13] LASHEEN A, ELSHAFEI A L. Fuzzy predictive control of the collective pitch in large wind turbines[C]//2015 European Control Conference. Linz, Austria：IEEE, 2015:1528-1533.

[14] VAN T L, NGUYEN T H, LEE D C. Advanced pitch angle control based on fuzzy logic for variable-speed wind turbine systems [J]. IEEE Transactions on Energy Conversion, 2015, 30(2):578-587.

[15] 蔣說東,劉軍. 額定風速附近變速變槳風力發電機組功率優化控制 [J]. 太陽能學報,2015,36(5):1097-1104.