考慮電網阻抗的風電變流器穩定控制方法

寧尚賢, 辛紹杰, 楊恩星, 陳慧婷

(1.上海電氣輸配電集團 技術中心， 上海 200233；2.上海電機學院 電氣學院， 上海 201306；3．遠景能源(上海)有限公司， 上海 200051)

在分布式可再生能源向電網傳輸電能的電力網絡中，由于輸電距離跨度較大，使得電力網絡中的電網阻抗成為不可忽略的因素[1-3]，導致并網逆變器與電網之間的聯系較弱，形成一種弱電網狀態[4-5]。此時，并網逆變器與電網之間形成了交互系統，使得并網逆變系統輸出的并網電能質量會受到電網阻抗變化的擾動，不利于整個系統的穩定性[6-11]。因此，研究考慮電網阻抗的風電變流器穩定控制方法對并網環節具有重要意義。

本文分析了電網阻抗變化對連續域和離散域的并網逆變控制系統的影響，研究了電網阻抗自適應的控制方法，在Matlab/Simulink環境中搭建電網阻抗自適應的并網逆變器控制系統的仿真模型，進行了仿真驗證。結果表明，該方法對維持并網逆變控制系統的穩定具有一定作用。

1 電網阻抗對三相并網逆變系統的影響

由于并網公共點與電網間的阻抗不能忽略，故并網逆變器與電網之間形成交互系統。圖1所示為考慮電網阻抗的并網逆變器控制系統模型。

圖1 考慮電網阻抗時并網逆變器控制系統模型

圖中，在并網公共點PCC處引出并網側電流反饋，UDC為并網逆變器直流側電壓;Ug為電網電壓;Gc(s)為電流控制器，為抑制LCL濾波器產生的諧振，引入電容電流有源阻尼因子kd；在考慮三相并網逆變器中開關橋臂過流保護的情況下，電容電流由逆變側電流與并網側電流相減所得[12-13]；i1為并網逆變器側輸出電流;iC為經過LCL濾波電容Cf的電流;UC為電容電壓;i2為并網側電流;Zg為與輸電網絡等效的電網阻抗;i2αref，i2βref為參考電流。

(1)

由式(1)可見，電網阻抗Zg的加入改變了理想情況下并網逆變器電流環控制系統的傳遞函數，使控制系統的穩定受到影響；同時，當忽略Zg中的電阻Rg時，只相當于改變了并網側的電感量L2。

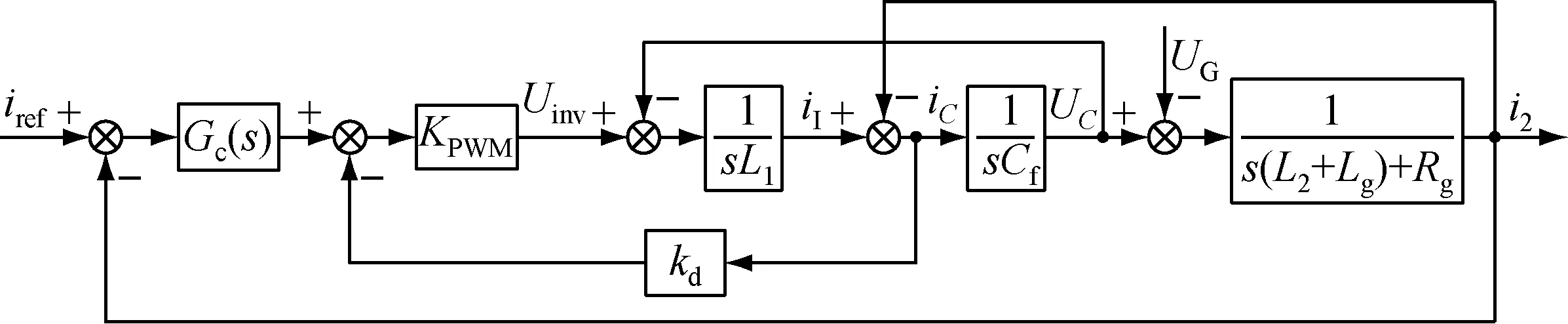
圖2 考慮電網阻抗的并網逆變控制系統電流環控制框圖

為進一步分析電網阻抗對并網控制系統的影響，圖3給出了Rg和Lg變化時的開環傳遞函數伯德圖。由圖3(a)可見，忽略Zg中的電抗后，當Rg=0 Ω時，控制系統的幅值裕度GM=13.7 dB，相角裕度PM=55.9°；當Rg=1 Ω時，GM=16.5 dB，PM=63.7°；當Rg=2 Ω時，GM=18.9 dB，PM=69.4°。可見，隨著Zg中Rg的增加，控制系統的GM和PM也隨之增加，表明并網逆變器控制系統的穩定性有一定增強。由圖3(b)可見，忽略Zg中的電阻后，當Lg=1 mH時，GM=15.1 dB，PM=33.4°；當Lg=2 mH時，GM=16.4 dB，PM=27.5°。可見，隨著Zg中Lg的增加PM降低，對控制系統的穩定性產生影響。

(a) Rg變化時

(b) Lg變化時

圖3Rg和Lg變化時的開環傳遞函數伯德圖

此外，由于并網逆變器控制系統中采用的是電容電流有源阻尼控制，故還需考慮當Zg變化時，阻尼比ζ所受到的影響，即

(2)

由式(2)可得到ζ與Zg的變化情況，如圖4所示。由圖4(a)可見，當Zg中Rg不變時，ζ隨著Lg的增加而增加；由圖4(b)可見，當Zg中Lg不變時，ζ隨著Rg的增加而減小。由此可見，Rg的存在在一定程度上抑制了ζ的增加，因此，Zg的存在不會影響電容電流有源阻尼的穩定。

(a) Rg變化時

(b) Lg變化時

2 并網逆變控制系統在離散域的穩定性分析

為進一步分析在考慮電網阻抗時復雜控制系統的穩定性，對在連續域的并網逆變器電流環傳遞函數進行離散化處理[14-15]，可得在離散域下并網逆變器電流環控制框圖，如圖5所示。

圖5 離散域并網逆變器電流環路的控制框圖

為使在連續域的電流環開環傳遞函數離散化，本文采用雙線性變換方法，可得離散域并網電流控制環路的傳遞函數為

(3)

式中：T為離散系統的采樣頻率；z為離散變化的變量。

故由式(3)和(1)可得離散域電流環傳遞函數為

(4)

式(4)所示的離散域電流環傳遞函數中沒有考慮Zg，即Rg=0，Lg=0時的離散域系統模型。由離散域的傳遞函數，可依據奈奎斯特判據進行穩定分析[16]，圖6所示為不考慮Zg時離散系統的奈奎斯特圖。

(a) 離散域下

(b) (-1,j0)點處

由圖6(a)可見，在離散域下，由于所示范圍較大，圖中觀察不到(-1,j0)點，不能確定奈奎斯特曲線與負實軸的交點是否位于(-1,j0)點的右側；故圖6(b)給出(-1,j0)點處的奈奎斯特圖。由圖可見，不考慮Zg時離散系統的奈奎斯特曲線不包圍(-1,j0)點，表明離散系統是穩定的。

而考慮Zg時，需在并網電流控制環路的傳遞函數中加入Rg,Lg分量，得到離散域電流環傳遞函數為

(5)

故得到考慮電網阻抗時離散系統的奈奎斯特圖如7所示。由圖可見，加入Zg后，離散系統的奈奎斯特曲線與負實軸的交點位于(-1,j0)的左側，且逆時針包圍了(-1,j0)點，故在考慮Zg后，離散系統的穩定性受到影響。

圖7 考慮電網阻抗時離散系統的奈奎斯特圖

3 電網阻抗自適應的控制方法設計

上述分析可知，Zg的存在使得并網逆變控制系統的穩定性受到影響。在不改變三相帶LCL濾波的并網逆變系統結構的情況下，要使系統恢復穩定，只有通過調整并網逆變控制系統中電流控制環節的控制器參數比例系數kP、諧振系數kr以及kd，才能使系統的輸出電壓、電流得到改善。

并網逆變控制系統

(6)

(7)

(8)

式中：fc為并網逆變系統截止頻率；f0為基波頻率；ω0為基波角頻率；Tf0為并網逆變系統低頻增益。

由式(6)～(8)，本文建立了自適應Zg變化的并網逆變系統結構，如圖8所示。圖中,ith為非特征諧波電流。該控制系統主要包括4個部分：Zg檢測部分；根據Zg調節控制參數部分；電流環控制環節；電容電流的前饋控制環節。

圖8 自適應電網阻抗變化的三相并網逆變控制系統結構

自適應Zg變化的控制流程如圖9所示。

圖9 自適應電網阻抗變化的并網逆變控制系統流程圖

其基本步驟如下：

(1) 在并網逆變器穩定運行后，進入Zg檢測環節，在電流基準處注入非特征諧波電流，在并網公共耦合點處，提取為并網電壓和并網電流注入非特征諧波頻率下的分量；

4 仿真驗證

基于自適應電網阻抗變化的控制方法的基本思路，在Matlab/Simulink中根據圖8搭建了自適應電網阻抗變化的并網逆變控制系統仿真模型，進行仿真實驗。

設置仿真系統參數如下：UDC=1.2 kV，Ug=690 V，f0=50 Hz，ω0=314 rad/s，Tf0=60 dB，fc=1 kHz，KPWM=600，ζ=0.7，仿真時間t=0.6 s。仿真開始時，并網逆變系統中Rg=7 Ω，Lg=25 mH；當t=0.3 s時，調整Zg，此時，Rg=5 Ω，Lg=20 mH。仿真中，設置Zg改變發生模塊的短路開關，先保持其開路狀態，當t=0.3 s時開關閉合，則電網中Rg=5 Ω，Lg=5 mH。

為驗證本文研究的自適應Zg變化的并網逆變控制系統穩定性的作用，圖10分別給出了三相帶LCL濾波的并網逆變系統在并網公共耦合點處自適應Zg變化前、后的電壓與電流的仿真波形。

(a) 自適應變化前并網電流

(b) 自適應變化后并網電流

圖10自適應Zg變化前、后的并網電壓與并網電流的仿真波形

由圖10(a)、(c)可見，在自適應Zg變化前，系統中Zg發生變化前、后輸出的并網電壓和并網電流波形均有波動產生，表明此時控制參數與電網阻抗不滿足對應關系，故并網逆變控制系統穩定性受到影響；由圖(b)、(d)可見，自適應Zg變化后，系統在Zg發生變化前、后輸出的并網電壓和并網電流波形均較為穩定，表明控制參數能夠自適應Zg變化進行調整。

圖11所示為自適應Zg變化前、后的并網電壓與并網電流的傅里葉分析結果。

(a) 自適應變化前的并網電流

(b) 自適應變化后的并網電流

(d) 自適應變化后的并網電壓

由圖可見，采用自適應控制后，并網電流和并網電壓的諧波含量有較大改善，且它們的基波幅值分別提高了0.2和1.8，總諧波失真率THD分別降低了2.03%和184.62%，表明采用自適應控制后，控制參數隨Zg的變化而改變，改善了并網電流和并網電壓中的諧波分布，其中，對并網電壓的改善更為明顯，使得并網逆變控制系統輸出的并網電壓和電網電流中的基波含量提高，減少了諧波的干擾。仿真表明，本文設計的Zg自適應控制方法對維持并網逆變控制系統的穩定具有一定的作用。

5 結 語

在考慮電網阻抗影響的情況下對風電變流器穩定控制方法進行研究，分析了電網阻抗的變化對連續域和離散域的并網逆變控制系統的影響，對復雜控制系統的穩定性做了進一步分析，從而研究了電網阻抗自適應的控制方法，建立了自適應電網阻抗變化的三相并網逆變控制系統，并在Matlab/Simulink環境中搭建仿真模型，對電網阻抗發生變化的情況進行了仿真驗證。仿真結果表明，該方法對維持并網逆變控制系統的穩定具有一定的作用。

[1] 張馨月. 弱電網條件下并網變流器控制策略的研究 [D].北京交通大學,2015:1-30.

[2] 謝少軍,季林,許津銘. 并網逆變器電網阻抗檢測技術綜述 [J].電網技術,2015,39(2):320-326.

[3] 唐婷,謝少軍,焦鑫艷. 基于電網阻抗測量的新型主動式孤島檢測法 [J].電源學報,2012(6):60-64.

[4] 華淼杰. 弱電網條件下并網逆變器控制系統的穩定性分析 [D].南京：南京航空航天大學,2014:8-31.

[5] 湯婷婷,張興,謝東，等. 基于高頻注入阻抗檢測的孤島檢測研究 [J].電力電子技術,2013,47(3):70-72.

[6] 陳新,張旸,王赟程. 基于阻抗分析法研究光伏并網逆變器與電網的動態交互影響 [J].中國電機工程學報,2014,34(27):4559-4567.

[7] KRISHNA H. Computational aspects of the bilinear transformation based algorithm for S-plane to Z-plane mapping [J]. IEEE Transactions on Automa-tic Control, 1988, 33(11): 1086-1088.

[8] GROUTAGE F, VOLFSON L, SCHNEIDER A. S-plane to Z-plane mapping using a simultaneous equation algorithm based on the bilinear transformation [J]. IEEE Transactions on Automatic Control, 1987, 32(7): 635-637.

[9] CESPEDES M, SUN Jian. Adaptive control of grid-connected inverters based on online grid impedance measurements [J].IEEE Transactions on Sustainable Energy, 2014,5(2):516-523.

[10] ARIF B, TARISCIOTTI L, ZANCHETTA P, et al. Grid parameter estimation using model predictive direct power control [J]. IEEE Transactions on Industry Applications, 2015, 51(6): 4614-4622.

[11] 王要強. LCL濾波的并網逆變系統及其適應復雜電網環境的控制策略 [D].哈爾濱：哈爾濱工業大學,2013:1-16.

[12] VESTI S, SUNTIO T, OLIVER J A, et al. Impedance-based stability and transient-performance assessment applying maximum peak criteria [J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2099-2104.

[13] 周林,張密. 大型光伏電站諧振現象分析 [J]. 電力自動化設備,2014,34(6):8-14.

[14] 楊明,周林,張東霞，等. 考慮電網阻抗影響的大型光伏電站并網穩定性分析 [J]. 電工技術學報,2013,28(9):214-223.

[15] 楊明. 大型光伏電站逆變器并網控制策略及穩定性分析 [D].重慶：重慶大學,2014:45-72.

[16] 胡壽松. 自動控制原理[M].北京:科學出版社, 2007.