毛/腈綸混紡織物在遠紅外烘箱中的干燥特性

周明星， 孟 婥， 孫以澤

(東華大學 機械工程學院， 上海 201620)

在紡織工業中，混紡比一定程度上代表了紡織品的質量，是重要的檢驗項目之一。由于化學方法的穩定性和通用性，定量化學分析是混紡纖維定量檢測應用最廣泛的一種方法。根據GB/T 2910.1—2009《紡織品 定量化學分析 第1部分：試驗通則》，混紡纖維中的1種組分由化學試劑溶解，通過計算殘留不溶組分得到各部分的比例。稱量前，不溶組分通過烘箱進行烘干，溫度為(105±3)℃，時間不少于4 h。

熱風烘干在干燥領域應用已久，常見于食品行業[1-3]和紡織行業[4-6]，例如，使用熱風烘干獼猴桃，發現指數烘干模型和無線平面薄板模型都符合烘干過程[7]。有文獻報導通過熱動力學分析，獲得了熱風烘干羊毛纖維卷筒的最優操作條件[8]；也有研究粘膠纖維卷筒烘干模型，并得到實驗驗證[9]。傳統的電熱鼓風烘干溫度控制不夠精確，本文擬采用遠紅外烘箱進行替代，通過對纖維烘干特性研究，以求提高干燥效率并應用于混紡纖維自動定量檢測系統。

與傳統電熱烘箱干燥相比，遠紅外烘箱干燥雖然都依賴干燥溫度和熱風循環對織物進行烘干，但前者采用的遠紅外加熱管加熱速度快，且烘箱溫度控制更優，對烘干效率有一定的改善。文獻[10]研究了薄荷葉在熱風烘干和遠紅外烘干下的效果，結果發現遠紅外烘干可獲得更好的效果且能量消耗更少。文獻[11]通過研究洋蔥片遠紅外烘干特性發現，水分含量影響擴散效率，而且更高的輻射強度和溫度有助于提高烘干效率。

本文首先通過試驗方法研究毛/腈綸混紡纖維在遠紅外烘箱中的干燥過程特性，探討不同的烘干條件對纖維烘干過程的影響。然后根據試驗結果建立烘干過程含水率變化的數學模型，并通過試驗驗證模型的準確性。通過對混紡纖維烘干試驗討論和模型分析，為提高纖維烘干效率提供參考。

1 試驗材料和方法

1.1 材料和設備

試驗所用材料由上海毛麻研究所提供，為送檢的混紡織物標準樣品，烘干試驗時的織物形態和盛放容器與傳統手工方法保持一致。

本文試驗使用的設備主要包括：HW-450AS型遠紅外烘箱，最高烘干溫度為300 ℃，控溫靈敏度為±1 ℃；烘箱，其內部有多個高度可供選擇放置樣品；砂芯坩堝，容量為30 mL；BAS124S-CW型電子天平，最大量程為120 g，精度為0.1 mg。

1.2 試驗方案

試驗時，將待烘干纖維放置于砂芯坩堝中，因此不同的樣品干基質量會影響水分的蒸發速度。遠紅外烘箱的加熱板位于烘箱底部，纖維離加熱板的遠近決定了纖維受到的熱輻射能量，對烘干效率有一定的影響。烘干溫度對纖維干燥效果的影響最直接，是重要的考慮因素之一。

根據上述3種因素設計了混紡纖維3因素3水平二次正交旋轉試驗，其因素水平表如表1所示。

1.3 試驗流程

1)取樣。將毛麻研究所提供的混紡織物剪切成所需質量大小的片狀樣品，然后拆分成紗線并放置于砂芯坩堝中。

2)測定干基質量。將含有紗線的砂芯坩堝放置于烘箱中烘干特定時間，然后轉移到干燥皿中冷卻并用電子天平稱量，計算得到混紡纖維干基質量。

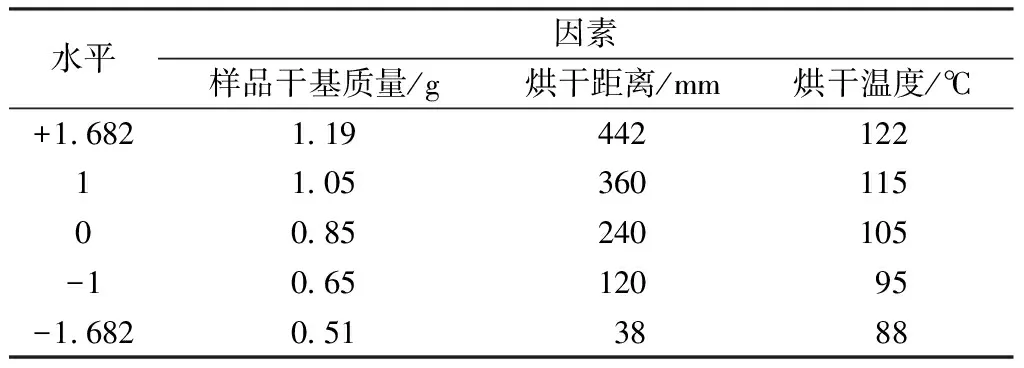
表1 遠紅外烘箱干燥試驗因素水平表Tab.1 Factor and level settings of far-infrared oven drying

3)濕樣制備。將砂芯坩堝中的樣品放置于水中浸泡0.5 h，待充分浸潤后通過微調得到固定的初始含水率。

4)樣品烘干。根據試驗方案設定初始條件，將調整后的含水樣品放入遠紅外烘箱干燥。

每組試驗同時準備多份樣品進行烘干，當烘干到特定時刻后快速拿出樣品進行稱量，并求取平均值。

2 試驗指標和結果

2.1 試驗指標

干基含水率是用來表征纖維含水量的一個重要指標，定義為纖維的實際含水量與干基質量的比值。計算公式如下：

式中：M為干基含水率；m濕為纖維含有水分時的質量，g；m干為纖維烘至質量恒定的質量，g。

干基含水率反映纖維的含水量，為體現纖維含水率隨時間的變化情況，定義纖維烘干速率如下：

式中：v為[t1,t2]時間段內的纖維平均烘干速率；Mt2為t2時刻的纖維干基含水率；Mt1為t1時刻的纖維干基含水率。

2.2 試驗結果

2.2.1樣品干基質量

為分別討論3個因素對紡織纖維烘干特性的影響，根據表1讓其中一種因素變動并固定另外2種因素在水平0處。首先分析樣品干基質量對混紡纖維遠紅外烘箱干燥過程的影響，結果如圖1所示。

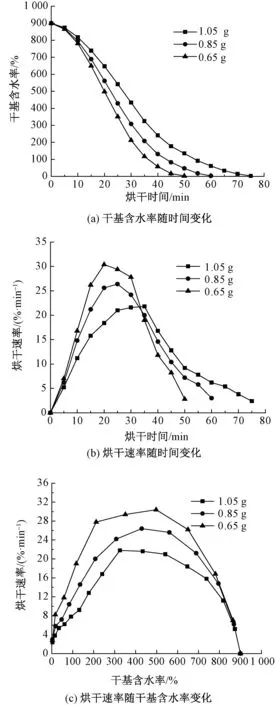
圖1 樣品不同干基質量時的纖維干燥過程Fig.1 Drying process of blends with different dry basis mass. (a) Change of dry basis moisture content with time; (b) Drying rate with change of time;(c) Change of drying rate with dry basis moisture content

由圖1(a)可知，在烘干開始階段含水率下降較慢，表明初始烘干速率相對較小。當含水率下降到600%左右時，下降速率變快，存在明顯的加速烘干過程。當干基含水率繼續下降到300%左右，烘干速率再次趨于緩慢。由圖1(b)可知，混紡纖維遠紅外烘干存在不同的速率階段，分別為加速階段、快速烘干和緩慢減速階段。圖1(c)表明，當干基含水率一致時，烘干速率隨干基質量差異明顯。

2.2.2烘干距離

遠紅外烘箱是通過加熱空氣來烘干纖維，當將烘箱內部看作溫度場時其溫度分布是不均勻的，因此，距離烘箱下部遠紅外加熱元件距離不同，纖維受到的烘干效果有差異。圖2示出不同烘干距離下的纖維干燥特性曲線。

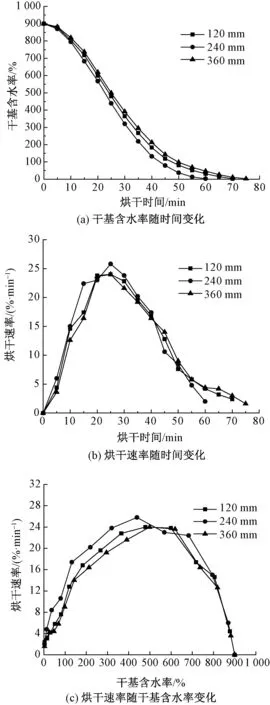
圖2 不同烘干距離時的纖維干燥過程Fig.2 Drying process of blends with different drying distances. (a) Change of dry basis moisture content with time;(b) Change of drying rate with time; (c) Change of drying rate with dry basis moisture content

由圖2(a)可知，3種烘干距離所需的烘干時間最大相差15 min左右，且干基含水率隨時間變化差異不大。需要特別注意的是，烘干距離處于中間位置即240 mm處時，獲得的烘干效果最好。這是因為離遠紅外發熱元件越近，則水汽越靠近烘箱底部，從而通過烘箱頂部排風口排出越困難；相反，離遠紅外發熱元件越遠，則纖維受到輻射的實際溫度降低，同樣不能獲得最好的烘干效果。

通過圖2(b)可知，混紡纖維的烘干仍然存在加速、快速烘干和緩慢減速過程。圖2(c)表明，當含水率一致時，烘干距離對干燥速率的影響變弱，明顯小于單樣品干基質量對烘干速率的影響。

2.2.3烘干溫度

烘干溫度決定了混紡纖維能夠受到的熱輻射能量多少，對水分蒸發速率起關鍵作用。圖3示出不同烘干溫度的纖維干燥特性曲線。

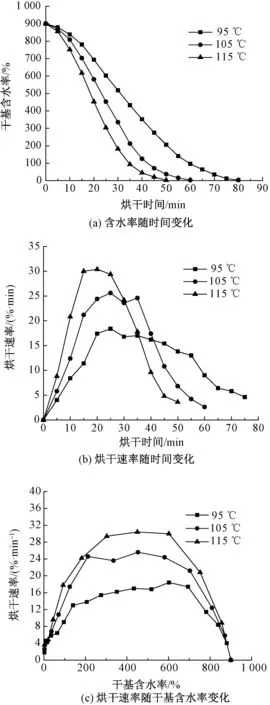
圖3 不同烘干溫度下的纖維干燥過程Fig.3 Drying process of blends at different drying temperatures. (a) Change of dry basis moisture content with time;(b) Change of drying rate with time; (c) Change of drying rate with dry basis moisture content

由圖3(a)可知，不同烘干溫度所需的最終烘干時間差異明顯，最大相差30 min。圖3(b)、(c)表明，不管是隨時間還是干基含水率變化，不同溫度下的烘干速率差異顯著。從圖3可看出，烘干溫度對烘干過程的影響是3種因素中最大的。

此外，烘干溫度為105 ℃和115 ℃之間的差異小于95 ℃和105 ℃之間的差異，說明低溫對烘干速率的降低程度更為明顯。盡管115 ℃烘干溫度可一定程度縮短纖維的烘干時間，但考慮到能源的消耗增大， 105 ℃可看成是最優的纖維干燥溫度。

3 模型建立和驗證

通過上述單因素分析，可得到混紡纖維烘干受各因素的影響情況。為進一步研究各因素之間的關系以及對纖維烘干的整體影響，需要進行烘干過程模型擬合和驗證分析。

3.1 烘干模型建立

3.1.1常見烘干模型

纖維烘干過程是復雜的非穩態傳質傳熱過程，工業烘干過程的控制常以經驗為主，盲目性較大，因此，烘干過程的數學模型模擬和分析越來越受到重視。本文研究涉及的混紡纖維烘干過程適用于薄層干燥，現選取幾種常見的干燥模型分析如下。

單項擴散模型[12]：

MR=Ae-kt

二次多項式模型[13]：

MR=a+bt+ct2

Page 模型[14]：

MR=e-ktn

式中：MR=(Mt-Me)/(M0-Me)，為任意時刻與初始狀態的水分比；t為烘干時間，min；A、k、a、b、c、n為待定系數；Mt為t時刻物料干基含水率，%；M0為物料初始干基含水率，%；Me為物料平衡干基含水率，%。為便于計算，通常將MR簡化為MR=Mt/M0，即將物料平衡時的含水率當作零。

3.1.2二次正交旋轉試驗

表2示出3因素3水平二次正交旋轉試驗得到的纖維烘干結果，將表中數據代入上述3種干燥模型進行統計學分析，得出最適合的混紡纖維干燥模型。由于不同烘干條件所需的烘干時間不同，表2所示是以烘干35 min后的剩余干基含水率為目標值。

3.1.3烘干模型擬合

將表2中的3種影響因素作為自變量，將剩余干基含水率作為因變量，采用統計學方法進行回歸擬合，結果如表3所示。可知，3種模型在0.05的置信水平下極為顯著，說明都可用來模擬纖維遠紅外烘箱干燥過程。同時，Page模型的R2均值最高，說明該模型擬合程度最好，因此，選用Page模型作為纖維遠紅外烘箱干燥動力學方程。

將Page模型線性化，得到如下形式。

ln[ln(1/MR)]=lnk+nlnt

Page模型中的待定系數k和n取決于3個試驗因素，即樣品干基質量、烘干距離和烘干溫度。考慮3個因素獨立的一次作用、二次作用及兩兩因素相關作用，將參數k和n分別用三元二次多項式擬合，得到如下回歸方程。

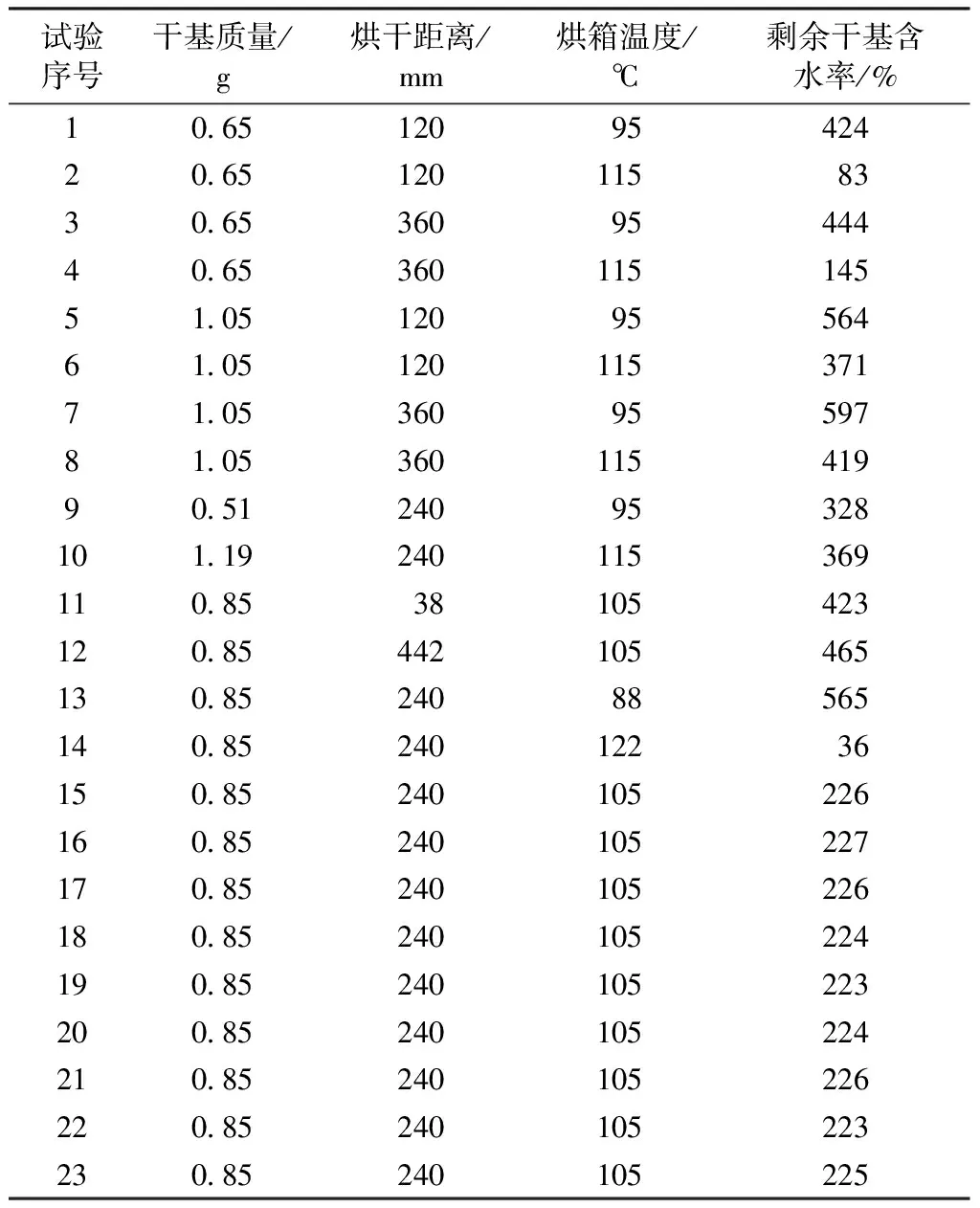
表2 遠紅外烘干二次正交旋轉試驗結果Tab.2 Results of quadratic orthogonal rotation experiment

表3 回歸方程顯著性檢驗Tab.3 Significance test of different fitting equations

式中：X1為纖維干基質量，g；X2為遠紅外輻射距離，mm；X3為烘箱溫度，℃。

3.2 烘干模型驗證

根據上述烘干模型，可預判給定條件下紡織纖維在砂芯坩堝中的烘干過程。為驗證模型的準確性，假定初始含水率為900%，纖維樣品干基質量為0.65 g，遠紅外輻射距離為240 mm，烘干溫度為105 ℃。將試驗參數代入模型，得到Mt=900e-0.002 1t2.014 7，與試驗得到的烘干數據對比，結果如圖4所示。

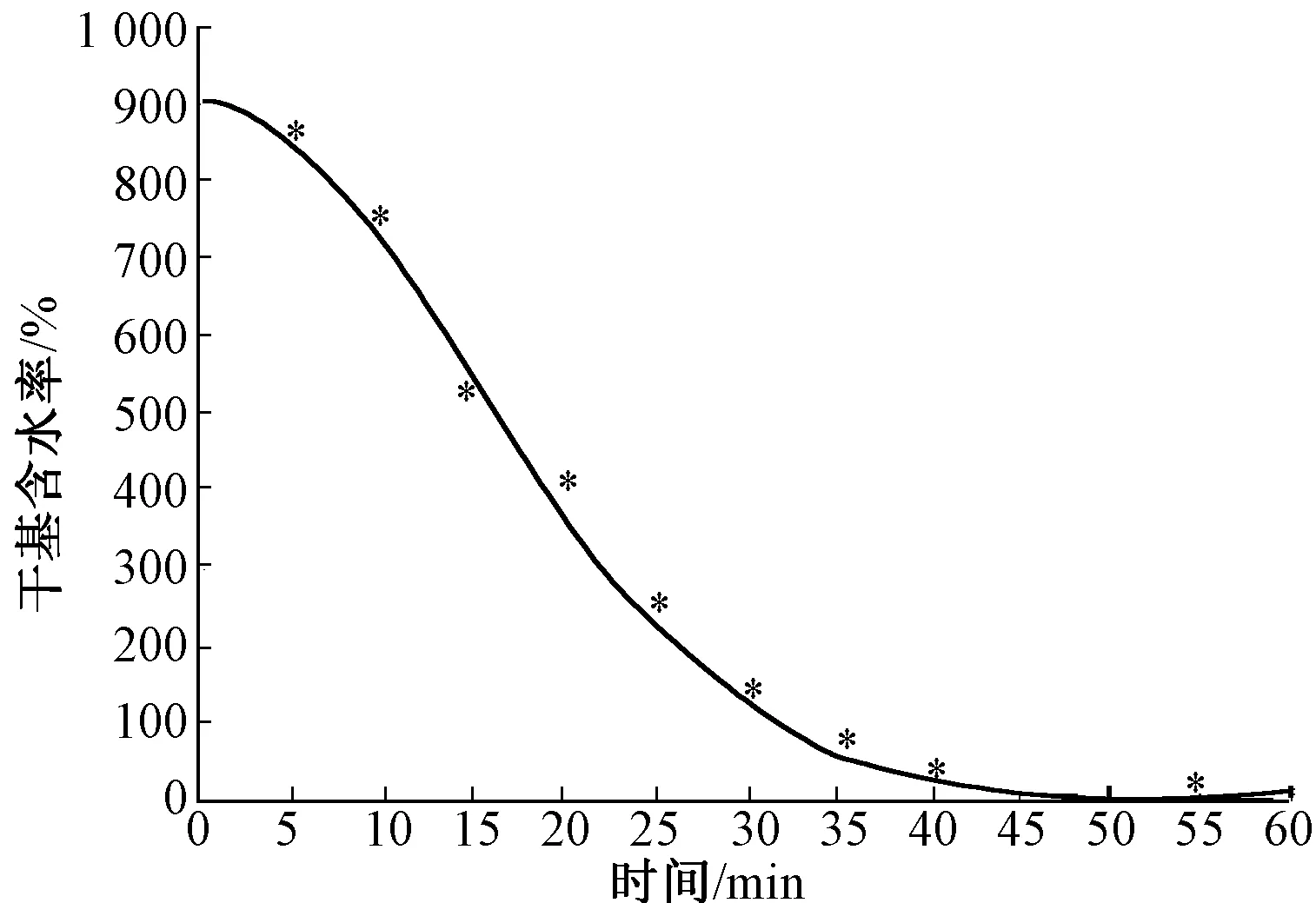
圖4 紡織纖維遠紅外烘箱干燥理論與試驗對比Fig.4 Comparison between Page model and experimental results

圖4中曲線為理論干基含水率隨時間的變化情況，點狀數據為通過試驗得到的固定時刻的纖維干基含水率。由圖可知，理論模型與試驗數據比較接近，證明模型應用得當。為客觀分析2組數據，表4示出試驗值與理論數據的誤差情況。

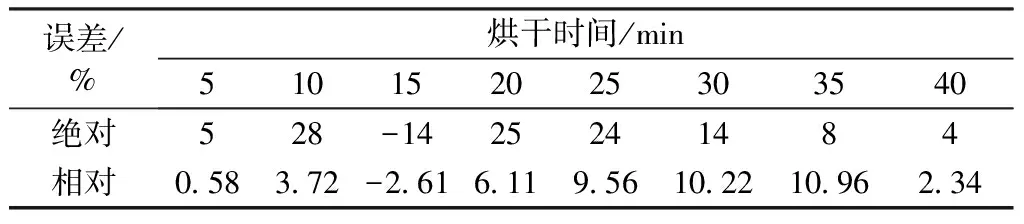
表4 理論值與試驗數據之間的誤差Tab.4 Error between model and experimental data

表4中絕對誤差代表理論值與試驗得到的纖維含水率差值，其中絕對誤差最大為28%，最小為4%。因為烘干前期纖維含水率較高，存在絕對誤差較大的可能，而烘干后期纖維含水率低且趨于穩定，絕對誤差逐漸降低；此外由表4可知，相對誤差最大為10.96%，最小為0.58%。因為相對誤差為絕對誤差除以此刻的纖維含水率，纖維含水率的遞減性導致相對誤差與絕對誤差的變化趨勢不一致。上述試驗結果和誤差分析證明，Page模型適宜作為混紡纖維放置于砂芯坩堝進行遠紅外烘箱干燥的預測模型。

4 結 論

對于混紡纖維遠紅外烘箱干燥試驗，烘干距離處于中間位置所需時間最短，且烘干溫度為105 ℃最合適。對于不同的樣品干基質量，烘干時間差異較大。不管烘干條件如何，烘干試驗存在明顯的升速、快速烘干過程和緩慢降速3個過程。通過二次正交旋轉試驗并對比3種常見的烘干模型，得到Page模型最適合于纖維遠紅外烘干，并通過數據擬合得到模型參數。將理論模型與試驗結果對比并進行誤差分析，驗證了模型的準確性。

此外，研究結果表明，采用遠紅外烘箱干燥混紡纖維所需時間隨著試驗條件不同而變化。對于實現傳統手工方法機械化的混紡纖維自動定量化學檢測系統，本文研究對提高系統工作效率有積極的促進作用。

[1] ATARES L, CHIRALT A, GONZALEZ-MARTINEZ C. Effect of the impregnated solute on air drying and rehydration of apple slices [J]. Journal of Food Engineering, 2009, 91(2):305-310.

[2] CHANG C H, LIN H Y, CHANG C Y, et al. Comparisons on the antioxidant properties of fresh, freeze-dried and hot-air-dried tomatoes [J]. Journal of Food Engineering, 2006, 77(3):478-485.

[3] HU Q G, ZHANG M, MUJUMDAR A S. Drying of edamames by hot air and vacuum microwave combin-ation [J]. Journal of Food Engineering, 2006, 77(4):977-982.

[4] AKYOL U, CIHAN A, SHALIYEV R. Thermophysical parameter estimation of a wool bobbin during convective drying process [J]. Inverse Problems in Science and Engineering, 2010, 18(2): 227-240.

[5] FOHR J P, COUTON D, TREGUIER G. Dynamic heat and water transfer through layered fabrics [J]. Textile Research Journal, 2002, 72(1): 1-12.

[6] CAY A, TARAKCIOGLU I, HEPBASLI A. Exergetic analysis of textile convective drying with stenters by subsystem models: part 2: parametric study on exergy analysis [J]. Drying Technology, 2010, 28(2):1368-1376.

[7] ORIKASA T, WU L, SHIINA T, et al. Drying characteristics of kiwifruit drying hot air drying [J]. Journal of Food Engineering, 2008, 85(2): 303-308.

[8] AKYOL U, AKAN A E, DURAK A. Simulation and thermodynamic analysis of a hot air textile drying process [J]. The Journal of the Textile Institute, 2015, 106(3): 260-274.

[9] AKYOL U, KAHVECI K, CIHAN A. Determination of optimum operating conditions and simulation of drying in a textile drying process [J]. The Journal of the Textile Institute, 2013, 104(2):170-177.

[10] NOZAD M, KHOJASTEHPOUR M, TABASIZADEH M, et al. Characterization of hot-air drying and infrared drying of spearmint(Mentha spicata L.) leaves [J]. Journal of Food Measurement and Characterization, 2006, 10(3): 466-473.

[11] PATHARE P B, SHARMA G P. Effective moisture diffusivity of onion slices undergoing infrared convective drying [J]. Biosystems Engineering, 2006, 93(3): 285-291.

[12] 王寶和. 干燥動力學研究綜述[J]. 干燥技術與設備,2009, 7(1):51-56.

WANG Baohe. Review of drying kinetics [J]. Drying Technology & Equipment, 2009, 7(1):51-56.

[13] KUCUK H, MIDILLI A, KILIC A, et al. A review on thin-layer drying-curve equations[J]. Drying Technology, 2014, 32(7): 757-773.

[14] JAIN D, PATHARE P B. Study the drying kinetics of open sun drying of fish [J]. Journal of Food Engineering, 2007, 78(4): 1315-1319.