灰色優(yōu)選模型在高速公路路線優(yōu)化的應(yīng)用

李明澤

摘要：高速公路路線設(shè)計的目標是保證線形指標的連續(xù)性，提供安全順暢的行駛條件，使路線與地形和環(huán)境相協(xié)調(diào)。在長期的工程實踐中，設(shè)計人員為了優(yōu)化路線方案，提出了很多先進的理論和方法，并應(yīng)用于工程設(shè)計中，灰色優(yōu)選模型就是其中之一。本文通過介紹灰色優(yōu)選模型的原理，結(jié)合設(shè)計實例，探討了多因素影響下路線方案比選的思路。

Abstract： The goal of expressway route design is to ensure the continuity of linear indicators， provide safe and smooth driving conditions and coordinate the route and topography and environment. In the long-term engineering practice， the designers put forward many advanced theories and methods in order to optimize the route plan， and applied them to engineering design. Gray optimization model is one of them. In this paper， by introducing the principle of gray optimization model and combining with the design examples， the idea of route selection and comparison under the influence of multiple factors is discussed.

關(guān)鍵詞：高速公路；路線設(shè)計；灰色優(yōu)選模型

Key words： expressway；route design；gray optimization model

中圖分類號：U212 文獻標識碼：A 文章編號：1006-4311（2018）08-0058-03

0 引言

高速公路的規(guī)劃和修建，影響著路網(wǎng)輻射區(qū)域的規(guī)劃與建設(shè)、資源利用和產(chǎn)業(yè)布局，尤其對地區(qū)之間的溝通產(chǎn)生巨大作用。高速公路的路線走向不僅與技術(shù)因素有關(guān)，而且受到地質(zhì)地貌、經(jīng)濟指標、人文環(huán)境等因素的影響，因此，在眾多控制因素下如何選擇合理、經(jīng)濟的路線方案成為了高速公路設(shè)計的關(guān)鍵。

路線方案比選的核心在于建立統(tǒng)一標準來評價不同影響因素，進而明確方案的優(yōu)劣排序，從中得到最優(yōu)方案。本文應(yīng)用的灰色優(yōu)選模型是一種改進的灰色關(guān)聯(lián)分析方法（以下簡稱“GRAP法”），其運用層次分析法（以下簡稱“AHP法”）進行簡化分析與計算，可以針對高速公路所經(jīng)過地區(qū)的經(jīng)濟情況、地形環(huán)境、技術(shù)指標等因素，建立高速公路路線評價模型，提供定量的分析數(shù)據(jù)和結(jié)果，從而為確定最優(yōu)路線設(shè)計方案提供科學(xué)決策的依據(jù)。

1 灰色優(yōu)選模型

灰色系統(tǒng)（GreySystem）一般指現(xiàn)實世界中信息不明確的系統(tǒng)，這類系統(tǒng)包含已知和未知的諸多信息，無法對其做出直接的預(yù)測、判斷和決策。灰色模型GM（GreyModel）理論便是針對信息不完全確知的系統(tǒng)，用微分方程來建立系統(tǒng)中已知和未知信息的關(guān)系，用微分擬合建立的模型解決灰色系統(tǒng)的問題。

改進的灰色優(yōu)選模型的基本思路：第一，構(gòu)建系統(tǒng)化、層次化的評價指標結(jié)構(gòu)關(guān)系圖（AHP法），即：計算得到各個評價指標的權(quán)重因子；第二，分析和處理各個時間序列或空間序列（GRAP法），分別計算各子序列對母序列的灰色關(guān)聯(lián)度，比較灰關(guān)聯(lián)度大小而得到目標序列[1]。

1.1 GRAP法

灰色關(guān)聯(lián)分析的實質(zhì)是分析灰色系統(tǒng)中各個子序列與母序列的關(guān)聯(lián)程度，關(guān)聯(lián)程度越大，則該子序列越接近母序列，在幾何關(guān)系上則反映為該子序列曲線的幾何形狀越接近母序列曲線的幾何形狀[2]。

1.1.1 多目標比選方案

影響路線方案的有經(jīng)濟、技術(shù)、環(huán)境等多個因素，即有m個目標，V={V1，V2，…，Vm}，各目標的權(quán)重為ωj，滿足：0？燮ωj？燮1，且 ωj=1。在路線設(shè)計中，通常具有多個設(shè)計方案，這些不同設(shè)計方案構(gòu)成決策集合：P={P1，P2，…，Pn}。方案Pj對目標Vj的屬性記為Uij（i=1，2，…，n；j=1，2，…，m），由此形成決策矩陣：

U=（uij）n×m=u11 u12 … u1mu21 u22 … u2m… … … …un1 un2 … unm。

1.1.2 確定理想方案

在決策矩陣中，不同目標的的物理意義和量綱是不一樣的，不能直接進行比較，因此需要對決策矩陣進行規(guī)范化處理。矩陣的規(guī)范化原理是采用均值化算子對原始數(shù)據(jù)進行處理，建立原始數(shù)據(jù)與均值化算子的對應(yīng)關(guān)系，得到新的矩陣，即規(guī)范化矩陣：

X=（xij）n×m=x11 x12 … x1mx21 x22 … x2m… … … …xn1 xn2 … xnm，式中xij=

由規(guī)范化矩陣求理想方案時，一般定義x0=（x01，x02，…，x0m）為理想方案，需滿足：當j目標效果值越大越好時，xoj= {xij}；當j目標效果值越小越好時，xoj= {xij}。

1.1.3 計算灰關(guān)聯(lián)系數(shù)

各個方案xi與理想方案x0的灰關(guān)聯(lián)系數(shù)為：endprint

1.1.4 計算出各個方案的優(yōu)劣排序

當不考慮各指標權(quán)重時，灰關(guān)聯(lián)度為：

當考慮各指標權(quán)重時，灰關(guān)聯(lián)度為：

1.2 AHP法

1.2.1 建立層次結(jié)構(gòu)模型

將決策的目標、考慮的因素（決策準則）和決策對象按它們之間的相互關(guān)系分為最高層、中間層和最低層，繪出層次結(jié)構(gòu)圖。

1.2.2 構(gòu)造成對比較矩陣

設(shè)某層有n個因素，X={x1，x2，…，xn}，對兩兩因素進行比較，比較時取1-9尺度，其含義見表1。用aij表示第i個因素相對于第j個因素的比較結(jié)果，則aij=1/aji，建立成對比較矩陣A：

1.2.3 成對比較矩陣一致性檢驗

①計算一致性指標CI

其中n為A的對角線元素之和，也為A的特征根之和。

②查找相應(yīng)的平均隨機一致性指標RI。對n=1，2，3，…，12，對應(yīng)的RI的值分別為0，0，0.52，0.89，1.12，1.26，1.36，

1.41，1.46，1.49，1.52，1.54。

③計算一致性比例CR

當CR<0.10時，認為判斷矩陣的一致性是可以接受的，否則應(yīng)對判斷矩陣作適當修正。

2 路線方案比選優(yōu)化的實例

西南某擬建高速公路穿越一旅游區(qū)，由于路線無法避繞，因此需要對穿越景區(qū)的局部路線進行優(yōu)化，以減少新建高速公路對景區(qū)的干擾。在方案研究階段，一共提出三個方案穿越景區(qū)，每個方案各有優(yōu)缺點，綜合比較情況見表2。

下面以此工程項目為例，運用灰色優(yōu)選模型比選三個方案的優(yōu)劣。

①首先根據(jù)表2中數(shù)據(jù)得到?jīng)Q策矩陣U：

U=29533 3.600 799618 578314 31692 89692 954.9 208 4 461.60033905 3.585 718143 971704 38866 87439 1379 153 3 466.26129212 3.545 613359 727833 30847 87395 930.0 260 3 469.203

②對U進行規(guī)范化處理后，得到理想方案：

P0=[0.946 0.991 0.863 0.762 0.913 0.991 0.855 0.739 0.900 0.991]（7）

③計算各個方案xi與理想最優(yōu)方案x0的灰關(guān)聯(lián)系數(shù)得到灰關(guān)聯(lián)系數(shù)矩陣γ：

γ=0.961 0.944 0.497 1.000 0.912 0.909 0.919 0.494 0.463 1.0000.630 0.959 0.637 0.333 0.522 0.998 0.386 1.000 1.000 0.9631.000 1.000 1.000 0.568 1.000 1.000 1.000 0.334 1.000 0.941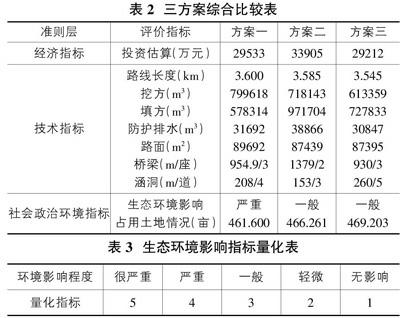

④本方案共有10個指標，由層次分析法給出各指標的相對權(quán)重，見表4。

⑤根據(jù)指標權(quán)重關(guān)系，建立成對比較矩陣，并檢驗其一致性：

一致性比例C.R.為0.00874，小于0.1，滿足一致性檢驗要求。因此，各指標權(quán)重如下：

ω=[0.087 0.043 0.043 0.043 0.043 0.043 0.087 0.087 0.348 0.176]T

⑥計算各個方案與理想方案的灰關(guān)聯(lián)度：

γ（P0，P3）=γω=0.72690.84120.9131

通過計算可以得到：三個方案與理想方案的灰關(guān)聯(lián)度分別為0.7269、0.8412、0.9131，方案三與理想方案的灰關(guān)聯(lián)度最大，所以本次設(shè)計的方案三為最優(yōu)方案。

3 結(jié)語

本文應(yīng)用灰色優(yōu)選模型，通過計算分析得到了最優(yōu)的路線方案，該方案得到設(shè)計人員和評審專家的一致認可，說明了該方法的可行性和實用性，值得推廣和研究。本文在使用灰色優(yōu)選模型時，對相關(guān)因素進行了單層次下的分析和排序，未涉及到多層次的分析計算，有一些不足之處，有待進一步探討。

參考文獻：

[1]劉思峰.灰色系統(tǒng)理論及其應(yīng)用[M].北京：科學(xué)出版社，2010.

[2]董肇君.系統(tǒng)工程與運籌學(xué)[M].北京：國防工業(yè)出版社，2007.

[3]吳小萍，陳秀方.線路方案灰色優(yōu)選模型及其應(yīng)用研究[J].北京：系統(tǒng)工程理論與實踐，2002（7）：101-105.endprint