面向非完全序列的水下三維傳感網定位算法

車 迪，牛 強

(中國礦業大學 計算機科學與技術學院，江蘇 徐州 221116)(*通信作者電子郵箱chedi@cumt.edu.cn)

0 引言

隨著無線傳感器網絡(Wireless Sensor Network, WSN)[1]應用的日益廣泛，近年來，對于無線傳感器網絡在水下應用的研究成為了熱點。水下傳感器網絡[2]是一種包括聲、磁場、靜電場等的物理網絡，其在污染預測、海洋監測、遠洋開采以及海洋數據采集等方面取得了廣泛的應用，更將在未來的海軍作戰中發揮重要的作用與優勢。在基于無線傳感器網絡的監測應用中缺乏位置信息的數據往往沒有意義，因此獲取傳感器節點的位置信息至關重要，對于水下傳感器網絡也是一樣的，得到傳感器節點的位置信息是其研究工作的重中之重。作為水下傳感器網絡的關鍵基礎支撐技術之一，節點定位技術的研究具有極其重要的理論與實際意義[3]。

現有的無線傳感網節點定位方法大多以二維空間為背景，但由于水下傳感器網絡的節點定位為三維空間模型，因此，本文以水下三維傳感網的目標定位為著眼點。另外，絕大多數基于序列的定位算法皆以信標節點通信范圍全網覆蓋為研究前提，則未知節點可接收全網信標節點的通信信息，因此該種算法皆利用全序列(序列長度為信標節點數)進行節點定位，但水下傳感網中，存在環境惡劣、信號傳播困難以及定位空間較廣等因素，所以信標節點通信范圍無法達到全網覆蓋，導致未知節點接收信標節點通信信息部分缺失。為解決上述問題，本文提出一種基于非完全序列(序列長度小于信標節點數)的水下三維傳感網定位算法。該算法利用Voronoi圖的三維空間劃分方法和階次序列定位的思想，通過虛擬信標節點、非完全序列的引入以及最鄰近序列表的加權平均估算，在保證定位精度較高的前提下有效降低了算法的計算復雜度，且未帶來額外的節點能量消耗以及網絡成本。

1 相關工作

與其他環境下的傳感器網絡相同，根據定位過程中是否實際測量節點的物理距離或方位角度，水下傳感器網絡的節點定位算法主要分為兩大類：

1)基于測距的定位算法。基于測距的定位機制通過測量相鄰節點間的實際距離或方位角度來估算未知節點的位置。一般情況下，未知節點需與信標節點進行直接通信，并利用其接收到的信號強度、到達角度或到達時間差進行測距，然后再根據其與信標節點的幾何關系來測算未知節點的坐標。在基于測距的定位算法中，最典型的幾種測距方法為：基于接收的信號強度指示(Received Signal Strength Indication， RSSI)[4]、到達角度(Angle Of Arrival， AOA)[5]、到達時間(Time Of Arrival， TOA)[6]和到達時間差(Time Difference Of Arrival， TDOA)[7]等。

2)距離無關的定位算法。距離無關的定位算法不需要節點間的絕對測距或是角度信息，僅利用節點之間的相鄰關系，依據網絡的連通度以及信標節點信息進行未知節點的位置測算。目前已提出的距離無關定位算法有：質心算法[8]、近似三角形內點測試法(Approximate Point-In-triangulation Test， APIT)[9]和DV-Hop算法[10]等。

基于序列的定位算法是近幾年提出的一種綜合基于測距和距離無關的定位算法，其核心思想是將一個二維定位平面用已排好的信標節點通過某種方式進行空間劃分，構建虛擬信標節點，并根據其與信標節點的距離次序來確定虛擬信標節點的階次序列，即定位序列。文獻[11]首次提出了WSN中基于序列的節點定位方法，利用每兩個參考點之間的垂直平分線將具有n個參考點的二維空間劃分為O(nn)個區域，并分別用序列獨一無二地表示各個區域(由于幾何約束，得到的序列實際數為O(n4))，該算法對由于無線信道的多徑干擾和遮蔽效應產生的隨機誤差具有魯棒性。文獻[12]提出了一種三點垂心法和序列定位相結合的無線傳感網中節點定位的改進算法，即通過得到序列相關系數的前三位最大值，求出與未知節點距離“最近”的三個區域的重心所構成的三角形的垂心，且過濾掉未知節點不可能處在的區域，降低了節點平均定位誤差，該算法增加了估算未知節點精確位置的計算量，但無需增加算法的計算復雜度與傳感器節點的硬件設備，與傳統的三點垂心法與序列定位算法相比，該算法對于節點的定位精度有明顯的提高。文獻[13]提出了一種基于N-最優階次序列的無線傳感網節點定位方法，通過無線信號的衰減模型來產生虛擬測試點，再以參考點為樣本，利用隨機采樣的方法確定最優N值，最后選擇階次為前N位的序列代表的區域，對未知節點的位置進行加權估算，該方法有效減少了節點的定位誤差，并且能在一定程度上提高邊界節點的定位精度。文獻[14]提出了一種基于參考點序列的無線傳感網節點定位算法，該算法將Voronoi圖的頂點作為參考點，從而使信標節點的數目增加，然后利用基于參考點與信標節點到傳感器節點建立的序列等級對傳感器節點的位置進行估算，該算法比質心算法和DV-Hop算法具有更高的定位精度。其中，文獻[12-13]在文獻[11]的基礎上對定位算法進行了改進，但也令其算法的復雜度有所增加，文獻[14]雖首次將Voronoi圖引入到基于信標節點的定位空間區域劃分中，但并未考慮未知節點所處區域信標節點對定位估算的影響。

文獻[15]提出了SLC3V(Sequence Localization Correction algorithm based on 3D Voronoi diagram)，一種基于Voronoi圖原理與階次序列的三維無線傳感器網絡定位算法，該算法利用Voronoi圖對三維定位空間進行區域劃分，構建虛擬信標節點的階次序列表，并通過RSSI方法得到未知節點的定位序列，然后選擇N個最優參數并對其進行等級相關系數的歸一化處理，最后實現對未知節點位置的加權估計，但該算法以假設信標節點的通信半徑能覆蓋整個無線傳感網為研究背景，這就限制了該算法只能應用于定位空間較小的網絡環境，而不適用于覆蓋范圍較大的網絡以及通信環境惡劣的水下傳感網。

本文關注水下三維傳感網的節點定位問題，對上述問題加以考慮，針對信標節點通信半徑非全網的大規模網絡，并結合Voronoi圖劃分原理、序列定位算法和RSD(Regulated Signature Distance)[16]算法，設計一種面向非完全序列的水下三維傳感網定位(Non-Full Sequence-based Localization, NFSL)算法，實現對未知節點位置的加權估算。

2 預備知識

本章簡單介紹3D Voronoi圖[17]在三維定位空間中進行區域劃分的原理以及基于序列的定位算法。

2.1 3D Voronoi圖

Voronoi圖是眾多空間劃分方法之一，它將空間劃分成一定數量的子區域。目前，Voronoi圖已被廣泛應用于各個領域，比如地理信息系統、氣象學以及資訊系統等。許多科研人員利用Voronoi圖來研究無線傳感器網絡中的覆蓋問題。

現給定一個二維平面上傳感器離散點集合P={p1,p2,…,pn}，2≤n<∞，A(x,y)為平面上任意一點，則散點pk(xk,yk)，k∈K={1,2,…,n}與點A的歐氏距離d(pk,A)表示為：

(1)

Voronoi圖基于每個散點將該平面劃分為n個區域，使得每個區域有且僅有一個散點pk，且在散點pk所在Voronoi區域R(pk)中的任意點A滿足下述條件：

R(pk)={A|d(pk,A)≤d(pj,A),?k≠j∧k,j∈K}

(2)

則散點集P的Voronoi圖R(P)由該平面上所有散點的Voronoi區域構成。

由上述可得，2D Voronoi圖是由一組連接每兩個鄰點直線的垂直平分線組成的連續多邊形組成，且該連續多邊形無重疊、無接縫[18-19]，但隨著維數的增長，構成Voronoi圖的單元也由多邊形變成了高維的多面體，因此，構成3D Voronoi圖的單元即為一組三維多面體的集合。如圖1所示，其中，實心圓點表示在三維定位空間內隨機部署的10個信標節點，圖示即為基于10個信標節點的3D Voronoi圖。

最近鄰近性為Voronoi圖的特性之一[20]，即Voronoi子區域內的任意節點到該區域信標節點的歐氏距離小于到其他Voronoi子區域信標節點的歐氏距離，本文正是利用這一特性對三維定位空間進行區域劃分。

2.2 序列定位算法

近年來，許多研究提出基于序列的定位方法，其高效性得益于結合了基于測距與距離無關兩類算法，但目前對序列定位算法的研究大多都以二維空間作為背景[21]。由于序列定位算法在三維空間的應用原理與二維空間相同，且三維空間的圖示較二維空間更為復雜，所以在這里以序列定位算法在二維空間中的應用過程為例作簡單說明：

步驟1 構建二維空間的邊界。

步驟2 利用每兩個相鄰信標節點連線的垂直平分線將邊界內的區域劃分為三類子區域：點、線、面。

步驟3 計算每個子區域的重心(本文將其稱作虛擬信標節點)以及其與各個信標節點之間的距離。

步驟4 確定定位空間中所有虛擬信標節點的定位序列并將其歸入階次序列表中。

步驟5 計算未知節點的定位序列與階次序列表中虛擬信標節點定位序列的等級相關系數，并選擇系數值最大的虛擬信標節點序列作為距離未知節點定位序列“最近”的序列。而該“最近序列”所對應的區域重心即作為未知節點的估測位置。

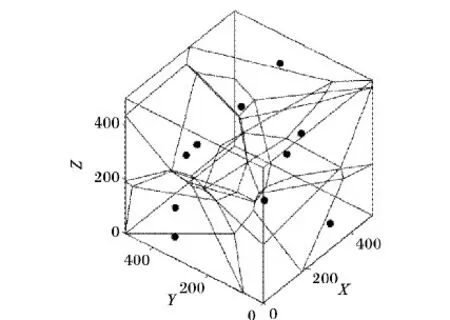
圖1 三維定位空間的Voronoi圖

其中，虛擬信標節點的定位序列與未知節點的定位序列在后面的3.2節中會給出詳細介紹，階次序列表即包含所有虛擬信標節點的定位序列。

圖2為基于4個信標節點的3種區域階次序列確定方法的示例，其中區域1為點，區域2為邊，區域3為面。如上述步驟所示，區域劃分完成后，根據各個子區域的重心到4個信標節點的距離即可得到相應的階次序列(如區域1的階次序列為3113，區域2的階次序列為3211，區域3的階次序列為1243)。

相比其他基于RSSI的定位算法，基于序列的定位算法無需利用RSSI來得到具體的距離參數，它只用來確定未知節點的定位序列，故RSSI方法的固有誤差對本文基于序列的定位算法影響相對較小。

序列定位算法在三維定位空間中的應用是在二維空間中應用的一種拓展與延伸，三維空間被每兩個信標節點連線的垂直平分面劃分出來的3種類型子區域分別為：邊、面、體。

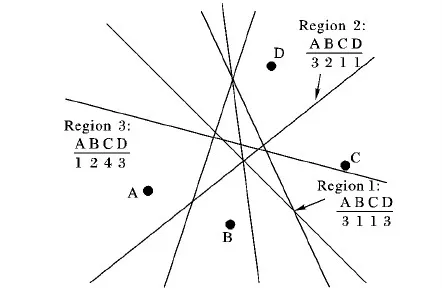
圖2 基于4個信標節點的階次序列示例

3 NFSL算法

水下傳感器網絡的應用場景為三維空間，且Voronoi圖具有高階模型，所以本文考慮將3D Voronoi圖引入到水下傳感網的應用場景中。文獻[22]中提出一種基于序列加權的無線傳感器網絡定位算法，雖然該算法降低了邊緣節點的誤差以及改善了定位精度，但其應用背景為二維定位空間，不適應于水下傳感網的目標定位；文獻[23]提出的一種基于3D Voronoi圖的序列定位算法SL3V (Sequence Localization algorithm based on 3D Voronoi diagram)和文獻[15]提出的一種基于Voronoi圖和階次序列的三維無線傳感器網絡定位算法皆以三維傳感網為背景且信標節點的通信范圍都假設為全網覆蓋，這就導致其無法應用于大規模三維網絡或需昂貴的通信范圍極大的傳感器設備。

針對上述問題，本文提出一種面向非完全序列的水下三維傳感器網絡定位(NFSL)算法。其基本思想為：首先，利用3D Voronoi圖基于三維定位空間中給定的信標節點對該區域進行劃分，并將劃分成的Voronoi多面體中3種區域的幾何中心作為虛擬信標節點；然后，計算每個虛擬信標節點到各個信標節點的距離并得出虛擬信標節點的階次序列以及計算每個信標節點到各個信標節點的距離并得出信標節點的階次序列；接著，通過RSSI方法得到未知節點的非完全階次序列，并利用該序列與所有信標節點的階次序列作相似度比較，選擇與其相似度最大的信標節點作為“最鄰近”信標節點，并將該信標節點的階次序列與其所屬區域所有虛擬信標節點的階次序列列入表中從而構建出與該未知節點相對應的最鄰近序列表；最后，利用修改后的RSD算法計算未知節點序列與其對應的最鄰近序列表中所有序列的相關系數，通過對該系數作歸一化處理并將所得結果作為權重實現對未知節點位置的加權估計。

3.1 三維定位空間的劃分

根據實際的定位環境在三維空間中構造立方體邊界，且信標節點被隨機分布于定位空間中。本文使用3D Voronoi圖劃分三維定位空間，Voronoi多面體產生后，每一個信標節點都在相應的Voronoi多面體內部。為了降低空間劃分的復雜度，本文利用文獻[18]中提出的快速生成3D Voronoi圖方法。

區域劃分完成后，三維定位空間就被每兩個信標節點之間的垂直平分面分隔成了3種類型的區域，即邊、面、體。如圖3所示，其中，實心圓點表示三個信標節點A、B、C。

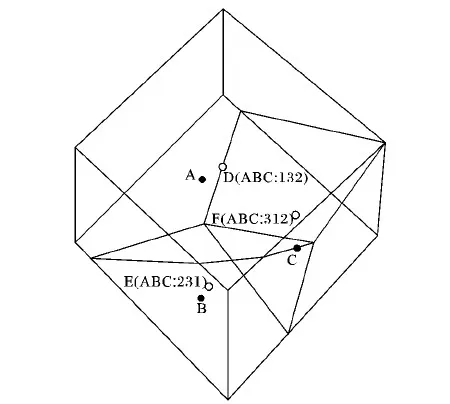
圖3 虛擬信標節點階次序列示例

3.2 階次序列的計算

本文算法涉及到對3種序列的處理，分別為：信標節點的階次序列(與信標節點的定位序列等同，后可類比之)、虛擬信標節點的階次序列和未知節點的階次序列。

3.2.1 信標節點階次序列

作為信標節點，其位置信息皆為已知條件，那么就可以利用兩點距離公式計算一個信標節點與其他信標節點的距離，根據距離的由近到遠將對應的信標節點編號表達成為一個階次序列，則由此方法可得到每個信標節點的階次序列，記為Seq_anch。舉例說明，如表1所示，已編號的5個信標節點A、B、C、D、E，信標節點A距離自己以及其他4個信標節點的距離分別為0，419.469 9，573.551 2，462.814 2，548.015 5，由于與節點A距離從近到遠的信標節點編號分別為：1、2、4、5、3，所以信標節點A的階次序列為12453。

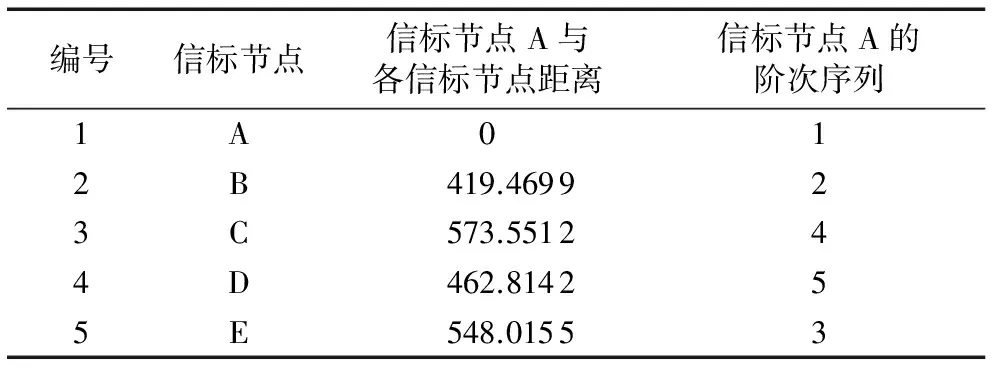
表1 信標節點階次序列的確定

3.2.2 虛擬信標節點階次序列

首先，給出虛擬信標節點的定義：本文將利用3D Voronoi圖劃分出的3種區域(邊、面、體)的幾何中心作為虛擬信標節點。為了簡化運算，每個區域的中心被定義如下：任何邊的中心為其中點，任何面的中心根據文獻[11]中的方法計算，任何體的中心為相應多面體中最遠的兩個點連線的中點。

在給定的三維定位空間中，信標節點的位置信息為已知，則所有虛擬信標節點的位置在區域劃分完成后都已確定并可被推算出來，那么根據虛擬信標節點到各個信標節點距離的遠近就可得到虛擬信標節點的階次序列，記為Seq_vir。虛擬信標節點序列確定的具體過程與3.2.1節中信標節點階次序列的步驟相似。

圖3為虛擬信標節點序列的一個示例，圖中實心圓點A、B、C表示信標節點，空心圓點D、E、F表示虛擬信標節點，且每個虛擬信標節點旁邊都有一個基于距離階次的定位序列。其中，點D為一個邊的中心，由于A點到D點的距離排名為第一位(即A點距離D點最近)，且B點距離D點的距離排名為第三位(即B點距離D點最遠)，所以節點D的階次序列為132。同理，點E是一個體的中心，其階次序列為231，點F為一個面的中心，其階次序列為312。

3.2.3 未知節點階次序列

不同于之前提到過的眾文獻假設所有的未知節點全部位于信標節點的通信范圍內，本文提出的定位算法基于水下大規模三維傳感器網絡且信標節點的通信范圍非全網覆蓋。首先，全網信標節點向周圍的傳感器節點發送數據包，未知節點根據接收到的RSSI值得到其到各信標節點的距離次序從而劃分出該點到各信標節點的位置序列等級，最終確定未知節點的階次序列，記為Seq_unk。

在這里著重說明，由于上文提到的信標節點與虛擬信標節點的階次序列都是基于已知的位置信息而得，所以為全序列，即序列長度為信標節點的總數；而本節提出的未知節點的階次序列是基于RSSI方法而得，由于RSSI會受到通信范圍的影響，且在大規模且通信環境惡劣的水下傳感網中，信標節點通信范圍很難達到全網覆蓋，所以，未知節點的階次序列多為非完全序列(即序列長度小于信標節點的總個數)。

如圖4所示，N1與N2代表兩個未知節點，右邊的序列為其從全網6個信標節點接收到的RSSI值，其中，Inf表示未知節點不在該信標節點的通信范圍內。以圖中的N1為例，其RSSI序列為-147.01，-157.58，-137.25，-154.34，Inf，-156.60，由于RSSI值的大小可以粗略反映未知節點到各信標節點距離的遠近，則該未知節點的階次序列可根據RSSI值的由大到小確定，所以N1的階次序列為3-1-4-6-2(序列不包括與該未知節點無法通信的信標節點的編號)。N2階次序列的確定與N1同理。

圖4 未知節點階次序列示例

3.3 最鄰近序列表的構建

常用的度量2個階次序列相似度的準則為Kendall的Tau指標與Spearman的階次相關系數，但二者的處理對象皆為等長的階次序列，不適用于本文中的非等長序列(信標節點序列與虛擬信標節點序列均為全序列，未知節點序列為非完全序列)，因此，本文借鑒RSD算法對2個非等長階次序列進行相似度度量并得到其階次相關系數，由于該階次相關系數被用作權重，所以本文對該算法稍加修改使其適應于NFSL，修改后的RSD算法可用下式表達：

(3)

其中，K為序列Sm與Sn并集的長度，SD(Sm,Sn)為顯性、隱性、可能性3種翻轉對數量之和[16]，則據式(3)得到的結果RSD′(Sm,Sn)即為序列Sm與Sn的階次相關系數(即二者的相似度)，其范圍為[0,1]，在3.4節中將其作為權重對未知節點的位置作加權估計。

針對給定未知節點X(x,y,z)的階次序列S，利用式(3)計算序列S與所有信標節點序列的階次相關系數，選擇系數最大的信標節點作為未知節點X的“最鄰近”信標節點Nb，并將其置于最鄰近序列表T中，另外，將Nb所處Voronoi子區域中所有虛擬信標節點的階次序列也置于T中。由此，未知節點X的最鄰近序列表T={T1,T2,…,Tn}即可被確定，其中T1為信標節點Nb的階次序列，T2到Tn為Nb所屬子區域中所有虛擬信標節點的階次序列。

3.4 未知節點位置的加權估計

給定未知節點X(x,y,z)的定位序列W，本文算法根據3.3節中介紹的方法構建X的最鄰近序列表T={T1,T2,…,TN},計算出W與T中每個序列的階次相關系數(該系數已歸一化)并將其作為權重，最后結合最鄰近序列表T中各個序列相對應的節點坐標進行未知節點位置的加權估計，則未知節點X(x,y,z)的坐標可表示為：

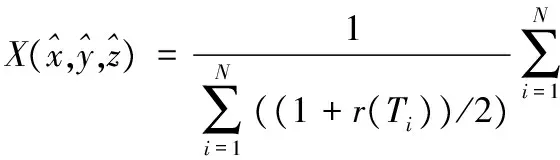
(4)

其中：r(Ti)表示未知節點序列W與最鄰近序列表T中序列Ti的階次相關系數，Ci表示T中第i個序列Ti對應的坐標。

3.5 NFSL算法偽代碼展示

本節綜合3.1～3.4節內容，給出NFSL的算法流程。首先，根據已知的信標節點坐標矩陣N，計算信標節點階次序列Seq_anchi以及空間劃分后所得虛擬信標節點的坐標矩陣V，根據N與V計算出所有虛擬信標節點階次序列Seq_virj；其次，根據給定未知節點X的RSSI矩陣S，計算未知節點階次序列Seq_unkk；然后，利用式(3)計算未知節點序列與所有信標節點序列的階次相關系數，并取值最大的信標節點作為該未知節點的“最鄰近”信標節點Nb，Nb的階次序列記為S_anch，將Nb與其所處Voronoi子區域中所有虛擬信標節點的階次序列置于最鄰近序列表T中，其對應坐標置于坐標集C中；最后，利用式(3)計算出未知節點序列與T中每條序列的階次相關系數r(Ti)，并將其作為權重，利用式(4)實現未知節點X位置的加權估計。

偽代碼如下所示。

算法1 NFSL算法。

Input: Coordinates matrix of anchorsN, RSSI matrixS

for each anchornido

Compute theSeq_anchiof all anchors

end for

Compute coordinates matrix of vir_anchorsV

for each vir_anchorvjdo

ComputeSeq_virjof all vir_anchors

end for

Compute theSeq_unkkof all unknown nodes

for unknown nodeXdo

ComputeRSD′(Seq_unkk,Seq_anchi)

according to Eqn. (3)

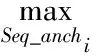
ConstructCandT

Computer(Ti) =RSD′(Seq_unkk,Ti)

according to Eqn. (3)

Compute coordinate ofXaccording to Eqn. (4)

end for

Output: Coordinates matrix of unknown nodes

4 仿真結果與性能分析

本文利用Matlab仿真軟件對提出的定位算法進行仿真，評估其性能，并與DV-Hop、質心算法等經典定位算法進行比較。本章采用的仿真環境為：500個節點隨機分布于500 m×500 m×500 m的正方體區域內，其中，信標節點比例為0.3，節點通信半徑均為200 m。以上參數均為默認值，下文仿真中除個別對比參數(如信標節點比例、通信半徑、節點總數和網絡規模)作為變量以外，其余變量均為默認值。另外，本文仿真結果中的定位誤差是指節點的實際定位誤差(m)與節點通信半徑(m)的比值。如圖5所示，圖中所有參數皆為默認值。

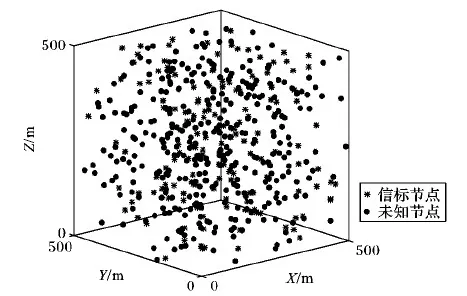
圖5 仿真節點分布

4.1 通信開銷分析

在DV-Hop中，信標節點向鄰居節點廣播自身位置，接收節點記錄到每個信標節點的最小跳數并轉發給下一跳鄰居節點，最終每一個未知節點可以得到與每一個信標節點的最小跳數；但在NFSL與質心算法中，每個未知節點僅接收通信范圍內所有信標節點的通信信息而不再向鄰居節點轉發，由此就可獲得NFSL中未知節點距離信標節點的階次序列和質心算法中所有與該未知節點連通的信標節點位置信息。綜上可得，本文算法與質心算法的通信開銷大致相同，且小于DV-Hop的通信開銷。

4.2 信標節點數的影響

信標節點占總節點的比例稱為信標節點比例，信標節點比例的大小將直接影響本文算法的定位精度。圖6(a)～(c)分別表示信標節點比例對本文提出算法、DV-Hop、質心(Centroid)算法3種算法的平均定位誤差、最大定位誤差與最小定位誤差的影響。從圖中可以發現在信標節點以0.15，0.2，0.25，0.3，0.35，0.4的比例逐漸遞增的情況下，本文算法的平均定位誤差由約0.32下降至約0.23，DV-Hop由約0.33微降至約0.3，質心算法則由約0.34降至約0.29，雖然3種算法的定位誤差都在逐漸遞減，但本文算法的定位效果提高最快。表明在信標節點比例增多時，本文算法的定位精度具有更為明顯的優勢。

4.3 節點通信半徑、節點總數與網絡規模的影響

本文算法的定位精度受多種因素影響，因此本節進一步在不同通信半徑、節點總數與網絡規模的情況下對算法進行了評估。圖7(a)為通信半徑對本文算法與經典定位算法的平均定位誤差影響對比圖，從圖中可以看出，通信半徑對3種算法的影響不盡相同，其中，隨著通信半徑以25 m為間隔從150 m擴大至300 m的情況下，本文算法的平均定位誤差從約0.35下降至約0.17，然DV-Hop的定位精度無明顯波動，質心算法的定位精度與之降低，定位誤差增至約0.38左右。

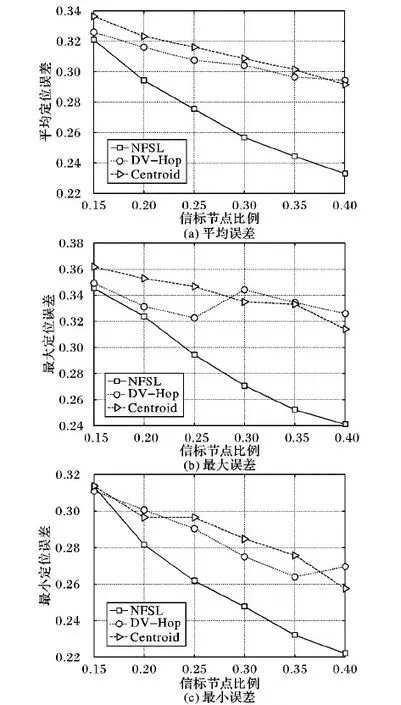
圖6 信標節點比例對定位誤差的影響

圖7(b)為本文算法、DV-Hop算法和質心算法平均定位誤差在節點總數增加影響下的變化趨勢。可以看出，在信標節點比例不變而節點總數以50為間隔從300增至600的情況下，本文算法的定位誤差從約0.31降至約0.24，而質心算法的定位誤差則由約0.33降至約0.3，對比之下，本文算法定位精度的提高速度遠超于質心算法，這是由于信標節點數隨節點總數的增加而增加的原因，說明未知節點的數量對本文算法的影響微乎其微。圖中DV-Hop算法的定位誤差曲線無太大波動，說明在信標節點比例一定時，DV-Hop算法的定位精度受節點總數變化的影響不明顯，這與該算法的性質有關。

圖7(c)表示在網絡規模以50 m為間隔從300 m(長、寬、高均為300 m)擴大至450 m的情況下本文算法與另兩種傳統定位算法的定位誤差對比圖。由圖可得，網絡規模對本文算法的定位精度有一定影響，網絡規模越小定位精度就越高。即使在網絡規模較大(網絡規模為450 m×450 m×450 m)的情況下，相較于另兩種算法的誤差值(DV-Hop:約0.3，Centroid:約0.33)，本文算法仍具有較低的定位誤差值，約為0.23。

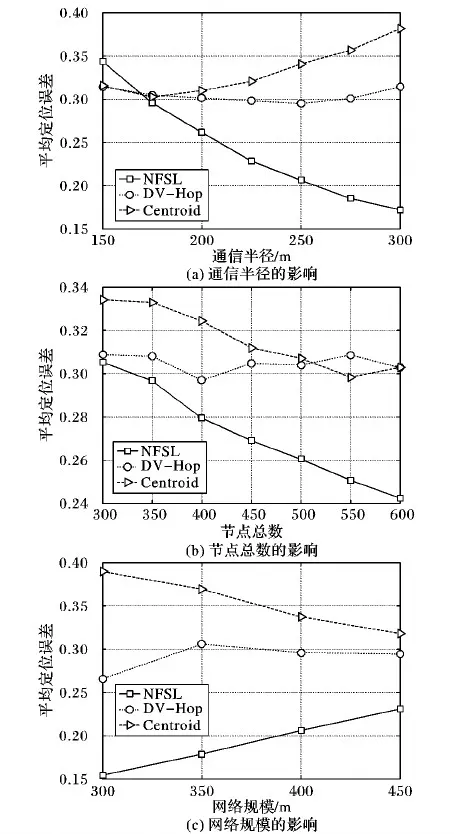
圖7 3種變量對平均定位誤差的影響

仿真結果表明，本文算法在通信開銷小于或大致相同于另兩種定位算法的情況下，在多種影響因素下均具有較高的定位精度，與傳統定位算法相比其定位精度最大可提高約23%。

5 結語

本文提出一種面向非完全序列的水下三維傳感網定位算法。利用3D Voronoi圖對定位空間進行區域劃分，將劃分后得到的Voronoi子區域邊的中心、面的中心與體的中心作為虛擬信標節點并得到其階次序列，比較由RSSI得到的未知節點序列與信標節點序列的階次相關系數并構建最鄰近序列表，最終，利用改進后的RSD算法計算未知節點序列(非完全序列)與對應的最鄰近序列表中各序列(全序列)的階次相關系數，將該系數作為權重并結合對應節點坐標實現對未知節點位置的加權估計。仿真結果表明，在不增加任何硬件的情況下，本文算法有效提高了定位精度，與傳統定位算法相比定位精度最大可提高約23%。

References)

[1] DU X D, JI J T, YAN D P. Application research of wireless sensor network in intelligent transportation system [J]. Advanced Materials Research, 2010, 108/109/110/111: 1170-1175.

[2] LIU L, WU X, ZHU Z, et al. A localization algorithm based on beacon error problem in underwater wireless sensor network [C]// Proceedings of the 15th IEEE International Conference on Communication Technology. Piscataway, NJ: IEEE, 2013: 478-482.

[3] WALDMEVER M, TAN H P, SEAH W K G. Multi-stage AUV-aided localization for underwater wireless sensor networks [C]// Proceedings of the 25th IEEE International Conference on Advanced Information Networking and Applications Workshops. Washington, DC: IEEE Computer Society, 2011: 908-913.

[4] BAHL P, PADMANABHAN V N. RADAR: an in-building RF-based user location and tracking system [C]// Proceedings of the 19th Annual Joint Conference of the IEEE Computer and Communications Societies. Piscataway, NJ: IEEE, 2000: 775-784.

[5] 肖竹,譚光華,李仁發,等.無線傳感器網絡中基于超寬帶的TOA/AOA聯合定位研究[J].計算機研究與發展,2013,50(3):453-460.(XIAO Z, TAN G H, LI R F, et al. Joint TOA/AOA localization based on UWB for wireless sensor networks [J]. Journal of Computer Research and Development, 2013, 50(3): 453-460.)

[6] 吳紹華，張欽宇，張乃通.UWB無線傳感器網絡中基于匹配濾波檢測的TOA估計[J].軟件學報,2009,20(11):3010-3022.(WU S H, ZHANG Q Y, ZHANG N T. TOA estimation based on match-filtering detection for UWB wireless sensor networks [J]. Journal of Software, 2009, 20(11): 3010-3022.)

[7] 陳鴻龍，李鴻斌，王智.基于TDoA測距的傳感器網絡安全定位研究[J].通信學報,2008,29(8):11-21.(CHEN H L, LI H B, WANG Z. Research on TDOA-based secure localization for wireless sensor networks [J]. Journal on Communications, 2008, 29(8): 11-21.)

[8] ADEMUWAGUN A, FABIO V. Reach centroid localization algorithm [J]. Wireless Sensor Network, 2017, 9: 87-101.

[9] HOSSEINIRAD S M, POURDEILAMI J, NIAZI M, et al. On improving APIT algorithm for better localization in WSN [J]. Journal of AI & Data Mining, 2013, 2(2): 97-104.

[10] ZHANG A, YE X, HU H, et al. Improved DV-HOP positioning algorithm based on one-hop subdivision and average hopping distance modification [J]. Chinese Journal of Scientific Instrument, 2012, 33(11): 2552-2559.

[11] YEDAVALLI K, KRISHNAMACHARI B. Sequence-based localization in wireless sensor networks [J]. IEEE Transactions on Mobile Computing, 2007, 7(1): 81-94.

[12] 劉志華,陳嘉興,陳霄凱.無線傳感器網絡中序列定位新算法的研究[J].電子學報,2010,38(7):1552-1556.(LIU Z H, CHEN J X, CHEN X K. A new algorithm research of sequence-based localization technology in wireless sensor networks [J]. Acta Electronica Sinica, 2010, 38(7): 1552-1556.)

[13] 裴忠民,鄧志東,徐碩,等.一種基于N-最優階次序列的無線傳感器網絡節點定位方法[J].自動化學報,2010,36(2):199-207.(PEI Z M, DENG Z D, XU S, et al. A new localization method for wireless sensor network nodes based onN-best rank sequence [J]. Acta Automatica Sinica, 2010, 36(2): 199-207.)

[14] 劉影,錢志鴻,孫大洋.基于參考點序列的無線傳感器網絡節點定位算法[J].吉林大學學報(工學版),2012,42(2):489-493.(LIU Y, QIAN Z H, SUN D Y. Node localization scheme for wireless sensor networks based on reference node sequence [J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(2): 489-493.)

[15] LIU J, YAN F, YANG X. 3D localization algorithm based on Voronoi diagram and rank sequence in wireless sensor network [J]. Scientific Programming, 2017, 2017(4): Article No. 4.

[16] ZHONG Z, HE T. RSD: a metric for achieving range-free localization beyond connectivity [J]. IEEE Transactions on Parallel & Distributed Systems, 2011, 22(11): 1943-1951.

[17] ALMASHOR M, KHALIL I. Reducing network load in large-scale, peer-to-peer virtual environments with 3D Voronoi diagrams [C]// Proceedings of the 17th International Conference on High Performance Computing. Washington, DC: IEEE Computer Society, 2010: 1-10.

[18] HWANG G J, ARUL J M, LIN E, et al. Design and multithreading implementation of the wave-front algorithm for constructing Voronoi diagrams [C]// ICA3PP: Proceedings of the 6th International Conference on Algorithms and Architectures for Parallel Processing. Berlin: Springer, 2005: 257-266.

[19] LIU J Y, LIU S. A survey on applications of Voronoi diagrams [J]. Journal of Engineering Graphics, 2004, 25(2): 125-132.

[20] DU Q, GUNZBURGER M, JU L L. Advances in studies and applications of centroidal Voronoi tessellations [J]. Numerical Mathematics: Theory, Methods and Applications, 2010, 3(2): 119-142.

[21] 陳嘉興,劉志華.無線傳感器網絡節點的三維序列內心定位算法[J].南京理工大學學報(自然科學版),2011, 35(3): 371-375.(CHEN J X, LIU Z H. 3D Sequences and incenters localization algorithm for nodes in WSN [J]. Journal of Nanjing University of Science & Technology, 2011, 35(3): 371-375.)

[22] 胡敏.基于階次序列加權的無線傳感器定位算法[J].計算機工程與應用,2014,50(10):116-119.(HU M. Node localization algorithm of wireless sensor networks based on optimal weighted rank sequences [J]. Computer Engineering and Applications, 2014, 50(10): 116-119.)

[23] YANG X, LIU J. Sequence localization algorithm based on 3D Voronoi diagram in wireless sensor network [J]. Applied Mechanics & Materials, 2014, 644-650: 4422-4426.

This work is partially supported by the National Key Research and Development Program of China (2016YFC060908), the National Natural Science Foundation of China (51674255), the Production-Study-Research Joint Prospective Research Project of Jiangsu Province (BY2014028- 09).

CHEDi, born in 1994, M. S. candidate. Her research interests include sensor network, ocean observing network.

NIUQiang, born in 1974, Ph. D., professor. His research interests include machine learning, data mining.