基于反步法非線性純反饋系統的控制器設計

賈付金，蔣 沅

(南昌航空大學 信息工程學院，南昌 330000)(*通信作者電子郵箱3394044951@qq.com)

0 引言

與一般非線性系統如下三角系統或者嚴格反饋非線性系統相比較，非線性純反饋系統[1-2]是更一般的系統，更能反映實際事物的情況，因此近幾年來受到廣泛的關注，成為研究的熱門。

1991年Kanellakopoulos等[3]較早地提出并研究了一類純反饋非線性控制問題，按照反步法的思想，經過坐標變換，給出了嚴格反饋系統全局調節和全局跟蹤的自適應控制器設計方法。然而，由于純反饋非線性系統存在非仿射函數，這給控制器的設計帶來了困難，也因此傳統適合于嚴格反饋的非線性系統的控制器設計方法很難直接用于解決純反饋非線性系統的控制問題。在文獻[3]的基礎上，Seto等[4]針對一類純反饋系統控制，在沒有使用任何狀態變換的情況下，基于自適應理論[5-7]，設計出了使得系統全局調節和全局跟蹤的控制器設計方法，但是該方法不能保證系統全局有界，然而，系統全局有界又是控制理論最基本的要求。為此，劉勇華[8]研究了純反饋系統的跟蹤問題，提出了一種新的坐標變換，利用反步法，遞推出了可使跟蹤誤差漸近的穩定和全局信號有界的控制器；但是根據文獻[9-10]可知，純反饋系統會存在狀態的非仿射性函數和控制輸入的非仿射性函數，劉勇華[8]只解決了狀態存在的非仿射結構，而沒有解決控制輸入的非仿射性問題。于是，曾喆昭等[11]針對一類單輸入單輸出非仿射性非線性系統，結合滑模控制方法[12-13]，提出了一種自學習滑膜抗擾控制，最終可使得系統跟蹤誤差漸近穩定和全局有界；只是曾喆昭等[11]研究的對象只是針對二階系統，對于大于二階的系統該方法則無能為力。對此，胡云安等[14]以n階非仿射性純反饋系統作為研究對象，結合神經網絡理論和反步法，提出了自抗擾控制器；但由于引入較多的變量和復雜的公式計算，這樣使得該方法較為復雜。所以，如何相對簡單地設計出能夠使得非線性純反饋系統的跟蹤誤差漸近穩定和全局漸近有界的控制器是一個值得注重的問題。

對于狀態存在的非仿射性結構項而言，避免傳統坐標變換的弊端，本文從另一角度提出了一種非傳統狀態變換，經過變換后，設計虛擬控制器，可使新狀態之間呈現出線性關系，所以設計控制器相對于以往的狀態變換來說更容易。對于非仿射控制輸入可能存在的非仿射性項，在利用上述非傳統坐標變換遞推時，會有多個控制器存在的問題，對于這種情況，本文引入了一個關于控制輸入的輔助控制系統。這樣，不僅能成功地解決對于這類非仿射性控制輸入的難得到問題和多樣性問題，而且與反步法結合構造出的輔助控制器，可使得純反饋系統狀態全局有界和能夠跟蹤到給定信號，也即跟蹤誤差趨于為零。最后，仿真實驗將本文與文獻[8,11]中仿真實驗系統的仿真效果作了比較，說明了本文提出的算法的優越性。

1 系統和問題描述

考慮如下非線性純反饋系統：

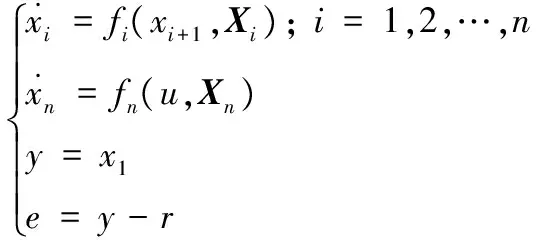
(1)

其中：(x1,x2,…,xn)∈Rn為系統已知狀態，Xi=(x1,x2,…,xi)∈R1×i；u∈R為控制輸入；fi(xi+1,Xi)是帶有系統狀態xi+1的光滑非仿射性已知函數；fn(u,Xn)是帶有控制輸入u的光滑非仿射性已知函數；y∈R為系統輸出；r為有界且n+1階導數也有界的跟蹤信號。

在進行控制器設計時,為避免出現系統的能控問題,作出如下假設。

假設1 對于函數fi,fn，使得在任意時刻

(2)

這樣,就避免了系統(1)出現能控性問題。

對于系統(1),由于非仿射非線性函數fn的存在,使得控制器u的設計很困難。為此，引入式(3)控制器輔助的一階系統：

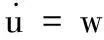
(3)

其中:w為待定函數。從某種意義上說，引入式(3),是把控制輸入看成系統狀態，只要設計出待定函數w，任意初始值的控制輸入也就生成，從而避免了過多繁雜的公式計算。

問題描述 對于以上純反饋系統(1)和輔助系統(3)組成的增廣系統,通過非傳統坐標變換,利用反步法(Backstepping)和Lyapunov函數設計出輔助控制器w,使得系統全局漸近穩定有界,且跟蹤誤差趨于穩定。為清晰說明本文的設計思路,在此給出其控制方案流程如圖1所示。

2 控制器設計

為了設計控制器，使得非線性系統(1)全局穩定有界，避免非仿射性性函數帶來的復雜性，現在定義如下形式的非傳統狀態變換式(4)：

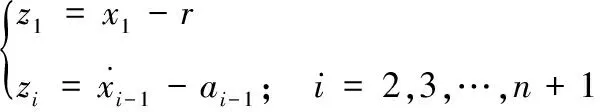
(4)

其中：(a1,a2,…,an)為虛擬控制器，且xn+1=u。

在傳統變換[15]中,常常把xi+1為第i個子系統的虛擬控制器，也因此采取的變換為：

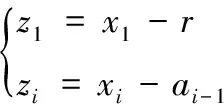
(5)

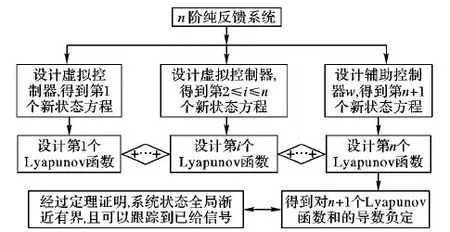
圖1 控制方案流程

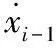
基于反步法和非傳統狀態變換(4)，控制器設計的具體步驟如下。

1)第1步。

根據式(1)和式(4)可知：

(6)

設虛擬控制器：

(7)

其中c1為待定正常數。

把式(7)代入式(6)得：

(8)

設Lyapunov函數為：

根據式(8)，能夠得：

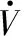
(9)

2)第2步。

根據式(1)和式(4)可知：

(10)

設虛擬控制器為：

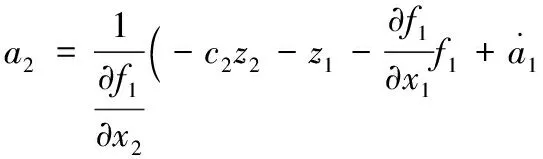
(11)

其中c2為待定正常數。

把式(11)代入式(10)得：

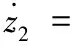
(12)

設Lyapunov函數為：

根據式(12)，能夠得：

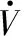
(13)

3)第3≤i≤n-1步。

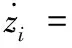
(14)

設虛擬控制器為：

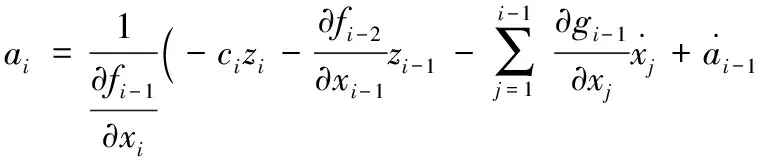
(15)

其中ci為待定正常數。

把式(15)代入式(14)得：

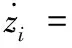
(16)

設Lyapunov函數為：

根據式(16)，能夠得：

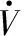
(17)

4)第n步。

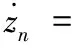
(18)

設虛擬控制器為：

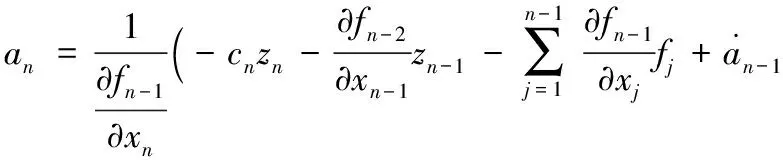
(19)

其中cn為待定正常數。

把式(19)代入式(18)得：

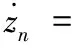
(20)

設Lyapunov函數為：

根據式(20)，能夠得：

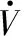
(21)

5)第n+1步。

(22)

設輔助控制器為：

(23)

其中cn+1為待定正常數。

把式(23)代入式(22)得：

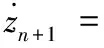
則可以得到：

(24)

定理1 對于滿足假設1的非線性純反饋系統(1),采用輔助控制器(23),則系統跟蹤誤差全局漸近有界，切閉環系統所有信號全局有界。

證明 選取如下Lyapunov函數：

結合上述推導過程，對V求導得：

(25)

其中，λ=min{2c1,2c2,…,2cn+1}。

對式(25)兩邊沿著[0,t]積分，可得：

V=V(0)e-λt

(26)

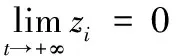
證畢。

3 數值仿真

例1 考慮文獻[11]中的非線性仿真系統，如式(27)所示：

(27)

其中:(x1,x2)為系統狀態；u∈R為控制輸入；y∈R為系統輸出；x2+x23/5為狀態非仿射性結構；u+u3/7控制輸入非仿射性結構；e為跟蹤誤差，跟蹤信號用文獻[11]中的r=sin(t) cos(t)。

由于：

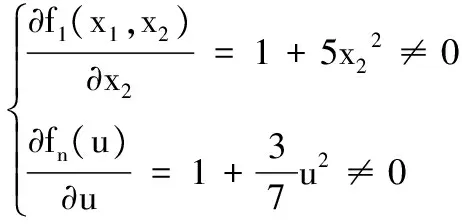
(28)

可知滿足假設1，則同樣可以用本文提出的方法解決系統(27)的跟蹤問題。

根據上述理論和式(23)，通過理論推導得出輔助控制器：

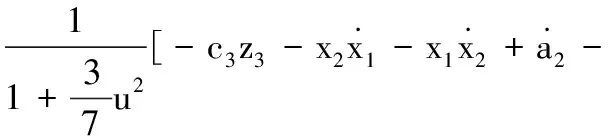
(1+3x22+5x24)z2]

(29)

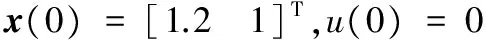
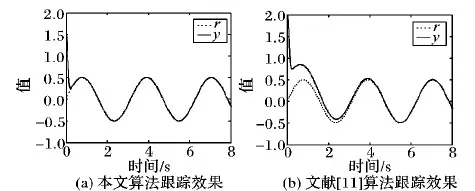
圖2 兩種算法跟蹤效果對比(例1)

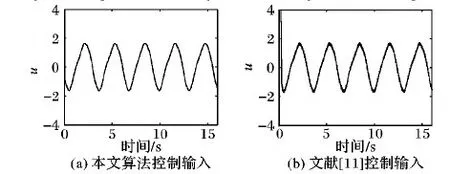
圖3 兩種算法控制律u對比(例1)

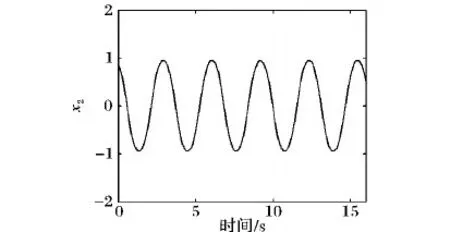
圖4 本文算法仿真的系統狀態x2(例1)

Fig. 4 Simulation system statusx2of the proposed algorithm for example 1

從圖2(a)、圖3可以綜合看出，本文所提供的算法可保證系統(27)跟蹤誤差全局漸近穩定，且閉環系統有界。

在相同的系統(27)下，在圖2中：由圖2(a)可知輸出y大約用0.5 s跟蹤到跟蹤信號r，且沒有階躍；而利用文獻[11]提供的算法仿真得到圖(b)，控制輸出y大約用4.5 s跟蹤到跟蹤信號r，且大約在0.2 s處有一定的階躍。所以相比之下，本文的算法在跟蹤效果上較快，且沒有階躍。

同樣，在控制u仿真的效果對比上，如圖3(a)和(b)所示，不難看出，本文的仿真效果圖3(a)與利用文獻[11]算法仿真效果圖3(b)相比，本文算法仿真出的圖像沒有階躍，且沒有高頻的抖振現象。

例2 考慮文獻[8]的仿真實例中的非仿射性非線性系統，如式(30)：

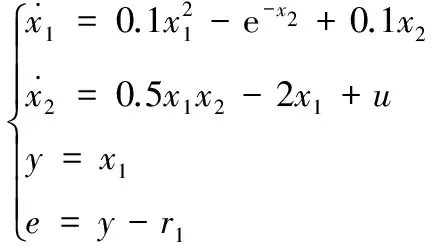
(30)

其中:(x1,x2)為系統狀態；u∈R為控制輸入，由于系統(30)不存在輸入控制的非仿射結構，但是函數-e-x2+0.1x2為狀態非仿射性結構,所以可用本文提出的非傳統狀態變換來處理；y∈R為系統輸出；e為跟蹤誤差；為了更好地與文獻[8]作比較，現取文獻[8]仿真實例中的跟蹤信號r=1.5 sin(2t)。

由于：

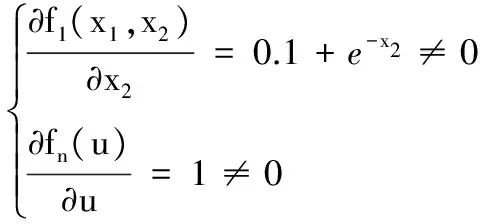
(31)

可知滿足假設1，則可以用本文提出的方法解決系統(30)的跟蹤問題。

根據上述理論和非傳統狀態變換(4)，通過理論推導控制器：

(32)

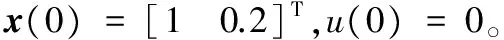
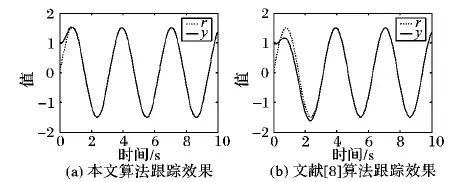
圖5 兩種算法跟蹤性能對比(例2)

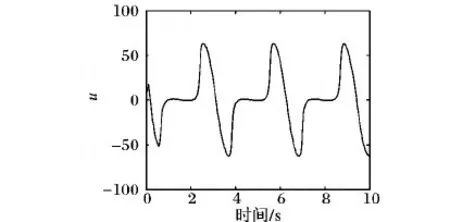
圖6 本文算法仿真的控制律u(例2)

從圖5(a)、圖6以及圖7可以綜合地看出，本文所提供的算法可保證系統跟蹤誤差漸近穩定，且閉環系統信號有界。

在相同的系統(30)下，由圖5(a)可知輸出y大約用1 s跟蹤到跟蹤信號r；而利用文獻[8]提供的算法仿真得到圖5(b)，控制輸出y大約用3 s跟蹤到跟蹤信號r。所以可以得知本文的算法跟蹤效果較快。

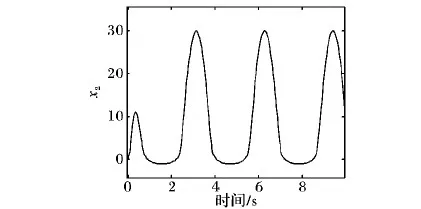
圖7 本文算法仿真的狀態x2(例2)

Fig. 7 Simulation system statusx2of the proposed algorithm for example 2

4 結語

本文研究了一類純反饋非線性系統輸出跟蹤問題，利用了不同于傳統的反推法，提出了一個新的狀態變換，并且引用輔助系統(3)，在滿足假設1的前提下，利用Backstepping反推法，設計出輔助控制器(23)，使得純反饋系統具有下面結論：

2)與文獻[4]相比較，本文所得到得控制器可使得系統輸出誤差漸近穩定，且可以保證閉環系統所有信號有界，而文獻[4]方法討論了系統輸出誤差問題，沒有考慮系統全局問題。

3)與文獻[16]相比較，對于控制輸入存在的非仿射結構而言，本文僅僅引入了一階輔助系統可以解決文獻[16]中研究的問題，而文獻[16]需要結合魯棒控制理論和復雜的公式運算來完成控制器的設計，相比之下，本文在公式計算上簡易。

References)

[1] LABIOD S, GUERRA T M. Adaptive fuzzy control of a class of SISO nonaffine nonlinear systems [J]. Fuzzy Sets and Systems, 2007, 158(10): 1126-1137.

[2] WANG D, HUANG J. Adaptive neural network control for a class of uncertain nonlinear systems in pure-feedback form [J]. Automatica, 2002, 38(8): 1365-1372.

[3] KANELLAKOPOULOS I, KOKOTOVIC P V, MORSE A S. Systematic design of adaptive controllers for feedback linearizable systems [J]. IEEE Transactions on Automatic Control, 1991, 36(11), 1241-1253.

[4] SETO D, WNNASWAMY A M, BAILLIEUL J. Adaptive control of nonlinear systems with a triangular structure [J]. IEEE Transactions on Automatic Control, 1994,39(7):1411-1428.

[5] TONG S C, LI Y M. Observer-based adaptive fuzzy backstepping control of uncertain nonlinear pure-feedback systems [J]. Science China Information Sciences, 2014, 57(1): 012204:2-012204:14.

[6] HUANG H, ZHANG Z. Characteristic model-based H2/H∞ robust adaptive control during the re-entry of hypersonic cruise vehicles [J]. Science China Information Sciences, 2015, 58(1): 012202:1-012202:21.

[7] MA K M, MENG G Z, ZHANG J W. Output regulation for a class of uncertain systems via fuzzy adaptive control [C]// Proceedings of the 2012 31st Chinese Control Conference. Piscataway: IEEE, 2012: 969-974.

[8] 劉勇華.一類純反饋非線性系統的反推控制[J].控制理論與應用,2014,31(6):801-804.(LIU Y H. Backstepping control for a class of pure-feedback nonlinear systems [J]. Control Theory & Applications, 2014, 31(6): 801-804.)

[9] LI Y, ZHANG J H, WU X. Adaptive control of uncertain non-affine pure feedback nonlinear systems using backstepping techniques [C]// Proceeding of the 2014 33rd Chinese Control Conference. Piscataway: IEEE, 1829-1833.

[10] TONG S C, LI Y M. Adaptive fuzzy output feedback backstepping control of pure-feedback nonlinear systems via dynamic surface control technique [J]. International Journal of Adaptive Control and Signal Processing, 2013, 27(7): 541-561.

[11] 曾喆昭,吳亮東,楊振源,等.非仿射系統的自學習滑模抗擾控制[J].控制理論與應用,2016,33(7):980-987.(ZENG Z Z, WU L D, YANG Z Y, et al. Self-learning sliding-mode disturbance rejection control for non-affine systems [J]. Control Theory & Applications, 2016, 33(7): 980-987.)

[12] REN L T, XIE S S, MIAO Z G, et al. Fuzzy robust sliding mode control of a class of uncertain systems [J]. Journal of Central South University, 2016, 23(9): 2296-2304.

[13] SHANG W, TANG S J, GUO J. Robust sliding mode control with ESO for dual-control missile [J]. Journal of Systems Engineering and Electronics, 2016, 27(5): 1073-1082.

[14] 胡云安,程春華,鄒強,等.非仿射純反饋系統的間接自適應神經網絡控制[J].控制理論與應用,2014,31(4):467-478.(HU Y A, CHENG C H, ZOU Q, et al. Indirect adaptive neural networks controller for non-affine pure-feedback systems [J]. Control Theory & Applications, 2014, 31(4): 467-478.)

[15] KRSTIC M, KANELLAKOPOULOS I, KOKOTOVIC P V. Nonlinear and Adaptive Control Design [M]. New York: John Wiley & Sons, 1995: 136-159.

[16] 張強,吳慶憲,姜長生,等.基于Backstepping的非仿射性非線性系統魯棒控制[J].控制與決策,2014,29(1):19-26.(ZHANG Q, WU Q X, JIANG C S, et al. Robust control for nonaffine nonlinear systems based on backstepping [J]. Control and Decision, 2014, 29(1): 19-26.)

This work is partially supported by the National Natural Science Foundation of China (61663030, 61663032), the Natural Science Foundation of Jiangxi Province (20142BAB207021), the Scientific and Technological Project of Jiangxi Educational Committee (GJJ150753), the Open Foundation of Key Laboratory of Nondestructive Testing (Nanchang Hangkong University), Ministry of Education (ZD29529005), the Innovaion Fund Designated for Graduate Students of Nanchang Hangkong University (YC2016-S350), the “Small Invention, Small Manufacture, Small Creation” Key Projects of the Twelfth of Nanchang Hangkong University (2017ZD021).

JIAFujin, born in 1988, M. S. candidate. His research interests include nonlinear system theory, output regulation theory.

JIANGYuan, born in 1982, Ph. D., associate professor. His research interests include aircraft control design, motor control and optimization.