數學課堂巧用錯誤資源摭談

張秀花

【摘要】數學課堂巧用錯誤資源，挖掘錯誤背后的有效教學因素，豐富教學內容。以誤導正，讓錯誤成為學生認知的“轉折點”，思維飛躍的“起跳板”，互學共進的“融合劑”，打造“學”的課堂，讓兒童的數學學習真實發生。

【關鍵詞】課堂教學；數學思維；錯誤；生成

英國心理學家貝恩布里奇說過： “錯誤人皆有之，作為教師不利用是不可原諒的。”數學課堂教學中，學生的錯誤真實地反映了學生的疑惑和誤解，作為教師，我們需要把錯誤看作有效的課堂教學資源，善于引導學生識“錯”、 析“錯”、思“錯”、悟“錯”，激發探究的興趣，點燃思維的火花，對概念進行正確理解并深化，從而將錯誤糾正過來，將它變成寶貴的學習資源，讓“錯誤”成為“正確”的先導。

一、巧用錯例，以錯導學

哲學家黑格爾先生說得好：“錯誤本身乃是達到真理的一個必然的環節。”真實的數學課堂，學生出錯是司空見慣的情況，教師要適時、巧妙地分析引導，引發認知沖突，這能有效激發學生探究新知的興趣。如一位老師教學“平均數”，新課伊始，創設套圈游戲，教者依次呈現男生和女生各1名、男生和女生各2名、男生和女生各3名、男生和女生各4名的套圈成績，學生均能用比多、比少、比總數，得出男女生的套圈成績。最后，教者呈現4名男生和5名女生的套圈成績統計圖（如右圖），提出問題：男生套得準一些還是女生套得準一些，怎么比較呢？問題在學生中引起了不同意見的爭論，有的認為比較男生和女生中套得最多的個數，有的認為比較男生和女生套中的總個數。教者順勢而導，啟發學生思考，你認為哪種比較方法是合理的？學生再次產生爭論，發現兩種比較方法都不合理，產生探究新知的心理需求，思考合理有效的比較方法，進而引入“平均數”這一新概念的學習。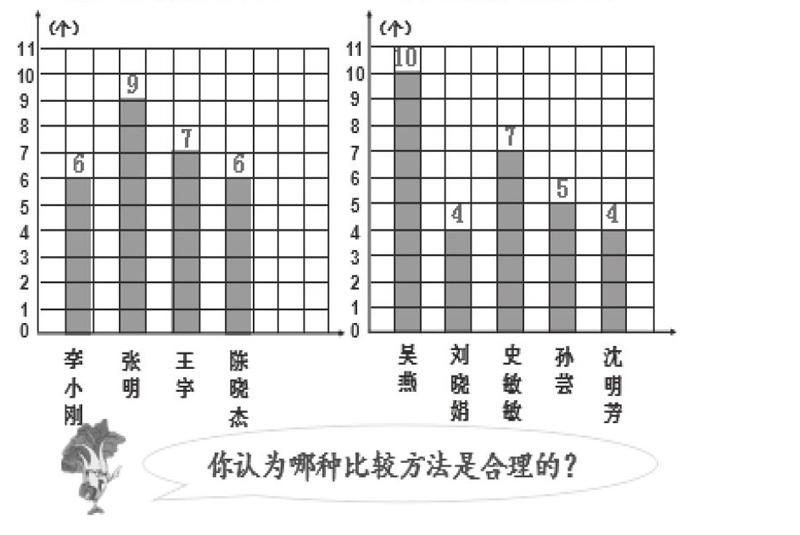

下面仍以“平均數”為例，學生要有效建構“平均數”的新概念，離不開練習的鞏固與應用，教師就應為學生提供一些有益于突破知識難點的典型錯例，讓學生識別錯誤，針對錯誤要點，引導學生進一步加深對知識的理解與掌握。這里，教者在學生初步理解平均數的含義及掌握求平均數的方法后，引入一組生活中的實例讓學生比較辨析：①王力是學校足球隊員，他身高145厘米，可能嗎？學校足球隊可能有身高超過150厘米的隊員嗎？②小軍想下水學游泳，池塘的平均水深100厘米。小軍問：“我身高145厘米，下水游泳有危險嗎？”你們覺得他下水游泳有沒有危險呢？③小兵走6步，共走了330厘米，他每一步都走了55厘米，對嗎？④電梯里有5人，他們體重的和是310千克，每個人的體重都是62千克，對嗎？通過典型的錯例，教師可以引導學生展開討論，運用所學的平均數的知識判斷和分析對錯，體會平均數只是代表一組數據的整體水平，實際數值可能遠遠高于平均數，也可能低于平均數，加深學生對平均數實際意義的理解。

二、巧用錯解，以錯助學

布魯納說過：“學生的錯誤都是有價值的。”數學課堂中出現的錯誤，有的是學生最初的思維展現，有的是學生最真的思維流露，教師應善于發現與捕捉學生的錯誤，點燃學生思維碰撞的火花，有效促進學生分析、比較、判斷、推理等思維能力，實現教學的最佳功效，不能漠視學生的錯誤抑或視而不見，錯失良機，需因勢利導，有目的、適度地展示與“放大”有價值的錯誤，組織與引導學生議錯、辨錯，聚焦知識的重點，突破學習的難點，有助于提升學生的思辨能力，促進數學思維的發展。

如一位老師在教學“不含括號的混合運算”時，讓學生嘗試計算350+180÷6×5后，先集體反饋正確的計算過程，接著展示收集到的典型的錯解，具體如下：

教者引導學生自主辨析錯誤，找出并劃出錯誤，想想哪兒出錯了，弄清錯因，緊扣混合運算的順序這個關鍵問題，讓學生在辨析錯誤、糾正錯誤的過程中，強化認識，加深印象。

再如運用商不變的規律計算被除數和除數末尾都有0的三位數除以兩位數時，一位老師呈現如下問題：幼兒園阿姨帶900元買洗衣液，如果每瓶50元，可以買多少瓶？如果每瓶40元，可以買多少瓶，還剩多少元？學生在解決第一個問題時，會用簡便方法計算900÷50 =18（瓶）。這里的第二個問題，既是鞏固商不變規律的簡便方法，同時引出本課的知識難點：運用商不變的規律計算被除數和除數末尾都有0的三位數除以兩位數時，余數究竟是多少？教者放手讓學生自主嘗試，有的學生豎式計算過程如下：900÷40=22（瓶）……2（元）

教者讓學生交流自己的計算過程，無形中“放大”錯誤，引發學生辨析：余數究竟是2還是20呢？這時，有學生提出可以用驗算的方法檢驗得數是否正確，教師讓學生“將錯就錯”進行驗算，發現22×40+2的得數不是900，而22×40+20=900，引導學生主動發現結果有錯，并進行錯誤的合理修正。接著，教者抓住關鍵知識點，進一步追問“為什么余數是20而不是2呢？”激活學生的數學思維，學生結合自己已有的認識，再次思考和辨析“商不變，余數變”，運用商不變的規律，自主解釋算理，進而知其然并知其所以然。

三、巧用錯思，以錯促學

杜威曾說過：“失敗是有教導性的，真正懂得思考的人，他從失敗和成功中學到的一樣多，甚至更多。”數學課堂教學過程中，引導學生反思錯誤與自我診斷，主動分析錯誤的深層次原因，是學生的數學思維不斷歷練、生長和提升的過程。教師不必急于指出學生的錯誤，催學生“被動”糾錯，不妨稍等片刻，把問題拋給學生，給學生多留一些自主究“錯”、反思的時間和空間，促使學生自我反省、剖析錯誤，在“思維風暴”中獲得更多的啟迪、頓悟，感悟數學思考的成功與快樂。教師應巧妙引導學生回顧與剖析自己的思維過程，找出錯誤原因，及時內化感悟新知，喚醒數學思維的重組，修正錯誤的認知，正確建構新知。

如一位老師教學“3的倍數的特征”，課一開始，老師就讓學生猜3的倍數有什么特征？有學生說看數的個位作判斷，有學生接著補充說“我們已經學過個位是0或5的數是5的倍數，個位是0、2、4、6、8的數是2的倍數。那么個位上是3、6、9的數是3的倍數”。因為學生在前一節課已經學習了“2和5的倍數的特征”，因此紛紛猜想“個位上是3、6、9的數是3的倍數”也就情有可原了，這是學生受到思維定式的影響，基于2和5倍數的特征影響到3的倍數特征的判斷。盡管有許多同學認同上述猜想，但也有同學發現猜想是錯的，并舉例23、26、29等數都不是3的倍數。這時，教者不置可否，而是把思考悟錯的機會留給學生，用期待的目光掃向學生，鼓勵他們積極動腦，然后做出評判。教者啟發學生思考：“既然不能從個位上猜想3的倍數的特征，那怎樣才能找出3的倍數的特征呢？”激發學生探究欲，燃起學生探究的熱情。學生已有探索規律的數學活動經驗，教者適時進行引導，讓學生再次經歷“猜想、舉例、驗證”的探究學習過程，學生通過大量舉例發現“這樣不行……”，繼而思考“為什么不行”？那么“怎樣才行……”繼而思考“為什么這樣行”？學生再通過舉例驗證，并注意進行及時的修正，最終探索出3的倍數的特征“各位上數字的和是3的倍數”。

總之，課堂教學是師生互動、生生互動的多維度動態過程，課堂教學是“一個生動活潑的、主動的和富有個性的過程”，在這一過程中，學生所學的數學知識是全新的，需要經歷一個從未知到已知的過程。因此課堂上會出現很多始料未及的錯誤。其實學生出錯是正常的，關鍵看我們怎樣來對待它，讓數學課堂變得更有意義，更有生命力，更精彩。學生的學習錯誤產生于學習活動中，亦可“消化”于學習活動中，作為教者的我們應因勢利導為學生創造發現錯誤、改正錯誤的機會，讓錯誤成為學生認知的“轉折點”，讓錯誤成為學生思維飛躍的“起跳板”，讓錯誤成為互學共進的“融合劑”。因此教師應以發掘資源的眼光看待錯誤，巧妙地利用錯誤甚至可以故意布設錯誤，夯實數學的課堂教學。為此，教學時，我們應巧用這些錯誤資源，引導學生進行探究，從而有效激活數學課堂。誠然，引導學生識錯、思錯、悟錯、糾錯，體現了學生對錯誤的再認識、再思考，這些有價值的錯誤均是教學中重要的生長點，值得巧妙用好、用實、用活。在學生自主診斷、修正錯誤后，教師及時引領學生分析梳理、總結概況，挖掘錯誤背后存在的數學問題，形成正確的數學概念思想方法等，有效提升數學思維能力。