驅動輪齒焊接徑向變形的優化與預測
趙永滿,付 威,侯曉曉,胡 斌
(1.石河子大學 機械電氣工程學院,新疆 石河子 832000;2.黃河交通學院 汽車工程系,鄭州 450062)
0 引言
驅動輪齒是覆土滾筒實現轉動和覆土的關鍵零件,工作時,驅動輪齒與鋪膜地面接觸,輪齒徑向長度影響地膜破壞率和種孔錯位率[1-2]。生產時,12個驅動輪齒通過焊接均勻分布在薄壁環形件表面,易產生徑向變形,影響輪齒徑向尺寸精度[2]。因此,有效優化和預測驅動輪齒焊接徑向變形,成為降低地膜破壞率和種孔錯位率的重要工作。
焊接數值模擬因不受物理條件制約、成本較低等優點受到學者熱衷,被驗證可靠有效[3-4]。焊接速度和焊接順序是影響焊接變形的兩個重要因素[4-5]。為此,本文以焊接速度和焊接順序為因子,驅動輪齒徑向變形為試驗指標,設計兩因素三水平正交試驗。借助Sysweld軟件模擬試驗方案,對結果進行方差分析,以優化試驗參數[6];同時,預估計最優方案下響應值上限。采用Minitab軟件建立焊接參數(焊接速度、焊接順序)與預測響應值(驅動輪齒徑向變形)的定量關系,實現焊接變形預測與控制,并通過現場試驗進行了驗證。
1 外緣圈和驅動輪齒焊接結構
焊接方式采用手工電弧焊,焊接電流200A、焊接電壓24V、焊絲牌號JQ-MG50-6(直徑16mm,長40mm)、保護氣體為CO2(氣體流量15~20L/min)。焊件包含外緣圈(內徑427mm,寬25mm,壁厚4mm,材料Q235)和驅動輪齒(直徑φ16mm,長45mm,材料Q235),12個驅動輪齒通過焊接均勻分布在外緣圈外表面,如圖1所示[7-8]。
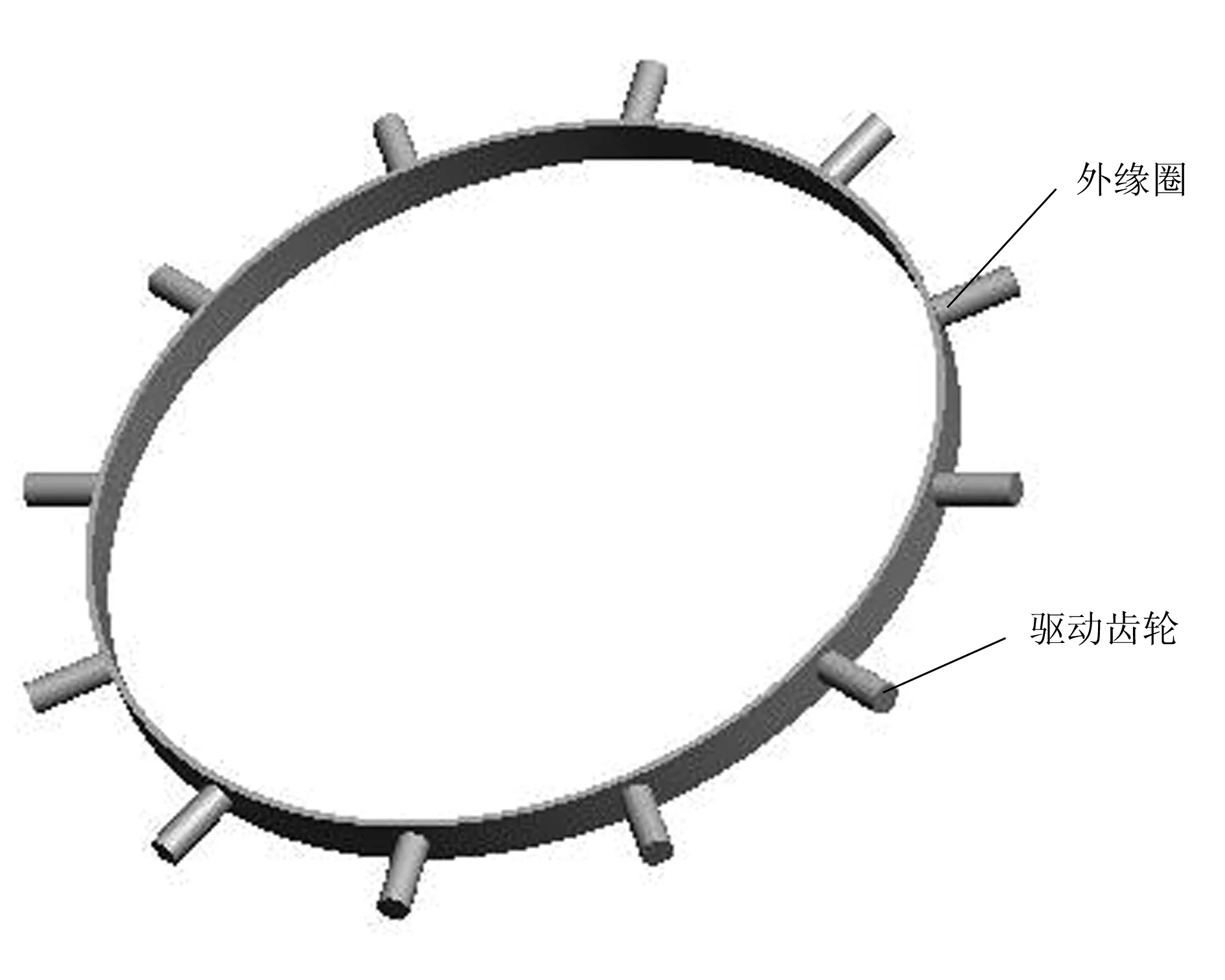
圖1 外緣圈和驅動輪齒結構Fig.1 Outer circle and drive gear teeth struc
2 試驗方法
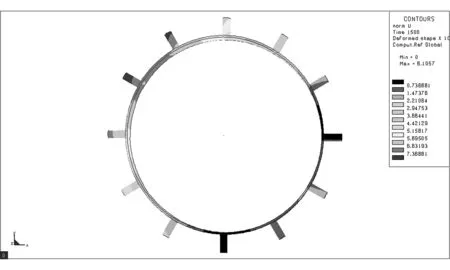
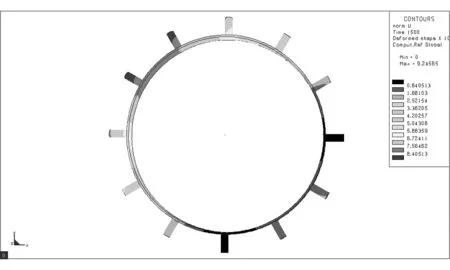
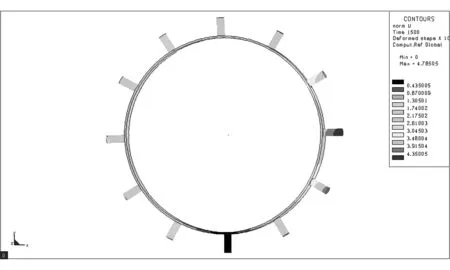
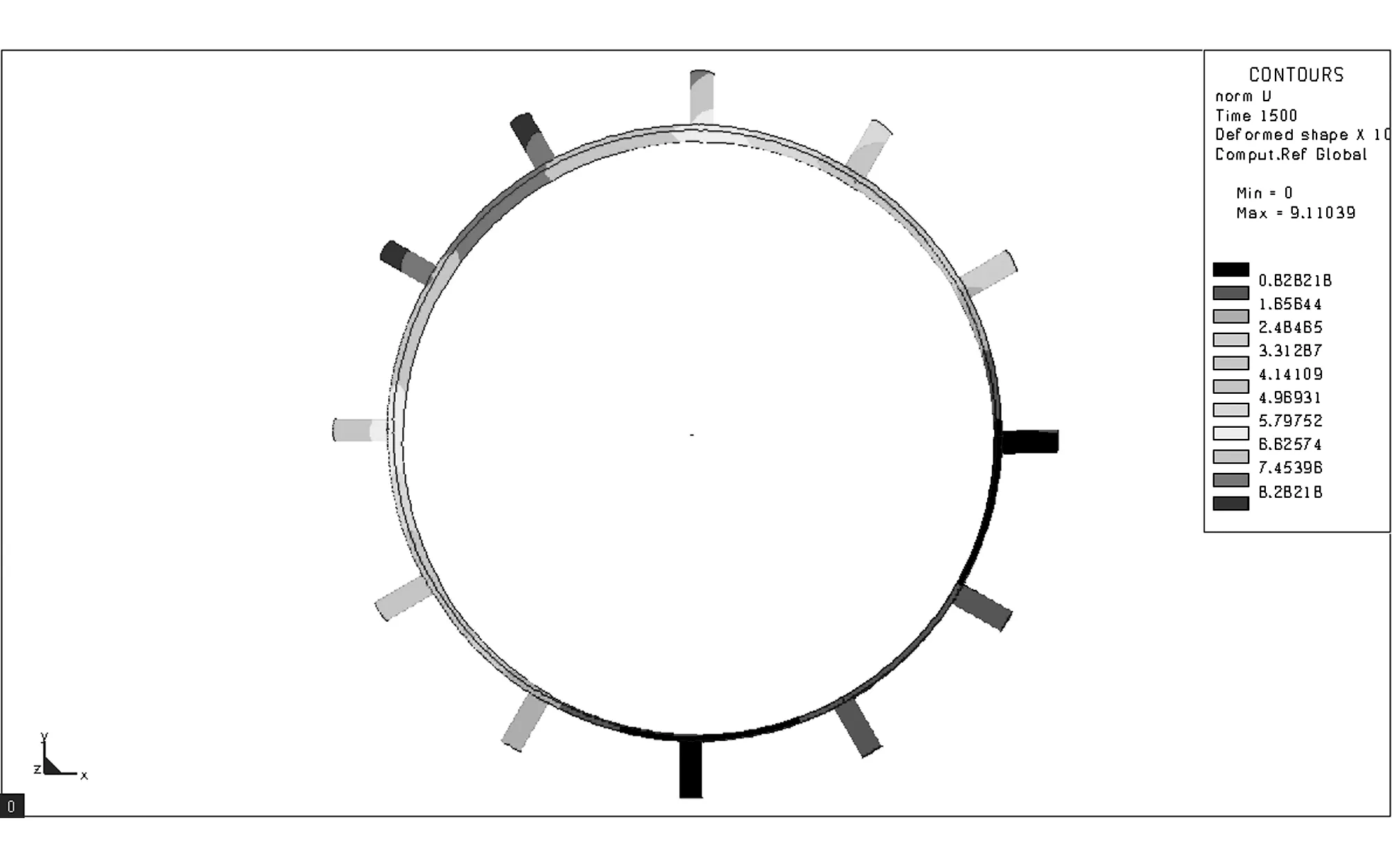
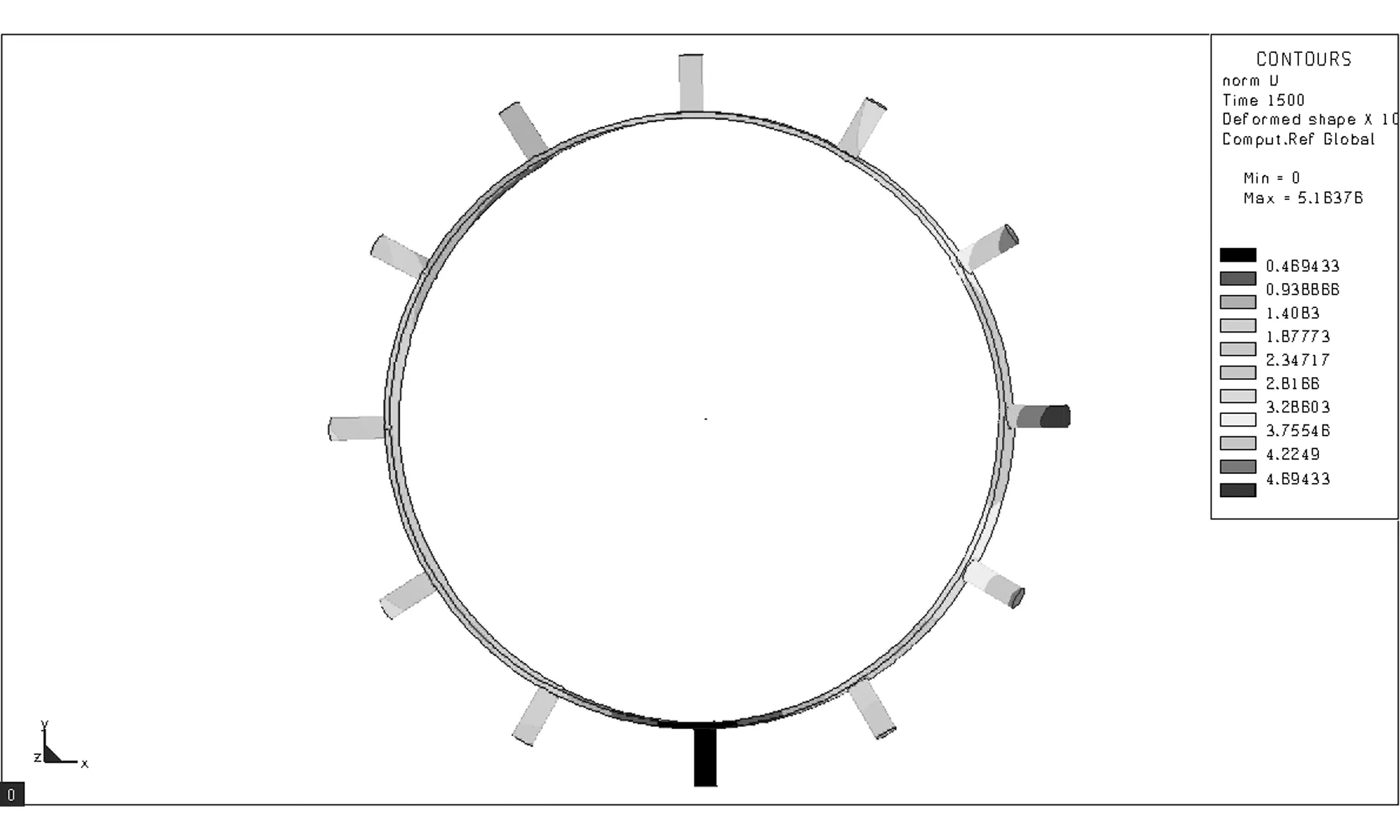
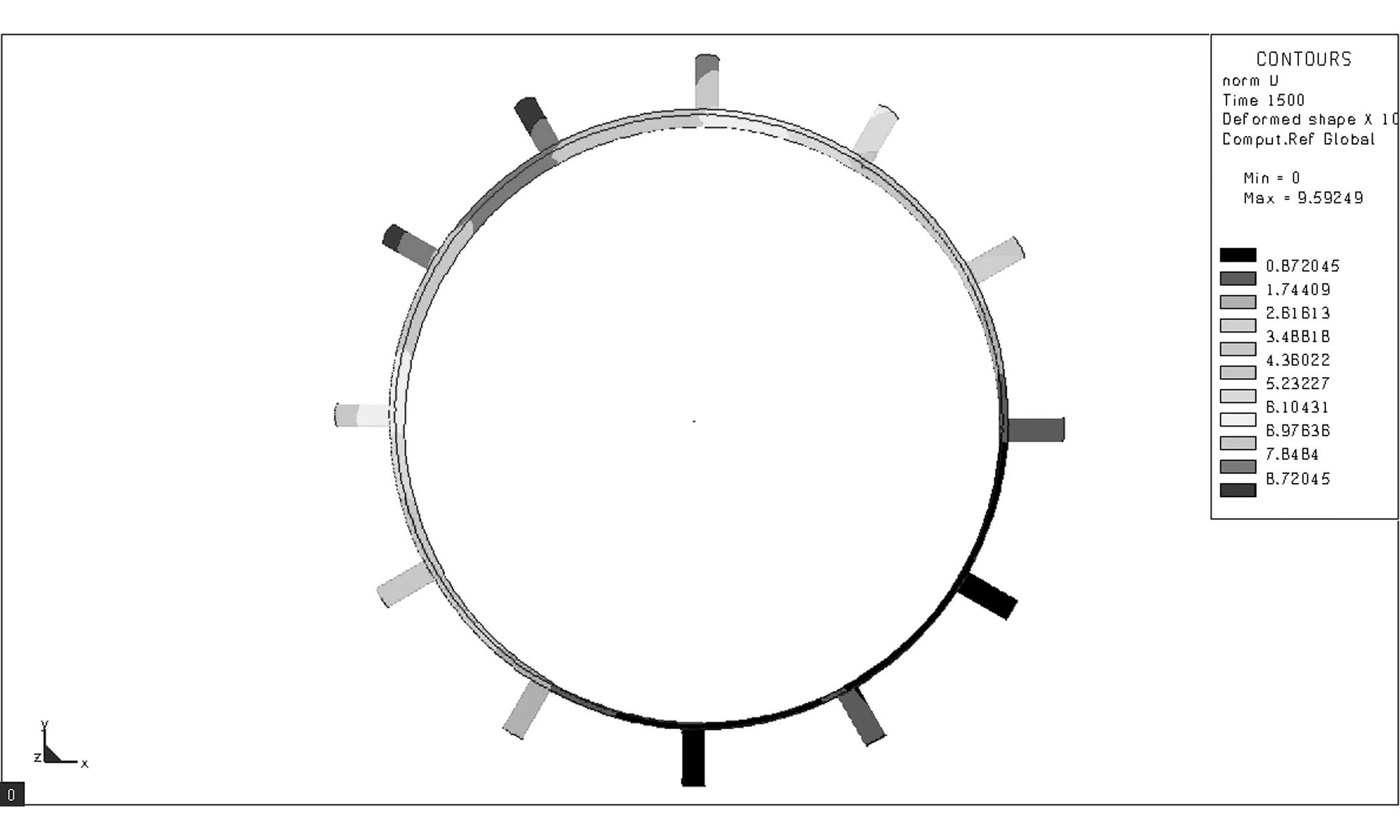
采用L9(34)正交表設計試驗方案,借助Sysweld軟件對各試驗號進行數值模擬,獲取分析結果[9]。Sysweld軟件部分模擬結果如圖2所示。對模擬結果進行方差分析,確定最優組合參數,估計最優組合下驅動輪齒徑向變形上限。采用多元二次回歸方程擬合焊接速度、焊接順序與驅動輪齒徑向變形的數學模型,預測不同焊接速度和焊接順序時的變形。試驗因素與水平設計如表1所示。其中,現場焊接速度為3.85mm/s,焊接順序為間斷跳焊II。試驗方案及結果如表2所示。
(a)
(b)
(c)
(d)
(e)
(f)
(g)
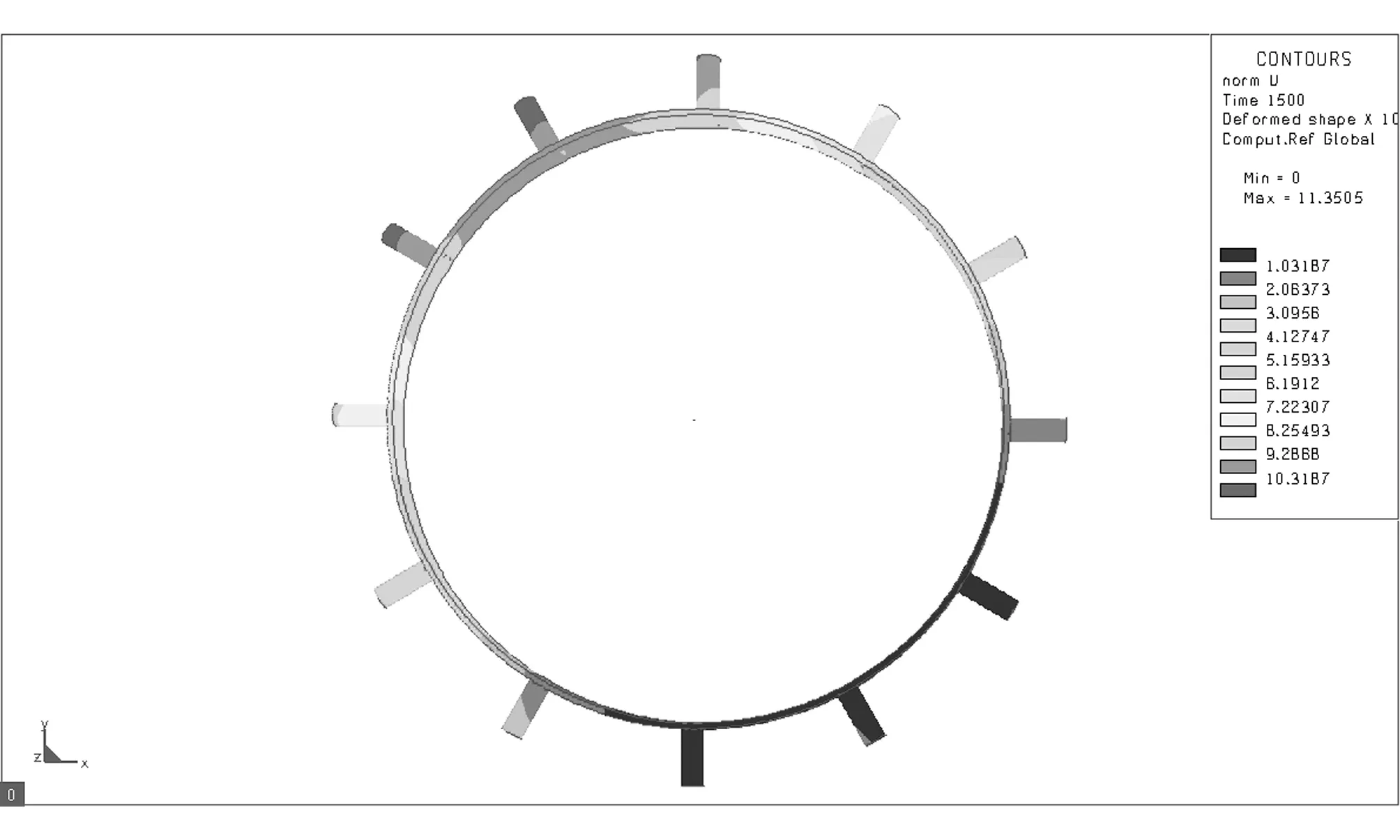
(h) 圖2 數值模擬結果Fig.2 Result of numerical simulation表1 焊接模擬因素水平表 Table 1 Factors and levels for welding simulation
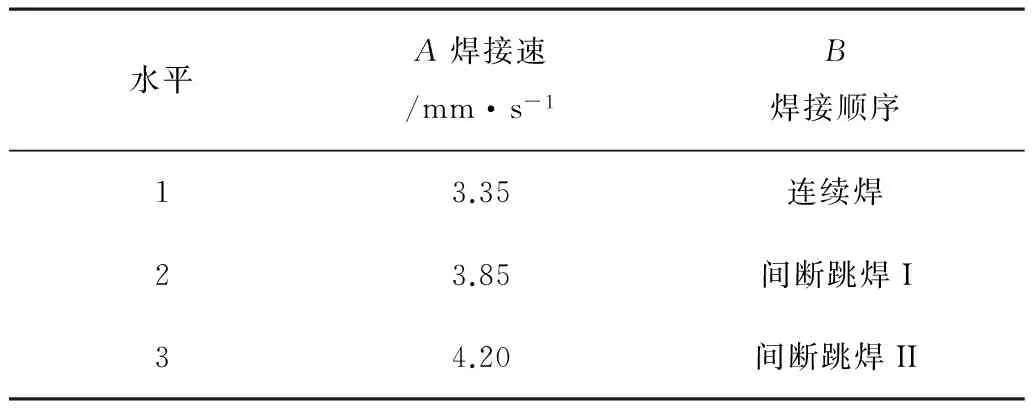
水平A焊接速/mm·s-1B焊接順序13.35連續焊23.85間斷跳焊I34.20間斷跳焊II
3種焊接順序分別見圖3中的(a)、(b)、(c)。
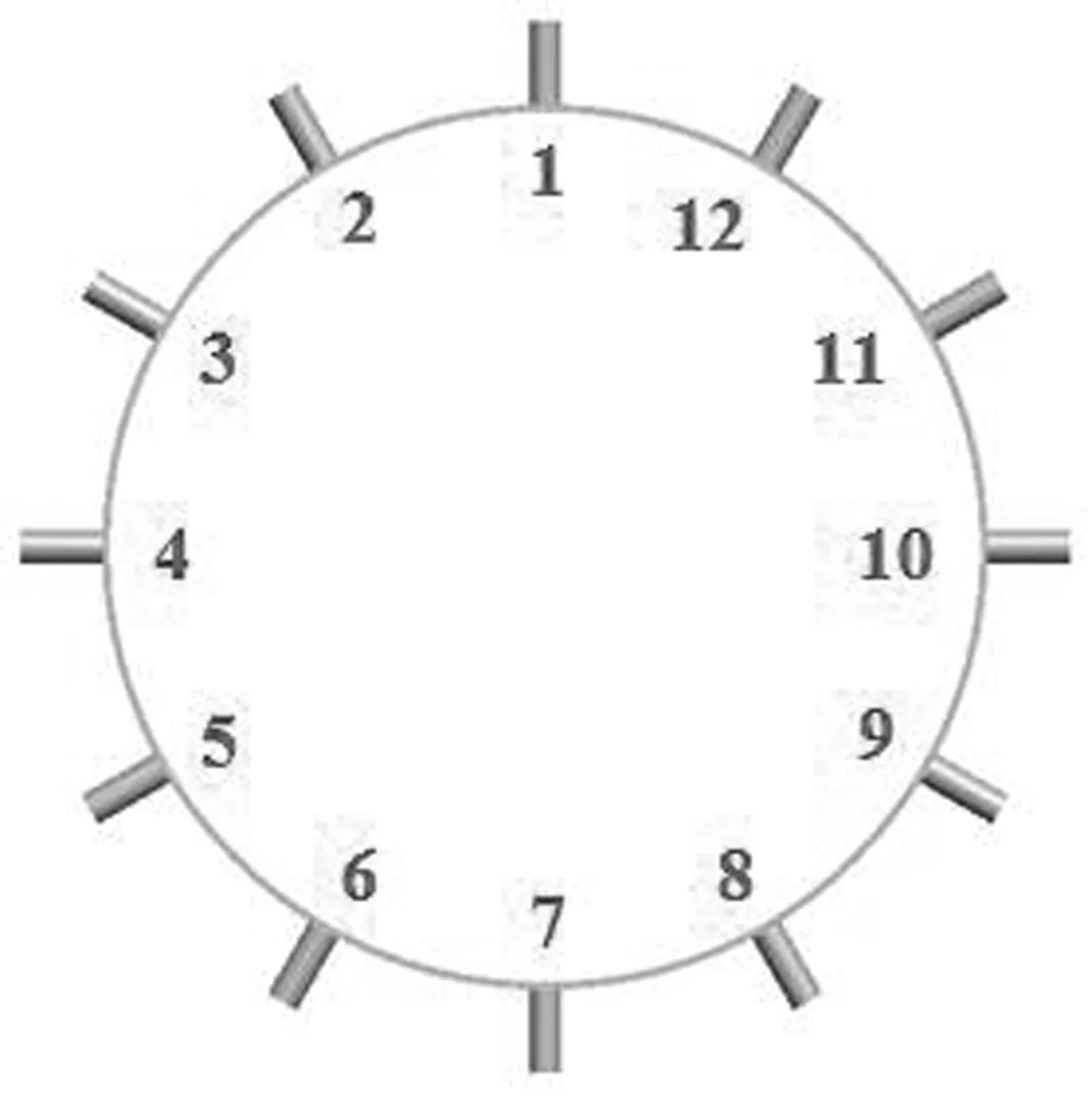
(a)連續焊
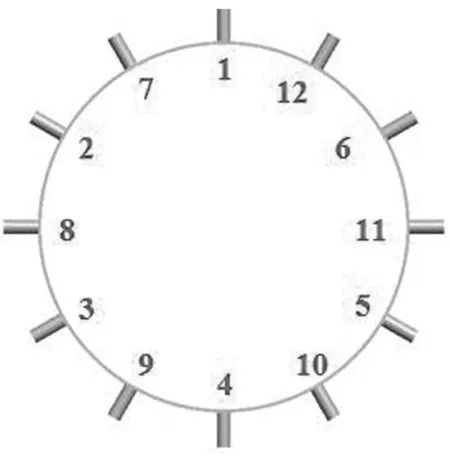
(b)間斷跳焊I
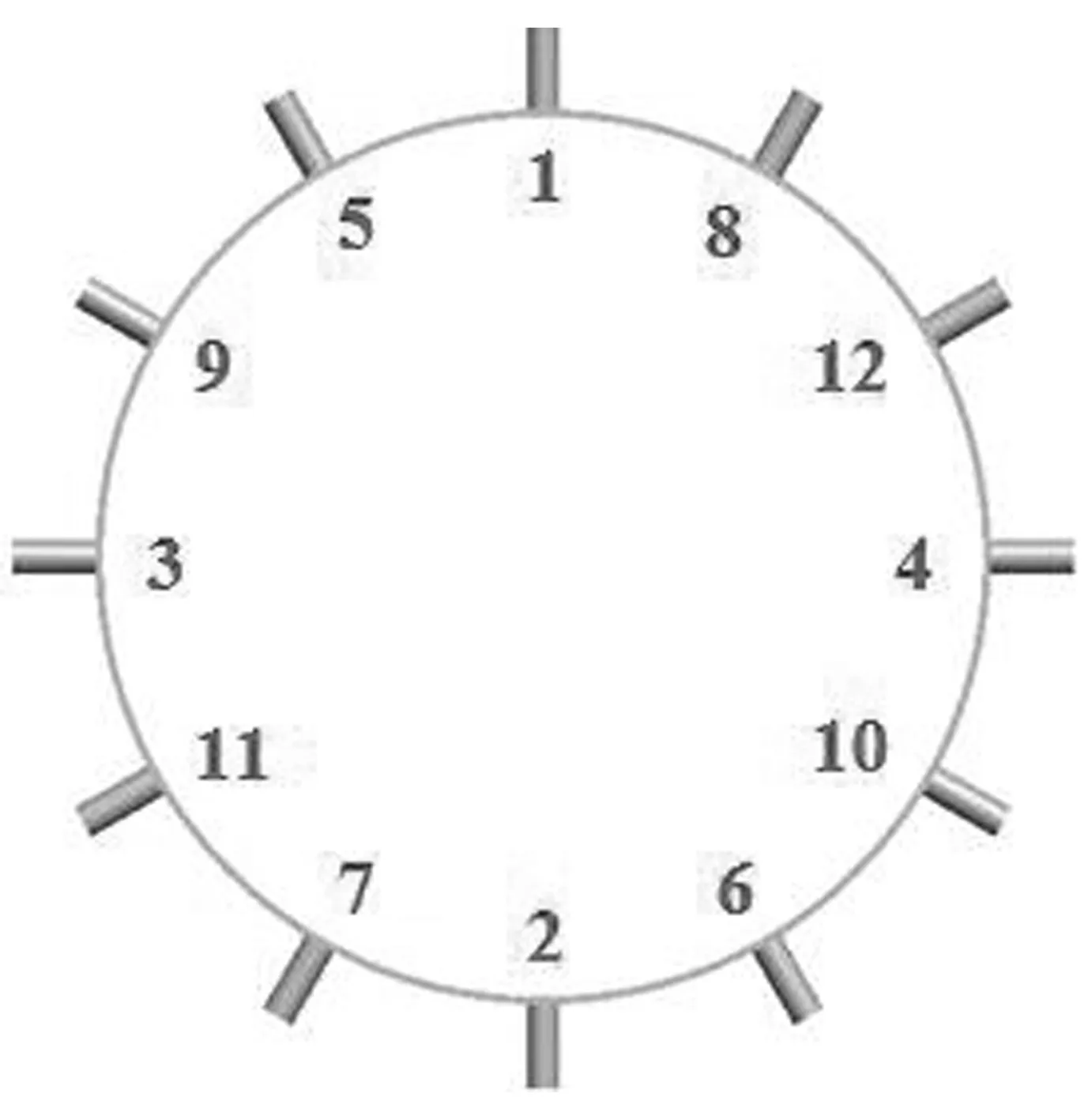
(c)間斷跳焊II 圖3 外緣圈和驅動輪齒焊接順序
3 試驗結果與分析
3.1 參數優化
對模擬結果進行方差分析,計算過程如表2所示。
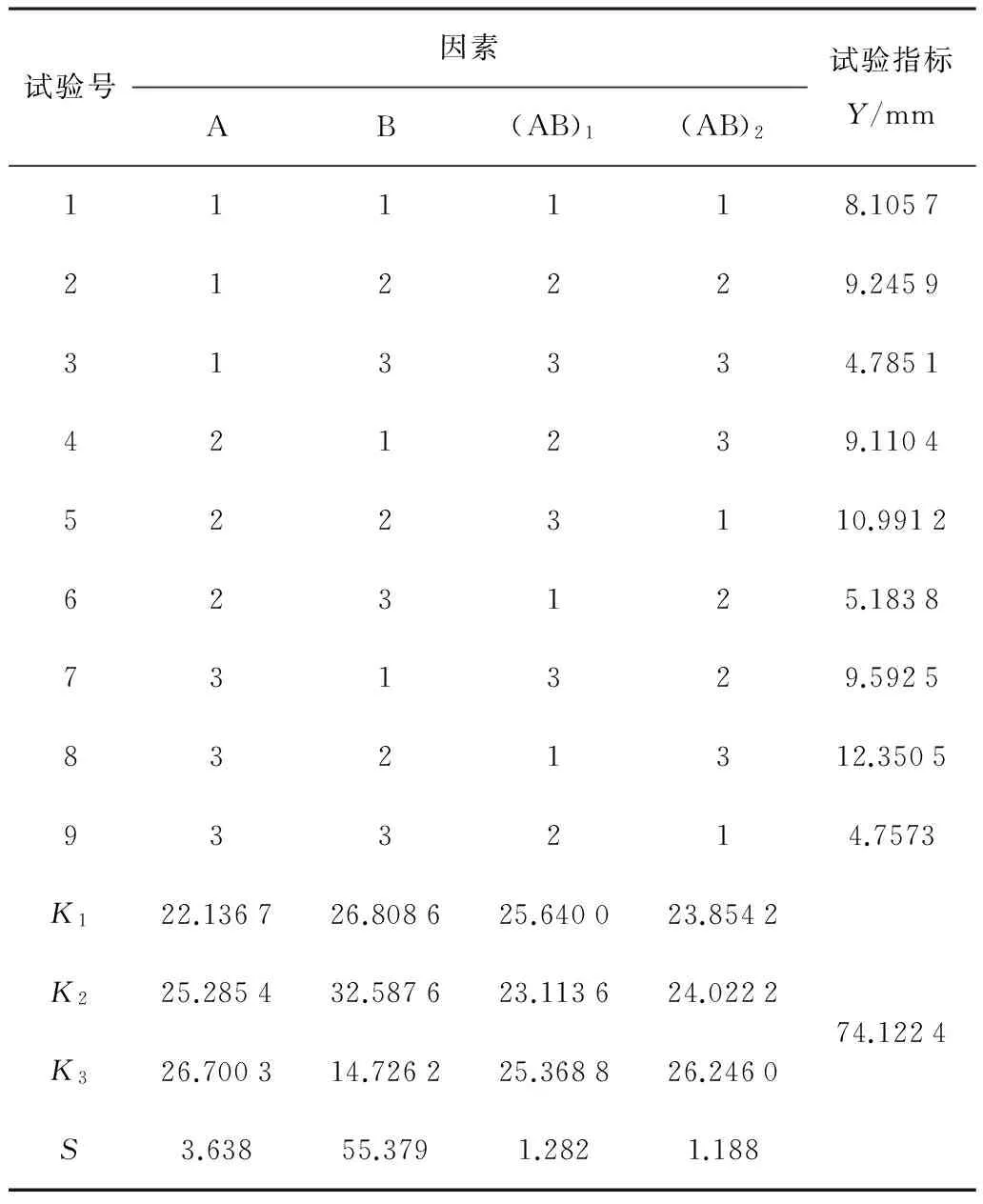
表2 試驗結果及計算Table 2 Test results and calculations
方差分析如表3所示。由表2可知:交互作用AB的離差平方和S值很小,可作為誤差項。驅動輪齒的變形越小越好,根據表2中各因素K值的最小值確定優水平,即A1B3。由表3可知:在95%置信度下,因素B(焊接順序)對徑向變形影響極顯著,因素A(焊接速度)有一定影響。因此,水平組合為A1B3。
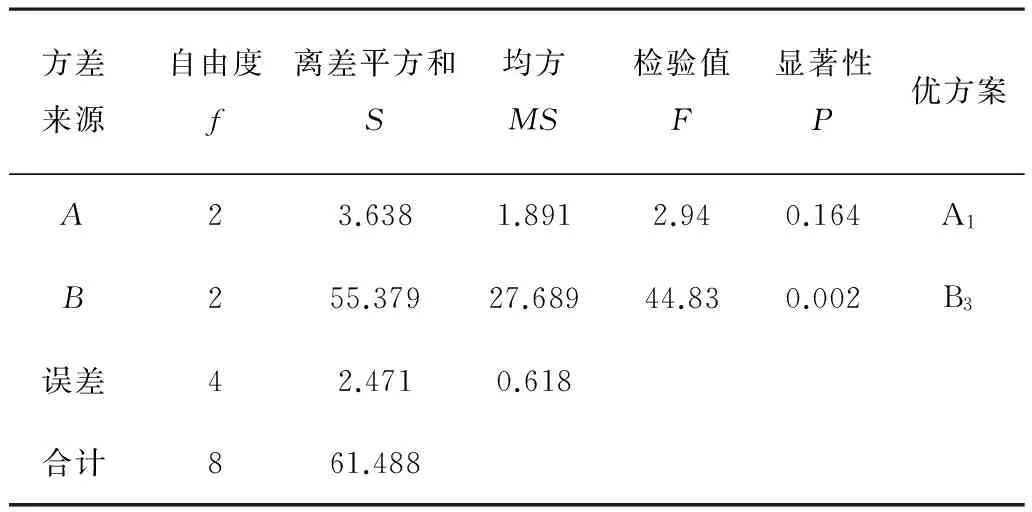
表3 方差分析表Table 3 Variance analysis of K
S=0.785 925,R-Sq=95.98%,R-Sq(調整)=91.96%。
3.2 最優組合下響應值上限估計
由方差分析和回歸方程確定的最優方案A1B3下變形為定值。但實際生產中,焊接干擾因素多樣且復雜,響應值產生一定浮動,有必要估計最優方案下響應值上限μ上。
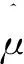

(1)
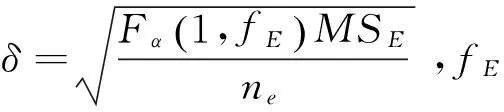
所以
(2)
(3)
所以

B為顯著因素,將因素A的離差平方和并入誤差,則新的誤差平方和SE、新的誤差自由度fE、nE分別為
SE'=SE+SA=6.109,fE'=fE+fA=6,ne=3
所以
在95%置信度下,F0.05(1,6)=5.99,則響應值上限為μ上=9.661 5,這表明生產中驅動輪齒徑向變形量不會大于9.661 5mm。
3.3 預測模型
采用Minitab軟件對模擬結果進行響應曲面回歸分析,剔除不顯著項。式(4)為以焊接速度和焊接順序為變量的驅動輪齒徑向變形的二元回歸模型(使用未編碼單位,焊接順序B取1、2、3),表4和表5分別為估計回歸系數和方差分析[10-11]。
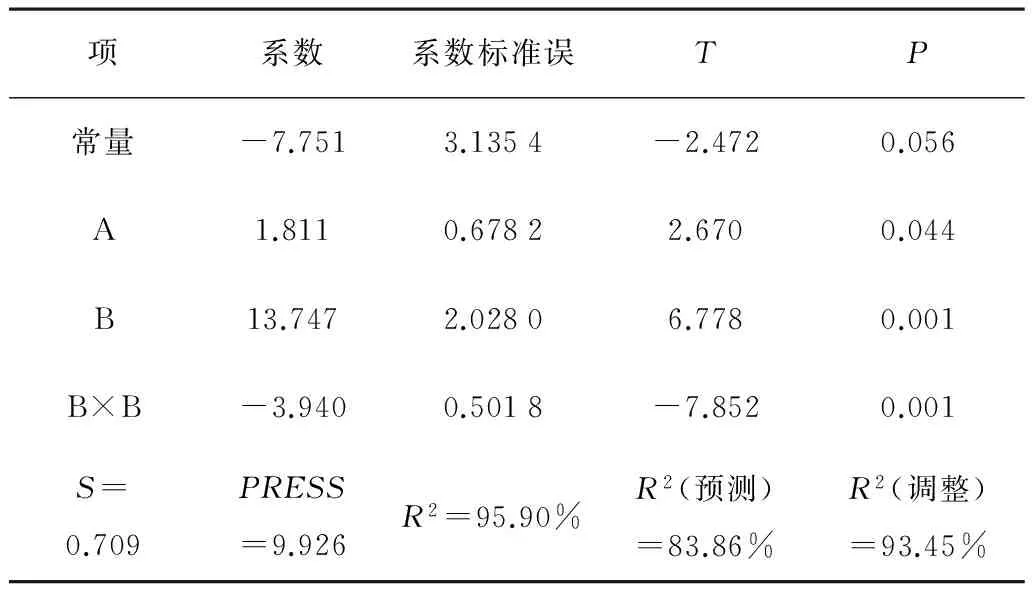
表4 Y的估計回歸系數Table 4 Estimated regression coefficients of Y

表5 Y的方差分析Table 5 The variance analysis of Y
分析表4:在95%置信度下,項B、B×B回歸系數高度顯著,A回歸系數顯著。R2=95.90%,調整R2=93.45%,表明曲面擬合得極好;預測R2(預測)=83.86%>80%,表明曲面方程能夠較好預測響應值Y;而且預測R2與R2、調整R2值相差較小,表明響應曲面沒有過度擬合。由表5可知:在95%的置信度下,回歸方程、一次項、二次項均高度顯著。綜上,該響應曲面擬合良好,響應曲面回歸方程為
Y=-7.751+1.811A+13.747B-3.940B×B
(4)
作等值線圖和3D曲面圖,如圖4所示。

(a) 等值線圖
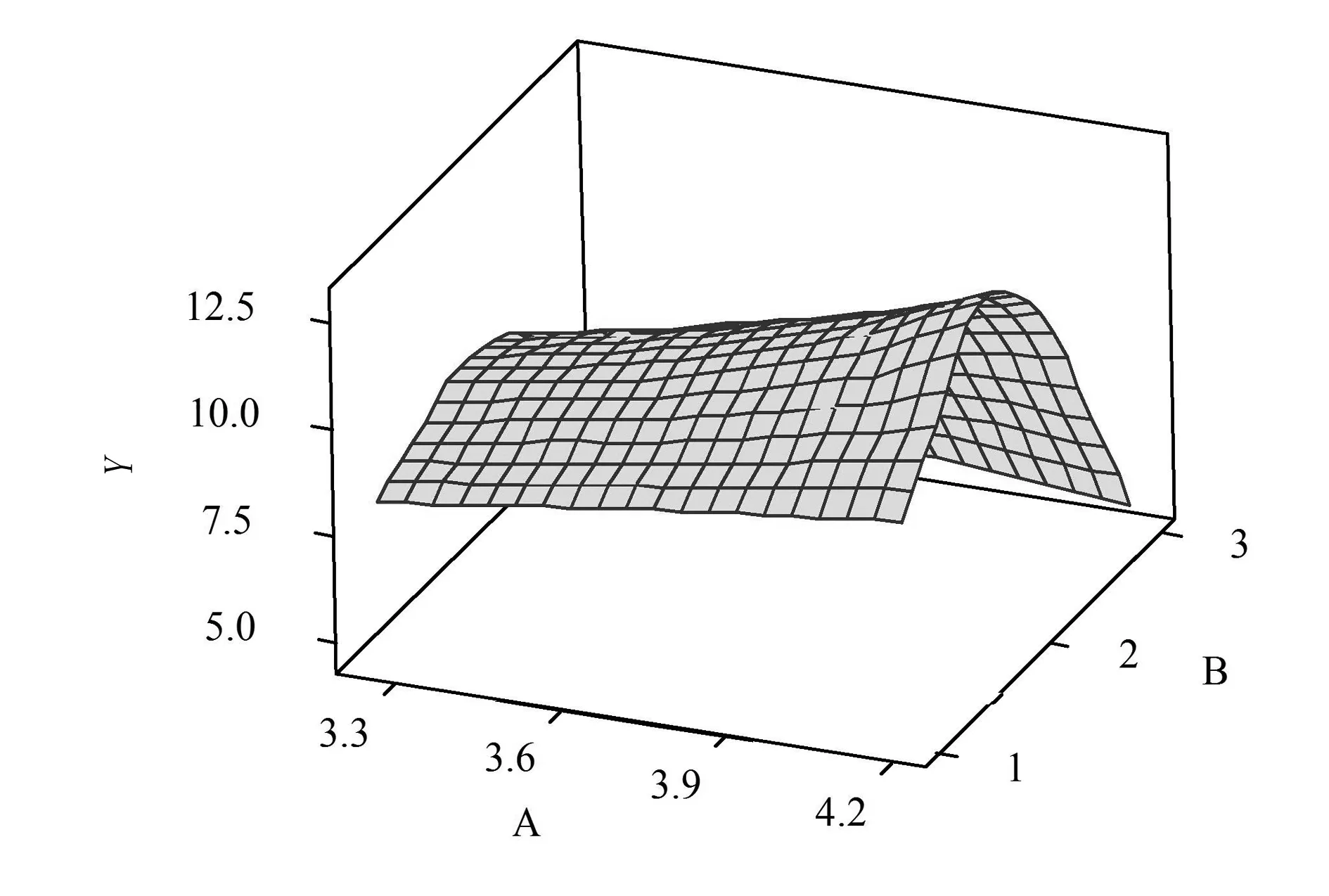
(b) 3D曲面圖 圖4 Y的等值線圖和3D曲面圖Fig.4 Contour map and surface plot of Y and B,A
分析等值線圖,與A方向相比,Y在B方向數值變化程度較大,B為主要因素。當B取B3、A取A1時,Y值最小。由3D曲面圖亦可得出該結論為焊接變形量Y的優搭配為A1B3,其與參數優化結果一致,可用來預測和控制焊接變形量Y。
3.4 試驗驗證
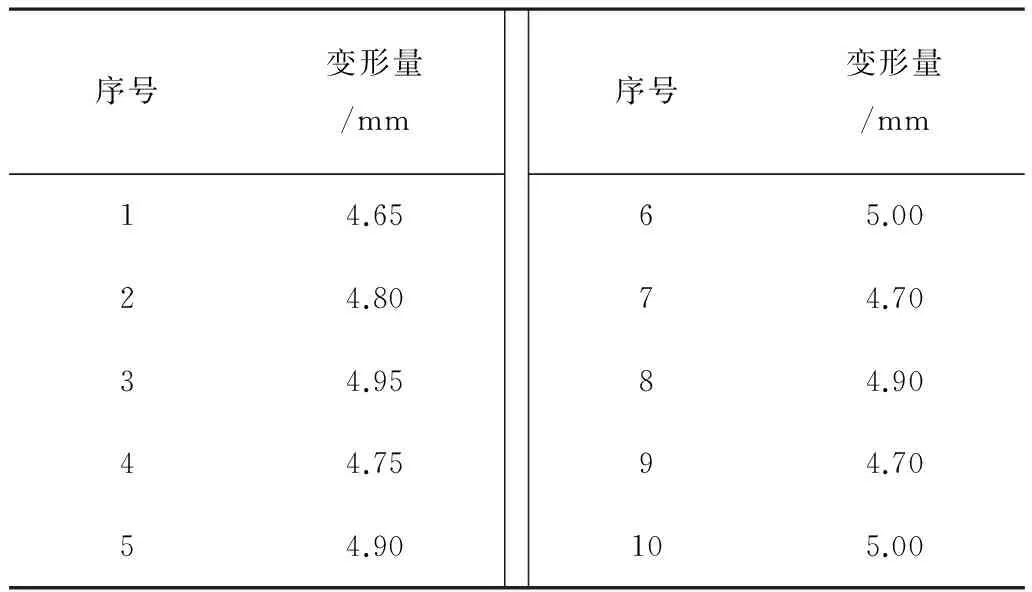
表6 優化前指標結果Table 6 Indicator results before optimizing
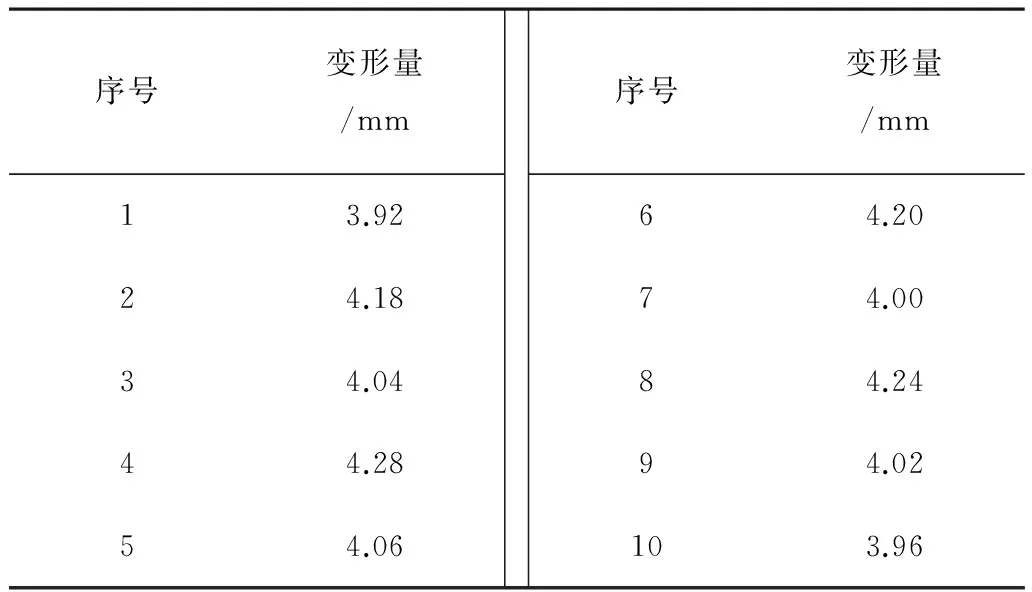
表7 優化后指標結果Table 7 Indicator results after optimizing
3.5 改進效果驗證
為了消除隨機誤差,將焊接速度定為4.20mm/s,采用圖3(c)中的焊接順序對外緣圈和驅動輪齒進行焊接,并抽取25組覆土滾筒成品進行左右半軸的同軸度測量,每組包含4個子組。制定控制圖,如圖5所示。
由圖5可知:圖中每個同軸度樣本值都處于控制線內,而且樣本的上控制線低于分析用控制圖(圖3~圖5)中的上控制線,表明經過過程改進后,覆土滾筒生產過程處于穩態,覆土滾筒左右半軸同軸度能夠滿足生產技術要求(低于500mm)。因此,將分析用控制圖轉化為控制用控制圖以判斷覆土滾筒后期生產過程穩定性。
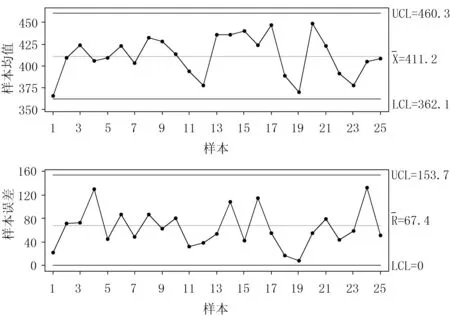
圖5 控制用控制圖Fig.5 The controlling control chart
4 結論
1)基于正交試驗方案確定降低驅動輪齒焊接變形的最優組合參數:焊接速度4.20mm/s、焊接順序間斷跳焊Ⅱ,焊接順序對變形影響高度顯著。最優組合參數下變形量的估計上μ上=9.661 5mm。
2)基于響應曲面法建立驅動輪齒焊接變形與焊接速度和焊接順序的多元二次回歸數學模型顯著性高,且擬合極好。
3)最優方案試驗表明:平均變形量降低了18.22%,測量值均未超過估計上限;測量值和預測值的絕對誤差小于5%,預測模型可靠。
[1] 陳學庚,趙巖.棉花雙膜覆蓋精量播種機的研制[J].農業工程學報,2010,26(4):38-41.
[2] 董文超,陸善平,李殿中.焊接順序對大型薄板裝甲鋼結構變形的影響[J].焊接學報,2015,36(7):43-46.
[3] 郭廣飛,王勇,韓濤.天然氣管道在役焊接徑向變形數值模擬[J].焊接學報,2014,35(12):55-58.
[4] 李江飛,齊海波,任德亮,等.薄壁多焊縫復雜構件焊接過程的數值模擬[J].焊接學報,2015,36(1):87-90.
[5] 張國棟,薛吉林,周昌玉.基于正交試驗設計的高溫管道焊接工藝優化[J].焊接學報,2008,29(11):54-56.
[6] 呂小蓮,胡志超,張會娟,等.氣吸式花生膜上精量穴播輪田間作業性能測試[J].西北農林科技大學學報,2014,42(6):213-218.
[7] 李曉延,武傳松,李午申.中國焊接制造領域學科發展研究[J].機械工程學報,2012,48(6):19-31.
[8] 范玉濱,楊然兵,柴恒輝,等.膜上苗帶覆土裝置設計與實驗研究[J].中國農機化學報,2014,32(5):5-8.
[9] 朱寧帥,劉元義.基于遺傳算法的葉輪的優化設計[J].中國農機化學報,2014,35(4):107-110.
[10] 高國華,馮天翔,李福.斜入式穴盤苗移栽手抓工作參數優化及實驗驗證[J].農業機械學報,2015,31(24):16-22.
[11] 丁素明,薛新宇,方金豹,等.手持式風送授粉機工作參數優化與實驗[J].農業工程學報,2015,31(8):68-75.
[12] 陳魁.試驗設計與分析[M].北京:清華大學出版社,1996.

