基于改進型灰色馬爾可夫模型的公路貨運價格預測

湯銀英，李龍，秦陽

（1. 西南交通大學，交通運輸與物流學院，成都610031；2. 綜合交通運輸智能化國家地方聯合工程實驗室，成都610031）

0 引 言

近幾年隨著公路運輸在我國運輸市場中占有的份額不斷增大，公路貨運對我國物流行業的影響也越發深遠。公路貨物運輸價格是反映公路貨運市場供需關系的“晴雨表”，也是合理配置公路貨運市場資源的基礎性手段[1]。探究公路貨運價格變化規律，把握運價變化趨勢，對于政府調節公路貨運市場發展及運輸企業適應市場變化都有著重要意義。

公路運輸市場化程度較高，其貨運價格隨市場波動變化的頻度與幅度都比較大，這使得公路貨運價格預測工作較為困難，預測精度普遍不高。另外，由于公路貨運價格受到市場供需狀況、油價、政府相關政策、車輛保有量等多種因素共同影響，而這些影響因素的信息獲取困難較大，所以基于因果關系的預測方法很難適用。研究發現一些傳統預測方法諸如回歸分析法、灰色模型等在進行公路貨運價格預測時雖然可以克服影響因素信息缺乏的困難，但是存在對歷史數據有用信息提取不足，對貨運價格波動曲線的擬合程度不高等缺點，使得預測結果很不理想[2]。灰色馬爾可夫組合模型能夠針對信息缺失且短期波動劇烈的時間序列數據進行預測，并且預測效果良好，但其預測精度仍存在進一步提升的空間。因此本文對灰色馬爾可夫模型加以改進，提高了公路貨運價格數據的預測精度[3]。

1 灰色馬爾可夫組合模型基本思想

公路貨運系統中影響公路貨運價格的因素眾多，但由于人們的認知能力有限，難以合理確定公路貨運價格變動的上漲因素與下降因素，以及引起運價變化的主要因素與次要因素等。因此，可以將公路貨運系統視為一個沒有清晰因果關系的、信息不完全的灰色系統，進而用灰色理論加以研究。灰色理論中的單序列一階線性微分方程預測模型（也稱為灰色GM（1，1）模型）無需從影響公路貨運價格的眾多因素中進行主要因素的比選，也無需對各個影響因素單獨進行數據的調查和分析，因此適用于信息不全的數據序列的預測，并且對歷史數據中存在的長期增長（或減少）的趨勢量（即殘差）能進行較為精確的預測，因而具有簡單適用的特點。但是灰色GM（1，1）預測模型要求對歷史數據累加后生成的數列具有指數規律，而公路貨運價格波動頻率和幅度都比較大，采用單一的GM（1，1）預測模型則會自動過濾掉這種隨機性波動，無法對歷史數據中的有用信息進行充分提取[4-6]。

另外，公路貨運系統是一個動態的系統，貨運價格作為公路貨運這一動態系統的特征量，它的變化會呈現出隨機過程的特點，而馬爾可夫鏈可描述這種具有隨機波動特點的動態過程。與灰色GM（1，1）模型相比較而言，馬爾可夫過程則可以實現對歷史數據中的狀態轉移信息進行充分的提取，并且通過狀態轉移概率矩陣來體現系統的內在規律性，適用于隨機波動性較大的非平穩數據序列的預測。

將上述兩種模型結合后形成了灰色馬爾可夫模型，采用灰色預測模型來揭示公路貨運價格變化的總體趨勢，然后采用馬爾可夫鏈來確定不同狀態間的轉移規律，從而使得灰色馬爾可夫模型兼具二者的特點，對波動性較強的數據的預測更加精準[7-9]。

2 構建改進型灰色馬爾可夫模型

在改進型灰色馬爾可夫建模過程中，首先，建立灰色GM（1，1）模型進行預測，將灰色預測結果作為馬爾可夫過程的狀態區間劃分的依據；然后，計算出各狀態區間的轉移概率，構建狀態轉移概率矩陣，得出灰色馬爾可夫模型以及改進型灰色馬爾可夫模型預測結果；最后，進行預測精度檢驗，以便于評定預測模型的預測效果。

2.1 建立灰色GM（1，1）模型

（1）對歷史數據進行一階累加，生成累加數列：

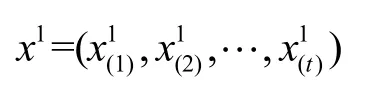
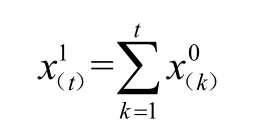
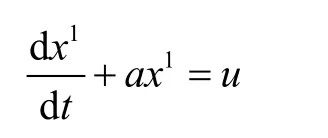
其中，a、u分別為發展系數和灰色作用量，a的有效區間為（-2，2）。

（3）對累加生成數據做均值生成向量B與常數向量Yn，即

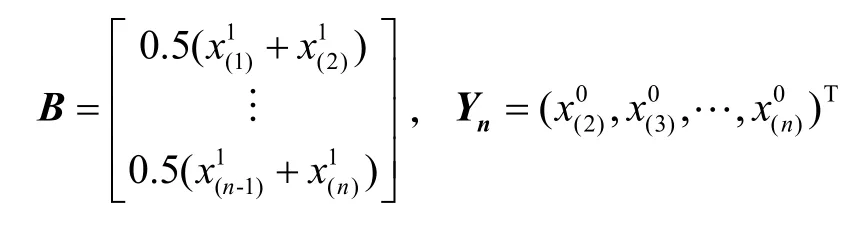
（4）記a，u構成的矩陣為，利用最小二乘法求解灰參數，則

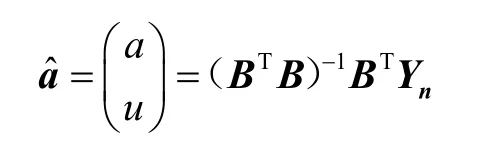
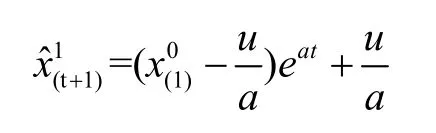
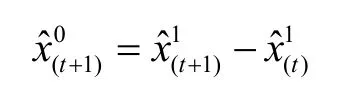
2.2 建立灰色馬爾可夫模型

（1）狀態區間劃分

以公路貨運價格實際值與GM（1，1）模型預測值的相對比值p的取值范圍s為依據，進行馬爾可夫狀態區間的劃分，將p的取值范圍等長度劃分為n個區間，得到n+1個狀態分界值s=(s1,s2,…,sn+1)，其中n為狀態區間個數。

則狀態區間Ei具體劃分如下：

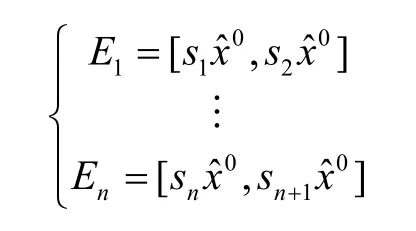
（2）構建k步狀態轉移概率矩陣

數據序列由狀態Ei經過m步轉移到狀態Ej的概率記為p(k)ij，則

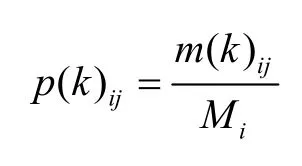
記k步狀態轉移概率矩陣為p(k)，則

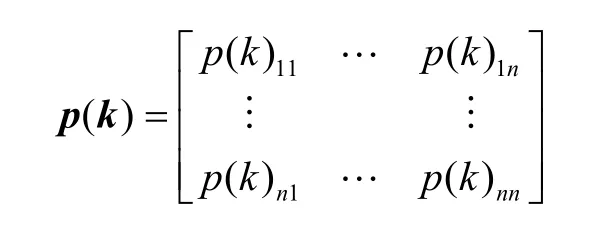
利用狀態k步轉移概率矩陣p(k)，可以計算出轉移至狀態區間Ei=(E1,E2,…,En)的對應概率為Pi=(P1,P2,…,Pn)，將Pmax所對應的狀態區間Emax作為最后所處的狀態區間。

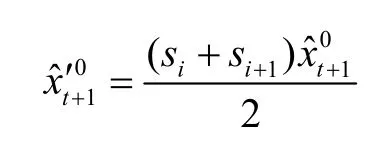
2.3 建立改進型灰色馬爾可夫模型

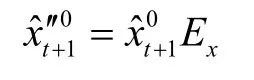
其中，狀態轉移期望：

其次，個人考核是關鍵。以團隊為單位進行考核雖為重點，但如果將它作為課程考核的唯一標準，則有失公平，可能對個人學習積極性、團隊的學習態度和協作精神產生負面影響。

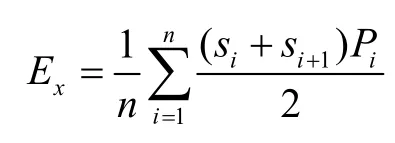
2.4 預測精度判定

最后需要對預測結果分別進行精度評定，評定步驟如下：

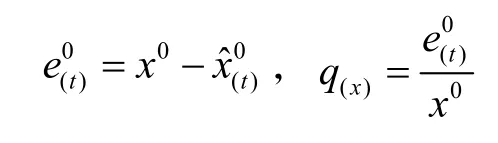
（2）對照精度檢驗表（見表1），進行預測精度評定。

表1 精度檢驗對照表Tab.1 Model precision table

3 公路貨運價格預測實證分析

本文以成都至南昌的公路運輸周價格作為研究對象，采集了該通道上2015年8月5日至2016年9月28日期間59周的公路運輸周價格數據，選擇前46周的數據作為原始數據，對該通道2016年7月6日至2016年9月28日期間13周的公路運輸周價格進行預測，見表2。

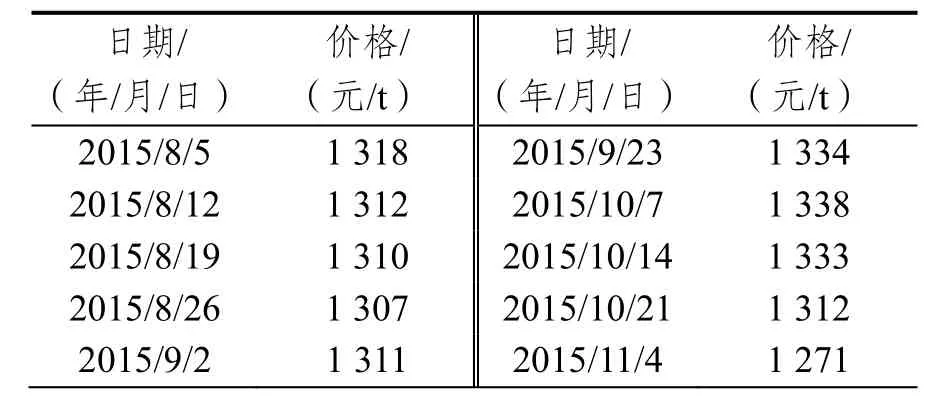
表2 成都至南昌公路運輸周價格表Tab.2 Highway freight transportation price from Chengdu to Nanchang

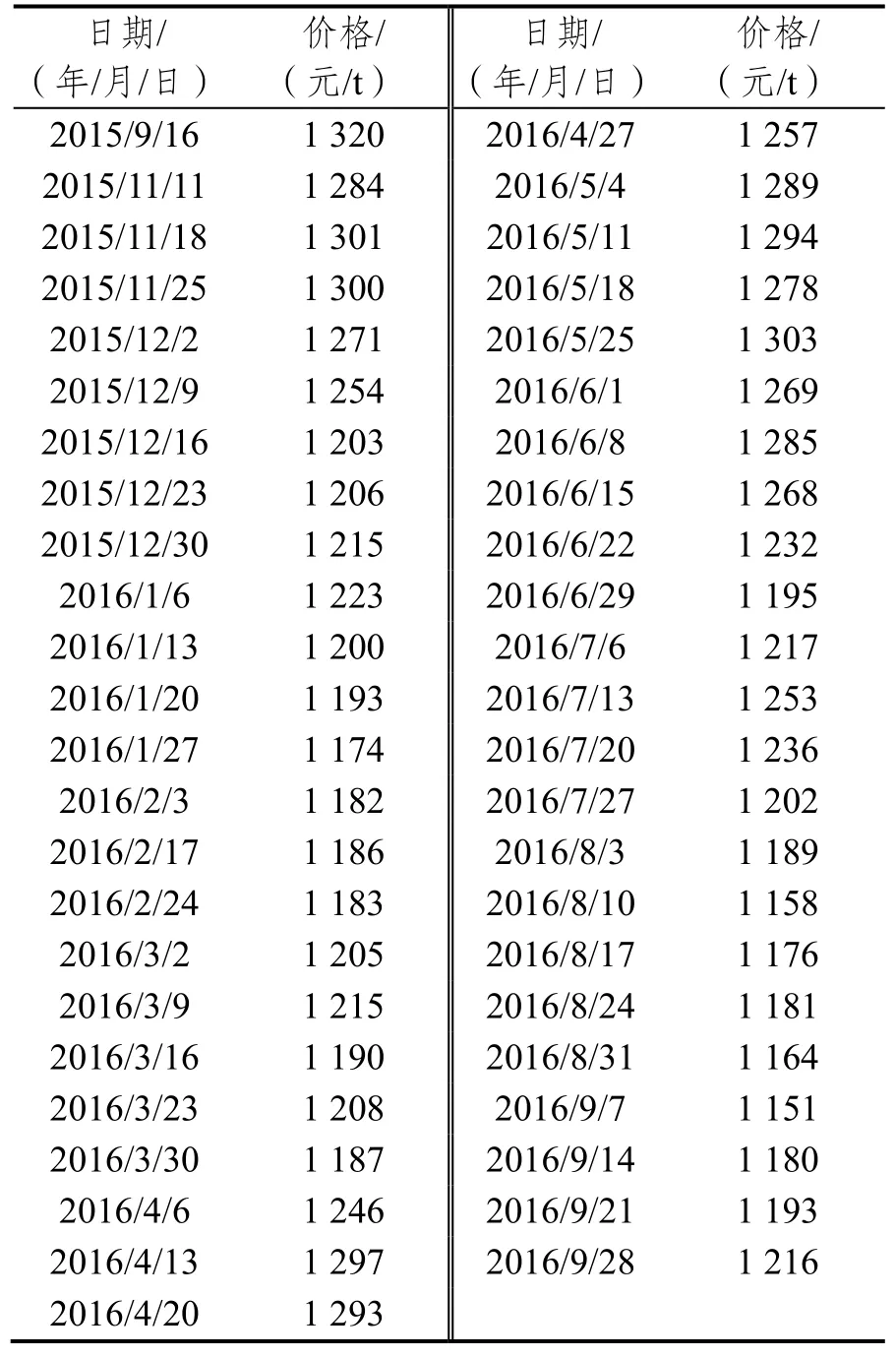
續表2

3.1 進行灰色GM（1，1）模型預測

建立原始序列：

x0=(1223 ,1200,…,1195)，n=25

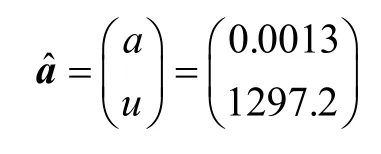
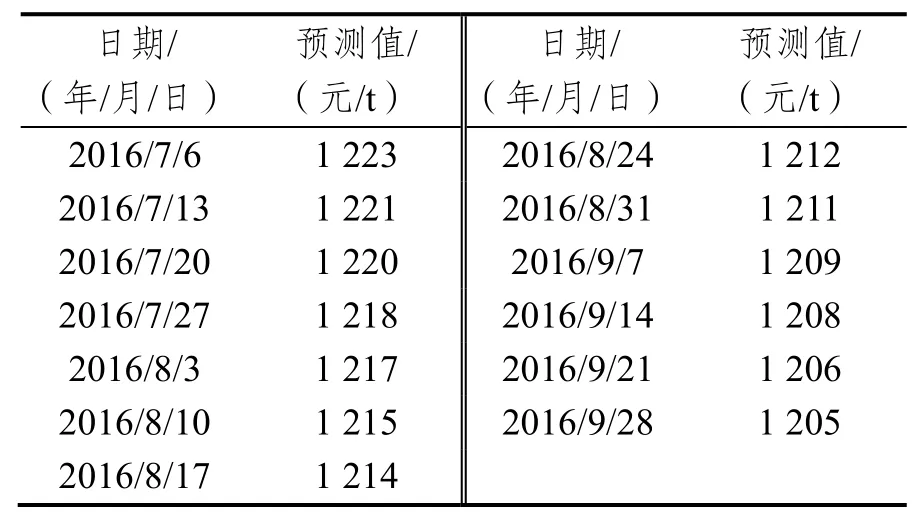
表3 灰色GM（1，1）模型預測值Tab.3 The GM（1，1）prediction results

3.2 進行灰色馬爾可夫模型預測

（1）確定狀態區間

公路貨運價格實際值與GM（1，1）模型預測值的相對比值p的取值范圍為s=[0.92，1.12]，等長度劃分為四個區間，則各個狀態對應的區間分布如表4所示。

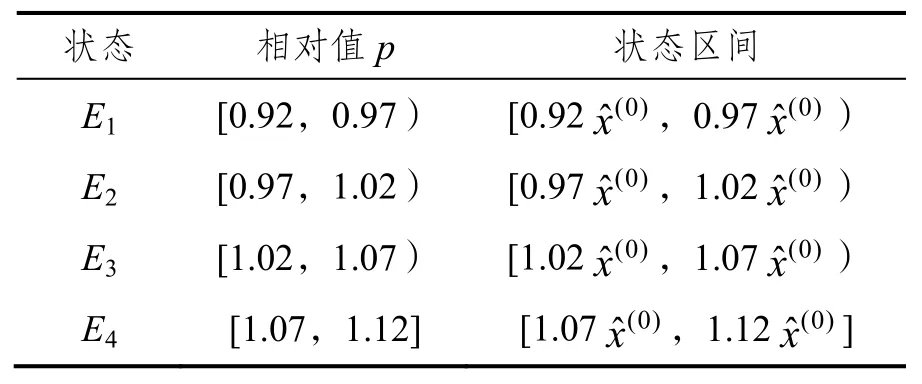
表4 狀態區間劃分表Tab.4 Feasible state ranges

（2）計算狀態轉移概率矩陣

分別計算k（k≤4）步轉移矩陣：

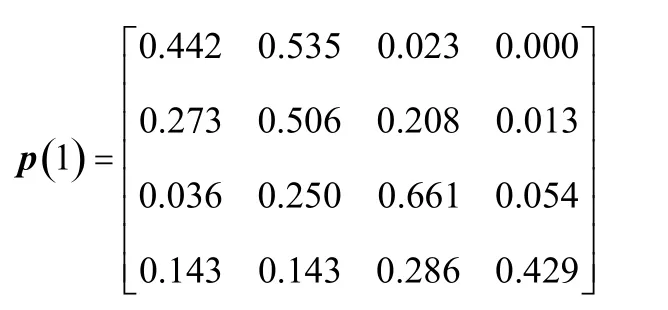
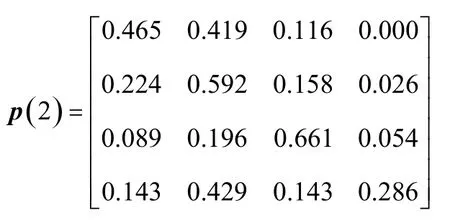
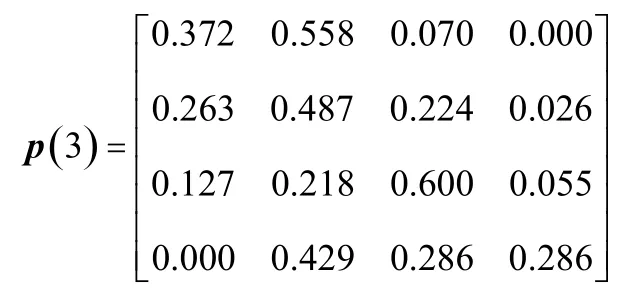
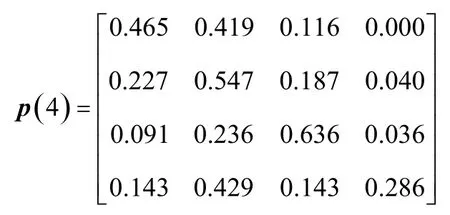
以2016年7月6日成都至南昌的公路貨運價格為例進行預測，狀態轉移區間預測過程如表5所示。

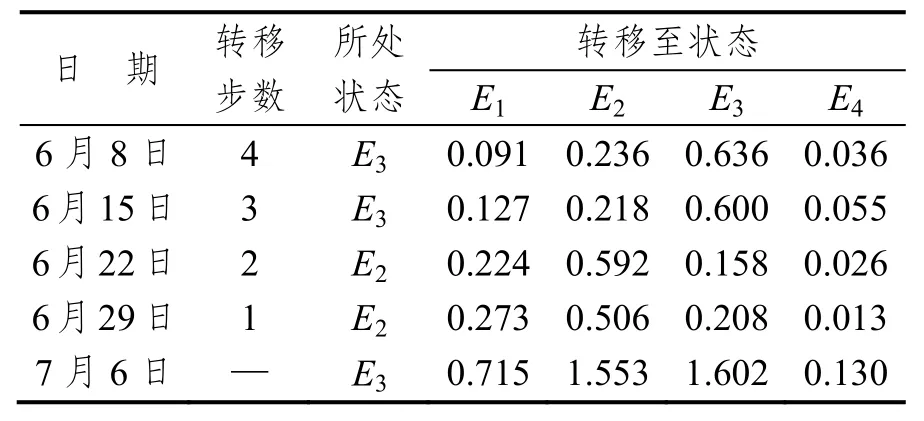
表5 狀態區間預測計算表Tab.5 State transition table (Gray-Markov)

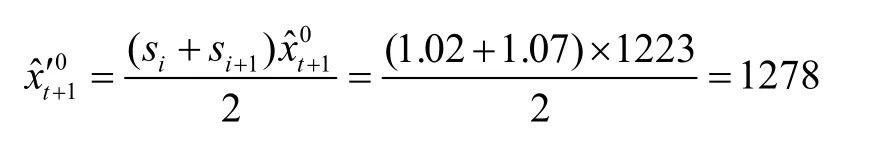
最終預測結果見表6。

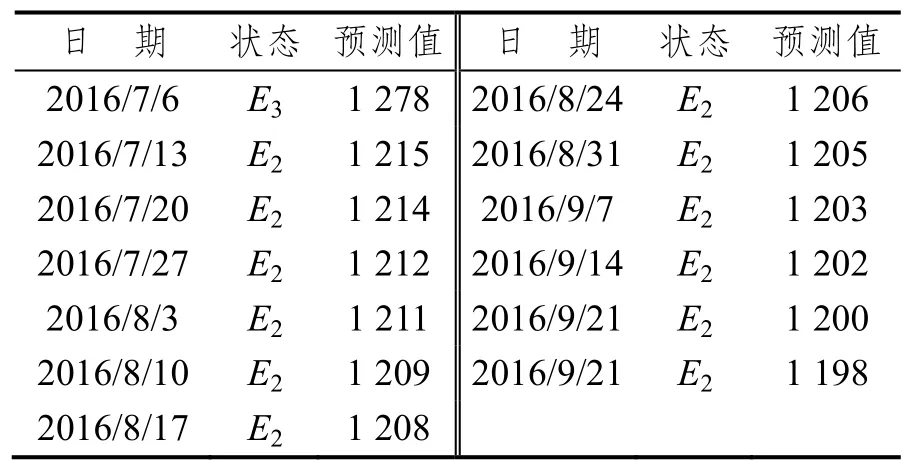
表6 灰色馬爾可夫模型預測值Tab.6 The Gray-Markov predictions

3.3 改進型灰色馬爾可夫模型預測值

同樣，以2016年7月6日的成都至南昌的公路貨運價格為例進行預測，預測結果如表7所示。

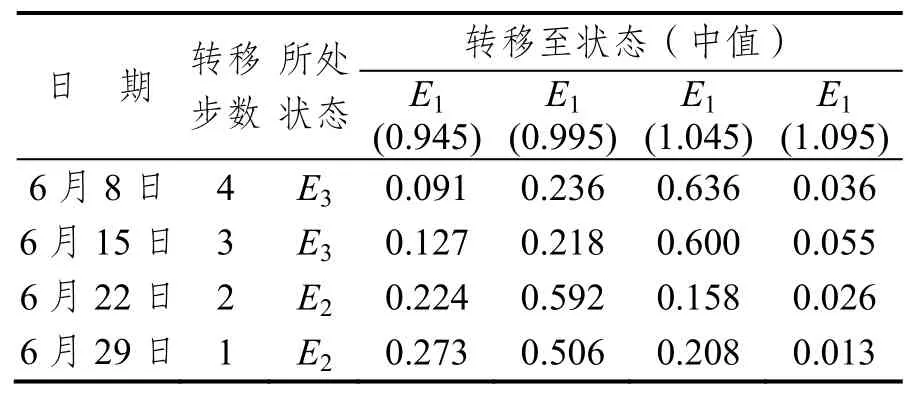
表7 狀態區間轉移期望計算表Tab.7 State transition table (improved Gray-Markov)

表中，

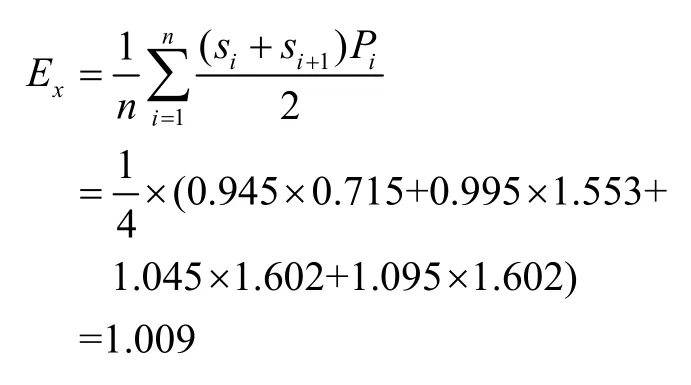
計算改進型灰色馬爾可夫預測值，預測結果如表8所示。

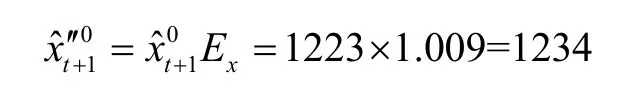
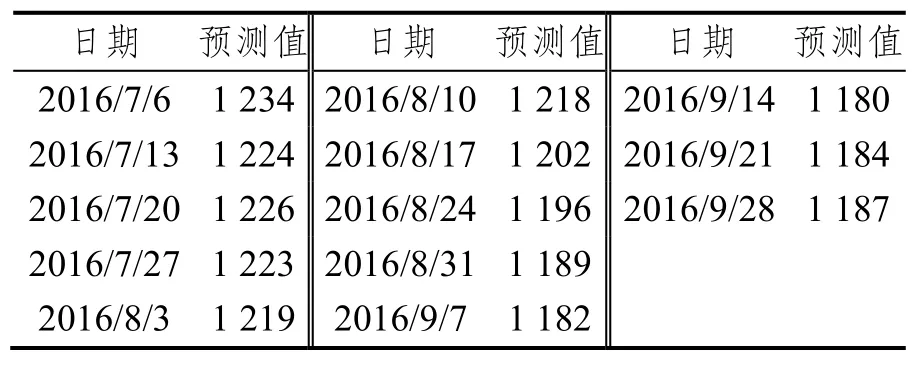
表8 改進型灰色馬爾可夫預測值Tab.8 The improved Gray-Markov predictions

3.4 預測精度判定

將2016年7月6日至2016年9月28日期間13周的公路運輸周價格預測值與實際值進行比對，計算出相對誤差q（x）分布如表9所示。

按照精度檢驗對照表進行預測精度的評定：在灰色模型的預測結果中，有2個預測精度達到Ⅰ級，9個為Ⅱ級，1個Ⅲ級，平均相對誤差2.48%；在灰色馬爾可夫模型的預測結果中，同樣有2個預測精度達到Ⅰ級，9個為Ⅱ級，1個Ⅲ級，平均相對誤差2.58%；而在改進型灰色馬爾可夫模型的預測結果中，則有3個預測精度達到Ⅰ級，8個為Ⅱ級，1個Ⅲ級，平均相對誤差2.11%。

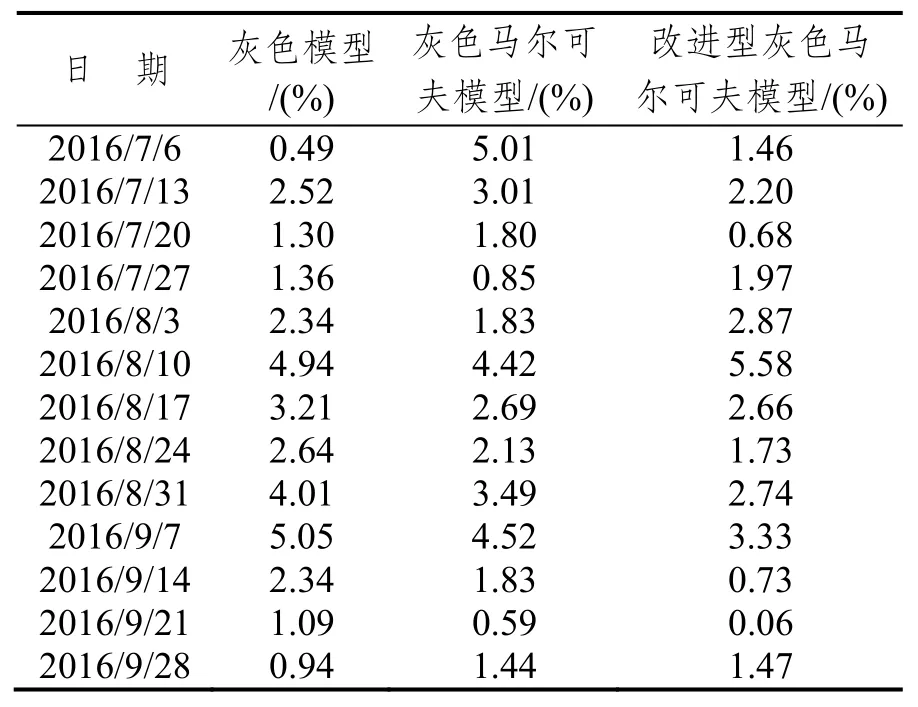
表9 相對誤差q（x）分布表Tab.9 Distribution of the relative error q(x)

最后，將灰色馬爾可夫模型的狀態區間以及預測曲線走勢繪制在圖1中。

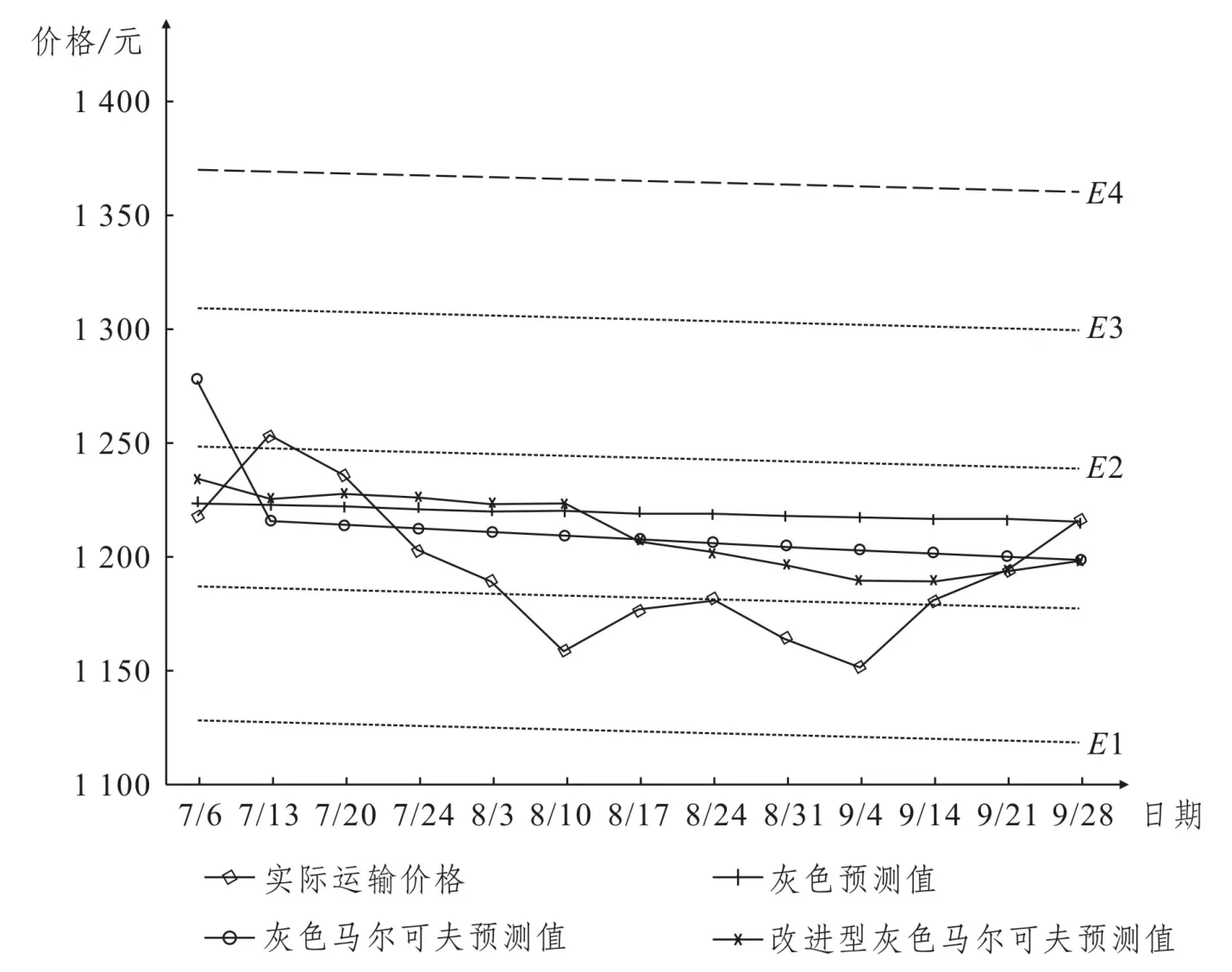
圖1 預測曲線對比圖Fig.1 Comparison of the predicted results

4 結 論

本文在灰色馬爾可夫模型中引入狀態轉移期望的概念，新構建出改進型灰色馬爾可夫預測模型。在對2016年7月6日至2016年9月28日的成都至南昌公路運輸周價格的預測結果中，改進型灰色馬爾可夫模型預測結果的精度等級更高，預測相對誤差更低，說明改進后的灰色馬爾可夫模型預測精度獲得了明顯提升。另外，在預測曲線對比圖1中，可以看出預測周期內的公路貨運實際價格大多處于E1、E2低狀態區間，說明2016年7月6日至2016年9月28日期間的公路貨運價格一直處于低位，而改進后的灰色馬爾可夫模型預測曲線對價格的這種下降趨勢反映的更明顯，更符合公路貨運價格隨市場波動變化的實際。

[1] 周榮康，徐永，李若靈. 基于灰色殘差GM（1，1）模型的道路交通量預測的研究[J]. 交通運輸工程與信息學報，2008，6（3）：49-53.

[2] 湯銀英，李龍. 基于Holt-Winters模型的鐵路月度貨運量預測研究[J]. 交通運輸工程與信息學報，2017，15（2）：1-5，13.

[3] 沈家軍，王煒，陳峻. 基于灰色馬爾可夫模型的近期公交客流量預測[J]. 公路交通科技，2007，9：120-123.

[4] 顧敬巖，吳群琪. 我國公路貨運市場價格的演進趨勢、問題及對策[J]. 交通運輸系統工程與信息，2013，6：191-197.

[5] 林巖，陳帥，陳燕，等. 道路交通事故的灰色馬爾科夫預測模型與算法[J]. 武漢理工大學學報：交通科學與工程版，2013，37（5）：924-928.

[6] 劉宗明，賈志絢，李興莉. 基于灰色馬爾科夫鏈模型的交通量預測[J]. 華東交通大學學報，2012，29（1）：30-34.

[7] 周盛世，楊麗紅，黃永強. 融合灰色理論與馬爾科夫鏈的青島市物流需求量預測[J]. 企業經濟，2011，30（10）：117-120.

[8] 崔勇，王川，陳小龍，等. 基于灰色馬爾科夫預測模型的中長期電力負荷預測[J]. 現代電力，2011，28（3）：38-41.

[9] 高陽，譚陽波.基于新維無偏灰色馬爾科夫預測模型的中長期能源消費預測[J].統計與決策，2007（22）：55-57.