基于隱含信任關系的概率張量分解推薦算法

趙超， 韓立新， 楊憶,2， 何戀

(1.河海大學,計算機與信息學院，南京 211100;2.淮北師范大學,計算機學院，安慶 235000)

0 引言

隨著互聯網的不斷發展，網絡中產生的信息呈爆炸性增長，出現了信息過載的現象，在此背景下，基于信息過濾技術的推薦系統應運而生。推薦系統試圖給用戶推送用戶可能感興趣的物品(包括音樂、電影、圖書等)。盡管傳統的基于協同過濾的推薦方法[1]已經被廣泛運用到像亞馬遜這種大型著名公司的商業系統中，但是仍存在數據稀疏性以及預測準確性的問題。

為了緩解上述兩個問題，很多學者對其進行了研究，并提出了很多有效的算法。Ma等人[2-3]通過在矩陣分解中加入社會正則化項、考慮利用用戶之間的直接信任關系進行推薦，這種方法忽視了用戶之間的隱含信任關系。Liu等人[4]基于上下文利用決策樹對數據進行分組，并融入社會關系進行推薦；Chen等人[5]考慮到存在離散的和連續的上下文，利用譜聚類對數據進行分組，并融入信任關系來提升推薦效果。這些方法只是利用上下文對數據進行預處理，并沒有將上下文融入到模型中。為了進一步提高推薦系統性能，本文通過鏈路預測的方法找出用戶之間的隱含信任關系并對利用上下文構建的張量進行分解[7-11]，提出基于隱含信任關系的概率張量分解推薦算法。

1 相關工作

1.1 用戶信任關系

1.2 概率矩陣分解

概率矩陣分解[6](PMF)是在基本的矩陣分解基礎上引入概率模型來進一步優化。PMF基于以下假設：觀測評分矩陣R以及近似矩陣R′服從高斯分布；用戶特征矩陣U以及物品特征矩陣V服從高斯分布。通過觀測評分矩陣已知值得到用戶特征矩陣U以及物品特征矩陣V，然后利用特征矩陣去預測觀測評分矩陣中的未知值。

假設有m個用戶對n個物品的評分矩陣，Rij表示用戶i對物品j的評分，根據貝葉斯推理，通過最小化如下目標函數來求解用戶特征矩陣U以及物品特征矩陣V：

1.3 網絡鏈路預測

網絡中的鏈路預測[13]是指如何通過已知的網絡節點以及網絡結構等信息預測網絡中尚未產生連邊的兩個節點之間產生連接的可能性，預測過程實際上是一種數據挖掘的過程。考慮到計算復雜度以及預測效果等因素，基于網絡結構相似性的方法被廣泛運用到鏈路預測中，因此本文采用基于局部信息的相似性指標進行預測(包括共同鄰居指數，Jaccard指數，Salton指數)，文獻[13]給出了多種相似性指標。考慮到社會信任關系網絡是有向圖，節點相似度計算公式如下:

共同鄰居指數：

Jaccard指數：

Salton指數：

其中，x和y表示社會信任網絡中任意兩個節點，Γout(x)和Γin(x)分別表示從節點x指向鄰居節點和從鄰居節點指向節點x的節點集合，kout(x)和kin(x)分別表示節點x的出度和入度，k為歸一化因子。

1.4 張量CP分解

(1)

1.5 協同主題回歸模型

協同主題回歸(CTR)模型是由Wang等人[14]提出的一種基于概率主題模型的協同過濾方法。Purushotham等人[15]將CTR模型與社會關系相結合來提升推薦效果。CTR模型將傳統的協同過濾方法與主題模型相結合，假設LDA模型生成K個主題，CTR的生成過程如下所示：

(1)對于每個用戶i，其潛在特征向量

(2)對于每個物品j：

a.主題后驗參數θj～Dirichlet(α)；

c.對于每個單詞，生成的主題zjn～Mult(θ)，單詞wjn～Mult(βzjn)；

2 基于隱含信任關系的概率張量分解推薦算法

2.1 概率張量分解

概率張量分解(PTF)可以看作是對PMF的一個推廣。由1.4節可知，一個N階張量χ可以通過CP分解得到N個因子矩陣U(1),…,U(N)。類似PMF，假設N個因子矩陣服從高斯分布，張量χ和近似張量χ′服從高斯分布。根據貝葉斯推理，通過最小化如下目標函數來求解因子矩陣U(i),如式(2)。

(2)

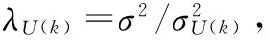
2.2 用戶隱含信任關系

現有的推薦算法只考慮了用戶之間的直接信任關系對推薦性能的影響，而忽視了用戶之間的隱含信任關系，本節給出尋找用戶隱含信任關系算法的偽代碼：

算法1:用戶隱含信任關系預測輸入:有向社會信任網絡圖對應的信任矩陣M,用戶數量U,選擇概率P輸出:用戶隱含信任關系矩陣N對于每個用戶u: 找出用戶的間接朋友節點(即用戶沒有直接指向的節點) 對于每個用戶u: 對于用戶u的每個間接朋友v: 利用1.3節中的相似度公式計算用戶u與其間接朋友的相似度S 如果S>P,則將Nuv置為S;否則將Nuv置為0 返回N

得到用戶隱含信任關系后，用戶潛在特征矩陣U(i)包含3個部分：用戶正則化項、用戶直接信任關系、用戶隱含信任關系。

2.3 提出的算法模型

由于考慮了用戶之間的隱含信任關系，CTR中的用戶潛在特征向量Ui～p(U)，如式(3)。

(3)

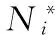
根據1.5節描述的CTR模型可知，物品潛在特征向量Vj是由物品內容和物品偏置共同構成的，可表示為式(4)。

(4)

根據2.1節可知通過概率張量分解得到的因子矩陣服從高斯分布且該張量也服從高斯分布，因此上下文特征向量可表示為式(5)。

(5)

如圖1所示。

圖1 融入隱含信任關系的PTF推薦算法模型

根據貝葉斯推理，我們提出的算法模型的后驗分布為式(6)。

(6)

2.4 參數學習

為了求上式的后驗概率最大值，通過對式(6)求對數，可以得到式(7)。

(7)

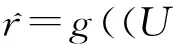
λf*∑f∈Ni*Tif*(Ui-Uf*)

(8)

(9)

(10)

給定U，V和C(1)…C(m)，采用EM算法來估計參數θj。設q(zjn=k)=Φjnk，將上述目標函數中包含θj的項分離出來，利用Jensen不等式得到式(11)。

(11)

L(θj,Φj)是L(θj)的下界，將L(θj,Φj)不斷逼近L(θj)從而得到最優解，可以采用梯度投影法來優化θj。

得到U，V，C，θ，Φ后，可以通過下式來優化β為式(12)。

βkw∝∑j∑nΦjnk1[wjn=w]

(12)

2.5 相關工作比較

矩陣分解技術已經成功運用于各類推薦算法中。通過對用戶的評分矩陣進行分解來預測未評分物品的分數，根據分數的高低生成最終的推薦結果。文獻[6]從概率的角度對用戶的評分矩陣進行分解，提出PMF模型，該方法對于稀疏數據集有很好的性能，但是PMF方法沒有充分利用用戶之間的信任關系，因此文獻[3]給出一種基于用戶信任關系的推薦算法，在矩陣分解過程中加入用戶信任關系進行推薦。雖然該方法在一定程度上可以提高推薦效率，但是并沒有考慮上下文對用戶評分的影響；文獻[4-5]提出一種上下文感知的推薦算法，首先利用上下文運用分類或聚類算法對數據進行分塊，再對每個分塊的數據進行矩陣分解，這種方法雖然加入了上下文對評分的影響，但是并沒有讓上下文參與分解過程，并不能體現上下文在推薦上的優勢。因此本文在矩陣分解的基礎上進行推廣，結合上下文將用戶評分數據用張量表示，并在張量分解的過程中利用用戶之間的直接信任關系以及隱含信任關系來提升推薦效果。

3 實驗結果及分析

3.1 數據集

本文實驗使用的數據集為Epinions數據集，我們從Epinions數據集中挑選2 784名用戶對25 626個商品的評分數據，其中包括47 434條評分記錄以及33 282條直接信任關系，利用2.2節中的算法1預測出346 567條隱含信任關系，并選取物品評分的平均值作為上下文構建張量參與計算。通過隨機采樣的方法進行實驗。

3.2 實驗結果與分析

采用文獻[4]提出的SoCo算法和文獻[5]提出的C-CTR-SMF2算法與本文提出的基于隱含信任關系的概率張量分解推薦算法(ITR-PTF)進行比較,采用MAE、RMSE來衡量預測誤差，采用F1值來衡量推薦質量。

實驗中，選取主題數量K=100，潛在特征矩陣維度D=30。SoCo算法中設置參數λ=0.1，α=0.01時能夠達到最好性能；C-CTR-SMF2算法設置參數D=30，λU=0.01,λf=0.01，λV=1時能達到最好性能；本文提出的ITR-TF算法設置參數D=30，λU=λf=λf*=0.01，λC=λV=1。不同算法的MAE和RMSE對比結果，如表1所示。

表1 不同算法性能對比

不同算法進行topN推薦時F1值變化,如圖2所示。

圖2 不同算法F1值對比

圖2表明推薦3-5個物品時推薦性能較好。從表1中可以看出C-CTR-SMF2算法的MAE、RMSE值小于SoCo算法，F1@5值大于SoCo算法，表明C-CTR-SMF2算法推薦效果優于SoCo算法，這是因為C-CTR-SMF2算法不僅結合了上下文信息以及信任關系，還利用CTR模型對物品內容進行建模。本文提出的ITR-PTF算法推薦效果優于C-CTR-SMF2算法，因為相比C-CTR-SMF2算法，ITR-PTF算法將上下文信息融入到構建的模型中，利用上下文構建張量并將用戶的隱含信任關系加入到張量分解過程中，充分利用上下文以及用戶信任關系來提高推薦的性能。

4 總結

本文提出了一種基于隱含信任關系的概率張量分解推薦算法，首先利用上下文構建用戶在上下文中的評分張量，同時根據LDA模型結合物品內容對物品進行解釋，其次考慮了用戶直接信任關系的同時還考慮了用戶的隱含信任關系對推薦性能的影響，最終在傳統的推薦方法中加入上下文、用戶信任關系、物品內容構建推薦模型。實驗結果表明，本文所提出的算法可以從一定程度上緩解數據的稀疏性問題，并且具有更高的準確率。

[1] Adomavicius G, and Tuzhilin A. Toward the next Generation of Recommender Systems: A Survey of the State-of-the-Art and Possible Extensions[J]. IEEE Transactions on Knowledge & Data Engineering, 2005, 17(6): 734-749.

[2] Ma H, Zhou D Y, et al. Recommender Systems with Social Regularization[C]//Forth International Conference on Web Search & Web Data Mining. Hong Kong, 2011: 287-296.

[3] Ma H, King I, Lyu M R. Learning to recommend with social trust ensemble[C]//International ACM SIGIR Conference on Research and Development in Information Retrieval. Boston, 2009: 2003-210.

[4] Liu X, Aberer K. SoCo: A Social Network Aided Context-Aware Recommender System[C]//International Conference on World Wide Web. Rio de Janeiro, 2013: 781-802.

[5] Chen C, Zheng X, Wang Y, et al. Context-Aware Collaborative Topic Regression with Social Ma- trix Factorization for Recommender Systems[J]. Palo Alto California Aaai Press, 2014, 3(3): 239-242.

[6] Salakhutdinov R, Mnih A. Probabilistic matrix factorization[C]//International Conference on Machine Learning, Edinburgh, 2012: 880-887.

[7] Matrix and Tensor Factorization Techniques for Recommender System[M]. Springer Internatio- nal Publishing,2016.

[8] Luan W J, and Jiang C J.Collaborative Tensor Factorizaiton and its Application in POI recommendation[C]//IEEE 13th International Conference on Network, Sensing, and Control, Mexico City, 2016.

[9] Tan H C, Feng G D, et al. A tensor-based method for missing traffic data completion[J]. Transp- ortation Research (Part C), 2013, 28: 15-27.

[10] Zhao S, Lyu M R, King I. Aggregated Temporal Tens-or Factorization Model for Point-of-intrest Recommendation [M]. Neural Information processing. America: Springer International Publishing, 2016.

[11] Frolov E, Oseledets I. Tensor Methods and Recommender Systems[J]. Computer Science, Cornell University Library, arXiv: 1603.06038, 19 Mar 2016.

[12] Kolda T G, Bader B W. Tensor Decompositions and Applications[J]. Siam Review, 2009, 51(3): 455-500.

[13] Martinez V, Berzal F, et al. A Survey of Link Prediction in Complex Networks[J]. ACM Computing Surveys, University of Granada, 2016, 49(4):1-33.

[14] Wang C, Blei D M. Collaborative topic modeling for recommending scientific articles[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego, 2011: 448-456.

[15] Purushotham S, Liu Y, Kuo C C J. Collaborative Topic Regression with Social Matrix Factorization for Recommendation Systems[C]//Proceedings of the 29th International Conference on Machine Learning. Edinburgh, UK, 2012.