基于預估-反饋聯(lián)合處理的射頻噪聲干擾抑制算法

王國宏，孫殿星，白杰，張翔宇

海軍航空大學, 信息融合研究所,煙臺 264001

現(xiàn)代雷達所面臨的電磁環(huán)境日益惡劣，針對雷達的電磁干擾技術(shù)迅速發(fā)展，噪聲壓制干擾作為一種常用的干擾類型，通過在時域和頻域?qū)δ繕嘶夭ㄐ盘栃纬扇采w達到其壓制干擾效果，其中射頻噪聲干擾相比于噪聲調(diào)制類干擾，其信號熵值最大且遮蓋性較好[1]，從而增大了雷達對抗的難度，同時，線性調(diào)頻(Linear Frequency Modulation, LFM)信號具有較大的時寬帶寬積，能夠同時滿足作用距離和距離分辨率的要求，從而被廣泛應用于現(xiàn)代雷達系統(tǒng)中,所以適用于脈沖壓縮雷達的射頻噪聲干擾抑制技術(shù)對雷達的實戰(zhàn)和發(fā)展具有實際性的推動作用。

目前，國內(nèi)外學者在噪聲干擾抑制方面做了大量研究，文獻[2-3]通過不同算法實現(xiàn)目標回波信號與干擾信號的分離，從而達到干擾抑制的目的；文獻[4-6]分別提出了在干擾背景下直接進行目標檢測的算法；文獻[7-8] 利用LFM信號在分數(shù)階傅里葉變換(FRFT)域的處理增益，通過構(gòu)建濾波器實現(xiàn)干擾抑制。上述文獻基于信號層的處理，從不同角度入手，較好的實現(xiàn)了對噪聲壓制干擾的抑制，但是上述文獻均未建立合理的干擾抑制檢驗量，而算法參數(shù)又很難在沒有任何先驗信息的情況下達到最優(yōu)，從而導致算法實時性以及在不同環(huán)境下的“應變能力”較差。

文獻[9]通過點跡關(guān)聯(lián)、數(shù)據(jù)壓縮以及數(shù)據(jù)跟蹤等技術(shù)，解決了壓制干擾下雷達目標檢測概率低的問題；文獻[10] 通過建立量測模型及序貫濾波跟蹤，提升了組網(wǎng)雷達的目標檢測與跟蹤能力；文獻[11] 提出了點目標概率多假設跟蹤(DC-PPMHT)算法，降低了航跡丟失率；文獻[12] 依據(jù)干擾強度選擇基于粒子濾波的檢測前跟蹤(PF-TBD)或門限自適應的多假設跟蹤，提高了遠距離支援干擾下的目標跟蹤能力。上述文獻利用目標點跡和噪聲點跡的不同特征，通過數(shù)據(jù)層處理達到了干擾抑制的目的，但由于缺乏目標運動的先驗信息，為減小漏檢概率，會在較大的速度、加速度以及運動方向范圍內(nèi)對目標點跡進行檢測，從而導致當壓制干擾較強，噪聲點跡較密集時，過多的噪聲點跡滿足判決條件，造成真實目標的檢測以及跟蹤困難。

針對上述文獻所出現(xiàn)的問題，本文提出了一種基于預估-反饋聯(lián)合處理的射頻噪聲干擾抑制技術(shù)，通過將信號層的信號估計算法和數(shù)據(jù)層的航跡檢測算法相結(jié)合，并對反饋調(diào)節(jié)環(huán)節(jié)進行構(gòu)建，有效實現(xiàn)了射頻噪聲干擾的抑制。

1 問題描述

假設在一段觀測時間內(nèi)目標的運動速度不變，在強射頻噪聲干擾環(huán)境下脈壓警戒雷達所接收到的回波信號x(t)為

JRF(t)+n(t)

(1)

式中：si(t)為第i個目標的回波信號；Ai、fi和φi(i=0,1,…,k-1)分別為第i個目標回波的幅度、載頻和相位；μ為LFM信號的調(diào)制斜率；n(t)為背景噪聲，包括接收機熱噪聲、電磁環(huán)境噪聲、雜波噪聲等，為高斯白噪聲；JRF(t)為射頻噪聲干擾，由帶限高斯白噪聲放大產(chǎn)生，其時域表達式為

JRF(t)=Uj(t)cos[ωjt+φ(t)]

(2)

式中：Uj(t)為包絡函數(shù)，服從瑞利分布；φ(t)為相位函數(shù)；ωj為中頻窄帶噪聲的中心頻率，且ωj遠大于JRF(t)的譜寬。

由式(1)可以看出，強射頻噪聲干擾環(huán)境下的干擾抑制技術(shù)需要解決以下幾個問題：

1)射頻噪聲干擾在時域和頻域?qū)FM信號形成全覆蓋，如何在強噪聲干擾環(huán)境下利用信號特性差異實現(xiàn)干擾能量消除，是信號層處理需要解決的難題。

2)信號層處理之后，噪聲點跡與目標點跡并存，如何對所有可能形成的航跡進行檢測以減小漏檢概率，是數(shù)據(jù)層處理需要解決的難題。

3)信號層的干擾消除效果依賴于算法參數(shù)的選擇，如何利用數(shù)據(jù)層對航跡的實時估計，對信號層算法參數(shù)進行調(diào)整，是聯(lián)合處理需要解決的難題。

2 射頻噪聲干擾抑制技術(shù)

綜合考慮以上問題，本文擬從以下3個方面進行強射頻噪聲干擾的抑制：①信號層窄帶濾波，以解決干擾消除問題；②數(shù)據(jù)層邏輯判決，以解決航跡生成問題；③反饋調(diào)節(jié)，以解決參數(shù)調(diào)節(jié)問題。本文總體思路如圖1所示。

2.1 基于信號估計的窄帶濾波干擾消除

首先對回波信號進行盲源分離預處理，以解決目標回波之間的交叉干擾[13]問題，然后利用LFM信號在FRFT域不同階次的不同特性，通過對LFM信號能量聚集點的坐標估計，構(gòu)建窄帶濾波器進行信號層干擾消除。基于坐標估計的信號層窄帶濾波干擾消除原理如圖2所示。

圖中：B為LFM信號帶寬；T為LFM信號時長。在FRFT某一變換階次，如圖2中軸所示，LFM信號表示為復正弦信號，且正弦信號載頻與LFM信號的載頻存在確定關(guān)系，因此利用子空間正交方法[14]可以完成LFM信號的檢測和參數(shù)估計，而在FRFT域的正交變換階次，如圖2中軸所示，LFM信號表現(xiàn)為沖激函數(shù)，此時能夠根據(jù)參數(shù)估計結(jié)果對LFM信號的能量聚集點坐標進行估計，并基此構(gòu)建窄帶濾波器，完成濾波處理。

2.1.1 Fast ICA算法盲源分離預處理

由式(1)可以看出，在實際干擾環(huán)境下，雷達所接收的信號是由不同目標回波和干擾信號組成的混合信號，由于不同目標回波信號之間相互獨立，且滿足非高斯分布的要求，所以本文首先采用獨立成分分析(ICA)算法對多分量LFM信號進行分離，同時考慮到基于最大負熵理論的Fast ICA算法收斂速度為3階，較ICA算法的線性收斂速度更快，算法實時性更強，所以本文最終采用Fast ICA算法對回波信號進行處理。

假設戰(zhàn)場環(huán)境中目標個數(shù)n不大于接收系統(tǒng)的通道數(shù)m，采用多通道寬帶接收體制對多分量LFM信號進行接收，復數(shù)信號矩陣形式表示為

X=AS

(3)

式中：X=[x1x2…xm]T為m個觀測復數(shù)信號矢量；S=[s1s2…sn]T為n個獨立復數(shù)信號矢量包括n-1路LFM信號和1路噪聲干擾信號；A=[ωij]為m×n維復數(shù)混合矩陣，并且A列滿秩。Fast ICA算法主要包括中心化、白化和獨立分量提取3個步驟，其處理流程如圖3所示。

(4)

(5)

最后提取獨立分量，采用峭度來衡量分離信號的非高斯性，由于目標回波信號滿足非高斯分布，所以如果存在矩陣B，使得Y=BHZ的各個分量的峭度值離零值最遠，則認為Y是對源信號S的估計。對于矩陣B的具體求解過程可參考文獻[15]，本文在此不再贅述。

通過對回波信號進行Fast ICA預處理，使得不同分量目標回波信號相分離，既減小了強目標回波信號對弱目標回波信號檢測的影響，同時對信號信干比也有所改善。

2.1.2 LFM信號檢測與參數(shù)估計

在強噪聲干擾環(huán)境下，目標回波(LFM)信號在FRFT域的能量聚集點被干擾信號所淹沒，從而導致傳統(tǒng)的基于峰值搜索的聚集點坐標估計算法不再適用，但是濾波器始末位置的確定需要以LFM信號的能量聚集點坐標為參考，為此，本文利用子空間正交方法更優(yōu)的抗干擾能力，首先進行LFM信號的檢測和參數(shù)估計[16-17]，然后再根據(jù)參數(shù)估計結(jié)果進行聚集點坐標的估計。

經(jīng)過Fast ICA預處理后，除噪聲分量之外各分量信號統(tǒng)一表示為

r(t)=s(t)+N(t)=exp{-j[(ω0+ωd)t+

μt2/2+φ]}+N(t)

(6)

式中：ω0為發(fā)射信號載頻；ωd為目標多普勒頻移；N(t)為噪聲干擾信號，滿足高斯分布。

當FRFT變換角度α1滿足α1=-arctanμ時，LFM信號的FRFT變換為[18]

Aexp(-juωcosα1)

(7)

式中：w為LFM信號的載頻；

exp[-j(ω2sinα1cosα1-φ)/2]。

由式(7)可以看出Sp(u)為一個嚴格的復正弦信號，定義此時的變換階次為LFM信號的平行變換階次。由于FRFT是線性變換，式(6)的FRFT變換為

Rp(u)=A′exp(-jωnu)+Np(u)

(8)

式中：ωn=(ω0+ωd)cosα1為正弦信號角頻率；A′為復值常量；Np(u)=FRFTp[N(t)]，滿足高斯分布。

對式(8)進行抽樣，并用矩陣形式表示：

R(k)=A′exp(jkωn)γ+N(k)

(9)

式中：γ=[1ejωn…ejmωn]T；N(k)=[Np(k)Np(k+1)…Np(k+m)]T。

向量R(k)的協(xié)方差矩陣為

(10)

由于矩陣rank(γγH)=1，根據(jù)文獻[19]的結(jié)論容易證明：

(11)

由于多普勒頻移的存在，當分量信號中存在目標回波信號時，信號頻率滿足：

(12)

式中：wdmax為多普勒頻移最大值。

通過子空間正交方法最終得到LFM信號的載頻為

(13)

以上完成了LFM信號的檢測和估計，當有LFM信號存在時，根據(jù)以上所得到的載頻估計，可以對LFM信號在FRFT域的能量聚集點坐標進行估計，進而構(gòu)建窄帶濾波器，完成窄帶濾波過程。

2.1.3 LFM信號窄帶濾波

由于LFM信號的線性時頻特性使得LFM信號在FRFT域具備能量高度聚集的特征，而射頻噪聲干擾以及過程噪聲則不具備此特征，據(jù)此建立窄帶濾波器，使得LFM信號的能量包含在濾波器寬度范圍之內(nèi)，而干擾以及噪聲的能量在濾波器寬度范圍之外，以此在完整保留LFM信號能量的前提下濾除大部分干擾和噪聲的能量[20]。

當變換角度α2與LFM信號的調(diào)頻率正交時，即α2=arctan(-1/2πμ)，LFM信號的FRFT變換可表示為

|Sp(u)|=|A(t)Aα2σ(ω-ucosα2)|

(14)

由式(14)可以看出，當變換角度α2與LFM信號的調(diào)頻率正交時，LFM信號在u域表現(xiàn)為沖激函數(shù)，具有明顯的能量聚集效果，并稱此時的變換階次為FRFT域LFM信號的正交變換階次。根據(jù)LFM信號的能量聚集特性構(gòu)建窄帶濾波器，使濾波器輸出在完整保留LFM信號能量的同時，濾除大部分噪聲干擾能量。

為了對量綱進行歸一化處理，引入尺度因子S=T/fs，定義新的尺度化坐標為

(15)

式中：T為觀測時間；fs為采樣頻率。新的坐標實現(xiàn)了無量綱化。

根據(jù)式(13)，LFM信號在(p,u)二維平面上的能量聚集點坐標(p0,u0)估計為

(16)

L=2ρsin(p0π/2)S/(2πcosα1)+2/B

(17)

式中：ρ為目標多普勒頻率的估計誤差標準差。由式(17)可以看出，載頻的估計精度直接決定著濾波器寬度L的取值。

2.2 基于邏輯判決的數(shù)據(jù)層航跡檢測

在恒虛警檢測形成點跡之后，利用目標的運動特性在數(shù)據(jù)層對點跡進行處理：由于受機動性能的影響，目標點跡滿足一定的分布規(guī)律，而噪聲點跡則呈現(xiàn)出無序性的特點，運用M/N邏輯法對所有可能生成的航跡進行檢測，并根據(jù)信號層對目標運動狀態(tài)的估計，利用徑向速度方向判決算法，對不滿足要求的噪聲航跡進行剔除。

2.2.1 基于M/N邏輯法的航跡檢測

M/N邏輯法是以多重假設的方式通過預測和相關(guān)波門來確認可能存在的航跡，當N個掃描周期中有M個觀測點落入相關(guān)波門中時判斷航跡起始成功。

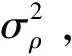
(18)

式中:c為光速。

量測協(xié)方差矩陣R為[22]

(19)

式中：

(20)

運用M/N邏輯法對目標進行檢測。其具體工作方式如圖4所示。

1)在xoy坐標系中，以暫時航跡的第一個點p1[x(1) y(1)]為圓心，以vmaxt、vmint為半徑構(gòu)建圓環(huán)形關(guān)聯(lián)區(qū)域。如果在下一個掃描周期雷達在此區(qū)域內(nèi)觀測到新的點跡，則暫時航跡形成第2個點p2[x(2) y(2)]， 否則刪除該暫時航跡。vmax、vmin分別

為目標運動的最大速度和最小速度,t為雷達的掃描周期。

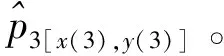
(21)

式中：

(22)

這里D3是服從自由度為m的χ2分布的隨機變量。由給定的門限概率查表可得門限γ，若第3次掃描量測所得的最小D3min值小于γ，則對該D3min值所對應的量測點p3[x(3) y(3)]給予互聯(lián)。此后重復步驟2)，從而完成目標檢測。

通過M/N邏輯法可以實現(xiàn)對目標的檢測，但是由于噪聲點跡較密集的原因，可能存在檢測到的航跡為噪聲航跡的情況，所以需要對所有檢測到的航跡進行進一步的判決。

2.2.2 基于徑向速度方向判決的噪聲航跡剔除

通過信號層處理可以對目標的多普勒頻率進行估計，而在M/N邏輯法中并沒有對目標的徑向速度加以約束，所以可以將一部分徑向速度不滿足多普勒頻率估計的航跡進行剔除，實現(xiàn)目標航跡的預估檢測。

設k1、k2時刻的點跡坐標分別為(x1,y1)和(x2,y2)，則數(shù)據(jù)層對k2時刻目標的多普勒頻率估計為

(23)

式中：sign(·)為取符號函數(shù)；λ為雷達工作波長。

由式(13)可以得到信號層對目標當前時刻的多普勒頻率估計為

(24)

由于信號層對目標徑向速度的估計精度較低，所以在此只根據(jù)所估計的多普勒頻率方向進行判決。對每個時刻的航跡點進行如下判決：

對于某一條航跡而言，當速度估計矛盾的時刻數(shù)大于d時，判定航跡為噪聲航跡，并予以剔除。

通過徑向速度方向判決，一部分不滿足判決要求的航跡被剔除，但同時需要注意的是，通過徑向速度方向判決的方法并不能從根源上解決噪聲航跡的產(chǎn)生問題。噪聲航跡的產(chǎn)生來源于噪聲點跡，只有通過調(diào)整濾波器的濾波中心以及帶寬，才能減少噪聲點跡的數(shù)量，從而降低噪聲航跡產(chǎn)生的概率，所以，接下來對窄帶濾波器的反饋調(diào)節(jié)環(huán)節(jié)進行構(gòu)建。

2.3 基于反饋調(diào)節(jié)的聯(lián)合處理

2.3.1 反饋調(diào)節(jié)的原因

由式(17)的分析可知，目標多普勒頻率的估計精度直接影響著濾波器寬度的取值，進而影響到濾波效果的好壞，但是受采樣頻率等因素的影響，信號層對目標多普勒頻率的估計精度較低，從而導致濾波效果較差，增大了數(shù)據(jù)層噪聲航跡產(chǎn)生的可能性。

但同時，隨著觀測時間的延長，數(shù)據(jù)層能夠得到較為準確的航跡徑向速度估計，并且在一定時長后，能夠?qū)⒐烙嬚`差保持在較低的水平。因此，可以利用數(shù)據(jù)層對航跡徑向速度估計的反饋對窄帶濾波器的參數(shù)進行實時調(diào)整，從而使濾波效果更好，從根本上解決噪聲航跡的產(chǎn)生問題。

2.3.2 基于數(shù)據(jù)層反饋信息的濾波器調(diào)節(jié)

設k時刻對目標的速度預測矢量V為

(25)

(26)

則V在τ方向上的投影為

(27)

投影的方差為

(28)

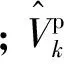
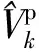
第k時刻濾波器中心坐標修正為

(29)

根據(jù)正態(tài)分布的“3σ”原則，將濾波器寬度修正為

(30)

通過式(29)和式(30)實現(xiàn)了利用數(shù)據(jù)層的反饋信息對濾波器參數(shù)進行實時調(diào)整。對于目標航跡而言，通過反饋可以使濾波器達到更好的濾波效果，從而減少噪聲點跡對目標航跡的干擾；而對于噪聲航跡而言，噪聲點跡的減少會直接造成其航跡中斷。

2.4 總體思路流程圖

本文的射頻噪聲干擾抑制技術(shù)流程圖如圖5所示。

3 仿真實驗

為了驗證預估-反饋聯(lián)合處理算法的有效性，本文從信號層算法、數(shù)據(jù)層算法以及反饋調(diào)節(jié)算法3部分對射頻噪聲干擾的抑制問題進行仿真實驗，并與現(xiàn)有算法進行比較。

3.1 仿真條件設置

設雷達發(fā)射的LFM信號脈寬為50 μs，帶寬為5 MHz，載頻為5 GHz，中頻為1 MHz，中頻采樣頻率為15 MHz；雷達掃描周期為5 s，測距和測角誤差分別為100 m和0.2°。射頻噪聲干擾信號的帶寬為20 MHz，能夠在頻帶上覆蓋目標回波信號，目標參數(shù)信息如表1所示。

在雷達回波信號信干比為-25 dB條件下進行仿真實驗。

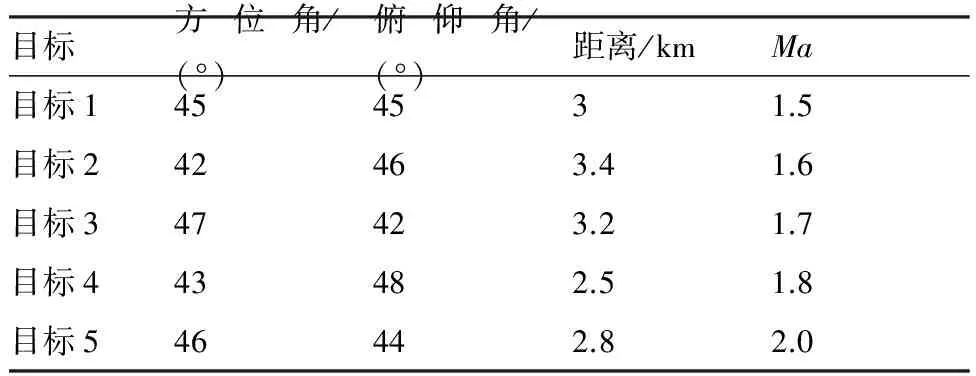
表1 目標參數(shù)Table 1 Target parameters

3.2 仿真結(jié)果與分析

3.2.1 信號層處理仿真驗證

1)首先為驗證本文信號層處理算法的有效性，與現(xiàn)有的基于峰值搜索的FRFT域濾波算法進行比較分析，其仿真結(jié)果如圖6和圖7所示。

圖6為信干比為-25 dB條件下，LFM信號在FRFT域正交階次的譜分布情況。由圖6可以看出，信干比為-25 dB時，LFM信號在FRFT域的能量聚集點被完全淹沒在噪聲干擾中，無法通過峰值搜索的方法得到能量聚集點坐標。

圖7為信干比為-25 dB條件下，通過子空間正交法得到的信號偽譜分布，其中，類似脈沖的尖峰代表復正弦信號所對應的角頻率。由圖7可以看出，信干比為-25 dB時，復正弦信號的角頻率能夠較準確的被估計出來，進而根據(jù)式(14)得到能量聚集點坐標。

表2所示為在不同信干比條件下，本文算法與峰值搜索算法的坐標估計均方根誤差對比。

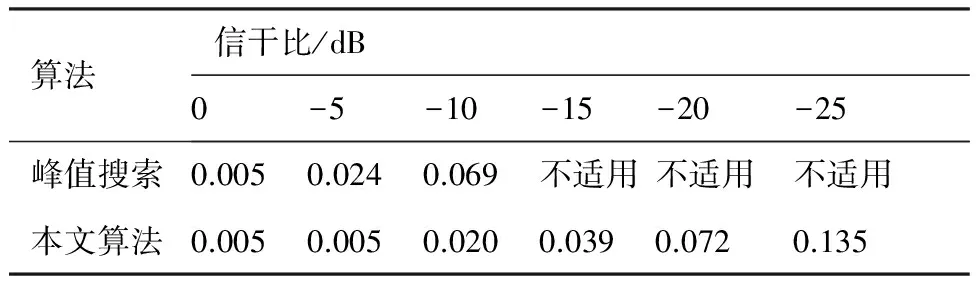
表2 與傳統(tǒng)算法均方根誤差(RMSE)對比

由表2數(shù)據(jù)可以看出，本文的坐標估計算法在估計精度以及穩(wěn)定性方面均優(yōu)于傳統(tǒng)的峰值搜索算法。

通過以上仿真實驗可以看出，相比于峰值搜索算法，本文所提算法抗噪聲干擾能力更強，能夠在信干比更低時實現(xiàn)LFM信號的檢測和參數(shù)估計。

2)為進一步驗證本文所提算法的有效性，對窄帶濾波算法進行仿真驗證，并給出了濾波前后的對比如圖8和圖9所示。圖8(a)和圖8(b)分別為窄帶濾波前后的脈沖壓縮結(jié)果，其中標注點表示目標所在位置。圖9(a)和圖9(b)分別為窄帶濾波前后連續(xù)5個掃描周期所得到的點跡情況。

通過圖8(a)和圖8(b)的對比可以看出，本文算法在較好保留目標回波信息前提下濾除了大部分干擾信號；通過圖9(a)和圖9(b)的對比可以看出，窄帶濾波之后所生成的點跡數(shù)量明顯減少，從而有利于數(shù)據(jù)層對目標的檢測。

結(jié)合本文算法，定義干擾抑制比為窄帶濾波前后信干比的差值，則干擾抑制比隨輸入信號信干比的變化情況如圖10所示。

圖10中橫坐標表示回波信號信干比，縱坐標表示干擾抑制比，隨著信干比的增大，干擾抑制比的增大趨勢逐漸減緩，并最終在信干比為35 dB時出現(xiàn)下降，其原因在于：回波信號信干比增大，使得LFM信號的載頻估計誤差增大，根據(jù)式(17)，濾波器的寬度逐漸增大，最終導致窄帶濾波的干擾濾除效果下降。

3.2.2 數(shù)據(jù)層處理仿真驗證

為驗證本文數(shù)據(jù)層處理算法的有效性，對目標檢測算法進行仿真驗證。應用M/N邏輯法對窄帶濾波之后連續(xù)5個掃描周期的點跡進行目標檢測，仿真結(jié)果如圖11所示。

圖11為對連續(xù)5個掃描周期的點跡進行目標檢測所形成的航跡情況。由圖11可以看出，M/N邏輯法能夠?qū)δ繕诉M行檢測，但同時，由于噪聲點跡較密集分布在目標周圍，所以一部分由噪聲點跡形成的噪聲航跡也被誤檢出來。

進一步對徑向速度方向判決算法進行仿真驗證，其仿真結(jié)果如圖12所示。圖12為根據(jù)徑向速度判決對圖10中的噪聲航跡進行剔除后的結(jié)果。由圖12可以看出，徑向速度判決能夠?qū)σ徊糠謴较蛩俣炔粷M足判決條件的噪聲航跡進行剔除，效果較為明顯。

徑向速度判決前后，噪聲航跡的平均生成數(shù)量如表3所示。由表3可以看出，經(jīng)過徑向速度方向判決，噪聲航跡的生成數(shù)量在很大程度上有所減少。同時仍有部分噪聲航跡被保留下來，所以需要進一步通過數(shù)據(jù)層的反饋調(diào)節(jié)對噪聲航跡進行剔除。

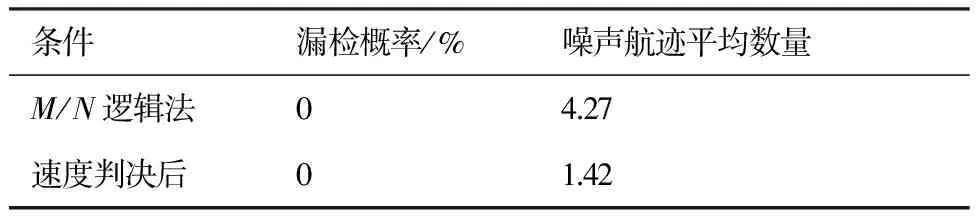
表3 噪聲航跡數(shù)量對比Table 3 Comparison of noise track numbers

3.2.3 反饋調(diào)節(jié)仿真驗證

為驗證反饋調(diào)節(jié)的有效性，對濾波器在不同時刻的參數(shù)進行記錄，其變化情況如表4所示。

表4為目標5的濾波中心以及濾波器帶寬的變化情況，其中，LFM信號的能量聚集點坐標為1.736 8。由表4可以看出，加入反饋調(diào)節(jié)之后，濾波器的中心更加接近于能量聚集點坐標，并最終保持在很小的誤差范圍內(nèi)，同時濾波器帶寬也逐漸變窄，從而對噪聲起到了較好的濾除效果。

為進一步驗證反饋調(diào)節(jié)的有效性，對加入反饋調(diào)節(jié)之后數(shù)據(jù)層的目標檢測情況進行仿真驗證，其目標檢測效果如圖13所示。

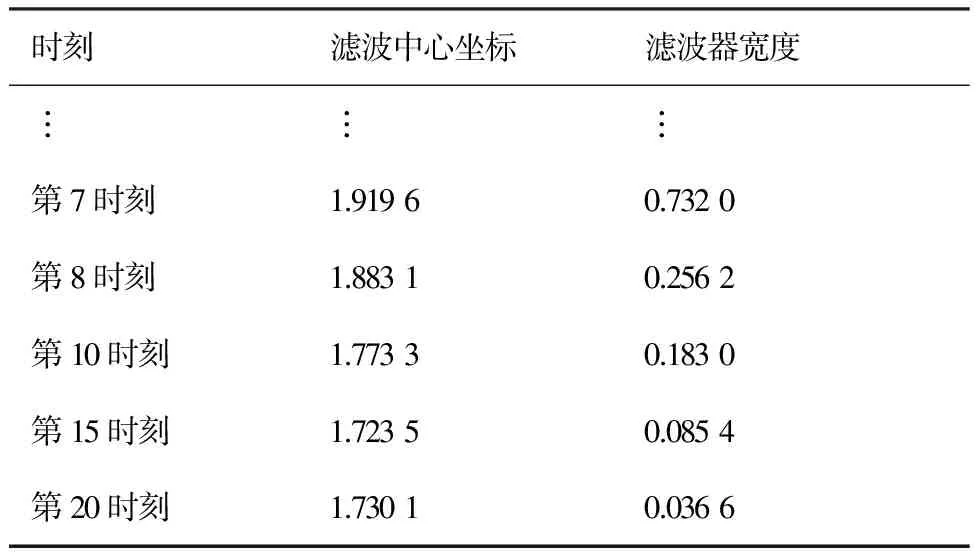
表4 濾波器參數(shù)Table 4 The filter parameter

圖13為加入反饋調(diào)節(jié)之后的目標檢測的結(jié)果。由圖13可以看出，數(shù)據(jù)層的反饋調(diào)節(jié)對目標航跡沒有產(chǎn)生影響，而對于噪聲航跡而言，數(shù)據(jù)層的反饋直接導致了其航跡中斷，可見，數(shù)據(jù)層的反饋調(diào)節(jié)能夠起到較好的噪聲航跡剔除作用。

將本文算法與文獻[24]中算法的目標檢測概率進行比較，蒙特卡羅實驗次數(shù)為200次，實驗結(jié)果如圖14所示。

由圖14可以看出，本文算法優(yōu)于文獻[24]中的算法，并且將壓制干擾下的目標檢測信干比提高了約10 dB左右，能夠應用于信干比更低時的情況。

4 結(jié) 論

針對射頻噪聲干擾抑制問題，本文提出了一種預估-反饋聯(lián)合處理算法。通過仿真實驗證明了本文算法能夠在信干比較低的情況下，實現(xiàn)對射頻噪聲干擾的抑制以及對目標的檢測，并且該算法較傳統(tǒng)算法具有更優(yōu)的干擾抑制能力。

1)通過對信號層算法與數(shù)據(jù)層算法關(guān)聯(lián)信息的提取以及反饋調(diào)節(jié)量的構(gòu)建，實現(xiàn)了對射頻噪聲干擾的一體化抑制，有效提高了本文算法的干擾抑制能力。

2)利用數(shù)據(jù)層對目標徑向速度的預測信息，合理構(gòu)建能夠調(diào)節(jié)信號層算法參數(shù)的反饋調(diào)節(jié)量，從而保證信號層處理算法的有效性和實時性。

3)通過仿真實驗與文獻[24]中基于Radon-分數(shù)階傅里葉變換的算法進行了比較，證明了本文算法在射頻噪聲干擾環(huán)境中具有更好的目標檢測能力。

參 考 文 獻

[1] 趙國慶. 雷達對抗原理[M]. 西安: 西安電子科技大學出版社, 2012: 122-123.

ZHAO G Q. Radar countermeasure principle[M]. Xi’an: Xidian University Press, 2012: 122-123 (in Chinese).

[2] 李冬霞, 崔顏敏, 劉海濤, 等. 基于JADE的測距儀脈沖干擾抑制技術(shù)[J].系統(tǒng)工程與電子技術(shù), 2016, 38(2): 423-427.

LI D X, CUI Y M, LIU H T, et al. Distance measure equipment impulse interference mitigation method based on JADE[J]. Systems Engineering and Electronics. 2016, 38(2): 423-427 (in Chinese).

[3] 溫媛媛, 陳豪. 基于時域卷積盲信號分離的雷達干擾抑制技術(shù)算法[J].中國科學院大學學報, 2013, 30(4): 523-527.

WEN Y Y, CHEN H. Algorithm of radar interference suppression based on blind signal separation in the time domain[J]. Journal of University of Chinese Academy of Sciences, 2013, 30(4): 523-527 (in Chinese).

[4] JONEIDI M, ZAEEMZADEH A, REZAEIFAR S, et al. LFM signal detection and estimation based on sparse representation[C]∥Information Sciences and Systems. Piscataway, NJ: IEEE Press, 2015: 1-5.

[5] JIN Y, DUAN P, JI H. Parameter estimation of LFM signals based on scaled ambiguity function[J]. Circuits Systems & Signal Processing, 2016, 35(12): 1-18.

[6] DING Y, SUN L, ZHANG H, et al. A multi-component LFM signal parameters estimation method using STFT and Zoom-FRFT[C]∥IEEE International Conference on Communication Software and Networks. Piscataway, NJ: IEEE Press, 2016: 112-117.

[7] LIU D, LIU Y, CAI H, et al. Linear frequency-modulated continuous wave active sonar signal processing[C]∥OCEANS. Piscataway, NJ: IEEE Press, 2014: 1-5.

[8] 陳小龍, 關(guān)鍵, 劉寧波, 等. 基于FRFT的LFM信號自適應濾波算法及分析[J]. 現(xiàn)代雷達, 2010, 32(12): 48-53.

CHEN X L, GUAN J, LIU N B, et al. Adaptive filtering algorithm for LFM signal and performance analysis based on FRFT[J]. Modern Radar, 2010, 32(12): 48-53 (in Chinese).

[9] 賀達超, 王國宏, 孫殿星. 壓制干擾下長基線雷達網(wǎng)多目標跟蹤技術(shù)[J]. 指揮控制與仿真, 2015(6): 1-7.

HE D C, WANG G H, SUN D X. Multi-target tracking technique for long baseline radar network in the presence of suppressive jamming[J]. Command Control & Simulation, 2015(6): 1-7 (in Chinese).

[10] 王國宏, 李世忠, 白晶, 等. 壓制干擾下組網(wǎng)雷達目標檢測與跟蹤技術(shù)[J]. 宇航學報, 2012, 33(12): 1781-1787.

WANG G H, LI S Z, BAI J, et al. Target detection and tracking technique for radar network in the presence of suppressive jamming[J]. Journal of Astronautics, 2012, 33(12): 1781-1787 (in Chinese).

[11] 李世忠, 王國宏, 白晶, 等. 壓制干擾下雷達網(wǎng)點目標概率多假設跟蹤算法[J]. 西安交通大學學報, 2012, 46(10): 101-106.

LI S Z, WANG G H, BAI J, et al. A tracking algorithm with multiple probabilities hypothesis for radar network point target in the presence of suppressive jamming[J]. Journal of Xi’an Jiaotong University, 2012, 46(10): 101-106 (in Chinese).

[12] 徐海全, 王國宏, 關(guān)成斌. 遠距離支援干擾下的目標跟蹤技術(shù)[J]. 北京航空航天大學學報, 2011, 37(11): 1353-1358.

XU H Q, WANG G H, GUAN C B. Tracking technique in the presence of standoff jamming[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011,37(11): 1353-1358 (in Chinese).

[13] 謝艾彤. 低信噪比信號的檢測與參數(shù)估計方法研究[D]. 成都: 電子科技大學, 2007: 33-35.

XIE A T. Study on detection and parameter estimation of signal in low signal-to-noise ratio[D]. Chengdu: Electronic Science and Technology University, 2007: 33-35 (in Chinese).

[14] 杜東平. 雷達壓制式干擾抑制算法研究[D]. 成都: 電子科技大學, 2008: 24-27.

DU D P. The research of radar pressure jamming suppression algorithm[D]. Chengdu: Electronic Science and Technology University, 2008: 24-27 (in Chinese).

[15] 李智明. 基于改進Fast ICA算法的混合語音盲分離[D]. 上海:上海交通大學, 2015: 21-43.

LI Z M. Blind separation of mixed audio signals based on improved fast ICA[D]. Shanghai: Shanghai Jiao Tong University, 2015: 21-43 (in Chinese).

[16] 齊林, 陶然, 周思永, 等. 基于分數(shù)階Fourier變換的多分量LFM信號的檢測和參數(shù)估計[J]. 中國科學, 2003, 33(8): 749-759.

QI L, TAO R, ZHOU S Y, et al. Detection and parameter estimation of multi-component LFM signals based on fractional Fourier transform[J]. Science in China, 2003, 33(8): 749-759 (in Chinese).

[17] 劉鋒, 徐會法, 陶然. 基于FRFT的對稱三角LFMCW信號檢測與參數(shù)估計[J]. 電子與信息學報, 2011, 33(8): 1864-1870.

LIU F, XU H F, TAO R. Detection and parameter estimation of symmetrical triangular LFMCW signal based on Fractional Fourier transform[J]. Journal of Electronics & Information Technology, 2011, 33(8): 1864-1870 (in Chinese).

[18] 陶然, 鄧兵, 王越, 等. 分數(shù)階傅里葉變換及其應用[M]. 北京: 清華大學出版社, 2009: 11-12.

TAO R, DENG B, WANG Y, et al. Fractional Fourier transform and its applications[M]. Beijing: Tsinghua University Press, 2009: 11-12 (in Chinese).

[19] 張賢達. 信號處理中的線性代數(shù)[M]. 北京: 北京科學出版社, 1997: 65-67.

ZHANG X D. Linear algebra in signal processing[M]. Beijing: Beijing Science Press, 1997: 65-67 (in Chinese).

[20] 張峰, 陶然. 分數(shù)階Fourier域譜估計及其應用[J]. 電子學報, 2008, 36(9): 1723-1727.

ZHANG F, TAO R. Power spectral estimation and its application in Fractional Fourier domain[J]. Acta Electronica Sinica, 2008, 36(9): 1723-1727 (in Chinese).

[21] 王瑜, 李小波, 周青松, 等. 基于FRFT窄帶濾波的LFM信號研究[J]. 火力與指揮控制, 2016, 41(12): 41-43.

WANG Y, LI X B, ZHOU Q S, et al. Study of LFM signal based on FRFT domain narrowband filter[J]. Fire Control & Command Control, 2016, 41(12): 41-43 (in Chinese).

[22] 何友, 修建娟, 張晶煒, 等. 雷達數(shù)據(jù)處理及應用[M]. 北京: 電子工業(yè)出版社, 2010: 117-118.

HE Y, XIU J J, ZHANG J W, et al. Radar data processing with applications[M]. Beijing: Electronic Industry Press, 2010: 117-118 (in Chinese).

[23] 孫殿星. 雷達網(wǎng)抗欺騙式干擾技術(shù)研究[D]. 煙臺: 海軍航空工程學院, 2015: 81-82.

SUN D X. Research on anti-spoofing technology of radar network[D]. Yantai: Naval Aeronautical and Astronautical University, 2015: 81-82 (in Chinese).

[24] 陳小龍, 劉寧波, 王國慶, 等. 基于Radon-分數(shù)階傅里葉變換的雷達動目標檢測方法[J]. 電子學報, 2014, 42(6): 1074-1080.

CHEN X L, LIU N B, WANG G Q, et al. Radar detection method for moving target based on Radon-fractional Fourier transform[J]. Acta Electronica Sinica, 2014, 42(6): 1074-1080 (in Chinese).