隧洞口巖體變形監測與穩定性分析

石立國 鄭 雄 祝 羿

中國建筑第二工程局有限公司 北京 100054

巖體穩定性研究一直是巖土工程領域的基本問題之一，尤其是在眾多坡體失穩等自然災害發生之后，更得到了廣泛的關注，目前巖體變形與穩定性已成為巖土工程中重要的研究方向。

為保證工程安全性，通過監測分析并采取相應的預報控制措施，有利于施工過程中的風險控制。

巖土工程穩定性分析常使用的有極限平衡法和數值計算方法[1-2]，對其變形失穩機制的研究，目前多采用野外監測數據分析、物理模型試驗以及數值模擬分析等方法[3-4]。有限差分數值計算方法，可適用于比較復雜的邊界條件，充分考慮了巖土體的非物質性和不連續性，可以直觀地模擬巖體外部形態和內部介質的變化情況。實體內部介質通過有限差分法，能直觀地顯示實體位移量、應力特征和潛在破裂區等[5-6]，對其穩定性狀況以及易破壞風險區進行預先評判，從而可降低施工中發生事故的概率。

本文將結合數值模擬技術與現場監測方法對隧洞口巖體邊坡的變形特征與安全狀況展開分析和對比，保證施工過程中隧洞與周邊環境的安全。

1 工程地質條件

某水電工程地下電站尾水隧洞出口單級坡比為1∶0.3，巖體主要由灰色薄層灰巖、灰色中厚層灰巖地層構成。巖體邊坡結構為陡傾橫向坡，強卸荷帶水平寬一般為10 m，弱卸荷帶一般為16～25 m。巖體邊坡中部高程950～1 060 m間的緩坡對上部的崩塌塊石有緩沖作用，邊坡上發育的塊體可能影響施工及工程運行安全。右岸尾水出口處巖體巖性復雜，影響范圍內的巖體主要由落雪組第八、九、十段組成。整體圍巖以Ⅱ、Ⅲ類為主，巖體力學參數較好，邊坡表層有淺層強、弱卸荷帶，巖體材料參數相對較差。

2 變形監測分析

隧洞出口巖體坡表面布置有多個監測點，選取6個典型代表性的有效測點TP01～TP06，高程依次分別為962、895、866、956、926、867 m。

由6個表面位移監測點的水平（朝向臨空方向）變形累計值（圖1）可知，近5年來，各部位水平位移均變化不大，最大不超過9 mm，總體的變化規律趨勢具有相似一致性，協調性較好。其中，水平位移最大部位為867 m高程的測點TP06，但位于同樣低高程的測點TP03位移卻相對較小。900 m高程以上的3個測點位移值均較小，變化規律相似，最大不超過5 mm。由此可見，高程高的部位變形相對較小，但水平位移變化與高程并無必然聯系。

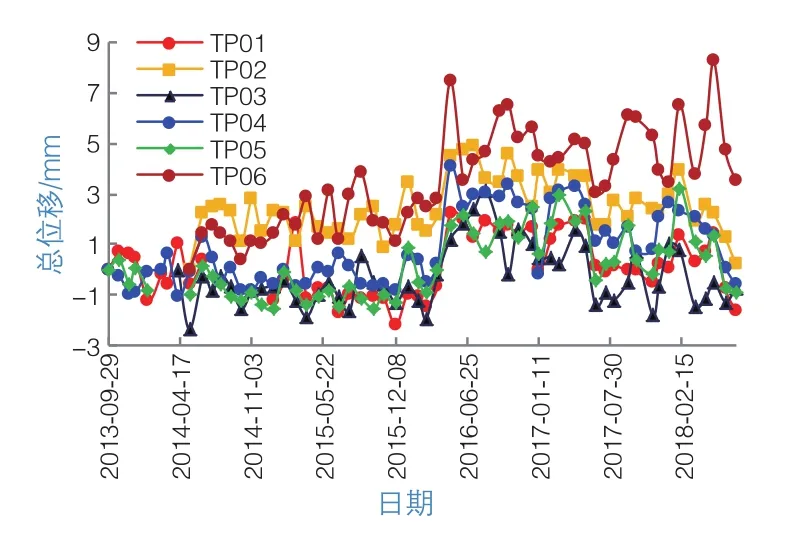
圖1 水平變形累計值

由表面位移監測點的垂直位移累計值（圖2）可知，近5年來，各部位的垂直位移變化總體較平穩，在平穩中逐漸增大，變化規律趨勢具有相似一致性。其中，垂直位移最大部位為866 m高程的測點TP03，最大沉降達15 mm，位于幾乎相同高程的測點TP06沉降也大于其他高程的測點。900 m高程以上的3個測點垂直位移值均較小。

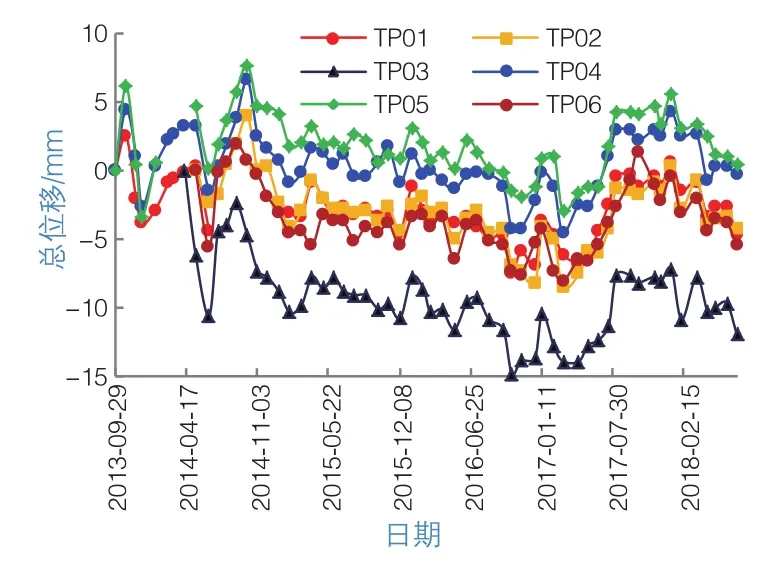
圖2 垂直變形累計值

由此可見，高程低的部位沉降普遍大于高程高的部位。

由表面位移監測點的水平位移月動態改變量（圖3）可知，近5年來，各部位的水平位移處于動態變化之中，處于0值上下變化，基本在－4～4 mm間起伏波動，總體變化平穩，動態變化規律也具有一定的相似性。高程低的點TP06變化相對最大，但月變化量不超過5 mm。

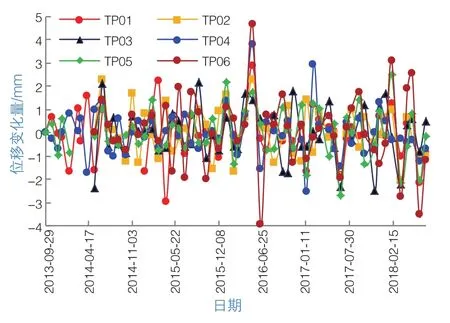
圖3 水平位移月動態改變量

從位移監測數據分析可知，目前位移量值較小，總體變化平穩，無突變、陡增現象，巖體邊坡暫處于穩定狀態。

3 穩定性計算

3.1 計算方法與本構模型

采用Flac3D中Fish語言自編強度折減程序，對穩定性進行有效計算，其中的參數強度折減為：

式中：F——強度參數折減系數；

c、φ——有效黏聚力和內摩擦角；

c'、φ' ——折減后的有效黏聚力和內摩擦角。

本構模型為各向同性彈塑性模型，采用Mohr-Coulomb（M-C）準則，其力學模型為：

式中：σ1、σ3——最大、最小主應力；

f——屈服函數，且f＞0時，材料處于塑性流動狀態，f＜0時，材料處于彈性變形階段，f=0時，處于彈、塑性的臨界狀態。

以上即為剪切破壞判據，拉伸破壞判據為：

式中：σt——巖體抗拉強度。

在有限差分程序中，巖體的體積模量、剪切模量分別由下式計算：

式中：K、G——體積模量、剪切模量；

E——彈性模量；

ν——泊松比。

3.2 數值計算模型建立

根據該區工程地質條件，建立區域三維數值計算模型（圖4）。

計算模型主要包括尾水出口邊坡、尾水隧洞、高導流洞等，坐標原點位于高導流洞出口中心點處，x軸與尾水洞軸線重合，指向尾水洞出口方向為正，y軸從6#尾水隧洞指向4#尾水隧洞為正；z軸與大地坐標系重合，向上為正。模型計算范圍為：268.18 m×230.90 m×339.00 m（x×y×z）。共劃分單元47 665個、節點51 202個。數值計算共分11期開挖，前2期開挖為高導流洞、尾水隧洞間隔開挖，第3～11期為出口邊坡開挖。數值模型各材料參數值如表1所示。

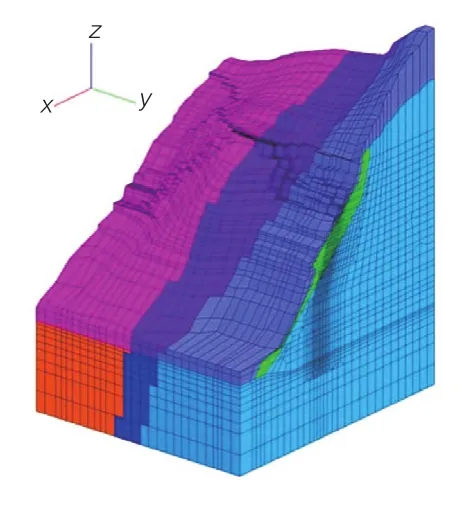
圖4 數值計算模型

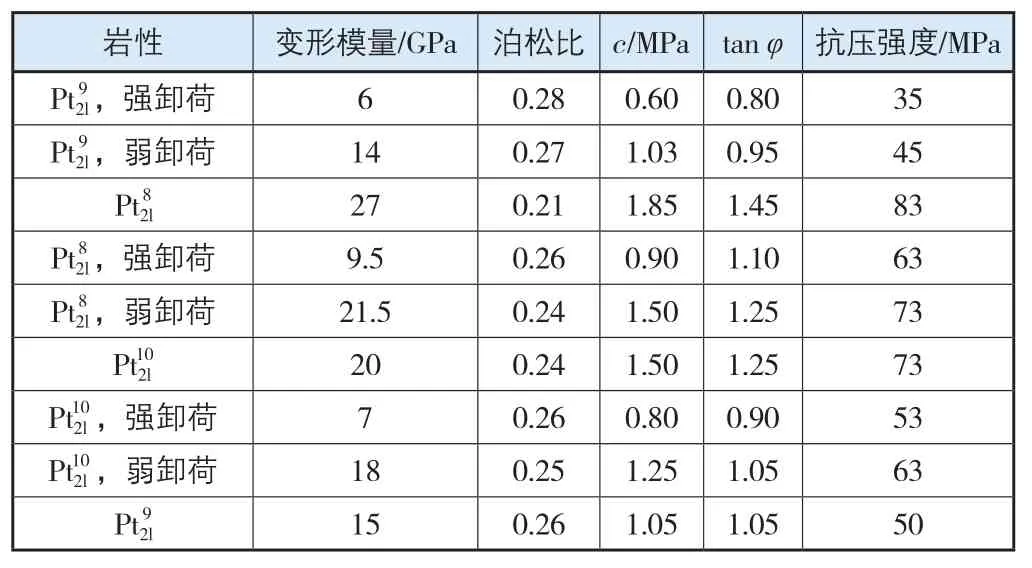
表1 巖體力學參數

3.3 穩定性計算條件

初始地應力場采用自重應力場，其中側壓力系數根據附近地應力測點實測結果綜合比較，選取0.8。采用三維彈塑性有限差分法對整體模型進行穩定性計算分析。計算工況采用以下2種：

1）施工工況：模擬出口邊坡的施工開挖與支護過程，該工況分2種計算方案，分別為無支護和施加系統支護。

2）正常運行工況：分析水庫蓄水后人工邊坡的變形、應力與支護受力情況（水庫正常蓄水位為975 m），下游尾水位為847.86 m。

3.4 施工工況結果分析

破壞區體積總量及破壞區深度如表2、表3所示。由隧洞口破壞區分布（圖5）可知，無支護和有支護方案，邊坡整體破壞區分布規律基本相同，邊坡巖體破壞區主要位于尾水出口洞臉部位。有支護方案邊坡破壞區范圍、深度、破壞總體積較無支護方案有明顯減小，其中開裂區深度最大減小55.0%，塑性區深度最大減小63.4%，破壞總體積減小46.2%。邊坡破壞區主要集中在洞臉部位，最大破壞區深度達9.56 m，位于5#尾水隧洞附近。5#、6#尾水隧洞出口巖柱破壞區貫穿，深度約7 m，在系統錨桿控制范圍內。

由施工期尾水出口邊坡主應力分布計算結果（圖6、圖7）可以看出，相對于無支護條件，錨固支護在一定程度上改善了邊坡巖體的受力情況，第1、3主應力均有一定程度減小，且整個坡體應力分布更為均勻。有支護條件下，邊坡開挖完成后，與初始地應力相比，受開挖卸荷影響在表層強卸荷帶和淺層弱卸荷帶坡體第1主應力有所減小，量值范圍為－1.18～0.08 MPa，主要為壓應力，第3主應力范圍為0.06～0.99 MPa。下部新鮮巖體豎直邊坡段第1主應力較初始地應力有所增大，量值范圍為－3.68～0.08 MPa，第3主應力主要為拉應力，量值范圍為0.06～1.30 MPa，局部出現一定程度的應力集中現象。總體看來，邊坡應力遠小于該部位巖體的抗壓、抗拉強度，因此局部應力集中不會引起邊坡的整體失穩。

表2 施工期不同計算方案邊坡破壞區體積

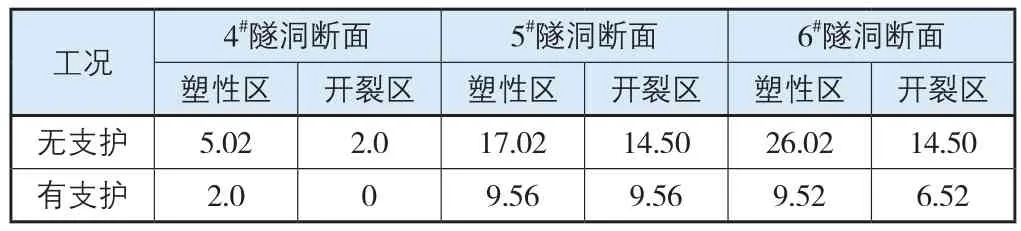
表3 2種支護條件下開挖完畢典型斷面破壞區深度（單位：m）

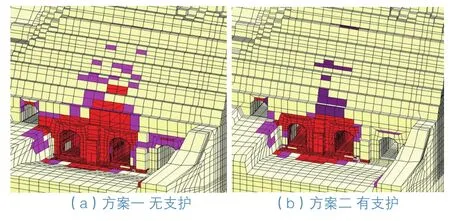
圖5 洞臉邊坡破壞區分布

由巖體位移分布（圖8）可知，不同的計算方案，邊坡巖體的位移分布規律大致相同，從邊坡頂部至底部位移逐漸增大。位移較大處均位于落雪組第九段直立邊坡處。有支護較無支護方案，邊坡變形有明顯減小，其中強卸荷部位坡體變形范圍為0.5～1.7 mm，相應減小約60.5%，弱卸荷部位坡體變形范圍為0.2～5.1 mm，相應減小約50.1%，新鮮巖體斜坡段變形范圍為1.2～7.5 mm，相應減小約47.6%，新鮮巖體豎直坡段變形范圍為2.1～12.1 mm，相應減小約34.9%。可見，噴錨支護對邊坡變形有較好的限制作用，整體邊坡支護參數較為合理。

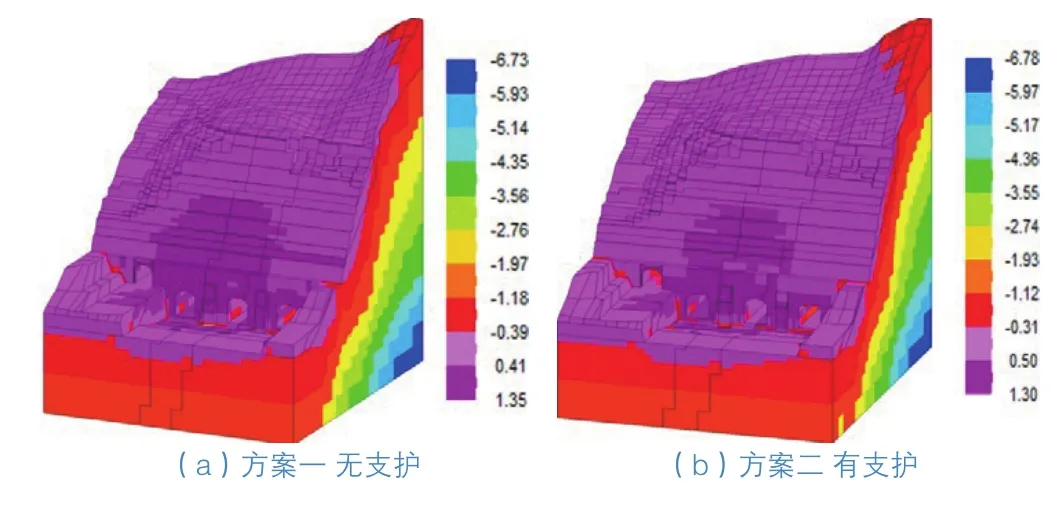
圖7 施工期第3主應力分布云圖

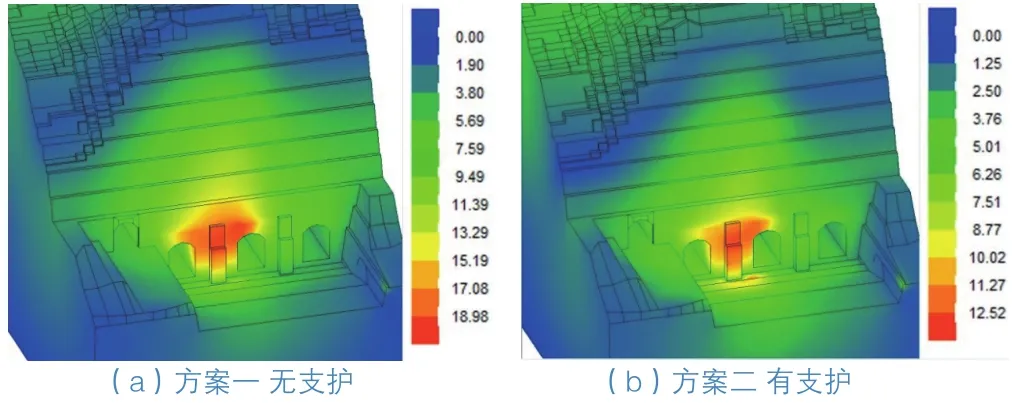
圖8 施工期位移分布云圖

3.5 正常運行工況結果分析

正常運行期，區域巖體破壞區分布規律與有支護開挖完畢時基本相同。相對于無支護情況，直立邊坡塑性區大部回彈，且大量開裂區調整為塑性區，開裂區深度減小達50%。總破壞體積比有支護條件減小約19.8%。

與施工期相比，邊坡上部應力基本相當，下部第1主應力范圍為－3.25～0.32 MPa，第3主應力范圍為0.06～1.06 MPa。最大壓應力為－3.92 MPa，最大拉應力為1.20 MPa，均出現在隧洞出口附近，邊坡第1主應力壓應力值不大，拉應力值也遠低于邊坡巖體的極限抗拉強度。

運行期邊坡上部斜坡段位移在8.0 mm以內，最大位移為11.1 mm，出現在5#、6#隧洞洞臉處。

運行期邊坡錨桿應力范圍為0.1～60.5 MPa。相對于施工期，正常運行工況錨桿應力略有減小，最大錨桿應力值為60.5 MPa，比施工期減小約2.3 MPa，最大錨桿應力出現在5#、6#隧洞。邊坡錨索應力范圍為1 016.9～1 025.4 MPa。總體而言，錨桿、錨索應力水平較低，均在設計強度范圍內。綜上所述，可以認為，該導流隧洞出口邊坡開挖、支護設計合理，巖體邊坡整體穩定性較好。

4 結語

1）通過多年實測變形數據分析，隧洞出口邊坡巖體變位平穩，總體正常，沒有出現位移突變的跡象。

2）通過對比數值分析和實測數據結果，模擬反饋結果與監測數據具有良好的一致性，驗證了利用有限差分法開展巖體變形與安全分析的合理性和可行性。

3）通過有限差分數值計算法對隧洞出口巖體邊坡穩定性進行數值模擬和分析評價，預測潛在易破壞區，具有較好的效果，且有限差分數值計算方法考慮了巖土體的非線性大變形，克服了傳統極限平衡分析和有限元法的不足。