基于禁忌動態規劃的含電動汽車機組組合研究
梁 捷
(中國南方電網廣西電網有限責任公司電力科學研究院,廣西 南寧 530023)
0 引言
大規模電動汽車(electric vehicles,EV)接入電網將會對電力系統的規劃、運行及市場運營產生巨大影響,考慮EV入網后的機組組合問題(unit commitment,UC),需要在UC模型中體現EV的充電放電行為,實現EV及傳統機組的綜合調度,使系統總運行成本最小[1]。UC問題中目標函數的非凸、非線性以及復雜嚴格的約束使得該問題難以求得全局最優解。常見方法包括優先順序法[2],動態規劃法[3],分支定界法[4],混合整數規劃法[5],遺傳算法[6]等。這些方法存在著易陷入局部最優或在應用于大規模系統時會遇到維數災等問題。
文獻[7]采用一種混合優化算法求解UC問題,它將原問題分解成僅含狀態變量的組合和含機組有功出力的非線性規劃2個子問題,用禁忌搜索算法(tabu search,TS)求解組合子問題,粒子群和序列二次規劃混合法求解非線性規劃子問題,仿真表明如此可改善TS算法的收斂速度和搜索能力。文獻[3]提出了基于優先順序法的動態規劃法(dynamic programming,DP),可提高計算速度,但該法對大規模UC問題常常找不到質量較好的解。文獻[8]提出了一種計及EV充電需求的電力系統機組組合模型,把滿足EV充電需求納入約束條件,但缺乏大規模系統和多算法間的性能比對研究。
為了在可接受的時間內得到優質解,文中提出一種用于UC問題的禁忌動態規劃法。在傳統前向動態規劃法的基礎上,根據路徑存優指標對訪問路徑集進行局部存優,并引入禁忌搜索進行狀態訪問控制。此外,提出一種基于試停優化的壓縮狀態空間的構造法。最后對10機組24時段及其拓展系統進行仿真,進行文中算法的有效性驗證和多算法間的性能比對研究。
1 含電動汽車機組組合問題模型
以機組總發電成本最低為優化目標[9]。
(1)
式中:Pi,t為第i臺發電機組第t時段的出力;ui,t為第i臺發電機組第t時段的狀態,當其處于運行狀態時為1,否則為0;xoffi,t為第i臺發電機組第t時段的累計已停機時間;fi為第i臺發電機組的燃料成本函數;Qi,t為第i臺發電機組第t時段的啟停成本函數[9];Nu為發電機組總數;T為總優化時段。約束條件為:
(1) 系統功率平衡約束。
(2)
式中:PLDt為第t時段系統的基線負荷水平;PEVj為第j輛EV的充電功率;vj,t代表第j輛EV在第t時段是否處于充電狀態,是則為1,否則為0;NEV為并入電網的EV數[10]。
(2) 旋轉備用約束。
(3)
式中:Pmaxi為第i臺機組的出力上界;Rt為時段t的備用需求。
(3) 機組有功出力約束。
ui,tPmini≤Pi,t≤ui,tPmaxi
(4)
式中:Pmini為第i臺機組的出力下界。
(4) 最小啟停時間約束。
發電機狀態從開機到停機:
(xont,i-Toni)(ui,t-ui,t+1)≥0
(5)
發電機狀態從停機到開機:
(xofft,i-Toni)(ui,t+1-ui,t)≥0
(6)
式中:xont,i為第i臺發電機組在第t時段連續運行的時間;Toni,Toffi分別為第i臺發電機組的最小允許開機和停機時間。
(5) 爬坡約束。
-Pdowni≤Pi,t-Pi,t-1≤Pupi
(7)
式中:Pupi,Pdowni分別為機組i的功率上升量限制和功率下降量限制[10]。
(6) EV用戶充電需求約束。
為了滿足EV充電需求,需要滿足如下蓄電池電量關系:
SjOC-need≤SjOC-td≤1
(8)
式中:SjOC-td表示第j輛EV在離網時的電池荷電狀態(%);SjOC-need表示第j輛EV在離網時所期望達到的電池荷電狀態(%),電池各個時刻的電量存在以下遞推公式[10]:
(9)
式中:SjOC-t表示時刻t的EV電池荷電狀態;η為充電效率;Cj為電池容量;ΔT表示計算時間步長,單位為h。
(7) 充電時間約束。
toj≤tj≤tdj-1
(10)
式中:toj,tdj分別為第j輛電動汽車開始并網時刻和離網時刻;tj為給第j輛電動汽車充電的時刻。該式對智能充電方案下的電動汽車的充電時間進行了約束,表明只有在電動汽車并網之后、離網之前,才可以根據電網側和用戶側的雙重需求進行調控[11]。上述式(1—10)組成的優化模型為非線性混合整數規劃問題。為便于求解,對模型的目標函數及約束條件進行部分線性化[5]。
2 禁忌動態規劃算法
2.1 基于局部存優的前向動態規劃法
動態規劃算法是一種用于多階段決策問題的優化方法[12-13]。前向動態規劃法(forward dynamic programming,FDP)首先定義t時段狀態空間St為該時段所有可能的機組開停和EV充電狀態的組合,優化時從初始階段開始,在相應的空間中逐一訪問各狀態,按式(2)從前到后依次計算到達各階段各狀態的值函數:
Vt,JP(St)=Ct(St,fi,Qi,t)+Vt-1,JP(St-1)
(11)
式中:JP表示當前時段滿足約束條件的轉移路徑,即可行狀態集;Vt,JP(St)為值函數,表示從初始狀態到t時段狀態的總發電成本;Ct表示從t-1時段的狀態轉移到t時段狀態的轉移成本,為Fc的子集。
然后記錄到達當前狀態的路徑,再從末時段累計轉移成本最小的路徑對應的狀態開始,從時間上逆序回溯剛才的過程。依次記錄各階段使總的累計轉移成本最小的狀態,最后得到的狀態集就是所求機組開停和EV充電狀態的優化方案[11]。可見,若用FDP求解含N臺機組,T個調度時段的UC問題,若不限制狀態數,則各時段狀態空間中狀態數為2N個,而JP共有(2N)T種。當N和T增大時,計算量和所需的存儲空間將急劇增加,造成所謂的“維數災”問題。
對此,文中給出基于試停優化的狀態生成法和局部存優策略,分別從狀態空間的初始化和FDP的狀態訪問過程控制狀態空間的膨脹。
局部存優策略是在算法遍歷各時段時只根據路徑存優指標(path optimization index,POI)大小排序,并擇優保存有限條路徑,如此,每次迭代僅需考慮少量路徑,如此可減少各時段需要考慮的狀態數和時段間的轉移路徑數[12]。
POI綜合考慮機組在最大出力下的單位燃料成本和為后續時段提供的旋轉備用容量裕度,定義如下:
(12)
式中:δ為權重系數,IPOI值越大,代表路徑對應方案的經濟性越好。
針對大規模UC問題中枚舉法生成的初始狀態空間規模較大的問題,文中按試停優化的方式生成初始狀態空間,步驟如下:
(1) 在各時段狀態空間中分別構建(NG+1)個試停調度子問題如下。
(13)
其中,在第i個該問題中,關閉第i臺機組,開啟其他機組,則可得NG個方案,考慮到峰值時段負荷需求較大,額外增加一個開啟所有機組的方案。
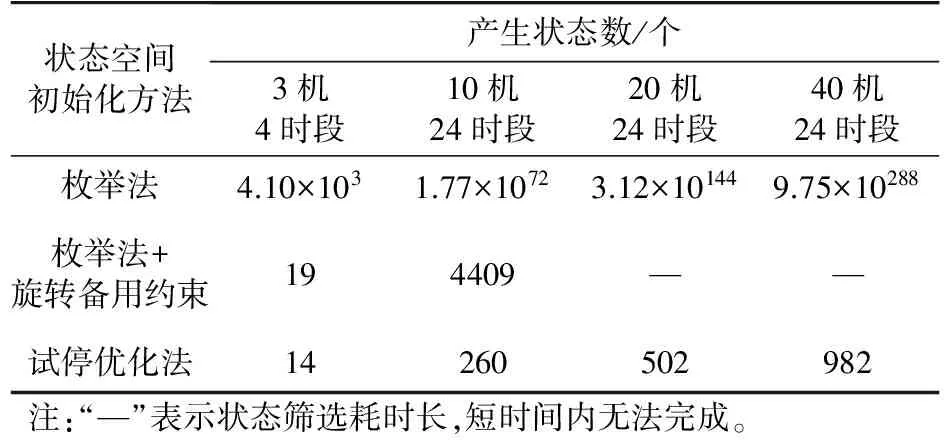
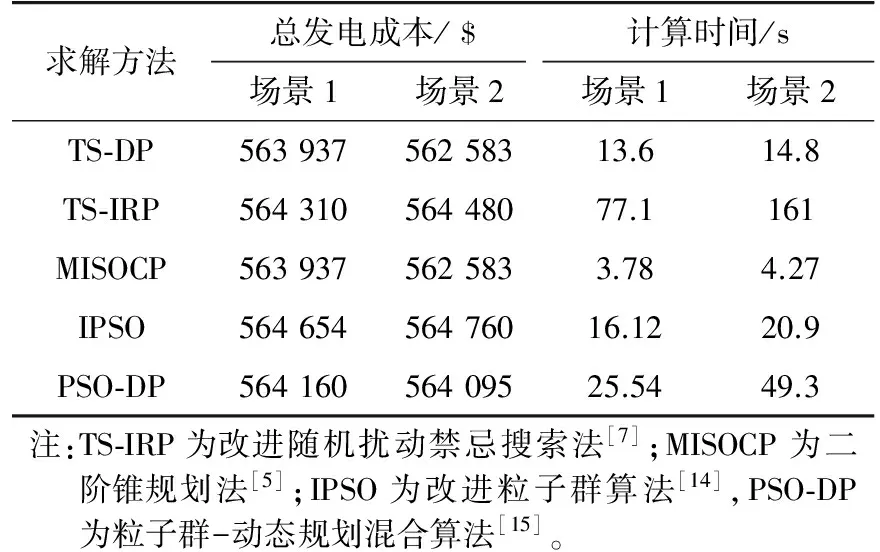
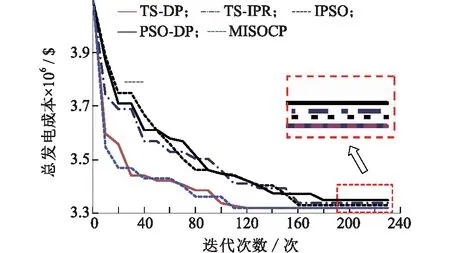
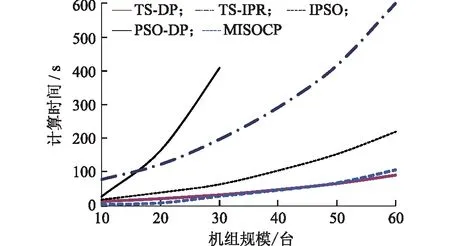
(2) 式(13)以每個初始機組啟停方案的運行成本最小為目標進行優化,根據優化結構對(1)中的方案進行調整:若ui,t=1,且Pi,t (3) 根據式(3)校驗(2)所得方案是否滿足旋轉備用約束,若不滿足,就用優先順序法[2]作進一步鄰域調整,最后除去重復狀態得到調整后的狀態空間。 若2.1節方法在一次路徑搜索找不到滿意解,則需構建推動路徑轉移進行迭代搜索的機制,此外,該方法具有貪婪性質,它在決策過程中未能全局考慮時段間的約束條件,且易陷入局部極值。對此,引入了禁忌搜索算法中的禁忌列表(tabu list,TL),通過構建記憶結構來引導路徑搜索,過程為:首先在歷史搜索過程中選擇禁忌對象更新TL,阻止算法重復訪問該狀態,然后在遍歷各時段時從TL以外的狀態中擇優訪問其他狀態,從而推動路徑在鄰域內局部修正,得到新的轉移路徑,再根據路徑存優指標進行路徑篩選[12]。重復上述過程直到得到滿意解或達到迭代次數上限。 禁忌對象是組成TL的元素,考慮到小容量的調峰機組在負荷峰值及其臨近時段(Tp)易形成多種組合路徑,而2.1節的方法缺少局部精細搜索能力,故禁忌對象sTB按如下方式選擇: (14) 在FDP過程中,在某個時段可能會出現當前狀態空間中的狀態均不可行的情況,即陷入“死路”。對此,定義解禁規則為:在該情況下,將當前路徑的前一個時段的狀態列入TL,同時解禁當前時段所有被禁忌對象,即當前時段的TL重新初始化,最后終止本次迭代。如此下一次迭代可避開這條路徑上的不可行的狀態節點。 應用文中算法對10—60機組24時段系統在MATLAB環境進行仿真計算,火電機組和負荷數據參見文獻[8]。電動汽車集群總容量占基線負荷總量的比值為10%,充電模式為分時電價政策間接引導模式,即在負荷低谷期通過降低電價來引導用戶在低谷期充電,起到一定的填谷作用。電動汽車的電池容量等參數及電價方案見文獻[8]。 表1比較了3種壓縮方式下4個系統中生成的狀態數,數值大的數以科學計數法表示并保留2位小數。其中方法1為通過枚舉法獲得的所有狀態總數,可通過2.1節的方法得到。方法2為在機組最大出力時根據旋轉備用約束排除不可行的狀態后剩下的狀態數,由于需逐個根據式(3)計算,大規模系統短時內難以求出。方法3為文中基于試停優化方式獲得的狀態數。由表1可見,方法1的規模隨機組和時段數的增加而呈級數式劇增。方法2根據約束條件壓縮后規模減小,但在后2個規模稍大的系統時仍會遇到維數災問題。本文方式能有效壓縮狀態數,生成規模較小的初始狀態空間。 表1 3種狀態空間的初始化方法比較Tab.1 Comparison of initialization methods for three kinds of state spaces 表2比較了對10機組算例,文TS-DP法和其他5種算法的計算結果。場景1為不考慮爬坡約束和EV接入,場景2考慮爬坡約束和EV接入。對比表中的5種方法,包括同樣用到禁忌思想的TS-IRP,用到動態規范法的PSO-DP,以及用到割平面信息的MISOCP。可見TS-DP求得的總發電成本與MISOCP一致,為表中最小,計算速度優于基于隨機搜索的TS-IRP算法。由于MISOCP采用同倫內點法求解,同倫初值和梯度下降技術的應用使該算法在較小的狀態空間能快速逼近目標解,而本文方法需經歷試停優化子問題求解,狀態訪問和篩選等過程,故在小規模系統中計算速度稍慢于該方法。此外,場景2考慮爬坡約束和EV接入后,計算速度方面,約束和變量數的增加使得各算法的計算時間均被延長。優化效果方面,由于電動汽車是按比例滲透入基線負荷內,故雖然整體負荷水平不變,但通過電價引導電動汽車充電行為后,電動汽車會主要集中于電網谷時段充電,使負荷曲線平滑化[16-17],從而為各時段的機組啟停和出力的調整提供更寬裕的環境,調度方可通過增加經濟型機組出力、減少耗費型機組出力的方式來降低發電成本,故TS-DP、PSO-DP和MISOCP在場景2的總發電成本均低于場景1。TS-IRP和IPSO的成本反而增加,這是由于場景2增加爬坡約束和EV約束后使得UC問題的解空間更為復雜,TS-IRP和IPSO的全局搜索能力較弱,在該環境下易被局部極值吸附。 表2 10機組系統計算結果比較Tab. 2 Comparison of calculation results of 10 unit 圖1為60機組系統算例不同方法迭代過程中目標函數下降曲線。由圖1知,IPSO、TS-IRP和PSO-DP算法在迭代前期(約在20~40次迭代時)便呈現停滯現象,表明陷入了局部極值,而TS-DP算法和MISOCP算法在迭代早期目標函數下降較快。TS-IRP、PSO-DP和IPSO算法在迭代后期下降速度變慢,說明其全局搜索能力較弱,終止時得到的優化結果均劣于TS-DP和MISOCP算法。TS-DP算法由于禁忌列表的存在,算法可有效避免迂回搜索,使目標函數在整個迭代過程能得到持續優化,故其全局搜索能力和局部搜索能力均較強。MISOCP是一種在每次迭代時通過構造最小覆蓋不等式形式的二階錐約束獲取更緊的解集的解析算法,對優化問題原本的凸性影響較小[5],在有限的迭代次數內比上述隨機優化算法能進行更徹底的全局搜索,故其優化結果與本文TS-DP算法接近,優于其他3種算法。 圖1 不同方法迭代過程中目標函數下降曲線Fig. 1 decline curve of objective function in iterative process of different methods 圖2給出10機組系統在場景1時3種方法的計算結果比較。可見,TS-IRP、PSO-DP和IPSO法受“維數災”影響較大,計算時間隨機組數劇增,其中增幅最大的是用到動態規劃的PSO-DP算法,為便于觀察只給出其10—30機組的計算時間,40—60機組的計算時間與另5個方法差距較大,故從略,這是由于PSO-DP仍保留了動態規劃窮舉搜索路徑的搜索思路,盡管通過粒子群算法對搜索空間進行隨機壓縮,但效率不高。本文TS-DP算法10—40機的計算速度慢于MISOCP算法,50和60機組的計算時間與MISOCP相差不大,但TS-DP的計算時間隨機組數增長的增加趨勢較為平緩一些。這是由于MISOCP每次迭代需要更新二階錐割集,當約束數較多或變量維數較大時,該割集的各階偏導數和矩陣矢量積計算的運算量將呈級數式劇增,雖然通過多面體線性近似簡化計算[5],但從圖2來看效果有限。而TS-DP分別通過試停優化和局部存優方式控制初始狀態空間和搜索路徑集規模,故計算量受機組數影響較小。 圖2 不同方法計算時間與機組規模的關系Fig. 2 The relationship between the number of the units and CPU time for different methods 研究了含電動汽車的機組組合模型,針對應用動態規劃求解大規模機組組合問題時的“維數災”困難,構建了禁忌動態規劃法。在采用根據機組單位燃料成本和旋轉備用容量裕度對訪問路徑集進行局部存優,減少了路徑評估的計算量。減少了傳統前向動態規劃需要保存的狀態和決策數。為避免改動后的算法陷入局部極值,引入禁忌搜索算法中避免重復訪問某些歷史過程的思想,通過設置禁忌列表,防止路徑的迂回搜索。此外,提出壓縮狀態空間的構造方法,在搜索前結合UC問題的特點縮減了初始狀態空間的規模,使其隨機組數量增加呈線性增長。 10—60機組算例仿真結果表明,文中的方式能有效壓縮狀態數,生成規模較小的初始狀態空間。TS-DP算法不易陷入局部極值,能獲得質量較好的次優解且受維數災的影響較小,驗證了其可行性,但其魯棒性也有待進一步的提高。 參考文獻: [1] 張軍,韓華春,原增泉. 基于兩級充電管理系統的電動汽車智能充電控制系統研究[J]. 電力工程技術, 2017(5):86-92. ZHANG Jun, HAN Huachun, YUAN Zengquan. Smart charging electric vehicles based on two-level charge management system[J]. Electric Power Engineering Technology, 2017(5):86-92. [2] 李利利,丁恰,涂孟夫,等. 機組組合問題的仿射可調整魯棒優化模型與算法[J]. 電力工程技術, 2017, 36(3):33-37. LI Lili, DING Qia, TU Mengfu, et al. Affine adjustable robust optimization model and algorithm for unit commitment problem[J]. Electric Power Engineering Technology, 2017, 36(3):33-37. [3] 任垚,張小青. 基于改進動態規劃法的電力系統機組組合問題研究[J]. 自動化技術與應用, 2010, 29(5):6-8. REN Yao, ZHANG Xiaoqing. Improved dynamic programming method of power system unit commitment problem research and application based on [J]. Techniques of Automation and Application, 2010, 29 (5): 6-8. [4] 宋瀟,李葉,劉家軍,等. 基于改進粒子群文化算法的機組組合聯合調度研究[J]. 電網與清潔能源, 2016, 32(6):77-84. SONG Xiao, LI Ye, LIU Jiajun, et al. Improved cultural particle swarm algorithm unit combination scheduling of [J]. Power System and Clean Energy, 2016, 32(6): 77-84. [5] 全然,韋化,簡金寶. 求解大規模機組組合問題的二階錐規劃方法[J]. 中國電機工程學報, 2010, 30(25): 101-107. QUAN Ran, WEI Hua, JIAN Jinbao. Solution of large scale unit commitment by second-order cone programming[J]. Proceedings of the Chinese Society of Electrical Engineering, 2010, 30 (25): 101-107. [6] 田洋,段文超,孫凱. 基于蜜蜂進化型遺傳算法的機組組合研究[J]. 數字技術與應用, 2013(2):113. TIAN Yang, DUAN Wenchao, SUN Kai. Research on unit commitment based on bee evolutionary genetic algorithm [J]. Digital Technology and Application, 2013(2): 113. [7] VICTOIRE T A A, JEYAKUMAR A E. Unit commitment by a tabu-search-based hybrid-optimization technique[J]. IEEE Proceedings-Generation, Transmission and Distribution, 2005: 563-574. [8] 陳彬,王業磊,許昭,等. 計及電動汽車充電調度可行域的電力系統機組最優組合[J]. 華北電力大學學報(自然科學版), 2014, 41(1):38-44. CHEN Bin, WANG Yelei, XU Zhao, et al. Optimal combination of power system units considering feasible areas of electric vehicle charging scheduling [J]. Journal of North China Electric Power University (Natural Science Edition), 2014, 41 (1): 38-44. [9] 崔微,趙君,白莉紅. 基于多智能體的混合發電機組調度問題研究[J]. 陜西電力, 2014, 42(4):74-77. CUI Wei, ZHAO Jun, BAI Lihong. Multi agent scheduling problem of hybrid power unit based on [J]. Shaanxi Electric Power, 2014, 42 (4): 74-77. [10] 吳可,汪春,孫海順,等. 含大規模電動汽車的電力系統機組組合問題研究[J]. 電力建設, 2014, 35(12):26-31. WU Ke, WANG Chun, SUN Haishun, et al. Study on unit commitment of power system with large scale electric vehicles [J]. Electric Power Construction, 2014, 35 (12): 26-31. [11] 史國青. 火電廠機組負荷優化組合分配問題的研究[D]. 北京:華北電力大學, 2005. SHI Guoqing. Study on optimal allocation of unit load in thermal power plant [D]. Beijing:North China Electric Power University , 2005. [12] 梁捷. 基于禁忌動態規劃的電力系統最優機組組合問題研究[D]. 南寧:廣西大學, 2013. LIANG Jie. Study on optimal unit commitment of power system based on tabu dynamic programming [D].Nanning:Guangxi University, 2013. [13] 陳夢濤,陳衛,李世龍,等. 電動汽車充電站多階段規劃[C]∥中國高等學校電力系統及其自動化專業學術年會. 2014. CHEN Mengtao, CHEN Wei, LI Shilong, et al. Muti-stage planning for electric vehicles charging station[C]∥Academic Annual Meeting of Electric Power System in China. 2014. [14] GOMEZ-GONZALEZA M , LóPEZB A, JURADOA F. Optimization of distributed generation systems using a new discrete PSO and OPF[J]. Electric Power Systems Research, 2012,84(12):172-180 [15] CHAKRABORTY S, SENJYU T, YONA A, et al. Thermal generation planning strategy facilitating units decomposition by particle swarm optimization and multi-stage dynamic programming[C]∥Transmission and Distribution Conference and Exposition: Asia and Pacific, 2009, 1-4. [16] 張靜,湯奕,陳成,等. 考慮分時電價和系統峰谷差動態約束的電動汽車有序充電策略[J]. 電網與清潔能源, 2014(5):79-84. ZHANG Jing, TANG Yi, CHEN Cheng, et al. The orderly charging strategy of electric vehicles considering the dynamic constraints of TOU price and system peak valley difference [J]. Power Grid and Clean Energy, 2014 (5): 79-84. [17] 劉青松,王瑞明,王斌,等. 基于思維進化算法的滑模控制感應電機伺服驅動系統研究[C]∥中國控制會議. 2008. LIU Qingsong, WANG Ruiming, WANG Bin, et al. Research on sliding mode control induction motor servo drive system based on thought evolution algorithm[C]∥China Control Conference.2008.2.2 基于禁忌思想的狀態轉移過程
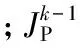
3 算例分析
5 結語

