基于點估計法的桿塔結構平均可靠度分析

黃　興， 田　雷， 楊　洋，廖邢軍， 蒲　凡， 李　鐘

(1． 西南電力設計院有限公司，四川 成都 610021；2． 國網北京經濟技術研究院，北京 102209)

0　引言

由于不可避免的隨機性，可靠度成為結構設計的基礎，實用設計表達式則是可靠度在結構設計中最直接的體現。然而，對輸電塔桿塔結構而言，其可靠度與規范的目標可靠指標并不一定相同，究其根源，主要原因在于：目前輸電塔結構設計規范基本上是參照建筑結構規范進行編制的[1]，而建筑結構規范中所涵蓋的設計對象大多針對荷載效應比不大于3的情況[2]。然而，對于輸電塔結構，其桿塔的自重較輕，承受的活荷載較高，導致其荷載效應比往往高于一般結構構件。當荷載效應比較高時，按照實用設計表達式設計出的構件可靠度水平則會降低。為研究輸電塔桿塔構件荷載效應比對其可靠度水準的影響，許多專家學者對現有輸電塔規范的可靠度水平進行了校準。馮云芬等[3]考慮恒荷載與風荷載的簡單組合，研究了風荷載效應比變化范圍為0.1～100時可靠度水準的變化；李峰等[4]研究了風荷載效應比為4.0～8.0的可靠度水準平均值；王松濤[5]則計算了風荷載效應比范圍為4.0～10.0的可靠度指標平均值；劉靜波[6]研究了風荷載效應比1.0～40.0范圍內可靠度指標的變化，并得到可靠度指標的平均值。可以看出，現有研究的一般做法為：先假定荷載效應比的取值范圍，再在該范圍內選取多個離散的荷載效應比值，計算這些離散點處的可靠度指標，并計算這些可靠度指標的平均值。然而，荷載效應比范圍的設定以及離散點的選取過于主觀，得到的可靠指標平均值不具有統計意義。因此，如何全面客觀地考慮荷載效應比的取值，是研究荷載效應比對可靠度水準影響的關鍵。

為此，文中首次嘗試將荷載效應比視為隨機變量，沿用點估計法的基本思想，以荷載效應比的分布為輸入，得到基于荷載效應比分布的、具有統計意義的桿塔結構加權平均可靠度指標。

1　荷載效應比分布擬合

1.1　樣本點選取

不失一般性，文中選取恒荷載+風荷載簡單組合(下稱恒風組合)下的軸心受壓桿件為例，其它荷載組合下不同受力方式桿件的分析可依次類推。軸心受壓桿件的風荷載效應比ρW的計算公式為：

(1)

式中：NWk為風荷載引起的桿件軸心壓力標準值;NGk為恒荷載引起的桿件軸心壓力標準值;NW為風荷載引起的桿件軸心壓力設計值;NG為恒荷載引起的桿件軸心壓力設計值;γQ為活荷載分項系數;γG為恒載分項系數。

文中選取安徽到上海某條實際輸電線路工程，并統計如表1所示8個不同工況下的直線塔的風荷載效應比。實際桿塔設計中，部分按照構造要求設計的輔材和按照統材要求設計的桿件不由設計表達式控制。綜上所述，文中基于道亨軟件，僅選取應力百分比大于50%的桿件作為風荷載效應比的有效樣本進行統計分析，樣本點共計1253個。

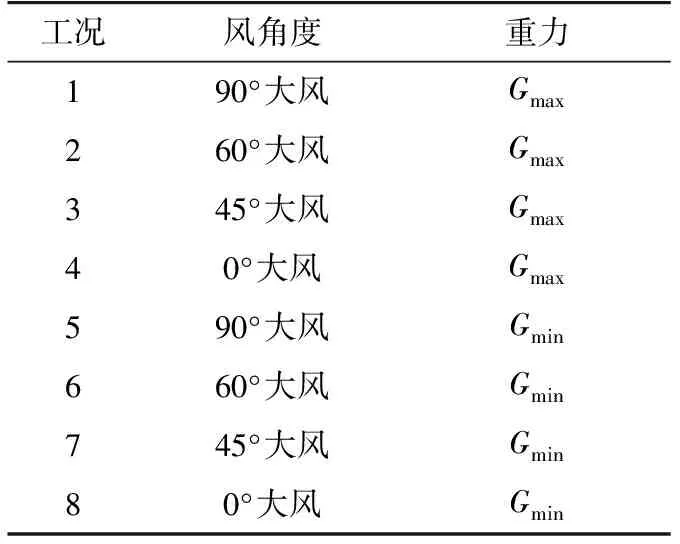
表1　工況選取Tab.1　Working conditions selected

其中，大風代表施加風速為30 m/s的風荷載；Gmax為重力荷載不利工況；Gmin為重力荷載有利工況。

1.2　分布擬合

基于以上樣本，進而對樣本的總體分布進行擬合。文中采用MATLAB軟件的分布擬合工具箱近似得到總體分布密度函數曲線[7- 9]，共選取7種不同分布類型進行擬合，選用分布類型如表2所示。

表2　選用分布及簡稱Tab.2　Distributions used andthe corresponding abbreviations

根據上述7種分布類型進行分布擬合，可以得到如圖1所示的概率密度函數的擬合，以及如圖2所示的累計分布函數的擬合。

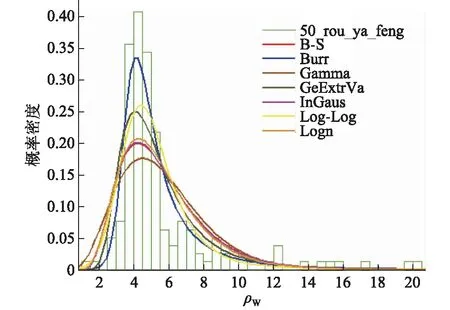
圖1　風荷載效應比的概率密度函數Fig.1　PDF of wind load effect ratio

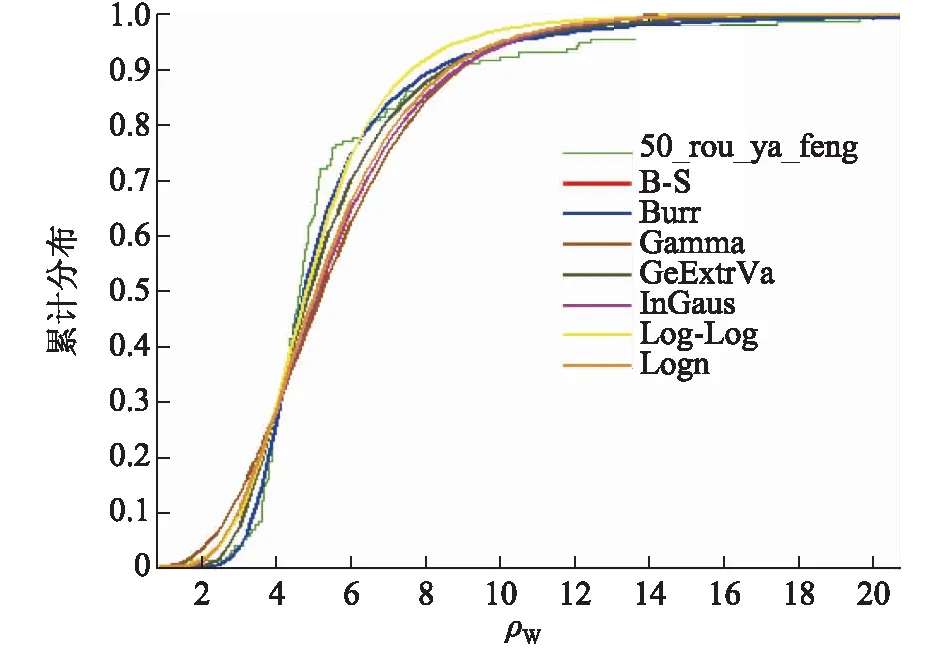
圖2　風荷載效應比的累計分布函數Fig.2　CDF of wind load effect ratio

通過對比7種不同的分布，文中選取其中擬合程度較好的Log_Logistic分布，對應的均值和標準差分別為5.556 2和4.659 9。

2　基于點估計法的可靠度指標均值

2.1　功能函數的建立

DL/T 5154—2012架空送電線路桿塔結構設計技術規定[10]關于鐵塔結構承載能力極限狀態的設計表達式，是根據GB 50068—2001建筑結構可靠度設計統一標準的有關原則確定的。在結構可靠度分析中，結構的極限狀態可由其功能函數來表達，功能函數形式為[11]：

Z=g(X1,X2,…,Xn)

(2)

式中：X=[X1，X2，...，Xn]為工程結構中存在的各種不確定信息的隨機變量。從性質上來說，可以分為結構參數和荷載參數2類：第一類是結構抗力，用R表示；另一類是荷載的作用或作用效應，用S表示。當僅以荷載效應S、結構構件抗力R作為2個基本隨機變量時，功能函數可表示為：

Z=g(R,S)=R-S

(3)

當Z<0時，結構處于失效狀態；當Z>0時，結構處于可靠狀態；當Z=0時，結構處于極限狀態。

文中僅選取恒風組合下桿塔結構中軸心受壓構件進行可靠度校準，其對應的功能函數為[12]：

Z=R-SG-SW

(4)

式中：R，SG，SW分別為輸電塔桿塔構件的抗力隨機變量、恒載隨機變量和風荷載隨機變量。

為計算式(4)的可靠度，需要得到上述隨機變量的統計參數和分布類型。其中，值得注意的是，隨機變量的均值由變量標準值乘以均值系數得到。

不失一般性，假設SGk=1，SWk=ρW[12]。對于桿塔結構的實用設計表達式，李峰等[7]在規范基礎上考慮了導線線條風荷載調整系數和不同重現期基本風壓換算系數的影響；王松濤等[5]進一步考慮了最小設計風速影響系數的影響。然而，已有研究并未考慮檔距利用率和截面利用率的影響。因此，文中所采用的實用設計表達式在已有研究的基礎上進一步引入了檔距利用率和截面利用率，抗力標準值Rk如下式所示：

Rk=γ0γRγA{γG(SGk)+
γQ[βv((1-χ)SQk+βcχSQk/γ檔距)]}

(5)

式中：γ0為結構重要性系數；γ檔距為檔距利用率，根據實際經驗取1/0.9；γR為抗力分項系數；γA為截面利用率，根據實際經驗取1/0.95；γG為恒載分項系數；γQ為可變荷載分項系數；SGk為永久荷載標準值；SQk為風荷載標準值；Rk為結構構件的抗力標準值；βv為最小設計風速影響系數，βc為導地線風荷載調整系數，βv和βc的取值見表3；χ為線條風荷載效應占風荷載總效應的比值，根據相關文獻[3-5]和工程經驗，取值范圍為0.2～0.4。

表3　最小設計風速影響系數βv及導地線風荷載調整系數βcTab.3　Value of βv and βc

將SGk=1，SWk=ρW代入式(15)中，可進一步得到：

RK=γRγ0γA{γG+aρW}F(ρW)

(6)

式中：a=γQ{βv[(1-χ)+βcχ/γ檔距]}。

綜上所述，式(4)中隨機變量的分布參數和分布類型如表4所示[5]。

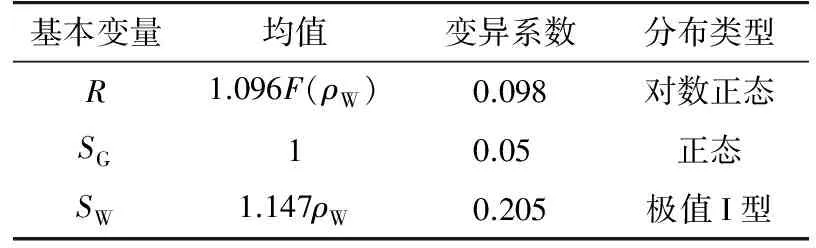
表4　基本隨機變量的統計信息Tab.4　Statistical information of basic variables

2.2　基于點估計法的平均可靠指標計算

通過上述分析可知，基本隨機變量的統計參數是荷載效應比ρW的函數，當荷載效應比ρW確定時，即可利用JC[11]法求解式(4)的可靠指標β。因此，可靠指標β可以表達為荷載效應比ρW的隱式函數，如式(7)所示:

β=f(ρW)

(7)

式中：f(．)表示β與ρW的關系，為隱式函數。對于任一給定的ρW，β可方便地由JC法確定[13]。進而，可靠度指標的均值可表示為:

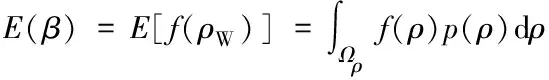
(8)

式中：Ωρ為ρ的取值域；p(．)表示概率密度函數。

沿用點估計法的基本思想[14-18]，對上式采用一維Gauss-Hermite數值積分，可靠度指標的均值即平均可靠指標可由式(9)表示：

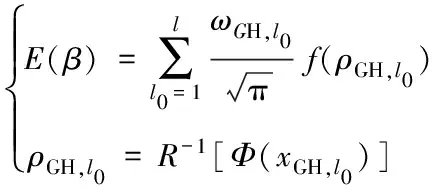
(9)

式中：ωGH，i是Gauss-Hermite積分的權系數；xGH，i是根據Gauss-Hermite積分的節點；Φ(．)表示標準正態分布的分布函數；R-1(．)表示Rosenblatt逆變換函數[19]；ρGH，i是根據xGH，i的Rosenblatt逆變換得到的對應荷載效應比的值；l為積分點總數，文中取l=7，Gauss-Hermite 7點積分的權系數與節點示于表5。

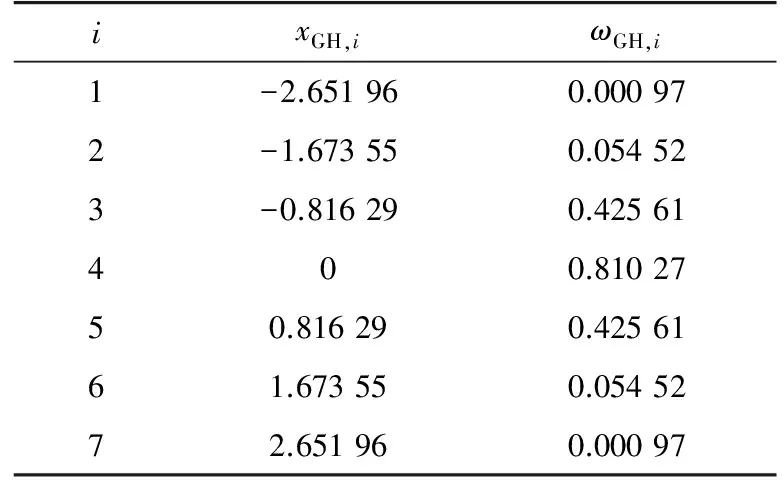
表5　Gauss-Hermite 7點積分的權系數與節點Tab.5　Abscissas and weights forGauss-Hermite quadrature with l=7

3　風荷載下輸電塔可靠度的校準

基于以上平均可靠指標的計算方法，分別討論在不同風速下(22 m/s，24 m/s，26 m/s，27 m/s，29 m/s，30 m/s，32 m/s，34 m/s，35m/s)，不同線條風占比(χ=0.2，0.3，0.4)和不同的結構重要性系數(γ0=1.0，1.1，1.2)對平均可靠指標的影響，可靠度校準結果如表6—11所示。

綜合上述，根據表6—11所示平均可靠度指標，可進一步求得當γ0=1時，可靠指標的均值為3.38；γ0=1.1時，可靠指標的均值為3.76；γ0=1.2時，可靠指標的均值為4.11；而基于此分布模型下采用規范規定的使用設計表達式計算可知，當γ0=1時，可靠指標的均值為2.77；γ0=1.1時，可靠指標的均值為3.28；γ0=1.2時，可靠指標的均值為3.75。

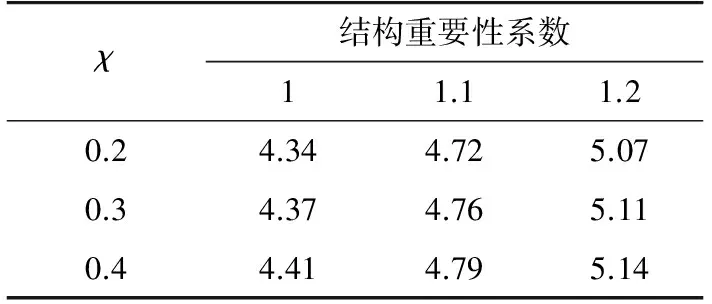
表6　風速22 m/s時平均可靠指標Tab.6　Mean value of β at v=22 m/s

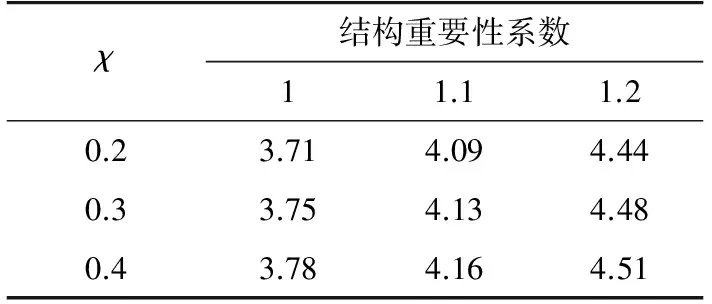
表7　風速24 m/s時平均可靠指標Tab.7　Mean value of β at v=24 m/s

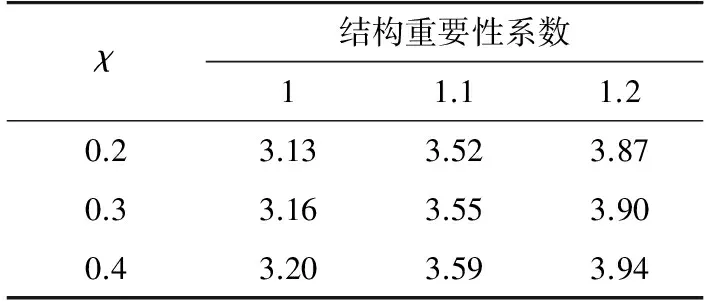
表8　風速26 m/s時平均可靠指標Tab.8　Mean value of β at v=26 m/s

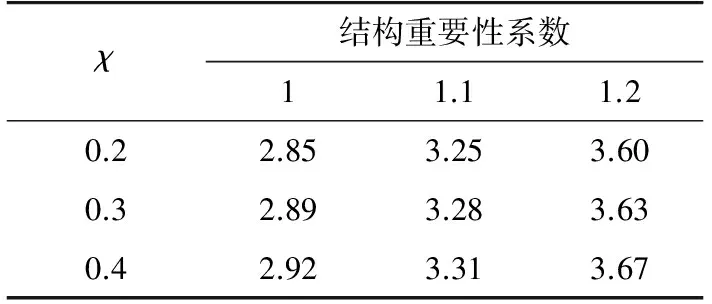
表9　風速27 m/s時平均可靠指標Tab.9　Mean value of β at v=27 m/s

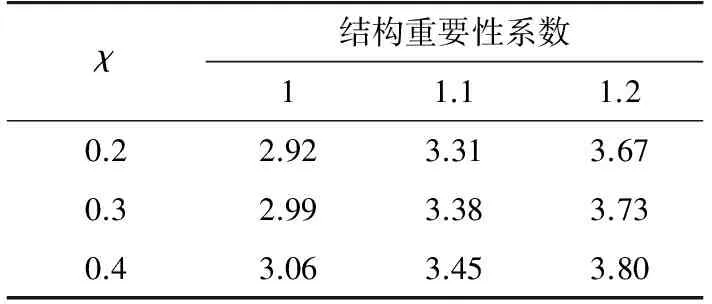
表10　風速30 m/s時平均可靠指標Tab.10　Mean value of β at v=30 m/s

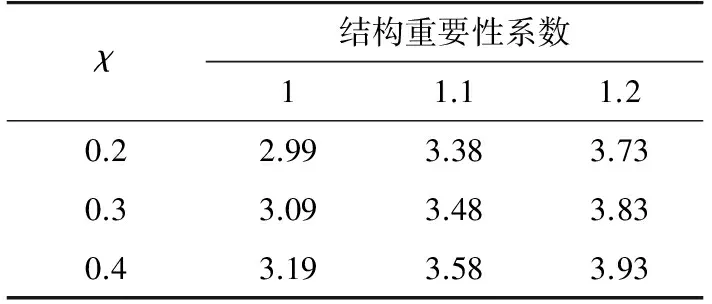
表11　風速35 m/s時可靠指標Tab.11　Mean value of β at v=35m/s

4　結語

基于荷載效應比的分布擬合，并結合點估計法的基本思想，文中提出了輸電塔桿塔結構構件平均可靠度指標的計算方法。與傳統方法相比，文中方法首次嘗試利用荷載效應比的分布校驗現有規范內蘊的平均可靠水準。為驗證方法的可行性，以輸電塔恒風組合的軸心受壓構件為研究對象，首先通過大量結構分析得到荷載效應比的樣本點，再通過分布擬合得到荷載效應比的分布。基于該分布，分別計算了不同風速下，不同線條風占比以及不同結構重要性系數下的輸電塔平均可靠指標。

參考文獻：

[1] GB/50068—2001 建筑結構可靠度設計統一標準[S].中國建筑工業出版社，2002.

GB/50068—2001 Unified standard for reliability design of building structures [S]. China Buolding Industry Press,2002.

[2] 蔣友寶，楊偉軍． 可變荷載效應占高比重時荷載分項系數取值研究[J]． 建筑結構學報，2012，33(12)：130-135.

JIANG Youbao，YANG Weijun．Research on values of load partial factors with large ratios of variable load effects[J]．Journal of Building Structures，2012，33(12)：130-135.

[3] 馮云芬，貢金鑫． 輸電線路桿塔構件可靠度校準[J]． 電力建設，2014，35(5)：13-20.

FENG Yunfen，GONG Jinxin． Reliability calibration of tower members in transmission line[J]． Electric Power Construction，2014，35(5)：13-20．

[4] 李峰，袁駿． 我國輸電線路鐵塔結構設計可靠度研究[J]． 電力建設，2010，31(11)：18-23.

LI Feng，YUAN Jun． Research on reliability of transmission tower structure design in china[J]． Electric Power Construction，2010，31(11)：18-23．

[5] 王松濤． 現行輸電塔設計規范可靠度水準的評估與分析[D]． 重慶大學，2014.

WANG Songtao． Reliability assessment and analysis of the current design code for transmission towers[D]． Chongqing University，2014.

[6] 劉靜波． 輸電塔結構設計表達式分項系數合理性及體系可靠度分析[D]． 重慶大學，2016.

LIU Jingbo． Rationality of partial coefficient in design expression and system reliability analysis of transmission tower[D]． Chongqing University，2016.

[7] 曹俊涵，郭曉波． 用MATLAB曲線擬合工具箱計算藥物溶出度Weibull分布參數[J]． 藥學進展，2006，30(12)：556-559.

CAO Junhan，GUO Xiaobo． Calculation of Weibull’s distribution parameters for drug dissolution by MATLAB curvefit toolbox[J]． Progress in Pharmaceutical Sciences，2006，30(12)：556-559．

[8] 肖鄭穎． 基于MATLAB的強度分布曲線的擬合研究[J]． 湖南農機，2012，39(7)：36-36.

XIAO Zhengyin． The curve fitting research of intensity profiles based on MATLAB[J]． Hunan Agricultural Machinery，2012，39(7)：36-36．

[9] BOTEV Z I，GROTOWSKI J F，KROESE D P． Kernel density estimation via diffusion[J]． Annals of Statistics，2010，38(5)：2916-2957.

[10] DL/T 5154—2012 架空輸電線路桿塔結構設計技術規定[S]. 中國計劃出版社，2012.

DL/T 5154—2012 Design of latticed steel transmission structures [S]. China Planning Press,2012.

[11] 趙國藩． 工程結構可靠度[M]． 北京：水利出版社，1984.

ZHAO Guofan． Reliability for engineering structures [M]． B￣e￣i￣jing：Hydraulic Press，1984.

[12] 李繼華． 建筑結構概率極限狀態設計[M]． 北京：中國建筑工業出版社，1990.

LI Jihua． Probabilistic limit state design of building structures[M]． Beijing：China Architecture & Building Press，1990.

[13] 趙國藩. 工程結構可靠性理論與應用[M]． 大連：大連理工大學出版社，1996.

ZHAO Guofan. Reliability theory and its applications to engineering structures[M]． Dalian：Dalian University of T￣e￣c￣h￣n￣o￣logy Press，1996.

[14] FAN W L． Adaptive estimation of statistical moments of the responses of random systems [J]． Probabilistic Engineering Mechanics，2016，43：50-67.

[15] 范文亮，李正良，韓楓． 單變量函數統計矩的點估計法性能比較[J]． 工程力學，2012，29(9)：1-10.

FAN Wenliang，LI Zhengliang，HAN Feng． Comparison of point estimate methods for probability moments of univariate function[J]. Engineering Mechanics,2012，29(9)：1-10．

[16] 范文亮，李正良，韓楓． 多變量函數統計矩點估計法的性能比較[J]． 工程力學，2012，29(11)：1-11.

FAN Wenliang，LI Zhengliang，HAN Feng． Comparison of point estimate methods for probability moments of multivariate function[J]． Engineering Mechanics． 2012，29(9)：1-10．

[17] RAHMAN S，XU H． A univariate dimension-reduction method for multi-dimensional integration in stochastic mechanics[J]． Probabilistic Engineering Mechanics，2004，19(4)：393-408.

[18] XU H，RAHMAN S． A generalized dimension-reduction method for multi-dimensional integration in stochastic mechanics (Int．J．Numer．Meth．Engng 2004, 61：1992-2019)[J]． I￣n￣t￣e￣r￣national Journal for Numerical Methods in Engineering，2006，65(13)：2292-2292.

[19] ROSENBLATT M． Remarks on a multivariate transformation [J]． The Annals of Mathematical Statistics，1952，23(3)：470-472．