基于特征選擇的K-means聚類異常檢測方法

◆樊 蓉 李 娜

?

基于特征選擇的K-means聚類異常檢測方法

◆樊 蓉 李 娜

（四川大學計算機學院 四川 610065）

K-means算法是一種采用距離作為相似性評價指標的聚類算法，其快速簡潔的特點在異常檢測場景中有一定的應用價值。但是，傳統的K-means聚類算法在選取初始中心和度量相似性上有一定缺陷。針對傳統的K-means算法中存在的問題，本文對原有的方法進行了改進。第一，在初始化聚類中心時選取了一種優化的方法作為初始聚類中心，替代原有的隨機選擇方法以減少計算量和迭代次數。第二，采用基于信息熵屬性加權的樣本相似性度量來進一步精確樣本差異。實驗過程中，針對異常檢測數據含有冗余特征，對樣本數據做了冗余特征過濾，實驗結果表明改進之后的方法較傳統的K-means算法有更好的檢測效果。

K-means算法；異常檢測；聚類；冗余特征

0 引言

異常檢測就是假設入侵行為異常于正常行為，如果當前行為與正常行為存在一定的偏差就認為系統受到攻擊[1]。這個特點使其有能力識別未知類型的攻擊，異常檢測是入侵檢測方面的一個研究熱點。從Wenke Lee[2]使用數據挖掘方法得到屬于不同數據的行為輪廓開始，聚類算法在異常檢測方面廣為使用。江頡[3]和Aljarah[4]針對K值選取提出的改進聚類算法，周涓等人[5]針對中心選取提出的一種多個聚類中心選擇算法等。K-means聚類算法在異常檢測方面有著廣泛的應用和良好的效果。但是存在幾個問題，一是K個中心初始位置的選取和確定，中心初始位置選擇不好會導致迭代次數增多和計算量增大，嚴重影響聚類效果；二是樣本度量問題，K-means算法采用各屬性無差異的歐式距離來計算樣本之間的相似性，沒有考慮不同屬性權重對樣本的影響使得相似性度量不準確；三是冗余屬性和噪音會對聚類結果產生偏離，計算時對效率影響較大。針對方法涉及的幾個問題，本文提出一種基于特征選擇的K-means聚類算法。首先，采用Fisher特征選擇對特征重要度排序，用順序前向最優搜索的方法快速確定所選特征數量由小到大的最優特征子集，所選的特征子集能最大程度的代表原始特征，并且去除不必要的特征和噪音。其次，采用一種優化的方法來選取初始聚類中心以減少計算量和迭代次數；最后，計算各屬性的信息熵作為屬性權重來度量樣本之間的差異，區別不同屬性對樣本的貢獻。本文提出的方法在異常檢測方面取得不錯的檢測效果。

1 一種改進的K-means聚類算法

1.1 K-means聚類算法

K-means算法是一種典型的基于距離度量相似性的聚類算法，算法的主要思想是差異最小最相似，根據樣本之間的相似程度劃分至相應的簇內[6]。具體流程如圖1所示：

圖1 K-means聚類流程

1.2信息熵屬性權重確定

信息熵是一種客觀權重確定方法，它是在原始數據的基礎上，表示信息有用程度大小的一種度量方式。具體流程如圖2所示:

圖2 信息熵屬性權重計算

1.3改進的K-means聚類算法

傳統的K-means聚類算法選擇聚類中心的方法為隨機選擇，導致聚類迭代次數增多和計算量增大，陷入局部最優以及樣本各屬性的平等對待影響聚類效果。為了消除這種影響，本文提出的方法在原有的方法上進行改進，一定程度消除了以上因素的影響。具體流程如圖3所示：

圖3 改進k-means聚類流程圖

2 基于特征選擇的K-means聚類異常檢測方法

2.1 Fisher特征選擇

Fisher特征選擇是一種基于距離度量的過濾式特征選擇算法。其基本思想為將不同類樣本間的距離最大化及將同類樣本間的距離最小化[7]。Fisher特征選擇算法流程如下圖4所示：

圖4 Fisher分特征排序

2.2基于特征選擇的K-means聚類異常檢測

首先對輸入樣本根據Fisher分進行特征選擇，采用前向序列搜索選出能夠代表樣本的最優特征子集，然后基于改進的K均值算法進行聚類，方法流程如圖5所示。

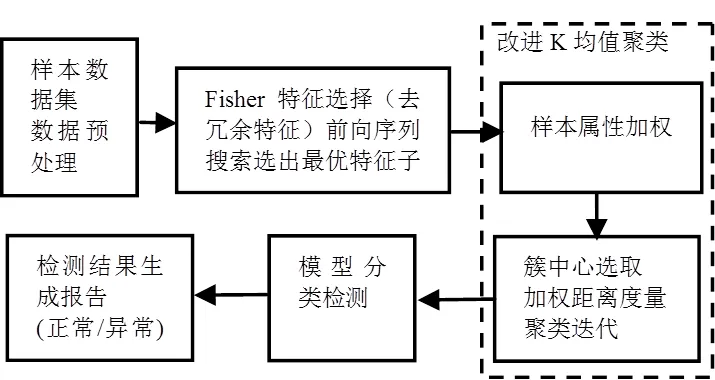
圖5 基于特征選擇的K-means聚類異常檢測流程

3 實驗測試與分析

3.1實驗數據與評價指標

實驗將選取10000條樣本記錄作為實驗數據集輸入，每一條樣本記錄由41維向量特征組成。在進行實驗之前，對樣本記錄做標準化和歸一化處理以消除樣本差異及覆蓋等影響。實驗效果則采用檢測率、誤報率、檢測時間為評價指標。其中，樣本集來自當前入侵檢測領域權威數據集KDD，實驗平臺為開放的數據挖掘平臺weka。

3.2實驗設計與結果分析

本文設置三組實驗：

第一組實驗的目的是證明本文的特征選擇所選出的特征對于聚類檢測具有可行性。實驗采用Fisher分對抽樣的41維數據進行排序的結果如表1所示：

表1 Fisher分對數據特征排序

為了得到最優的特征子集并且不丟失必要的特征，本文采用前向序列搜索依次加入5、3、2、1個特征進行聚類的結果如圖6所示：

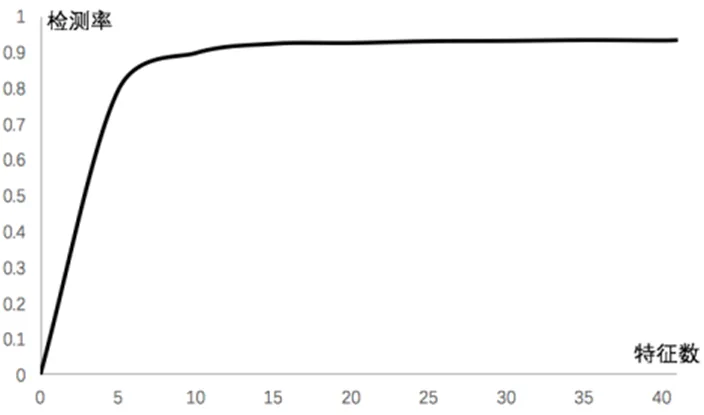
圖6 特征數與聚類檢測率結果

通過實驗，從圖中可以看出，首先加入前5個特征有較好的檢測率，然后逐次加入3、2、1個特征時檢測率有所提高，當所加入的特征數為11時，檢測率趨于穩定，通過前向序列搜索得出最優特征子集為{23 32 24 12 3 2 33 27 34 28 4}，相比于原始41維數據，得到的最優特征子集能很好的得到檢測效果，與原始的數據檢測率相當，有效的減少了計算資源。

第二組實驗設計了2000條數據樣本，分別采用本文改進的K-means聚類方法和傳統方法做聚類對比實驗，實驗檢測結果如圖7所示。

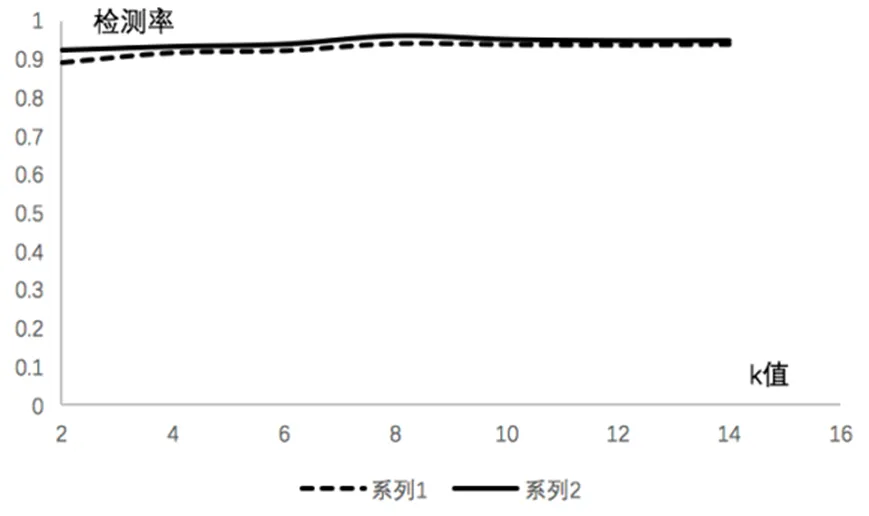
圖7 傳統K-means與改進K-means檢測率對比

圖7中序列1代表傳統的K-means算法，序列2代表改進的K-means算法。實驗數據分析可以得出在K取不同值情況下檢測結果也會隨之變化，當K取值為8時，兩種方法的檢測效果都達到最佳。由于改進的方法優化聚類中心的選取，采用信息熵加權的距離計算，使得檢測率高于傳統方法。

第三組實驗的目的在于驗證本文提出的方法能夠取得較好的檢測結果。設計兩組相同數據集，采用兩種方法做對比實驗，重復實驗10次，實驗取平均值。檢測結果如表2所示：

表2 傳統K-means與本文方法檢測結果對比

通過本組對比實驗可以看到本文改進的方法在檢測的誤報率相當的情況下，在檢測率上有一定的提高，在檢測時間上也有著顯著的縮減。由于采用特征選擇去除不必要特征使得數據維數縮減，減少了聚類時間，去除的噪音數據也消除了對樣本相似性度量的影響。同時，優化的聚類中心選取與加權的距離度量也使得檢測的檢確率有一定的提升。

4 結束語

本文通過Fisher進行特征選擇過濾了冗余特征，大大縮減了檢測時間，提高檢測效率，同時采用改進的K-means算法進行聚類檢測提高了檢測率。經實驗驗證可以得到，本文提出的改進的K-means聚類異常檢測方法相較于傳統的方法有著較好的檢測效果。

[1]卿斯漢, 蔣建春, 馬恒太等.入侵檢測技術研究綜述[J]. 通信學報，2004 .

[2]Lee W, Stolfo S J.A framework for constructing features and models for intrusion detection systems[J].ACM Transactions on Information and System Security(TISSEC)，2000.

[3]江頡, 王卓方, 陳鐵明等.自適應AP聚類算法及其在入侵檢測中的應用[J].通信學報, 2015.

[4]Aljarah I，Ludwig S A．Parallel particle swarm optimization clustering algorithm based on MapＲeduce methodology［C］/ /Proc of the 4th World Congress on Nature and Biologically Inspired Computing. [S.l.]: IEEE Press，2012.

[5]周涓, 熊忠陽, 張玉芳等.基于最大最小距離法的多中心聚類算法[J].計算機應用, 2006.

[6]李銳，李鵬，曲亞東，王斌譯.Peter HARRINGTON.機器學習實戰[M].北京:人民郵電出版社, 2013.

[7] 程正東，章毓晉，樊祥等.常用Fisher判別函數的判別矩陣研究[J].自動化學報，2010.

[8]CHENG Zhengdong，ZHANG Yujin，FAN Xiang，et al.Study on Discriminant Matrices of Commonly-Used Fisher Discriminant Functions [J]. SctaAutomaticaSinica，2010.

國家重點研發計劃(2016yfb0800604，2016yfb0800605)，國家自然科學基金項目(61572334)。