基于SESAM的遠洋秋刀魚船波浪載荷預報

楊子恒，謝永和

(浙江海洋大學船舶與機電工程學院，浙江舟山 316022)

船舶是在波浪環境中作業營運的，對作用在船體上波浪載荷的計算是評估整船強度安全的前提，也是設計耐波性良好船舶的基礎[1]。目前，對于大中型船舶波浪載荷的計算，可采用CCS的相關規范[2]對波浪彎矩和剪力等參數進行公式計算，但是對中小型船舶尤其是中小型的遠洋漁船波浪載荷的計算還未有相應的規范計算。而目前，利用有限元軟件對整船的結構強度進行分析與評估已較為成熟，國內已有不少學者通過各類方法預報船型的波浪載荷，并通過設計波法確定船型受到的波浪載荷，進而利用通用有限元軟件對船型的整體強度進行研究和分析[3-7]，但是對于漁船這類特殊船型直接計算和研究還較為少見。因此，有必要對中小型遠洋漁船的波浪載荷長期預報進行計算與研究，為中小型遠洋漁船船型的結構強度計算提供參考。

本文以53 m遠洋秋刀魚船為研究對象，利用SESAM軟件[8-9]并選擇航行作業區域的西北太平洋波浪譜對其進行了波浪載荷水平彎矩和垂直彎矩兩個控制參數的長期預報，分析了不同裝載情況、浪向角等對預報值的影響。

1 目標船型和水動力計算模型

本船為鋼質、單層甲板、雙層底、單機、單槳、艉機型船型，主要在西北太平洋海區從事秋刀魚捕撈作業，其主要參數見表1。

表1 船型主要參數表Tab.1 The main dimensions and parameters of ship

采用SESAM的GeniE模塊建立目標船型的水動力模型，X方向指向船首，Y方向指向船體左舷，Z方向垂直向上，坐標原點位于艉垂線和基線的交點，肋骨間距0.50 m，如圖1所示。

圖1 濕表面模型Fig.1 Panel model

圖2 質量模型Fig.2 Mass model

同時通過對船型內各種重量的模擬建立質量模型，并對照實船裝載計算書和實際船舶的重量分布資料調整模型的重心和重量，使整船模型質量與船舶靜水浮態相匹配，如圖2所示。

2 載荷預報的參數選擇

2.1 計算剖面的選擇

本文主要研究漁船船體縱向方向上橫截面處的彎矩等船體端面外載荷，選取了24個橫截面，選取剖面的位置如圖3所示。

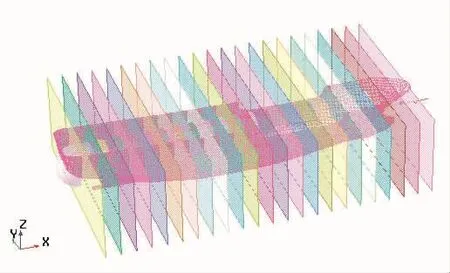
圖3 橫截面位置Fig.3 The locations of load cross sections

2.2 波浪散布圖的選擇

在波浪載荷的預報中，我們通常根據目標船型的實際作業海域來選擇合適的波浪統計資料來作為船型運動響應的海浪環境參數。本文波浪載荷預報海況采用西北太平洋海域中海況最嚴重的海區NW15(160°-170°E，35°-60°N)的海浪長期統計分布資料[10]。

2.3 波浪參數的選擇

2.3.1 浪向角的選擇

在計算波浪載荷響應過程中，在0°～180°的范圍內選取13個浪向角，其間隔為15°，每個浪向均有0.076 92的概率作用在船體上。

2.3.2 計算頻率的選取

按照波長與船長比0.2～2.0的范圍內選取，步長取0.05，共37個。波長則通過式(1)進行計算。

3 結果分析

根據目標船型的裝載計算書及文獻[11]，本文選取了豐收返港、捕魚中、空載到港3個典型裝載工況來分析研究秋刀魚船的波浪載荷響應。

3.1 波浪載荷沿船長分布

圖4和圖5為利用西北太平洋NW15的波浪散布圖進行波浪載荷預報后，波浪彎矩沿船長方向的分布情況。

圖4 垂向波浪彎矩沿船長分布Fig.4 The distribution of VWBM along ship length

圖5 水平波浪彎矩沿船長分布Fig.5 The distribution of HWBM along ship length

從圖4可以看出，空載到港、捕魚中、豐收返港工況的垂向波浪彎矩變化由艉至艏均呈現減小后增大再減小的趨勢，在距尾垂線3 m左右出現了1個極小值。而最大值均出現在船中偏尾的位置，豐收返港工況的垂向波浪彎矩普遍比空載到港工況大，而捕魚中工況的數值則基本位于兩者之間。

而在水平彎矩的分布上(圖5)，3工況彎矩的最大值所在的位置依次向艉部偏移。在船尾至0.20L范圍內，捕魚中工況的水平彎矩普遍高于空載到港而低于豐收返港工況；在其它船長范圍內，空載到港的水平彎矩均大于另2種工況，而豐收返港的彎矩則最小。

3.2 主要載荷參數長期預報值

圖6和圖7給出了秋刀魚船在豐收返港、捕魚中、空載到港3個工況下某截面上水平彎矩和垂向彎矩2個主要載荷控制參數不同重現期的預報極值和超越概率水平10-8下的預報極值。

圖6 水平波浪彎矩長期預報值Fig.6 Long term prediction value of HWBM

圖7 垂直波浪彎矩長期預報值Fig.7 Long term prediction value of VWBM

由圖5及圖6對比，在同一重現期或超越概率下豐收返港的垂向波浪彎矩的預報極值均大于空載到港，而其水平彎矩的預報極值則均小于空載到港的預報極值，而捕魚中工況的預報極值則位于兩者之間。同時，計算得到的超越概率10-8下的水平彎矩的預報極值均大于重現期10 a的預報極值且接近重現期20 a的預報極值，部分極值甚至大于重現期50 a的預報極值。

3.3 浪向角及截面位置對波浪載荷的影響

圖8和圖9為目標船型在豐收返港和空載到港工況下的各主要載荷控制參數在重現期100 a下的的長期預報極值在不同浪向角上的分布。

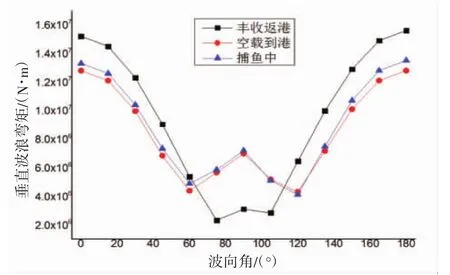
圖8 垂直波浪彎矩在不同浪向的分布Fig.8 Vertical bending moment of in different wave directions

圖9 水平波浪彎矩在不同浪向的分布Fig.9 Horizontal bending moment in different wave directions

從圖8可以看出：3種工況垂直彎矩的預報極值均出現在浪向角為0°或180°時，即目標船型在迎浪或順浪航行時垂直彎矩最大，同時隨浪向趨近橫浪時呈現先減小后增大的趨勢，在橫浪時達到小波峰。在此截面上，豐收返港的垂直波浪彎矩在大部分的浪向上均大于空載到港，但在65°至110°左右時小于空載到港。而捕魚中工況基本處于兩者之間，但在浪向65°至90°左右時大于另2種工況。船型在此截面上各工況的垂直彎矩的極大值均出現在浪向角為180°的時候，即順浪航行時。

而在水平彎矩上(圖9)，隨著浪向趨于橫浪，3種工況的水平彎矩逐漸增大，且空載到港的水平彎矩在各個浪向角上均大于豐收返港，而捕魚中工況的水平彎矩則大于豐收返港小于空載到港。在此截面上，各工況水平彎矩的最大值均出現在浪向角為90°即橫浪航行的狀態下。

3.4 橫傾作業工況的波浪載荷預報

由于秋刀魚船舷外抄網到船中網囊卸魚是一個動態變化的過程，這一過程會導致船體一定時間內不同橫傾情況的產生。同時，網具伸出舷外的重量以及起吊魚獲物網囊的重量變化難以估算，起網時船型的橫傾角也難以計算。因此，本小節以捕魚中工況的裝載條件為基礎，假定橫傾5°和10°2個橫傾角來簡單模擬舷側起網時船型的橫傾狀態，并通過在質量模型中加載船型外的質量點來實現模型的橫傾，分析橫傾角對波浪載荷預報的影響。

計算中各類參數的選取與上文保持一致，得到的各截面水平彎矩和垂向彎矩如圖10和圖11所示。

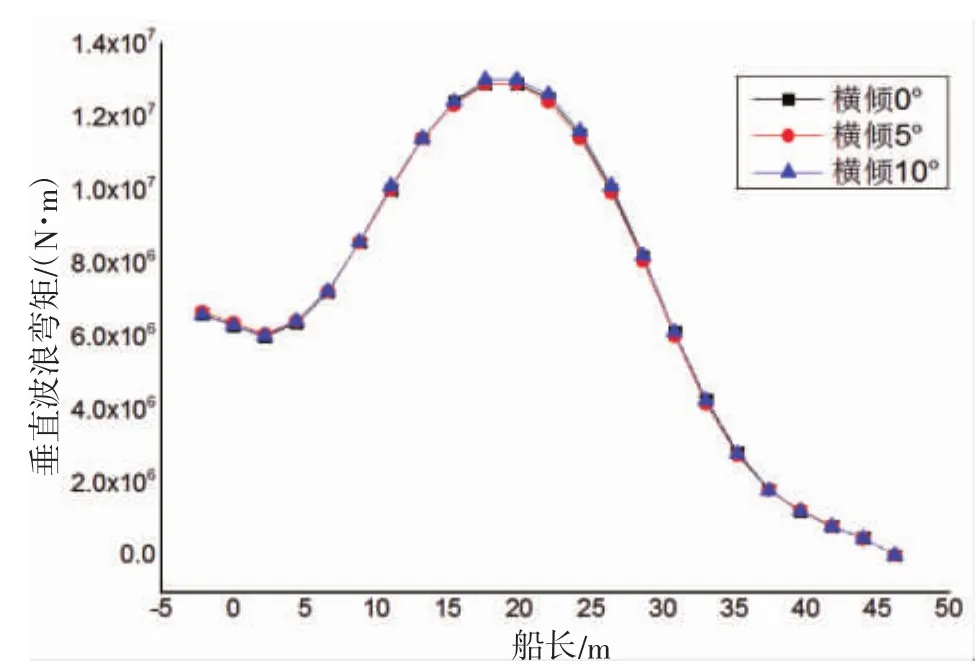
圖10 垂向波浪彎矩沿船長分布Fig.10 The distribution of VWBM along ship length

圖11 水平波浪彎矩沿船長分布Fig.11 The distribution of HWBM along ship length

從圖10可以看出：3種狀態下，垂向波浪彎矩沿船長方向的分布趨勢保持一致，船型橫傾角的變化對垂向彎矩無較大的影響，三者垂向彎矩的最大值均在船中區域。而在船中范圍內橫傾角10°的垂直彎矩略大于橫傾角5°狀態，而此處無橫傾狀態的彎矩最小。

在水平波浪彎矩方面(圖11)，三種狀態都呈現先增大后減小的趨勢，且最大值位于船中靠艉的區域內。在船尾區域內，無橫傾狀態的水平彎矩大于橫傾狀態的彎矩；在船中偏艉區域，隨著橫傾角的增大，水平波浪彎矩也逐漸增大；而在船首范圍內，橫傾角的變化對水平彎矩無明顯的影響。

4 小結

本文基于西北太平洋海域海區NW15的波浪統計資料的環境參數，利用DNV SESAM軟件對秋刀魚船的典型工況進行了水平和垂直彎矩2個控制參數下波浪載荷的長期預報，得到了不同重現期和概率水平10-8下的預報極值，同時研究了不同浪向角對船型波浪載荷和船體運動預報的影響。此外，本文還通過假定橫傾角的方法來模擬舷側抄網時船型橫傾的狀態，分析了船型不同橫傾角對波浪載荷預報的影響。本文的研究能夠為中小型遠洋漁船的波浪載荷計算尤其是考慮漁船作業情況下波浪載荷的預報提供一定的參考，同時也為下一步進行船型結構強度直接計算與疲勞分析打下基礎。