基于密度感知模式的生物序列分類算法

胡耀煒，段　磊,2，李　嶺，韓　超

(1.四川大學 計算機學院，成都 610065；　2.四川大學 華西公共衛(wèi)生學院，成都 610041；3.四川大學 生命科學學院，成都 610041)(*通信作者電子郵箱leiduan@scu.edu.cn)

0　引言

理解細胞的分子生物機制的一個關鍵因素是通過對生物序列進行分類來了解不同生物序列的意義和功能[1-2]。隨著分子生物學技術的快速發(fā)展，產生了大量的生物序列數據，如DNA序列、蛋白質序列等[3]。相比普通的符號序列數據，生物序列數據具有以下明顯特點：1)組成生物序列中的符號總數少。例如，一條DNA序列由4種堿基({a，c，g，t})組成，一條蛋白質序列由20種氨基酸組成。在相同長度下，生物序列包含更多的重復出現的符號。2)生物序列的長度較長，例如一條基因或蛋白序列的長度通常在104的級別。3)不同類別的生物序列樣本規(guī)模不平衡。受限于數據來源和數據采集成本，不同類別的生物序列在樣本的長度、數量等統(tǒng)計指標上差別明顯。

目前生物序列分類的方法大致可以分為三類：1)利用序列對比工具如FASTA(FAST All)[4]、BLAST(Basic Local Alignment Search Tool)[5]進行序列對比, 找出已知類標的數據庫中最為相似的序列；2)基于統(tǒng)計或機器學習的方法，通過一些統(tǒng)計方法抽取序列特征，然后利用機器學習的方法進行序列分類[6-9]；3)利用不同的模式挖掘來提取特征并進行分類[10-11]。利用序列對比工具進行分類在數據量較大時需要巨大的計算量；統(tǒng)計或機器學習方法所得到的結果盡管較好但解釋性較差；而基于模式的方法具有較強的解釋性，但存在分類效果不夠理想、運行時間較長的問題。

本文針對基于模式的分類方法，設計了具有可解釋性的基于密度感知模式的生物序列分類(Biological Sequence Classifier based on density-aware patterns, BSC)算法，其主要工作包括：1)引入了“密度感知”來評價模式在單條序列中出現的頻繁度，并提出了密度感知模型的概念；2)使用“間隔約束”來提高模式匹配的效率；3)在真實的蛋白質序列和基因序列數據上進行翔實的實驗，驗證了BSC算法有較高的生物序列分類精度和執(zhí)行效率。

1　問題定義

本文將允許在序列中出現的符號的集合稱為符號集，記作Σ。例如，對于DNA序列，Σ={a，c，g，t}。序列由符號集中的元素按序組成，表示為S=e1e2…en(ei∈Σ，1≤i≤n)。用S[i]表示序列S中第i個元素，|S|表示序列S的長度，即S中元素的總數。例如，給定基因序列S=acgcac，S[3]=g， |S|=6。

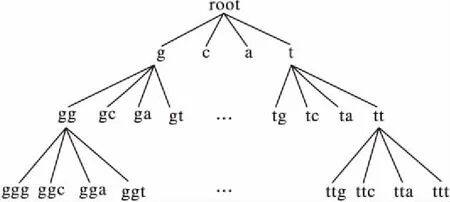
序列S中元素S[i]和S[j](1≤i

給定序列S和序列P，若P=S[k1]S[k2]…S[km]，其中1≤k1

若存在實例〈k1,k2,…,km〉∈ins(P,S)滿足? 1≤i≤m，γ.min≤gap(S，ki，ki+1)≤γ.max，那么稱實例〈k1,k2, …,km〉滿足間隔約束γ，且P是S的γ-子序列(或稱Pγ-匹配S)，記作P?S。例如：給定序列S=acgcact，序列P=agc，間隔約束γ=[0, 1]，則P在S中的實例有〈1，3，4〉。由于gap(S， 1，3)=1∈γ且gap(S，3，4)=0∈γ，因此P?S。將ins(P，S)中滿足間隔約束γ的實例的集合記為γ-ins(P,S)。容易看出，γ-ins(P，S)?ins(P，S)。

給定序列S，間隔約束γ和模式長度l，則序列的長度為l且滿足間隔約束γ的實例的數量N為|{〈k1,k2, …,kl〉|? 1≤i≤l(1≤ki≤|S|)(? 1≤j

定義1密度。給定序列P和S，間隔約束γ，序列P在S的密度den(P，S)為：

den(P,S)=|γ-ins(P,S)|/N

(1)

若P?S，即γ-ins(P,S)≠?,那么，1/N≤den(P,S)≤1.0。

定義2支持度。給定序列集合D、間隔約束γ和密度閾值δ，序列P的支持度記作sup(P，δ，D)，為Pγ-匹配D中序列，且匹配密度不小于δ的序列的個數與D中序列樣本總數的比值，即:

sup(P,δ,D)=|{S∈D|den(P,S)≥δ}|/|D|

(2)

給定支持度閾值，若sup(P，δ，D)≥α，那么稱P為密度感知模式。

給定類標簽集合C(|C|個類別)，序列數據集(Sequential DataBase, SDB)為由一個序列數據對象及其對應的唯一類標簽組成的二元組的集合，記作SDB={〈S,c〉}，其中S是一條序列，c∈C是S的類標簽。為便于描述，將所有類別為c的序列組成的集合記為Dc，即Dc={S|〈S,c〉∈SDB}。那么，給定類標簽Ci，Cj∈C，Dci∩Dcj=?。

定義3置信度。給定序列數據集SDB，間隔約束γ，密度閾值δ。序列P關于類別c的置信度(記作conf(P，c))為:

(3)

根據統(tǒng)計學習的思想，某個序列的重要性隨著它在該類中出現的次數呈正比增加，同時隨著它在其他類中出現的頻率呈反比下降。即序列P出現在類別c中頻率很高，同時又出現在較少的類中，則P和c類有較大的相關性，可作為用于分類的模式。根據該思想具有以下對比度定義：

定義4對比度。給定序列數據集SDB，間隔約束γ，密度閾值δ,序列P關于類別c的對比度(記作cst(P，c))為:

cst(P,c)=sup(P,δ,Dc)×(1+lg(|C|/m))

(4)

其中，m=|{i∈C|sup(P，δ，Di)≥α}|。

表1列出了本文常用的符號及其定義。

表1　符號及定義Tab. 1　Notations and definitions

2　BSC算法設計

為了對生物序列數據集分類，本文提出了一種基于密度感知模式的生物序列分類算法BSC。BSC算法主要步驟包括：1)密度感知模式挖掘；2)生成分類規(guī)則；3)構建序列分類器。

2.1　密度感知模式挖掘

集合枚舉樹(圖1)是廣泛采用的生成頻繁模式的算法，BSC算法采用遍歷集合枚舉樹的方式生成候選模式。

圖1　DNA集合枚舉樹Fig. 1　Enumeration tree of DNA set

為了獲得較高的執(zhí)行效率，可根據模式生成算法的性質得到剪枝策略。

引理1給定序列集合D，間隔約束γ，密度閾值δ，支持度閾值α，序列P和P′(P′是P的連續(xù)子序列)，則sup(P′，δ，D)≥sup(P，δ，D)。

定理1給定序列集合D，間隔約束γ，支持度閾值α，序列P和P′(P′是P的連續(xù)子序列)，若sup(P′，0，D)<α,則sup(P，δ，D)<α。

證明因為sup(P′，0，D)<α，sup(P′，0，D)≥sup(P，0，D),又因為sup(P，0，D)≥sup(P，δ，D),所以sup(P，δ，D)<α。

證畢。

由定理1可以得到剪枝策略1。

剪枝策略1給定序列集合D，支持度閾值α和序列P，若sup(P，0，D)<α，則剪去集合枚舉樹中P和P的所有子節(jié)點。

本文采用基于廣度優(yōu)先遍歷集合枚舉樹生成候選模式的算法，基本思想為通過拼接兩個長度為l的候選模式生成長度為l+1的候選模式[13]。具體地，給定模式P和Q(|P|=|Q|=l)， 令pre(P)=P[1]P[2]…P[l-1]，suf(Q)=Q[2]Q[3]…Q[l]。 若pre(P)=suf(Q)，則可由模式P和Q生成長度為l+1的候選模式P⊕Q=Q[1]P[1]P[2]…P[l]=Q[1]Q[2]…Q[l]P[l]。算法1中給出了BSC算法生成密度感知模式的偽代碼。

算法1GENPATTERNS(D，α，δ)。

輸入數據集D，支持度閾值α，密度閾值δ;

輸出密度感知模式集合F。

Yl←Σ；F←{長度為1的密度感知模式}

whileYl≠? do

Yl+1←?

Yl←Yl{P∈Yl|sup(P，0，D)<α}

forP∈Yl，Q∈Yldo

ifpre(P)=suf(Q) then

Z=P⊕Q

Yl+1←Yl+1∪{Z}

ifsup(Z，δ，D)≥αthen

F←F∪{Z}

endif

endif

endfor

Yl←Yl+1

endwhile

returnF

2.2　生成規(guī)則

根據算法1可以從數據集SDB的每個類中挖掘到密度感知模式。若在序列集合Dc中挖掘出頻繁模式P，則生成的候選分類規(guī)則r形如：P?c。

數據集中每個類通常會生成大量候選分類規(guī)則，若直接應用所有候選規(guī)則進行分類不僅會增加計算開銷，還將引入低質量的規(guī)則導致分類效果不佳。因此，需要對候選分類規(guī)則進行評價以便挑選出分類能力強的規(guī)則。

置信度反映的是分類規(guī)則的確定性。給定分類規(guī)則r：P?c，置信度閾值β，如果conf(P，c)≥β，則密度感知模式P對c類具有較強分類能力。

對比度反映的是分類規(guī)則中密度感知模式P在c類中的重要程度。即c中P出現的頻率較高且出現在很少的類時，則P是一個能較好代表c的特征。

文獻[14]通過實驗驗證了當其他條件相同時，模式長度是評價模式分類能力的重要指標。

基于上述分析, 給出以下分類能力評價規(guī)則：

給定兩個分類規(guī)則r1：P?c，r2：P′ ?c。

1)如果conf(P，c)≥conf(P′，c)，那么r1?r2(r1優(yōu)于r2)。

2)如果conf(P，c)=conf(P′，c)且cst(P，c)≥cst(P′，c), 那么r1?r2。

3)如果conf(P，c)=conf(P′，c)，cst(P，c)=cst(P′，c)且|P|≥|P′|，那么r1?r2。

4)如果conf(P，c)=conf(P′，c)，cst(P，c)=cst(P′，c)，|P|=|P′|且P先于P′生成，那么r1?r2。

通過評價規(guī)則可以對候選分類規(guī)則進行排序。按分類能力的高低順序排好序的分類規(guī)則更加利于剪枝并挑選出分類能力較強的規(guī)則來構建分類器。

本文候選分類規(guī)則剪枝采用數據集覆蓋方法[15]，即從排好序的候選分類規(guī)則集合中依次取規(guī)則r對數據集D中的序列進行匹配，若數據集D中至少存在一條序列S滿足den(P，S)≥δ，則把此規(guī)則加入分類規(guī)則集合R中，并把序列S從數據集D中去除。該過程直到數據集D為空或沒有滿足匹配條件的序列為止。

當數據集SDB的每個類按上述方法進行匹配后，剩余序列最多的類的類標即為默認類標，默認類標在2.3節(jié)中用到。

算法2給出了生成分類規(guī)則的偽代碼。

算法2GENRULES(D，F，δ)。

輸入數據集D，密度感知模式集合F，密度閾值δ;

輸出分類規(guī)則集合R。

R←{P?c|P∈F}

/*構造分類規(guī)則,c為數據集D的類標*/

R←?

/*初始化分類規(guī)則集合R*/

sortR

/*按照分類能力評價規(guī)則進行排序*/

forr∈Rdo

forS∈Ddo

ifden(P，S)≥δthen

D←DS;

endif

endfor

R←R∪{r}

endfor

returnR

2.3　構建序列分類器

本節(jié)將根據算法2得到的分類規(guī)則集合來構建序列分類器，對未知序列進行分類。

在已經取得分類規(guī)則集合的情況下,若用分類規(guī)則去匹配待分類序列S，則會出現多個分類規(guī)則同時匹配S且這些規(guī)則屬于不同類別的情況，因此需要一種合適的判定方法來判定S屬于的類別。

容易想到用投票的方式來進行分類，匹配的規(guī)則中某個類的數量最多則預測待分類序列S屬于該類。然而，這種方式沒有考慮不同分類規(guī)則具有不同的可信度，因此分類效果不佳。本文則采用如下方式進行判定：

給定待分類序列S，分類規(guī)則集合Rs，則類別c在待分類序列S上的得分為：

(5)

若某條分類規(guī)則能夠匹配到待分類序列，則該規(guī)則的置信度作為它的得分累加到該規(guī)則預測的類別上。最終，得分最高的類為待分類序列所屬的類。算法3給出了構建序列分類器的偽代碼。

算法3CLASSIFIER(Rs，S，γ，k)。

輸入分類規(guī)則集合Rs，待分類序列S，間隔約束γ，k個分類規(guī)則;

輸出待分類序列S的類標。

對每個類c初始化score(c)為0

count←0

forr∈Rsandcount

ifγ-ins(P，S)≠? then

score(c)←score(c)+conf(P，c)

count←count+1

endif

endfor

ifcount=0 then

return 默認類標

returnscore(c)最大的類標

3　實驗與分析

3.1　實驗數據及環(huán)境

為驗證算法的有效性、執(zhí)行效率和不同參數對算法的影響，在4組真實的蛋白質序列數據集和基因序列數據集上進行實驗，包括：Thermophilic數據集[16]、Apoliporotein數據集[17]，以及來自于Pfam數據庫(http://pfam.xfam.org/)的Protein數據集和Gene數據集。這4組數據特征如表2所示。

為驗證BSC算法分類效果，與四種基于模式的可解釋性分類算法進行比較。其中：SCIS_HAR、SCIS_MA序列分類算法的代碼來自文獻[10]；另兩種算法則采用不同長度的頻繁模式作為特征，然后使用解釋性較強的決策樹和樸素貝葉斯作為分類算法進行分類，且算法由懷卡托智能分析環(huán)境(Waikato Environment for Knowledge Analysis, Weka)[18]實現，為便于敘述稱這兩種算法為DTree和NBayes。

五種算法均采用Java語言編寫，代碼公開在https://github.com/huyaowei1992/BSC。所有實驗都進行了10折交叉驗證，即把數據集分成10等份，每次取其中1份作為測試集，其他部分作為訓練集，依次進行10次實驗，求平均值作為最后結果。實驗在配置為Intel Core i7- 4760 3.60 GHz CPU，16 GB內存，Windows 7(64位)操作系統(tǒng)的個人計算機上完成。

表2　實驗數據集特征Tab. 2　Characteristics of experimental datasets

3.2　有效性實驗

為保證實驗的一致性，設定所有算法中相同的參數為：支持度閾值α=0.05，置信度閾值β=0.5，使用的分類規(guī)則數k=10。因對比的算法需要用戶設定生成模式的最大長度L，為了實驗的公平，BSC算法也添加該參數進行比較。

表3列出了五種算法在4組數據集中隨著模式最大長度L變化的分類精度情況，其中N/A表示算法因為內存溢出而無法完成實驗。由表3可以看出, BSC算法在4組數據集上都達到了最好的分類精度，同時L較小時BSC算法已經穩(wěn)定。SCIS_MA算法和SCIS_HAR算法分類精度隨L的增大而提高，但是這兩種算法對不同數據集分類效果差別較大。需要注意的是，對比算法在Gene數據的分類精度普遍不高的原因是：Gene數據的字符集比蛋白質更小，只有4個，因此模式的長度較小時，很容易在各類序列中得到匹配，因此需要枚舉出比蛋白質更長的模式，分類效果才會有所提升。但是增大模式長度時，需要枚舉的模式數量會指數增大，內存需求則會更多，所以根據實驗情況，本文列舉的模式的最大長度為7。

表3　算法分類準確率比較　%Tab. 3　Comparison of classification accuracy　%

BSC算法采用基于密度的頻繁模式，在長度不同的序列中，密度公式的分子分母都會根據長度的增大而增大，因此會削弱因為序列長度的差別對分類效果產生的影響；且支持度的公式同樣采用分數形式，對不同的數據規(guī)模有一定的歸一化的效果。

實驗結果表明，與其他基于模式的分類算法相比，BSC算法對蛋白質數據和基因數據有較高的分類精度，而且在模式長度較小時就可以達到較高精度，算法的有效性因此得到驗證。

3.3　執(zhí)行效率驗證

為驗證BSC算法的執(zhí)行效率，圖2記錄了有效性實驗中算法在4組數據集上隨L變化的運行時間。因為SCIS_HAR和SCIS_MA這兩個算法挖掘的模式和分類規(guī)則都完全一樣，只在構造分類器的過程中有所不同，所以運行時間幾乎相同。因此，圖2中使用SCIS統(tǒng)一表示。由圖2可以看出，算法的運行時間隨著L增大而變長，但BSC算法運行時間的增長幅度明顯小于其他算法。這是因為BSC算法在間隔約束的控制下生成的密度感知模式很少，因此算法的計算開銷較小。需要注意的是，BSC算法在L較小時，大部分模式被剪枝策略剪枝，不會再枚舉出更長模式，所以運行時間趨于穩(wěn)定。在圖中還可以觀察到，其他算法在L較大(L>2)時，運行時間會陡增，這是因為候選模式的規(guī)模隨L增大呈指數增長。實驗結果表明，對生物序列進行分類，BSC算法相對于其他分類算法具有更高的執(zhí)行效率。

圖2　不同模式長度的運行時間Fig.2　Runtime results for different pattern lengths

3.4　不同參數對算法的影響

為了探究不同的參數設置對BSC算法分類精度的影響，本文在4組數據集上進行了關于間隔約束γ和密度閾值δ不同取值時對分類精度影響的實驗。設定在蛋白質數據集中L=3，Gene數據集中L=7，其他參數同有效性實驗。當某一參數變化時，其他參數保持不變。

圖3展示了BSC算法中間隔約束γ變化對分類精度的影響。從3(a)看出，當γ的起始位置變化而間隔大小不變時，對分類精度的影響較小，但整體呈下降的趨勢。容易理解，相鄰的元素越接近，其間的聯系可能越強。如3(b)所示，在γ起始位置不變，間隔變大時，分類精度在蛋白質數據上變化較小，而在Gene數據上變化較大。這是因為在Gene數據集中找到的分類規(guī)則比在蛋白質數據集中挖掘的分類規(guī)則少。當γ變大時，更多的分類規(guī)則將由于不滿足密度閾值而被剪枝，最終將大幅影響分類的精度。

圖3　不同間隔約束的準確率Fig. 3　Accuracy results for different gap constraints

圖4展示了BSC算法中密度閾值δ變化對分類精度的影響。從圖4中可見, 當密度閾值設置過大時，兩組數據準確率急劇下降，因為密度閾值過大會有大量候選模式被剪枝，最后生成的分類規(guī)則過少導致分類精度下降。

3.5　參數設置討論

通過之前的實驗可以看出不同參數對實驗結果的影響，本節(jié)主要討論如何對參數進行設置。

對于支持度閾值α和置信度閾值β，本文推薦通常情況下設置α=0.05，這個值相對比較小，能夠選出足夠的模式；β=0.5是一個比較好的選擇，可以選擇出全部有分類能力的規(guī)則作為后面的備選。

從實驗可見，間隔約束γ的初始位置和間隔的設置在數值較小時會有微小的上下波動，但是隨著兩者數值的增大會呈現下降的趨勢；而隨著間隔區(qū)間的增大，算法的復雜度會不斷提升，因此本文推薦間隔約束γ的設置可以在數值較小的范圍內使用網格搜索，找到對于不同數據集的最優(yōu)參數設置。

密度閾值δ的設置同樣重要，δ的值太大或者太小都對結果有較大影響。本文推薦可以從δ=0.1開始，每次縮小到原來的1/10進行實驗，選擇最好的設置。

圖4　不同密度閾值的準確率Fig. 4　Accuracy results for different density thresholds

4　結語

生物序列分類是生命科學領域中的一項重要基礎問題。現有的易于解釋的基于模式的分類算法對生物序列分類存在分類精度不理想、模型訓練時間長的問題。針對這些問題，本文考慮了蛋白質序列和基因序列為代表的生物序列字符集規(guī)模小、序列長度較長的特點，設計了基于密度感知模式的生物序列分類算法。在算法中引入了密度的概念，用來挖掘密度較高的頻繁模式即密度感知模式，同時采用間隔約束的方式來減少訓練分類模型的時間。在4組真實的生物數據集上，將BSC算法與四種序列分類算法進行比較，結果顯示BSC算法在分類精度和運行效率上具有更好的表現，同時展示了不同的參數設置對于算法分類準確率的影響并簡要分析了原因。

在未來的工作中，將繼續(xù)改進BSC算法，針對目前的算法需要設置較多參數的問題作出改進。同時，將來可以借鑒目前統(tǒng)計方法，結合模式的易于解釋性進行更好改進。除此之外, 將現有算法設計成分布式版本，利用Hadoop、Spark進行大規(guī)模數據的序列分類，并將其應用于生物信息領域的數據分析。

致謝感謝周承博士提供的SCIS_HAR和SCIS_MA算法執(zhí)行程序。

參考文獻:

[1]LI Y, LU Y, ZHANG F, et al. Protein classification using family profiles [C]// FSKD 2010: Proceeding of the 7th International Conference on Fuzzy Systems and Knowledge Discovery. New York: ACM, 2010: 2212-2216.

[2]楊旸.基于機器學習方法的生物序列分類研究[D].上海:上海交通大學,2009:1-2. (YANG Y. Research on biological sequence classification based on machine learning methods [D]. Shanghai: Shanghai Jiao Tong University, 2009: 1-2.)

[4]PEARSON W R, LIPMAN D J. Improved tools for biological sequence comparison [J]. Proceedings of the National Academy of Sciences of the United States of America, 1988, 85(8): 2444-2448.

[5]ALTSCHUL S F, GISH W, MILLER W, et al. Basic local alignment search tool [J]. Journal of Molecular Biology, 1990, 215(3): 403-410.

[6]DAO F-Y, YANG H, SU Z-D, et al. Recent advances in conotoxin classification by using machine learning methods [J]. Molecules, 2017, 22(7): 1057.

[7]WEI L, XING P, SHI G, et al. Fast prediction of protein methylation sites using a sequence-based feature selection technique [J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2017, PP(99): 1.

[8]LIU B, XU J, FAN S, et al. PseDNA-Pro:DNA-binding protein identification by combining Chou’s PseAAC and physicochemical distance transformation [J]. Molecular Informatics, 2015, 34(1): 8-17.

[9]熊贇,陳越,朱揚勇.ProFaM:一個蛋白質序列家族挖掘算法[J].計算研究與發(fā)展,2007,44(7):1160-1168. (XIONG Y, CHEN Y, ZHU Y Y. ProFaM: an efficient algorithm for protein sequence family mining [J]. Journal of Computer Research and Development, 2007, 44(7): 1160-1168.)

[10]ZHOU C, CULE B, GOETHALS B. Pattern based sequence classification [J]. IEEE Transactions on Knowledge and Data Engineer, 2016, 28(5): 1285-1298.

[11]MULDER N J, KERSEY P, PRUESS M, et al. In silico characterization of proteins: UniProt, InterPro and Integr8 [J]. Molecular Biotechnology, 2008, 38(2): 165-177.

[12]ZHANG M, KAO B, CHEUNG D W, et al. Mining periodic: patterns with gap requirement from sequences [C]// SIGMOD ’05: Proceeding of the 2005 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2005: 623-633.

[13]WANG X, DUANG L, DDONG G, et al. Efficient mining of density-aware distinguishing sequential patterns with gap constraints [C]// DASFAA 2014: Proceeding of the 2014 International Conference on Database Systems for Advanced Applications, LNCS 8421. Cham: Springer, 2014: 372-387.

[14]TSENG V S, LEE C-H. Effective temporal data classification by integrating sequential pattern mining and probabilistic induction [J]. Expert Systems with Applications, 2009, 36(5): 9524-9532.

[15]LIU B, HSU W, MA Y. Integrating classification and association rule mining [C]// KDD’98： Proceeding of the 4th International Conference on Knowledge Discovery and Data Mining. Menlo Park, CA: AAAI Press, 1998: 80-86.

[16]LIN H, CHEN W. Prediction of thermophilic proteins using feature selection technique [J]. Journal of Microbiological Methods, 2010, 84(1): 67-70.

[17]TANG H, ZOU P, ZHANG C M, et al. Identification of using feature selection technique [J]. Scientific Reports 6, 2016: 30441.

[18]HALL M, FRANK E, HOLMES G, et al. The WEKA data mining software: an update [J]. ACM SIGKDD Explorations, 2009, 11(1): 10-18.