GPS高程擬合方法的探究

張寶蓮

山西省地質勘查局二一二地質隊 山西長治 046000

1 GPS高程擬合的目的和意義

1.1 高程系統

（1）大地高高程系統。大地高高程系統是以參考橢球面為高程基準面的高程系統。地面某點的大地高程H是指由地面點沿通過該點的橢球面的距離。地面點的P的大地高為PP1。

GPS定位測量獲得的是WGS-84橢球大地坐標系中的成果，即GPS測量求得的是點相對于WGS-84橢球的大地高H。

（2）正高高程系統。正高高程系統是以大地水準面為高程基準面的高程系統。地面上任意一點的正高高程Hg是該點沿鉛垂線方向至大地水準面的距離，即

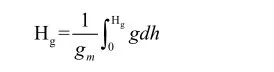
式中：gm為地面點沿鉛垂線至大地水準面的重力加速度平均值。由于gm并不能精確測定，也不能由公式推導出來，所以不能直接求得正高高程。因為正高高程系統是以大地水準面為基準面的高程系統，因而它具有明確的物理意義。大地水準面至橢球面的距離P1P3為大地水準面差距N，即有關系N=H-Hg

（3）正常高高程系統。正高高程實際上無法精確求定，為了使用方便，建立了正常高高程系統。其定義為：

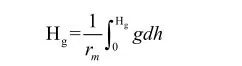
式中：rm為由地面點沿鉛垂線至大地水準面之間的平均正常重力值，可表示為：

式中：r為橢球面上的正常重力，其計算公式為

式中：re為橢球赤道上的正常重力值；β1，β2為與橢球定義有關的系數；φ為地面點的天文緯度。我國目前采用的re，β1，β2值為：re=978.030，β1=0.005302，β2=0.000007。

1.2 GPS高程擬合的意義

由GPS相對定位得到的三維基線向量，通過GPS網平差，可以得到高精度的大地高。如果網中一點或多點具有精確的WGS-84大地高程，則在GPS網平差后，可求得GPS點的WGS-84大地高程。實際應用中，地面點的高程采用正常高系統，是通過水準測量的方法來確定的，這就需要確定大地高與正常高的關系。似大地水準面與參考橢球面間的高差即高程異常，有Hr=H84-，其中Hr為正常高。

高程擬合方法的基本思路是：在GPS網中聯測一些水準點，利用這些點上的正常高和大地擬合高求出它們的高程異常值，再據這些點上的高程異常值與坐標的關系，用最小二乘方法擬合測區的似大地水準面，利用擬合的似大地水準面內插入其它GPS點的高程異常，從而求出各個未知點的正常高。

研究GPS高程的意義有兩個方面，一是精確求定GPS點的正常高，一是求定高精度的似大地水準面。

2 GPS高程擬合方法

2.1 GPS高程測量原理

由高程系統的理論可知，測站點P的大地高H與正常高Hr之間的關系為：Hr=H-式中：為高程異常。若能求出P點的高程異常，就能確定P點的正常高Hr。

GPS高程獲取的方法有多種：（1）繪等值線圖法；（2）狹長帶狀區域線形擬合法；（3）曲面擬合法；（4）地球重力場模型擬合法；5)地球重力場結合GPS水準擬合法。

2.2 等值線圖示法

根據已知點的高程異常值，繪出測區高程異常的等值線圖。然后利用內插算法確定未知點的高程異常。具體做法是：設在某一區域內，有m個GPS點，用幾何水準聯測其中n個點的正常高，根據GPS觀測獲得的點的大地高，求出n個已知點的高程異常。然后，選定適合的比例尺，按n個已知點的平面坐標，展繪在圖紙上，并標注相應的高程異常，再用適當的等高距，繪出測區的高程異常圖。在圖上內插出未聯測幾何水準的(m-n)個點(未聯測幾何水準的GPS點稱為待定點)的高程異常，從而求出這些待定點的正常高。

繪等值線圖示法對于高程異常變化的趨勢比較直觀，使用起來比較簡單。但是高程異常值會受到內插誤差和等值線繪制精度誤差的影響。

2.3 狹長帶狀區域線形擬合法

當GPS點呈線狀布設，在認定沿線似大地水準面為一條連續而光滑的曲線的前提下，可應用解析內插法，求待定點的正常高。其原理是：根據高程控制點的平面坐標及其高程異常值，通過構造一個插值函數來擬合測線方向上的似大地水準面曲線，然后據此內插其它點的高程異常。

實際工程應用中，例如公路中線放樣，鐵路線路勘測等，已知參考點一般不可能布設在公路中線上，反而往往離公路中線數公里外，這樣的GPS數據點實質上并不呈線狀，此時，如果采用線形擬合，其結果肯定是不可靠的。而且，這樣的擬合僅根據測點坐標中的數據之一，如果布設的GPS測點是一條斜線，那么坐標中的X，Y兩個數據都必須考慮，或者用其離中點的距離來表示，這三種數據擬合的結果還是有區別的、不穩定的。總的來說，線性擬合不能夠詳盡地考慮待定點的周圍局部地貌實際情況，參考點的分布，所以擬合結果不可靠。

2.4 曲面擬合法

當GPS點布設成一定區域面時，可以用數學曲面擬合法求定待定點的正常高。其原理是：根據測區中已知點的平面坐標x，y(或大地坐標B，L)和值，用數值法擬合，擬合出測區似大地水準面，再內插出待求點的，從而求出待求點的正常高。

在選擇已知點時，最好選擇那些高程異常變化比較顯著的點，這些點能很好描述該區域內高程異常分布的特征，最好位于最高，最低以及坡度變化處。這種擬合法最大的問題來自于和核函數的選取，需要不斷試驗改進選取。通過多次試驗比較，才能取得最理想的擬合效果。對于雙曲面來說，一般說來，越大，內插的曲面越平滑。對于倒雙曲面，要求δ必須大于零，否則可能無法求解。

2.5 地球重力場模型擬合法

地球重力場模型是根據衛星跟蹤數據、地面重力數據、衛星測高數據等重力場信息，由地球撓動位的球諧函數級數展開式求高程異常ξ，結合GPS求出的大地高，再求出點的正常高的一種方法。

由物理大地測量學可知，地面點P的撓動位T與該點引力位V和正常引力位U之間的關系為：T=V-U而地面點P的高程異常為ξ：ξ=T/r式中，r為地面點P的正常重力值。正常重力值r和正常引力位U可以精確計算，因此只要給出地面點P的引力位V。就可求出地面點P的高程異常ξ。

引力位V可由球諧函數級數展開式計算：

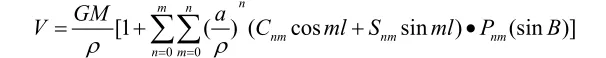
式中，ρ，B，L為地面點的矢徑、緯度、經度；Cnm,Snm為位系數；Pnm(sinB)為勒讓德函數；n為階；m為次。

當n越趨向無窮大，上式越趨于正確。目前，國際上n已求到360階次。我國WDM-89模型，除利用國外資料外，用了我國5萬多個重力點資料，用WDM-89模型，在沿海平原地區計算ξ可達到厘米級精度，山區為0.2米精度，其他地區為1.0-1.5米左右，這是重力點密度不足所致。

2.6 地球重力場結合GPS水準擬合法

從目前我國實際情況來看，GPS重力高程的精度低于GPS水準高程精度。故采用重力場模型和GPS水準相結合的方法是一條有效的途徑。

該方法的基本思路是：在GPS水準點上，將由GPS大地高程和水準正常高求得的高程異常ξ與由重力場模型求得的高程異常ξm進行比較，求出該地面點的兩種高程異常的差值：Δξ=ξ-ξm，然后再采用曲面擬合方法，由公共點的平面坐標和Δξ推求其他點的Δξ，由此計算GPS網中未聯測水準點的正常高程：h=H-ξm-Δξ

3 結論

高程擬合是一件復雜的工作，對于我國地形變化實際情況，沒有一種模型能普遍適用于各種地形，因此擬合GPS高程異常時應該根據地形變化以及控制點的數量、分布情況靈活的選擇擬合模型。還可以綜合幾種方法進行擬合，通過綜合分析比較，得到以下結論：

（1）狹長線形區域地形擬合模型中，正交函數擬合模型、最小二乘法三次曲線擬合效果比較好。多項式曲線擬合模型不適用于控制點較多的情況。擬合次數不宜過高，否則曲線振蕩太厲害，不能較準確的反映高程異常起伏的狀況。

（2）平坦地區的擬合過程中，平面擬合模型效果要優于平面相關擬合模型。這種擬合模型適用于測區面積較小，控制點的數目較少且地形變化較為平緩的地區。由于這種地形高程異常變化比較平緩，因此在選擇控制點時控制點要選擇在那些高程異常變化的極值點處和一些高程異常變化較明顯的點位。否則平面擬合的精度將大打折扣，另外選擇還要注意點位分布均勻，便于從整體上進行擬合插值計算。

（3）丘陵地區高程異常變化較為劇烈，因此二次曲面擬合效果不是很理想。但是最小二乘法曲面擬合模型和多面函數擬合模型擬合精度比較理想。如果已知數據點比較充分，可以適當增加控制點，這樣最小二乘曲面擬合模型的精度會得以提高。

（4）較大區域地形或者過于狹長的地形，由于高程異常變化大，不宜用一種擬合模型。應該根據高程異常變化綜合利用幾種擬合模型分區域進行擬合。控制點的選擇除了選擇在一些地形特征點外，還要注意分布均勻，便于擬合。另外即使在某一特定區域，也要選擇幾種適當的方法進行擬合，以便對數據進行分析比對。

（5）在選用合適的擬合模型后，擬合的精度可以達到四等水準精度。可以用于一般工程的碎部高程控制。但是不宜作為高等級控制高程點。