激活 積累 提升 應用

胡余芳

[摘 要]數學基本活動經驗是學生在經歷數學活動的過程中，產生和形成的感受、體驗和感悟。以“組合圖形的面積計算”的教學為例，從激活、積累、提升、應用四個方面談談如何幫助學生獲得數學基本活動經驗，以便更好地開展有效的教學。

[關鍵詞]數學基本活動經驗；激活；積累；提升；應用

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2018）08-0018-02

數學基本活動經驗是學生在經歷數學活動的過程中，產生和形成的感受、體驗和感悟。如何讓學生獲得數學基本活動經驗？筆者認為：找準學生的認知起點，為學生激活新經驗打下認知和情感的基礎；創(chuàng)設有效的數學活動，為學生積累活動經驗提供直觀性感受；適度地提煉方法，為學生形成新的活動經驗給予及時的提升；加強綜合性應用，為學生運用新的活動經驗提供更為廣闊的舞臺。

下面以“組合圖形的面積計算”的教學為例，試拋教學反思之磚，以引經驗分享之玉。

一、找準認知起點，激活經驗

杜威曾說：“教育就是經驗的改造或重組。”這就是說，一個新知的獲得，都是建立在原有的經驗基礎之上，只有通過經驗的改造和重組，才能形成新的數學活動經驗。因此，找準學生的認知起點，讓原有經驗支撐學習活動，才能為學生激活新的活動經驗打下認知和情感的基礎。

活動一：復習導入，認識組合圖形

1.復習學過的平面圖形，回顧它們的面積計算方法。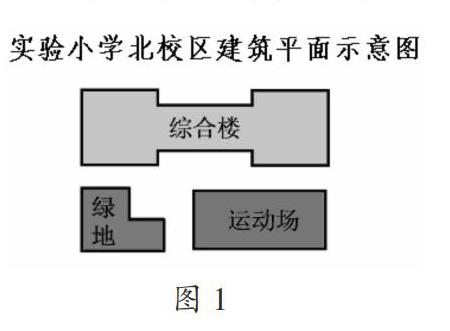

2.出示組合圖形（圖略），與簡單的平面圖形進行對比，引出“像這樣由簡單圖形組成的圖形就是組合圖形。”

3.判斷生活中的組合圖形（北校區(qū)建筑平面示意圖），介紹輔助線。

數學具有嚴密的邏輯性和系統(tǒng)性，學生之前積累的經驗，對后續(xù)學習有著重要的指導意義。在這一活動中，“復習學過的平面圖形，回顧它們的面積計算方法”能喚起學生對已有知識的回憶。活動一雖沒有熱鬧的場面，但卻幫助學生對舊知進行了鞏固，為學生學習新知打下了扎實的基礎。“出示組合圖形，并與簡單的平面圖形進行對比”有效地激活了學生對于組合圖形的認知，“判斷生活中的組合圖形，介紹輔助線”，又為積累“組合圖形面積計算”的活動經驗起到了指明方向和指導方法的作用。

二、創(chuàng)設有效活動，積累經驗

數學基本活動經驗的獲得離不開有效的數學活動。課程標準指出：數學教學活動，特別是課堂教學，應能激發(fā)學生的學習興趣，調動學生的學習積極性，引發(fā)學生的數學思考，鼓勵學生的創(chuàng)造性思維。學生應當有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程。因此，把學生應習得的數學經驗融入可操作、能體驗的數學活動中，就能為學生積累活動經驗提供更多的直觀感受。

活動二：探索交流，學習組合圖形的面積計算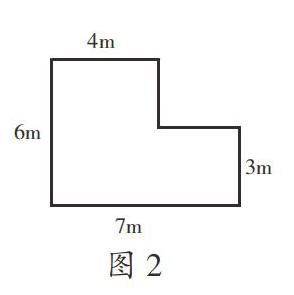

1.創(chuàng)設情境：由圖2的綠地鋪草皮問題引出如何求組合圖形的面積，并揭題。

2.自主探索，交流方法

（1）想：根據老師提供的數據，想一想你準備怎樣計算圖1的面積。

（2）做：把想到的方法先在圖上畫一畫，再計算。

（3）反饋交流方法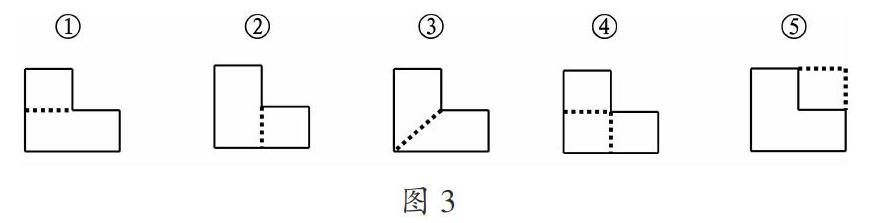

為學生創(chuàng)設一個開放的探究空間，能保證每個學生都參與活動，獲得直觀感受。在這一活動中，重點是對例題進行處理：人教版教材安排的例題是計算房屋側面積，但學生只能想到分割成一個三角形和一個長方形，以及分割成兩個梯形兩種解題方法，想法顯然不夠豐富，如果不能把分割法和添補法整合在一起教學，就無法讓學生很好地體驗各種方法的優(yōu)劣。因此，筆者選了北師大版教材的例題，將其調整數據后就作為新課展開的載體，借其相應的豐富的解題方法，拓寬學生的思維，使學生在數學活動的“過程”和“經歷”中獲得多元的數學活動經驗。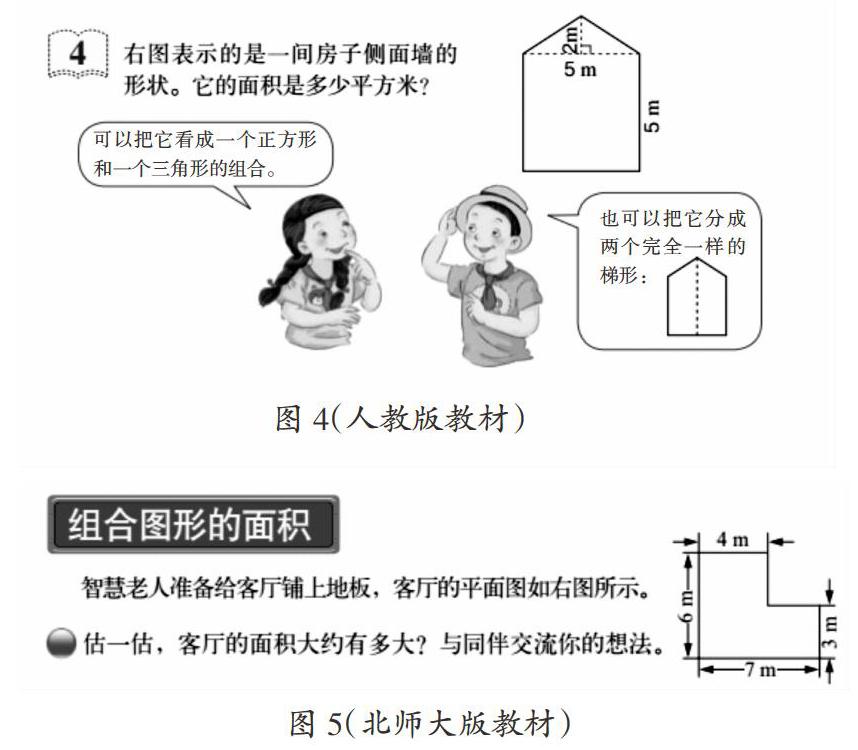

三、適度提煉方法，提升經驗

愛因斯坦曾說：“一切關于實在的知識，都是從經驗開始，又終結于經驗。”這說明：如果僅限于直觀感受所獲得的經驗，這只能算是低級的思維活動。因此，要想使低級的思維活動上升到高級水平，就要適度地對方法進行提煉，引領學生提升所獲得的活動經驗，使經驗從“特殊”推廣到“一般”。

活動三：觀察對比，方法分類

1.引導發(fā)現(xiàn)：

（1）把組合圖形分割成幾個簡單圖形，稱為分割法。把分割后的簡單圖形的面積相加就是組合圖形的面積；補上一塊的方法稱為添補法，可以用求差的方法算出組合圖形的面積。

（2） 無論是分割法和添補法，目的都是將組合圖形轉化成已學過的簡單圖形，所以轉化是數學的一種重要的思想方法。

2.優(yōu)化方法：分割和添補的圖形越簡單，計算就也越容易。

有效的數學學習應當是以數學思維活動為核心的。在小學數學教學階段，有意識地引導學生提煉一些基本數學思想方法是提高學生數學能力和思維品質的重要手段，是從傳授知識到培養(yǎng)學生分析問題、解決問題能力的重要途徑，也是小學數學教學進行素質教育的真正內涵所在。在活動三中，學生豐富和積累了兩個方面的數學活動經驗：一是認識到分割和添補是兩種計算組合圖形面積的常用方法；二是運用方法解決問題要靈活多變，要根據問題的特點和提供的信息進行選擇。學生獲得的新的活動經驗具有更廣泛的適用性和更高層次的概括性，為解決其他的組合圖形面積問題提供一般的解決方法。

四、加強綜合應用，運用經驗

數學基本活動經驗源于數學活動，又應用于現(xiàn)實生活，并會隨著學生的實踐活動不斷豐富、不斷發(fā)展。因此，加強綜合性應用，能為學生運用新經驗提供更為廣闊的舞臺，能引導學生學以致用，提高學生的實踐能力。

活動四：鞏固練習

1.基本練習：圖6是一間房子的側面墻。它的面積是多少平方米？

2.提高練習，引導學生發(fā)現(xiàn)：

（1）選擇用哪種方法來計算組合圖形的面積時，不僅要根據圖形的特點，還要考慮有沒有數據的問題。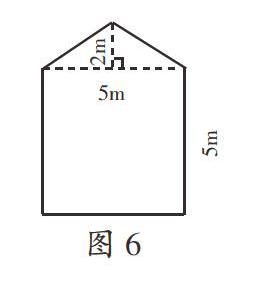

（2）計算組合圖形的面積不僅可以用分割法、添補法，還可以把分割和添補結合起來，用割補法來求。

（3）在圖7-1、7-2、7-3中，任選一個圖形進行面積的計算。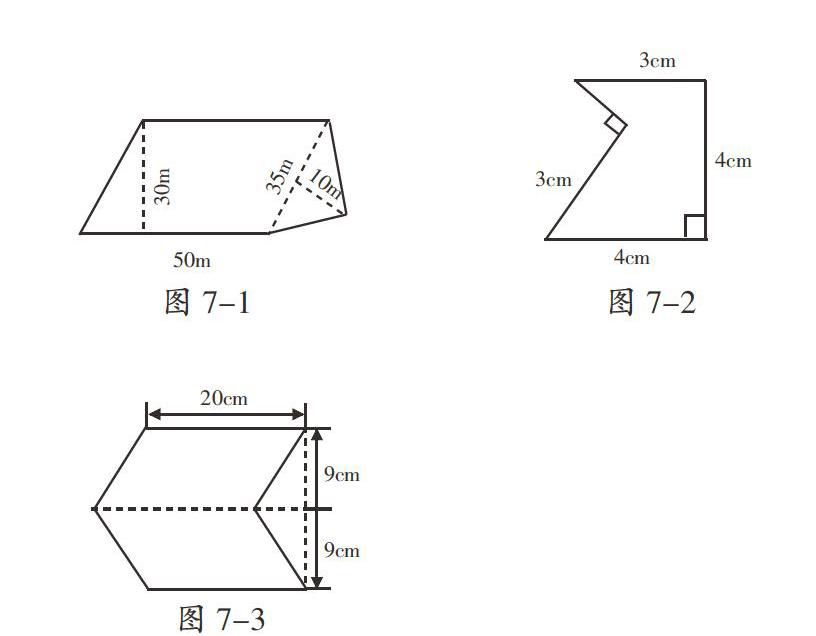

3. 綜合練習：用多種方法解答做一面中隊旗要用多少布料。綜合運用各種方法解題，并交流反饋。

運用數學活動經驗解決實際問題，就能把原本屬于認知層面的單一的數學活動經驗提高到實踐層面的綜合性數學活動經驗，能有效提升學生的應用意識。在活動四中，有三個層次的練習：

（1）基本練習：計算一間房子側面墻的面積。訓練學生運用分割法解題，同時也引導學生在求組合圖形面積時學會正確選擇數據。

（2）提高練習：三個組合圖形的面積計算。讓學生在選擇方法計算組合圖形的面積的過程中明白，不僅要根據圖形的特點選擇，還要考慮有沒有數據的問題，從而學會靈活運用各種方法求組合圖形的面積。

（3）綜合練習：計算中隊旗的面積。進一步鞏固分割法和添補法的運用，引導學生用多種方法求組合圖形的面積，培養(yǎng)學生一題多解的能力，以及讓學生能夠綜合運用本節(jié)課學到的知識解決問題。

這樣，學生不但學會了用基礎的方法解題，還能通過拓展延伸的練習，得到了靈活運用各種方法解決實際問題的機會，真正達到運用活動經驗的目的。

總之，數學基本活動經驗的獲得，是學生建構知識體系、形成學科基本素養(yǎng)和能力的重要前提，也是全面提升學生思維水平，促進學生數學思想方法形成的一個重要途徑。教師只有不斷探索，才能真正找到幫助學生積累數學活動經驗的方法，從而培養(yǎng)學生終身受用的數學素養(yǎng)。

（責編 金 鈴）