雙滲四重介質壓力動態分析

姬安召，王玉風，崔建斌

(1.隴東學院能源工程學院，甘肅慶陽 745000；2.隴東學院數學與統計學院，甘肅慶陽 745000)

由于碳酸鹽巖受沉積環境與成巖后生作用等不同程度的影響，儲層的孔隙復雜，裂縫形態多樣，形成多級別、多開度的裂縫與溶蝕縫，該特征導致碳酸鹽巖巖性油氣藏的滲流規律具有復雜性[1，2]。目前，許多學者對縫洞型碳酸鹽巖儲層的滲流規律進行了研究。賈永祿等[3]建立了基巖、溶蝕孔洞、微裂縫和大裂縫的四孔單滲模型，并采用Laplace變換和Stehfest數值反演方法進行了求解，但只考慮了微裂縫、基巖和溶蝕孔洞向大裂縫竄流，井筒供液只有大裂縫提供，沒有考慮介質間流體的流動。程時清、顧岱鴻、張利軍、常學軍等[4-7]建立了基巖、溶洞和裂縫三重介質的數學模型，并用Laplace變換等數學方法進行了模型的求解，通過數值反演的方法繪制了三重介質試井曲線，并對曲線的特征進行了分析。趙玉龍等[8]對三重介質油藏非牛頓流體的冪律流規律做了研究。任俊杰等[9]研究斜井三重介質井底壓力動態特征，當井斜角大于60°時，早起垂向徑向流的壓力導數曲線為一條水平線，井斜角小于60°時，與直井的壓力動態特征一致。楊堅等[10]對斜井三重介質油藏的單井壓力動態特征進行了研究，分別考慮了無限大邊界，封閉邊界和定壓邊界的情況。張冬麗等[11-13]研究了縫洞型碳酸鹽巖油藏油水兩相滲流三重介質的數值試井方法。總結前人研究成果，本文主要針對大裂縫、微裂縫和溶蝕孔洞發育的復雜儲層碳酸鹽巖油藏，建立以大裂縫和微裂縫向井筒供液的雙滲四重介質數學模型，并對采用Laplace變換及含有特征參數的微分方程通解分析的方法進行模型求解，然后采用Stehfest數值反演進行典型曲線的繪制，并對影響典型曲線特征的因素進行分析。

1 四孔雙滲物理模型

儲層由溶蝕孔洞、大裂縫、微裂縫和基巖組成，儲層中的大裂縫和微裂縫為流體的流動提供了滲流通道，溶蝕孔洞和基巖提供了主要的儲存空間。該模型描述了大裂縫和微裂縫共同向井筒供液，溶蝕孔洞和微裂縫的流體向大裂縫發生竄流，同時基巖的流體也向溶蝕孔洞發生竄流，具體物理模型(見圖1)。

為了簡化大裂縫、微裂縫、溶蝕孔洞和基巖滲流的數學模型，基本假設為：油井以定產量生產；儲層流體和儲層巖石微可壓縮，并且為單相流體；儲層流體在這四種介質中的流動符合達西滲流規律；考慮井筒儲集效應和表皮效應的影響；忽略重力和毛管力的影響；地層的啟動壓力很小，忽略不計；每一種介質的滲透率、孔隙度和壓縮系數相互獨立；流體只通過大裂縫和微裂縫流向井筒，溶蝕孔洞和基巖作源。

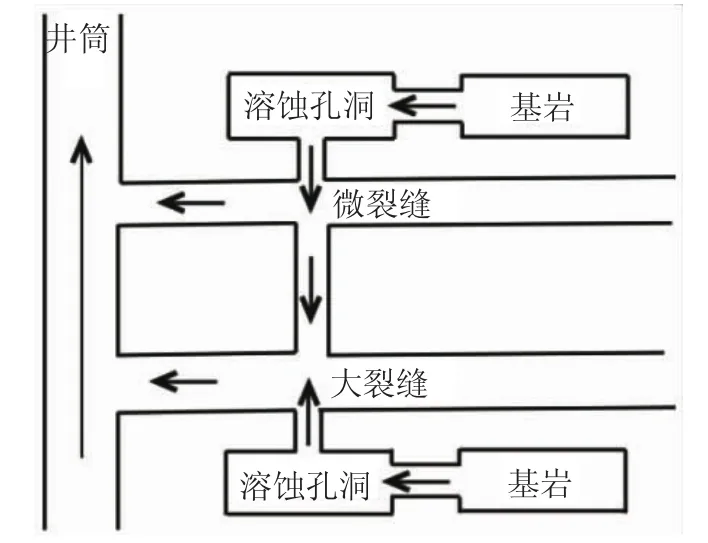
圖1 四孔雙滲模型示意圖

2 四孔雙滲數學模型建立與求解

2.1 模型的無因次滲流微分方程

基于以上物理模型，根據儲層流體的運動方程、質量守恒方程和狀態方程，建立法定單位下的無因次大裂縫、微裂縫、溶蝕孔洞與基巖連通情況下的滲流數學模型。

無因次大裂縫滲流微分方程：

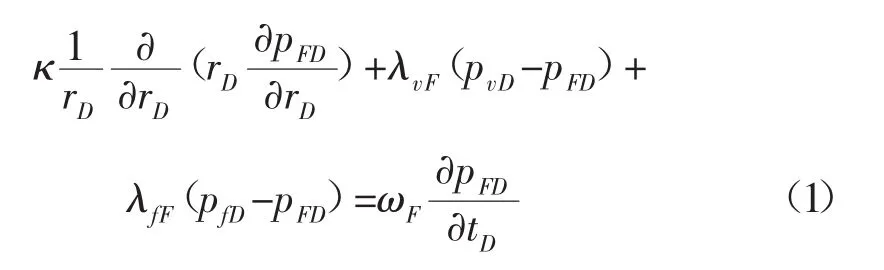
無因次微裂縫滲流微分方程：

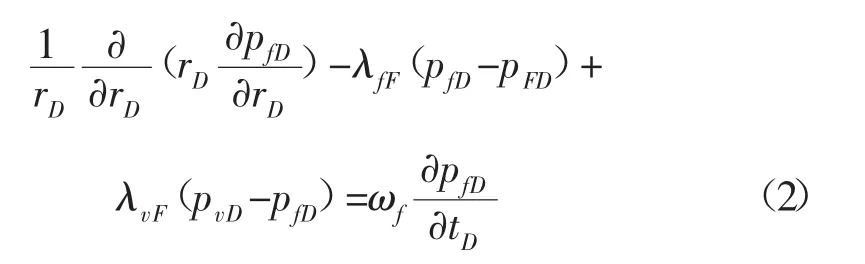
無因次溶蝕孔洞滲流微分方程：

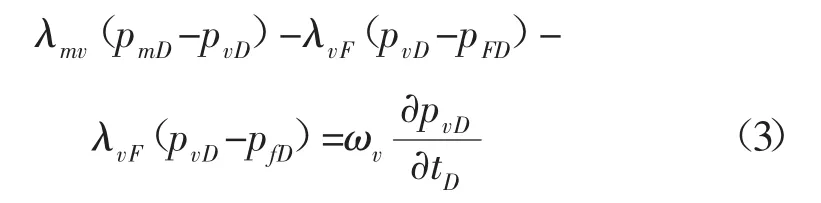
無因次基巖滲流微分方程：

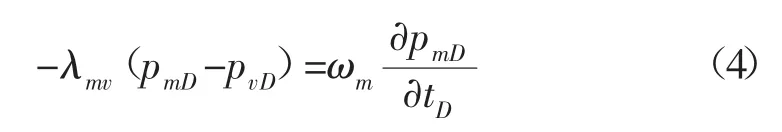
為了簡化模型的求解，無因次參數定義如下：無因次半徑的定義：

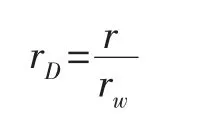
無因次時間的定義：

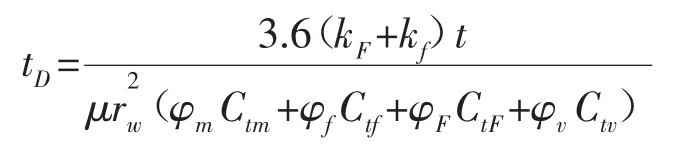
無因次壓力的定義：

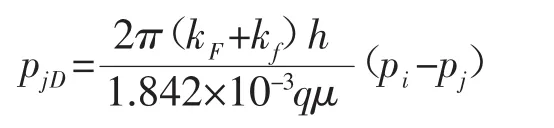
式中：下標 j=F，f，v，m；F-大裂縫；f-微裂縫；v-溶蝕孔洞；m-基巖。

無因次井儲系數的定義：

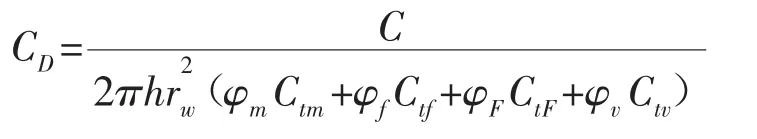
不同介質的彈性儲容比的定義：

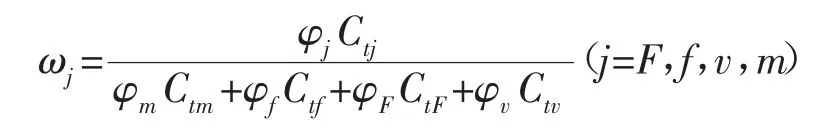
不同介質之間的竄流系數：

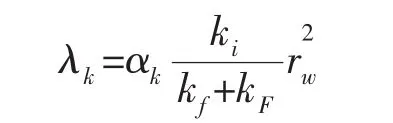
式中：下標 k=fF，vF，vf，mv；分別表示微裂縫向大裂縫竄流、溶蝕孔洞向大裂縫竄流、溶蝕孔洞向微裂縫竄流和基巖向溶蝕孔洞竄流，其對應的下標i=f，v，v，m。

滲透率比值的定義：

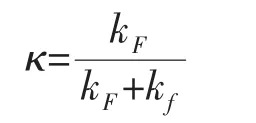
式中：r-井距儲層中任意位置的距離，m；kj-四種介質的滲透率，μm2；μ-儲層流體的黏度，mPa·s；pj-四種介質儲層流體的壓力，MPa；αk-形狀系數，m-2；φj-四種介質的孔隙度，無量綱；Ctj-四種介質的綜合壓縮系數，MPa-1；t-時間，h。

無因次初始條件為：

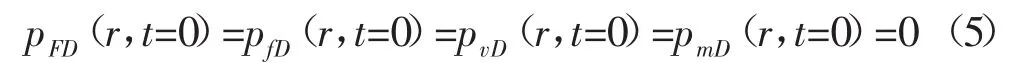
無因次井底定產條件為：

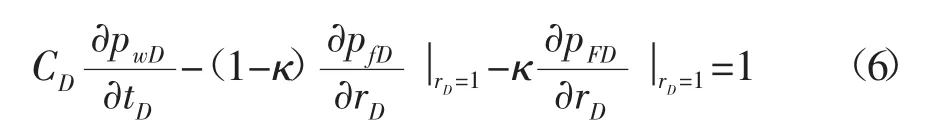
無因次表皮效應的內邊界條件為：

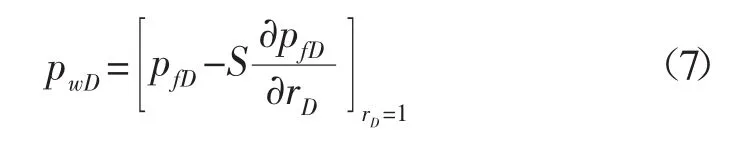
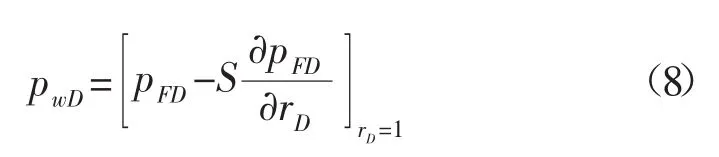
無因次無限大外邊界條件為：

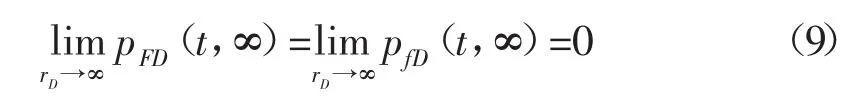
無因次封閉外邊界條件為：

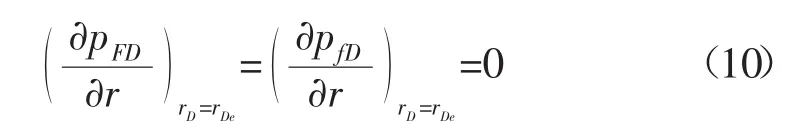
無因次定壓外邊界條件為：

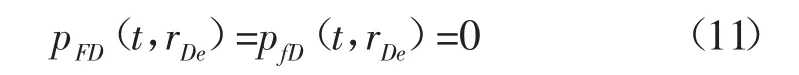
式中：rDe-無因次外邊界半徑。

為了求解(1)～(11)式定解微分方程，對(1)～(11)式的無因次時間tD變量進行Laplace變換，在Laplace空間的變量用z表示，壓力用pˉ表示。

2.2 微分方程特征參數求解

對溶蝕孔洞和基巖滲流微分方程(3)和(4)式進行Laplace變換，同時考慮(5)式的初始條件，經過Laplace變換可化簡為代數方程，在代數方程中，用大裂縫和微裂縫的Laplace空間無因次壓力分別表示基巖和溶蝕孔洞的壓力。將這兩個方程代入大裂縫和微裂縫Laplace空間的滲流微分方程中，通過整理可得：

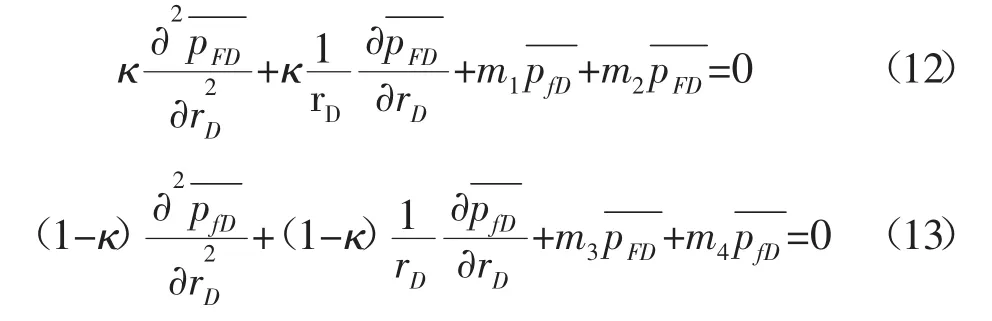
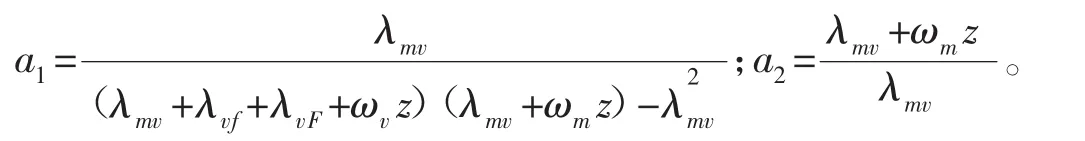
根據文獻[8]，在無限大外邊界的條件下方程(12)和(13)式的通解為：

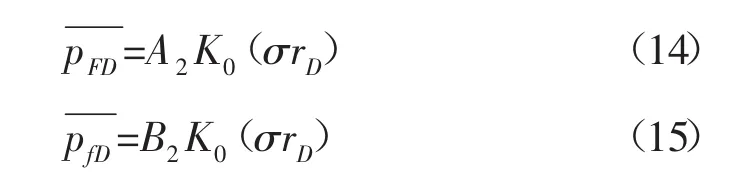
式中：K0(σrD)-修正的零5第二類Bessel函數；σ-特征參數；A2、B2-滿足內邊界的待求參數。

將(14)和(15)式分別代入到(12)和(13)式，可得到關于A2和B2的線性方程組。由實際問題可知，A2和B2是存在的，則齊次線性方程組的系數矩陣的行列式的值為0。通過整理可得關于特征參數σ的方程為：

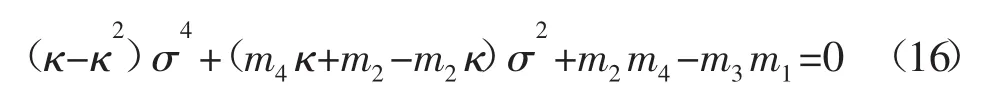
通過(16)式可知特征參數σ有兩個實數解σ1和σ2，根據線性微分方程解的疊加原理，這兩個特征參數共同構成了微分方程的解，則微分方程的通解(14)和(15)式又可表示為：

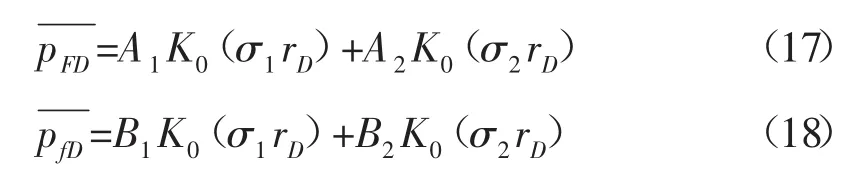
式中：A1、B1、A2和B2為滿足內邊界的待求參數。

將(17)和(18)式代入到(12)和(13)式，結合修正Bessel函數 K0(x)的導數，可得關于 A1、B1、A2和 B2四個未知參數的兩個方程組。這兩個方程組中含有修正Bessel函數 K0(σ1rD)和 K0(σ2rD)，由于 σ1和 σ2是互異的，則K0(σ1rD)與K0(σ2rD)是線性無關的，要是方程組有解，則K0(σ1rD)與K0(σ2rD)的系數之和必須為0，通過整理可得 A1、B1、A2和 B2四個未知參數關系[14]。則Laplace空間微裂縫滲流微分方程的通解為：

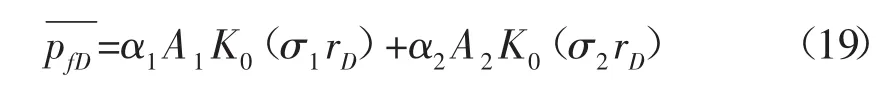
2.3 無限大地層模型的解

根據(17)和(19)式可知，要得出微分方程的特解，則需要兩個條件即可。對于無限大地層而言，外邊界條件在方程通解給出的過程中已經使用，現在將(17)和(19)式代入到內邊界定產條件(6)式和表皮效應條件(7)和(8)式，通過整理可得：

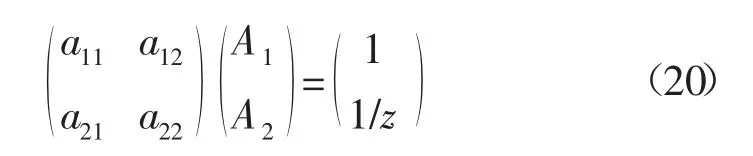
式中：

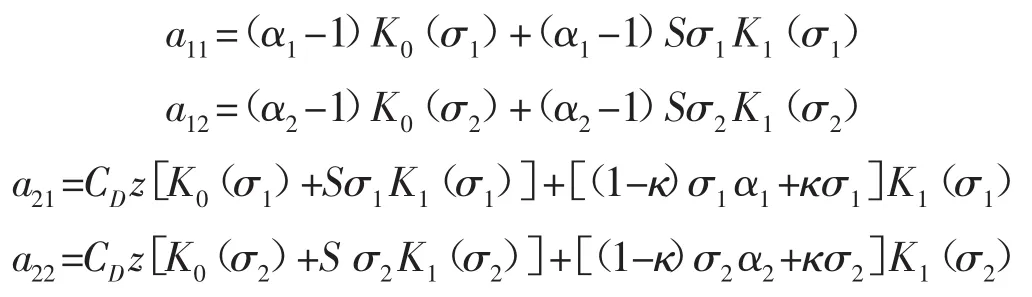
通過(20)式的求解，可得滿足內邊界條件的參數A1和A2。根據獲得Laplace空間的解析解，采用Stehfest數值反演方法可得實空間的井底壓力。

2.4 封閉邊界與定壓邊界模型的解

對于封閉邊界和定壓邊界求解過程與上述思路相同，只是受邊界條件的影響，方程的通解形式不同。限于篇幅有限，這里只給出本文求解的結果。

井底壓力的表達式為：

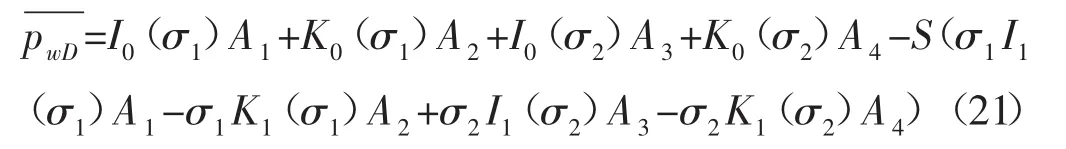
式中：特征參數σ1和σ2由(16)式確定，方程系數A1、A2、A3和 A4由下列方程組確定：

對于封閉邊界而言，其系數為：

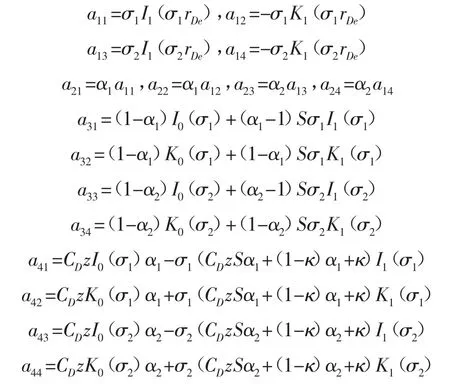
對于定壓邊界而言，只有系數a11、a12、a13和a14不同，其他同封閉邊界：

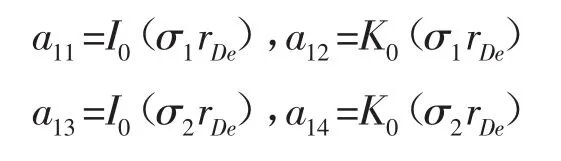
3 壓力動態分析

3.1 流動5段的劃分

雙滲四重介質油藏試井曲線劃分為5個5段(見圖2)：AB段是早期的井儲5段，曲線的特征為45°線，井儲結束后，井底壓力導數曲線出現峰值，之后向下傾斜，這個特征是表皮效應的響應特征；BE段出現了3個“凹子”是流體在介質間竄流的結果，BC段是微裂縫和溶蝕孔洞向大裂縫的竄流5段，CD段是溶蝕孔洞向微裂縫的竄流5段，DE段是基巖向溶蝕孔洞的竄流5段；EF段是邊界的響應特征，對于井底壓力導數曲線而言，在無限大邊界中表現為水平的0.5線，在封閉邊界中表現為上傾的45°線，在定壓邊界中導數曲線下降很快。圖2中的無因次井儲系數CD為1.0，表皮系數S為5.0，滲透率比κ為0.95，基巖彈性儲容比ωm為0.7，溶蝕孔洞彈性儲容比ωv為0.2，微裂縫彈性儲容比ωf為0.08，大裂縫彈性儲容比ωF為2×10-3，微裂縫向大裂縫竄流系數λfF為1×10-4，溶蝕孔洞向大裂縫竄流系數λvF為1×10-6，溶蝕孔洞向微裂縫竄流系數λvf為8×10-7，基巖向溶蝕孔洞竄流系數 λmv為 1×10-8，封閉邊界和定壓邊界的無因次半徑rDe為2×10-4。

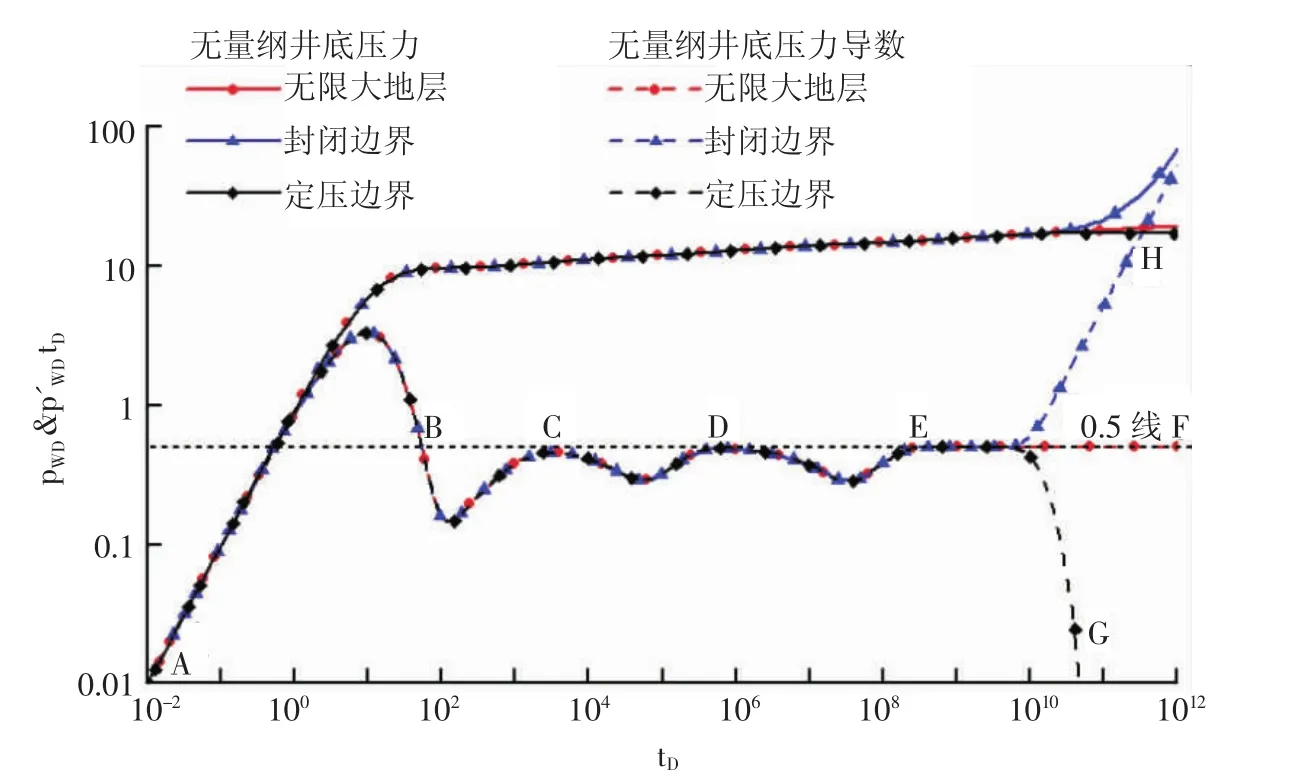
圖2 不同邊界井底壓力與壓力導數曲線

3.2 彈性儲容比(ω)

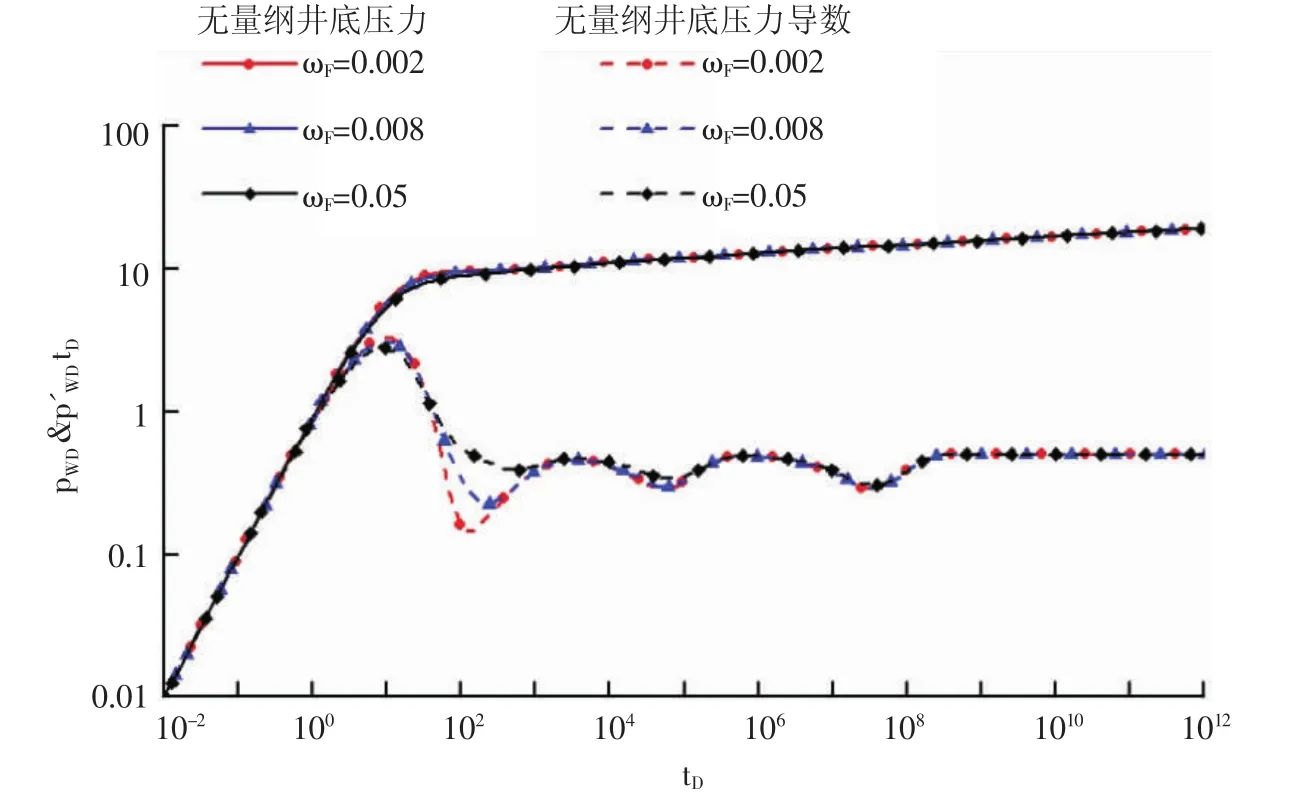
圖3 彈性儲容比對壓力導數曲線形態的影響

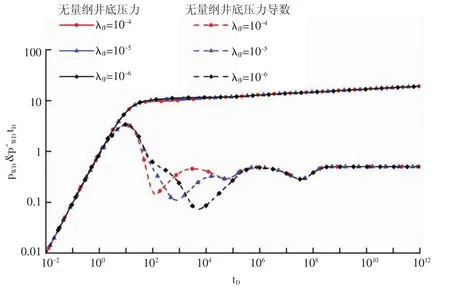
圖4 竄流系數對壓力導數曲線形態的影響

彈性儲容比是用來描述大裂縫、微裂縫、溶蝕孔洞和基巖的彈性儲容能力相對大小的物理量。彈性儲容比主要影響試井曲線“凹子”的深度和寬度。當大裂縫彈性儲容比ωF逐漸增大時(見圖3)，第1個“凹子”就逐漸變淺且變窄，同時對第2個“凹子”也變淺且變窄，但影響較小，對第3個“凹子”基本沒有影響。圖3中的參數取值與圖2中參數取值一致。

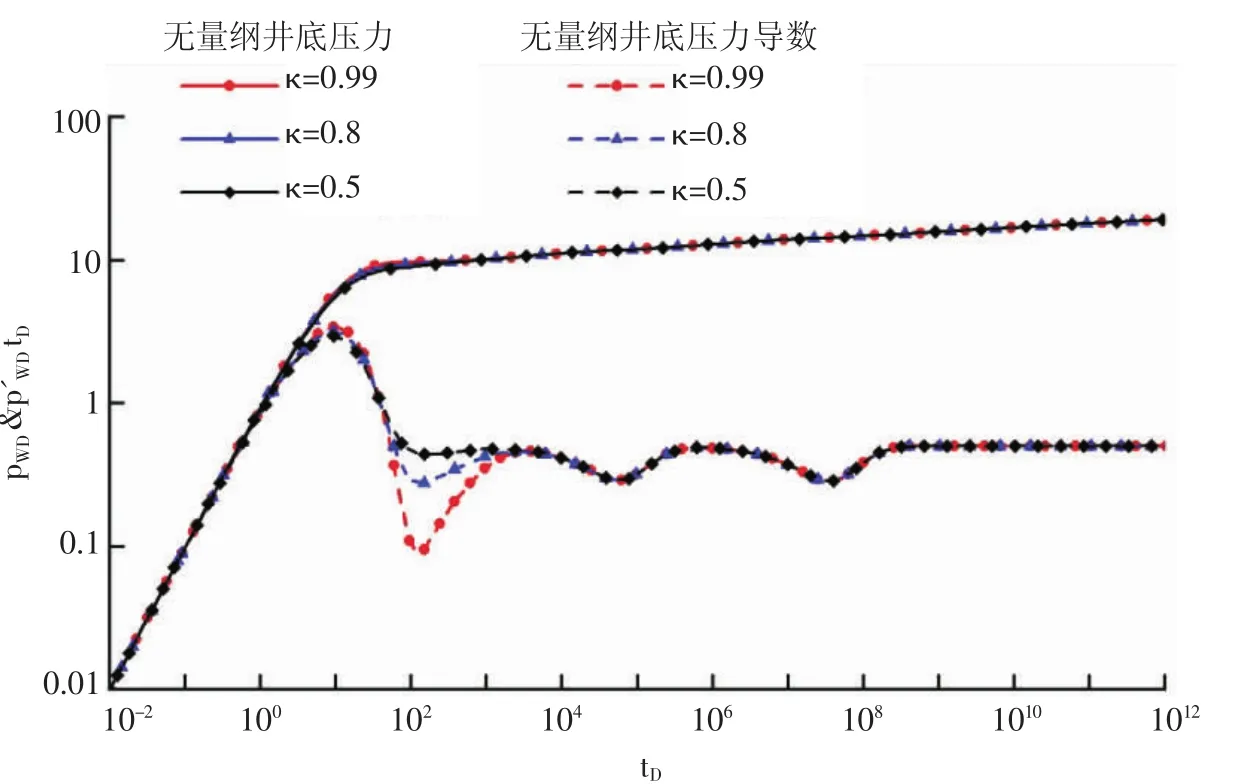
圖5 滲透率比對壓力導數曲線形態的影響

3.3 竄流系數(λ)

在雙滲四重介質油藏中，大裂縫、微裂縫、溶蝕孔洞與基巖之間存在著流體交換，竄流系數就是用來描述四種介質間流體交換的物理量，它反映介質間竄流的能力。竄流系數的大小決定壓力導數曲線的過渡段“凹子”出現的時間，同時竄流系數也能影響到“凹子”的深度及寬度。當微裂縫向大裂縫竄流系數逐漸減小時，“凹子”出現的時間越晚，并且“凹子”越寬越深(見圖4)。圖4中的溶蝕孔洞向大裂縫竄流系數λvF為1×10-6，當微裂縫向大裂縫竄流系數與λvF相等時，這表明微裂縫與溶蝕孔洞向大裂縫竄流的能力是一樣的，壓力導數曲線表現出三種介質的性質，即在圖4中出現了兩個“凹子”。

3.4 滲透率比(κ)

滲透率比主要影響壓力導數曲線的第1個“凹子”的深度(見圖5)，滲透率比與大裂縫彈性儲容比都是決定第1個“凹子”的深度，但滲透率比越大，第1個“凹子”越深。若滲透率比等于0.5，表明大裂縫和微裂縫的滲流能力是一致的，二者可以看作是一種介質，這時就可以簡化為三重介質，則壓力導數曲線由原來的三個“凹子”變為兩個“凹子”。

4 結論

(1)對含有特征參數的滲流微分方程通解與微分方程的構成條件進行分析，求解出雙滲四重介質模型的解析解。

(2)雙滲四重介質試井中壓力導數曲線出現了三個“凹子”，這對雙滲四重介質油藏試井分析的研究與應用具有一定的借鑒意義。

(3)壓力導數曲線上“凹子”的數量與大小主要由介質間竄流系數，介質的彈性儲容比以及滲透率比共同來決定，這些參數的取值對壓力導數曲線形態的影響較為敏感，只有當各個參數選取都十分恰當時，才能表現出每個5段的滲流特征。

參考文獻：

［1］王龍，等.碳酸鹽臺地的類型、特征和沉積模式-兼論華北地臺寒武紀陸表海-淹沒臺地的沉積樣式［J］.地質論評，2018，64(1)：62-76.

［2］付坤榮，等.塔中地區晚奧陶世碳酸鹽臺緣與臺內沉積差異-定性和定量的碳酸鹽巖微相綜合分析［J］.沉積學報，2018，36(1)：101-109.

［3］賈永祿，孫高飛，聶仁仕，等.四重介質油藏滲流模型與試井曲線［J］.巖性油氣藏，2016，28(1)：123-127.

［4］程時清，屈雪峰.三重介質模型試井分析方法［J］.油氣井測試，1997，12(1)：5-11.

［5］顧岱鴻，丁道權，劉軍.三重介質頁巖氣藏分段壓裂水平井產能預測模型［J］.大慶石油地質與開發，2016，35(1)：158-165.

［6］張利軍，程時清，尹洪軍.雙滲三重介質油藏試井分析［J］.特種油氣藏，2008，13(5)：66-69.

［7］常學軍，姚軍，戴衛華，等.裂縫和洞與井筒連通的三重介質油藏試井解釋方法研究［J］.水動力學研究與進展(A輯)，2004，23(3)：339-346.

［8］趙玉龍，張烈輝，青勝蘭.三重介質油藏非牛頓冪律流體試井模型與典型曲線分析［J］.水動力學研究與進展(A輯)，2010，25(2)：254-261.

［9］任俊杰，郭平，汪周華.三重介質油藏斜井壓力動態特征分析［J］.水動力學研究與進展(A 輯)，2012，27(1)：7-15.

［10］楊堅，姚軍，王子勝.三重介質復合油藏壓力動態特征研究［J］.水動力學研究與進展(A 輯)，2005，13(4)：418-425.

［11］張冬麗，李江龍，杜文軍，等.縫洞型油藏三重介質油水兩相流數值試井解釋方法［J］.水動力學研究與進展(A輯)，2010，25(4)：429-437.

［12］張冬麗，李江龍，吳玉樹.縫洞型油藏三重介質數值試井模型［J］.西南石油大學學報(自然科學版)，2010，32(2)：82-88.

［13］張冬麗，李江龍，吳玉樹.縫洞型油藏三重介質數值試井模型影響因素［J］.西南石油大學學報(自然科學版)，2010，32(6)：113-120.

［14］孔祥言.高等滲流力學［M］.合肥：中國科技大學出版社，2010.