汽車零部件三維裝載問題研究

林永昊 姚明山 趙 磊，3 朱道立，3

（1.上海交通大學 中美物流研究院，上海 200030；2.同濟大學 經濟與管理學院，上海 200092；3.上海交通大學 安泰經濟與管理學院，上海 200030）

1　問題描述

汽車零部件三維裝載問題是指對給定一輛待配載貨車以及一批待裝貨物，確定一個可行的裝載方案使得在滿足約束條件（貨物不與車廂相嵌約束；貨物互不相嵌約束；貨物承重約束等）下，車輛裝載率（裝入貨車的所有貨物體積之和／貨車車廂體積*100%）最大。

該問題滿足如下假設條件：

（1）車廂及待裝貨物均為長方體；

（2）放入的貨物完全被包含在車廂內；

（3）貨物只能以棱平行（或垂直）于車廂的棱的方向放置；

（4）貨物只能繞高度棱旋轉，不可傾倒放置。

如圖1所示，以面向車頭方向車廂左前角作為坐標原點建立笛卡爾坐標系，待裝貨物的裝載位置由其最靠近坐標原點的角點坐標值表示，則可行裝載方案中各已裝入貨物的裝載位置可用貨物的角點坐標值表示。

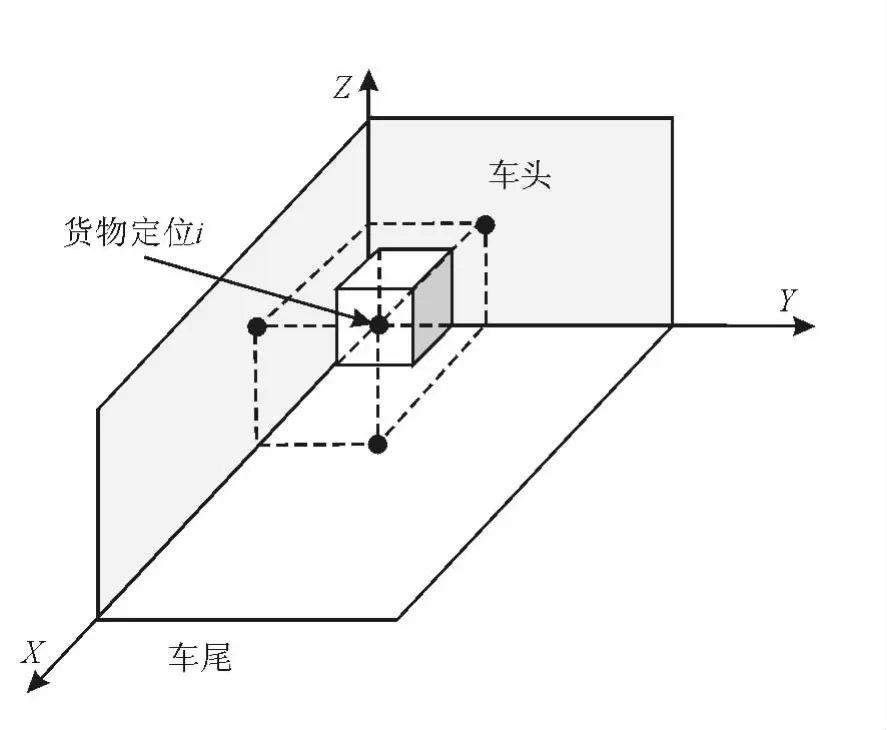
圖1　坐標系示意圖

在圖1所示建立坐標系下，汽車零部件三維裝載問題的數學模型可表示如下：

1.1　集合

I=｛1，…，N｝：待裝載貨物的集合。

1.2　參數

Li：貨物i的長度，i∈I；

Wi：貨物i的寬度，i∈I；

Hi：貨物i的高度，i∈I；

Qi：貨物i的重量，i∈I；

Vi：貨物i的體積，i∈I，Vi=Li×Wi×Hi；

Si：貨物i的承重重量，i∈I；

CL：車廂的長度；

CW：車廂的寬度；

CH：車廂的高度；

CV：車廂的體積，CV=CL×CW×CH。

1.3　變量

連續決策變量：用于刻畫裝載方案的連續變量。

xi：貨物i的放置位置的x軸坐標，i∈I；

yi：貨物i的放置位置的y軸坐標，i∈I；

zi：貨物i的放置位置的z軸坐標，i∈I；

0-1決策變量：用于刻畫裝載方案的0-1變量。

αi：貨物i的裝載在車上則αi=1，否則，αi=0，i∈I；

βi：貨物i需要旋轉90°，如果貨物i長邊平行Y軸，寬邊平行X軸則βi=1，反之則βi=0；

0-1輔助決策變量：用于保證決策變量所刻畫的裝載方案為可行方案的變量。

lpij：貨物j在貨物i的X軸正方向上，則lpij=1，否則lpij=0；

wpij：貨物j在貨物i的Y軸正方向上，則wpij=1，否則wpij=0；

hpij：貨物j在貨物i的Z軸正方向上，則hpij=1，否則hpij=0。

1.4　目標函數

該問題的求解目標為車輛裝載率（裝入貨車的所有貨物體積之和／貨車車廂體積*100%）最大，即如式（1）所示：

（2）貨物互不嵌入約束。

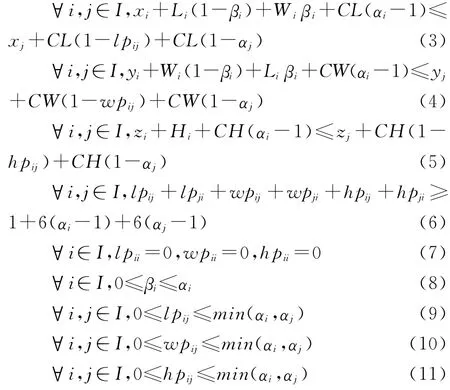
（3）貨物與車廂不相嵌約束，即如式（12-14）所示：

1.5　約束條件

一般三維裝載問題約束。一般三維裝載問題的約束主要有體積約束、裝入貨物互不嵌入約束和貨物與車廂不相嵌約束，具體約束的數學表達如下：

（1）體積約束：裝入所有貨物的體積總和不超過車廂最大容積，即如式（2）所示：

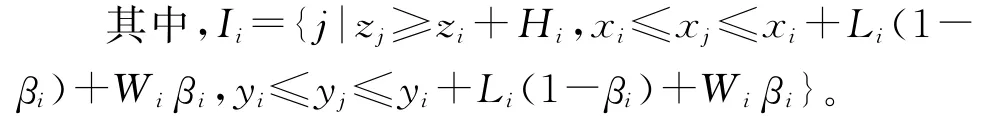
（3）堆疊約束：零部件包裝箱有多種類型，存在不同堆疊限制：①不允許堆疊；②僅允許同類型、同尺寸堆疊；③允許同類型，同尺寸／底面尺寸小的堆疊；④允許不同類型、同尺寸按既定順序堆疊；⑤允許不同類型，同尺寸／底面尺寸小的堆疊（本條約束過于繁瑣，本文中省略其數學模型表述）。

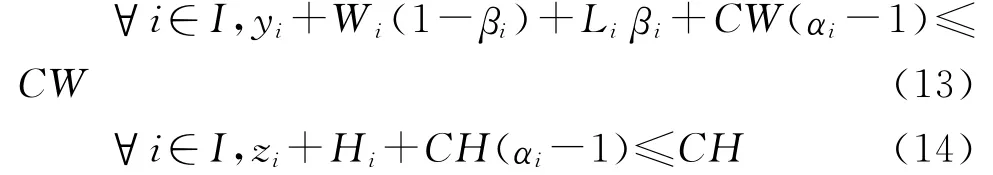
汽車零部件裝載中特殊約束。汽車零部件裝載問題中的特殊約束主要有完全支撐約束、單箱承重約束和貨物堆疊約束，具體數學表達如下：

（1）完全支撐約束：貨物必須得到車廂底部或其他一件貨物的完全支撐，不允許懸空。

（2）單箱承重約束：貨物疊放時，貨物重量不得大于支撐其擺放的貨物的承重能力。

2　基于裝載塊序列的混合模擬退火算法

由于汽車零部件三維裝載問題較經典三維裝箱問題在貨物堆疊方面更為復雜，現存的求解經典三維裝箱問題的算法很難直接應用到汽車零部件三維裝載問題上。因此，本文設計了一種基于裝載塊裝入順序的模擬退火算法。首先，將單箱貨物構造成為裝載塊（裝載塊不能在高度上堆疊），將三維裝載問題降為二維裝載問題。然后，利用模擬退火過程，將各裝載塊裝入車廂。該算法以裝載塊的裝載順序作為編碼方式，通過模擬退火過程隨機調整裝載序列以優化裝載序列對應的裝載方案，最后輸出算法結束時產生的裝載序列對應的裝載方案。以下算法流程中的集合、參數和變量的定義沿用上一小節中定義。

2.1　整體算法框架

基于裝載塊序列的混合模擬退火算法流程如下：

基于裝載塊序列的混合模擬退火算法

輸入：2.1中的待裝貨物集合；2.2中所有參數；降溫速度η，0＜η＜1；最大迭代次數n；降溫目

息βi，裝載率

否則，回到Step 4。

2.2　裝載塊生成子算法

裝載塊生成子算法輸入：2.1中的待裝貨物集合；2.2中所有參數。輸出：裝載塊序列B_list；貨物與裝載塊的對應關系。

Step 1：輸入2.1中的待裝貨物集合；2.2中所有參數。

Step 2：按照底面積從大到小順序將待裝貨物排序，生成待裝貨物列表I_list；初始化iI=1，iB=1。

Step 3：將I_list中第iI個貨物放置于裝載塊iB，并I_list=I_list＼｛iI｝。

Step 4：選擇I_list中滿足堆疊、承重等約束條件可堆疊于裝載塊iB的貨物中，底面積最大的貨物jI。

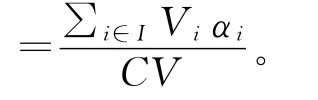
Step 1：輸入2.1中的待裝貨物集合和2.2中的所有參數；設置降溫速度η，0＜η＜1；最大迭代次數n；降溫目標tgoal。

Step 2：調用裝載塊生成子算法，生成裝載塊集合B。

Step 3：根據B隨機生成裝載塊的一個排序B_list（裝載序列）；設置初始溫度t＞tgoal。

Step 4：設置k=1。

Step 5：調用裝載方案生成子算法，計算適應度值F=f（B_list）。

Step 6：調用隨機擾動產生新的裝載序列B′_list；調用裝載方案生成子算法，計算適應度值F′=f（B′_list）。

Step 7：判斷適應度值是否改進，若F′＞F，則接受新的裝載序列B_list=B′_list；否則按照Metropolis概率準則接受新的裝載序列；令k=k+1。

Step 8：判斷是否k＞n，若是則執行Step 9；否則回到Step 5。

Step 9：冷卻退火，令t=t·η。

Step 10：判斷是否t＜tgoal，若是則調用裝載方案生成子算法，由B_list生成并輸出裝載方案，即對任意i∈I，放置位置的x軸坐標xi，y軸坐標yi，z軸坐標zi，是否裝載在車上αi，是否需要旋轉90°信標tgoal。

輸出：裝載方案，即對任意i∈I，放置位置的x軸坐標xi；y軸坐標yi；z軸坐標zi；是否裝載在車上αi；是否需要旋轉90°信息βi。裝載率f（B_list）

Step 5：若存在jI，則將jI放置于裝載塊iB目前已存在貨物的上一層，并I_list=I_list＼｛jI｝，回到Step 4。若不存在jI，則進入Step 6。

Step 6：判斷I_list是否為空，若是，則輸出結果；若不是，iB=iB+1，回到Step 3。

由此生成的裝載塊，塊與塊之間在高度方向（z軸方向）上不能相互疊放。

2.3　裝載方案生成子算法

為方便表達，這里做如下定義：

定義1（格局）設某一時刻，車廂內已放入若干裝載塊，還有若干個裝載塊待放，這稱為一個格局。車廂內尚未放入任何裝載塊時，稱為初始格局。所有裝載塊已放入車廂，或車廂外剩余的裝載塊無法再放入時，稱為終止格局。

定義2（可裝載點）可裝載點定義參考文獻［3］，可裝載點是在當前裝載格局下車廂中裝載塊的可行放置點。如圖2-（a）所示，初始可裝載點即為原點，坐標為（0，0），當裝入長為l寬為w的裝載塊后，可裝載點更新為（1，0）、（0，w）。如圖2-（b）所示，在某個裝載格局下，裝入3個裝載塊，當4號裝載塊裝入時，新增兩個可裝載點。

定義3（可裝載度）：可裝載度表示待裝載塊與可裝載點的匹配程度，用于指導每個裝載動作中可裝載點的選擇對任意裝載塊i在給定方向下和可裝載點j之間的可裝載度定義為一個向量當按給定方向可裝載點j裝不下目標待裝載塊i時，令Wkij=-1＜0，k∈｛1，2，3，4｝。反之，向量中各元素計算方法如下：

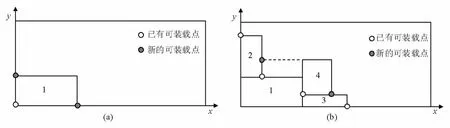
圖2　可裝載點示意圖

W1ij：新生成可裝載點指標。表示放入車廂后新生成的可裝載點數量，NE∈｛0，1，2｝，NE越小，表示箱子與當前空間的緊密度越高，因此，定義：

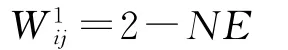
W2ij：穴度。具體定義參考文獻［4］，Bl，Bw表示裝入裝載塊的長和寬，Bd表示裝入裝載塊與車廂邊界或相鄰裝載塊最小距離，定義：

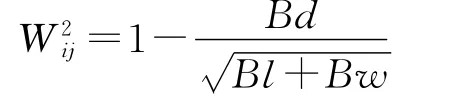
W3ij：封閉空間面積指標。封閉空間是指裝箱過程中，由裝載塊間或裝載塊與車廂四個邊界圍成的空白區域，面積為BA。封閉空間面積越大，說明裝載空間浪費越嚴重，因此定義封閉空間面積指標W3ij：

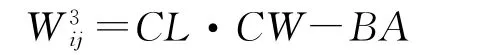
貼邊數。表示新裝入裝載塊與已裝入裝載塊或車廂邊界相貼的邊數

對任意裝載塊i和可裝載點我們記Wij大于裝載度如果；或和和或和裝載方案生成子算法的流程如下：

裝載方案生成子算法

輸入：裝載塊序列B_list；貨物與裝載塊的對應關系。

輸出：裝載方案，即對任意貨物i∈I，放置位置的x軸坐標xi；y軸坐標yi；z軸坐標zi；是否裝載在車上αi；是否需要旋轉90°信息βi。適應度值，即裝載率f（B_list）。

Step 1：輸入裝載塊序列B_list；貨物與裝載塊的對應關系，設置iB=1。

Step 2：選擇B_list中第iB個裝載塊；獲得當前格局下的可裝載點列表EP；計算B_list中第iB個裝載塊對EP中各可裝載點橫放／豎放的可裝載度值；第iB個裝載塊對EP中各可裝載點橫放／豎放的可裝載度值均小于0，則進入Step 4；否則，選擇可裝載點列表EP中可裝載度值最大的可裝載點和其對應的裝載方向作為第iB個裝載塊的裝載位置和裝載方向，進入Step 3。

Step 3：按照當前裝入裝載塊，得到一個新的格局。

Step 4：iB=iB+1。

Step 5：如果iB＞length（B_list），則算法終止，輸出裝載方案，即對任意貨物i∈I，放置位置的x軸坐標xi；y軸坐標yi；z軸坐標zi；是否裝載在車上αi；是否需要旋轉90°信息βi。裝載率f（B_list）=否則，回到Step 2。

2.4　隨機擾動

采用隨機置換的方式對裝載序列進行調整，即在裝載序列中隨機選擇兩個裝載塊位置進行交換，其他裝載塊排序不變。如初始裝載序列為［A，B，C，D，E，F，G］，隨機選擇到第1位和第5位進行交換，則新的裝載序列為［E，B，C，D，A，F，G］。

2.5　Metropolis準則

本文求解目標為裝載率最大，設置評價函數為裝載率F，若ΔF=F′-F≥0，則接受新的裝載序列，若ΔF＜0，則采用Metropolis準則，生成一個（0，1）之間的隨機數θ，若θ小于接受概率exp（10*ΔF／t），則同樣接受新的裝載序列，否則保留當前裝載序列。

3　算例分析

本文選取上海某汽車物流企業的零部件入廠物流三維裝載的實際運營數據，將算法優化裝載方案與實際運作中人工編排裝載方案進行比較，驗證算法能否有效處理零部件三維裝載問題，提高作業效率。

3.1　單箱裝載

（1）算例數據

如表1所示，共有8類159箱待裝零部件，數據包含貨物編號、長、寬、高、需求箱數等，采用9.6M貨車裝載，車廂長寬高分別為9400cm，2300cm，2300cm。

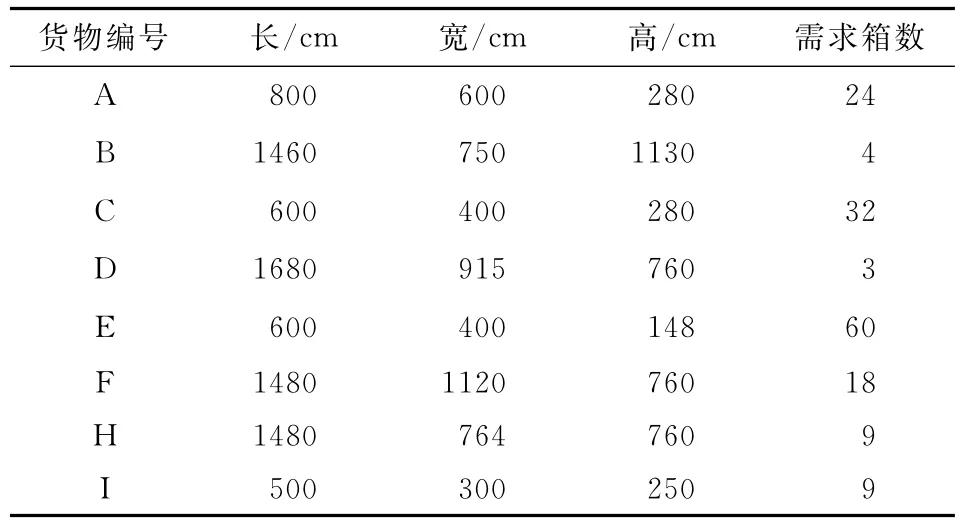
表1　單箱裝載數據

（2）算例結果

如表2所示，待裝零部件全部裝入車廂，裝載率達93.9%，裝載方案給出了零部件裝入順序、擺放方向及對應的坐標值，裝載效果如圖3表示。

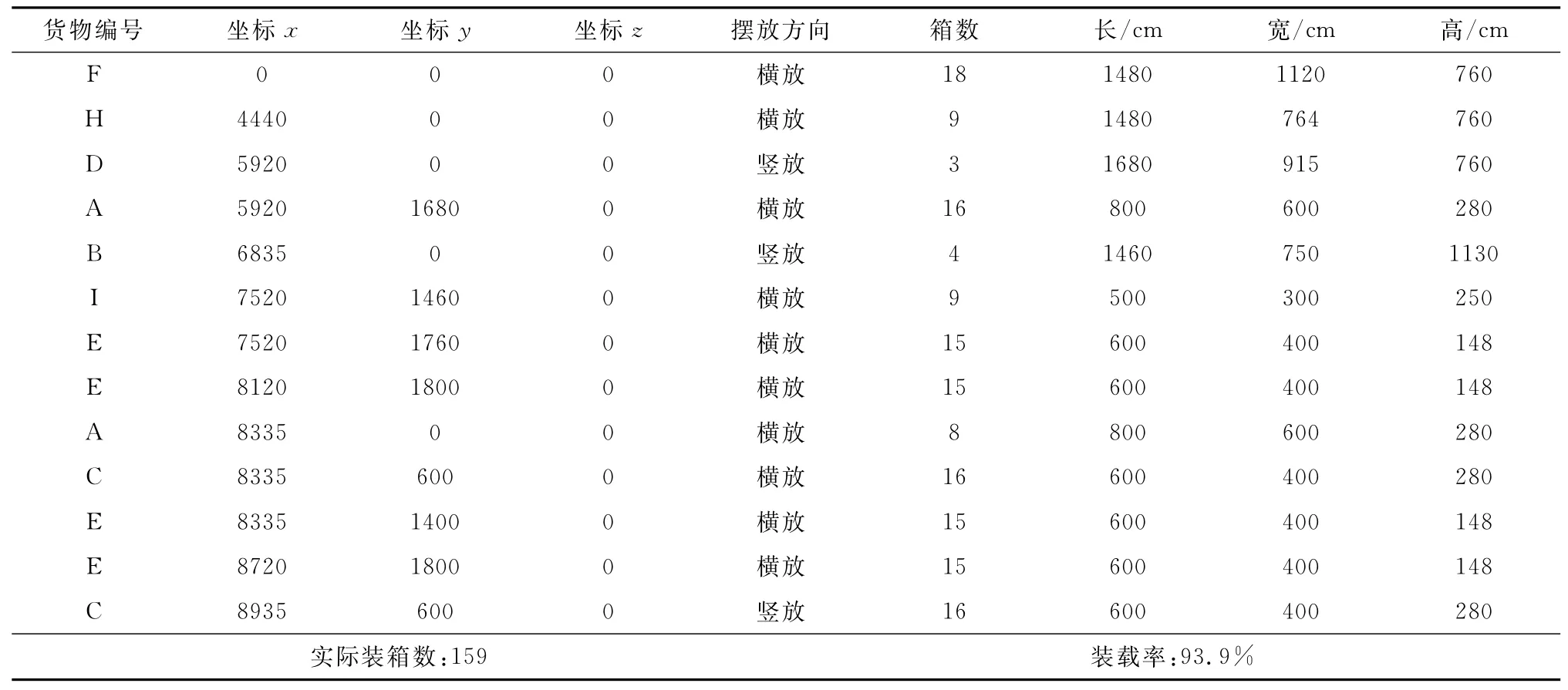
表2　單箱裝載結果

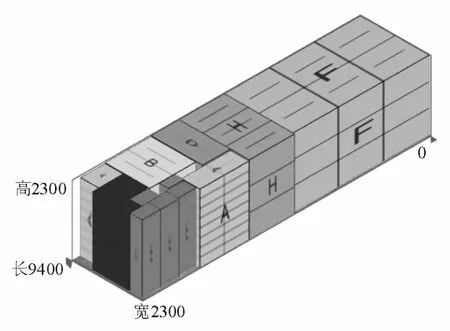
圖3　單箱裝載結果（單位：cm）

3.2　多箱裝載-單日數據對比

為了進一步驗證算法的有效性，選取該汽車物流企業一條取貨路線某天的全部裝箱需求數據，采用串行裝箱方式即裝滿一車廂再裝下一車廂，直至裝完全部待裝貨物，比較裝載率及車輛使用數等指標。

（1）算例數據：

共有31類1942箱待裝零部件，限于篇幅未列出具體數據。采用12M貨車裝載，車廂長寬高分別為11800cm，2300cm和2300cm。

（2）算例結果：

如表3所示，算法平均裝載率76.2%，需要使用10輛車；而實際運營中人工作業結果為安排了12輛車，平均裝載率為63.5%。

表3　20170503裝載算例結果

3.3　多箱裝載——10日數據對比

選取該路線連續10日裝箱數據，共有16950箱待裝零部件，限于篇幅未列出具體數據，僅列出每天待裝零部件類型、需求箱數、算法結果、人工結果以及優化效果，如表4所示。

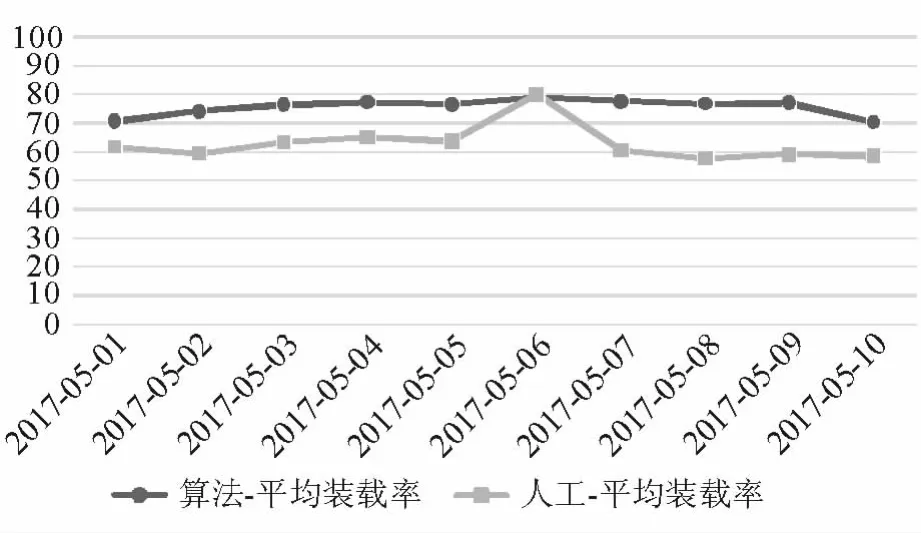
圖4　裝載率對比

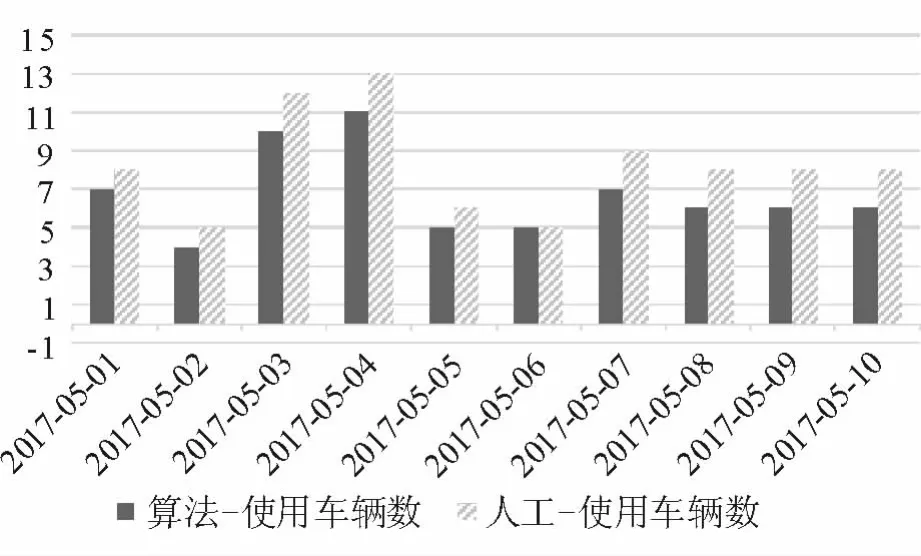
圖5　車輛使用數對比

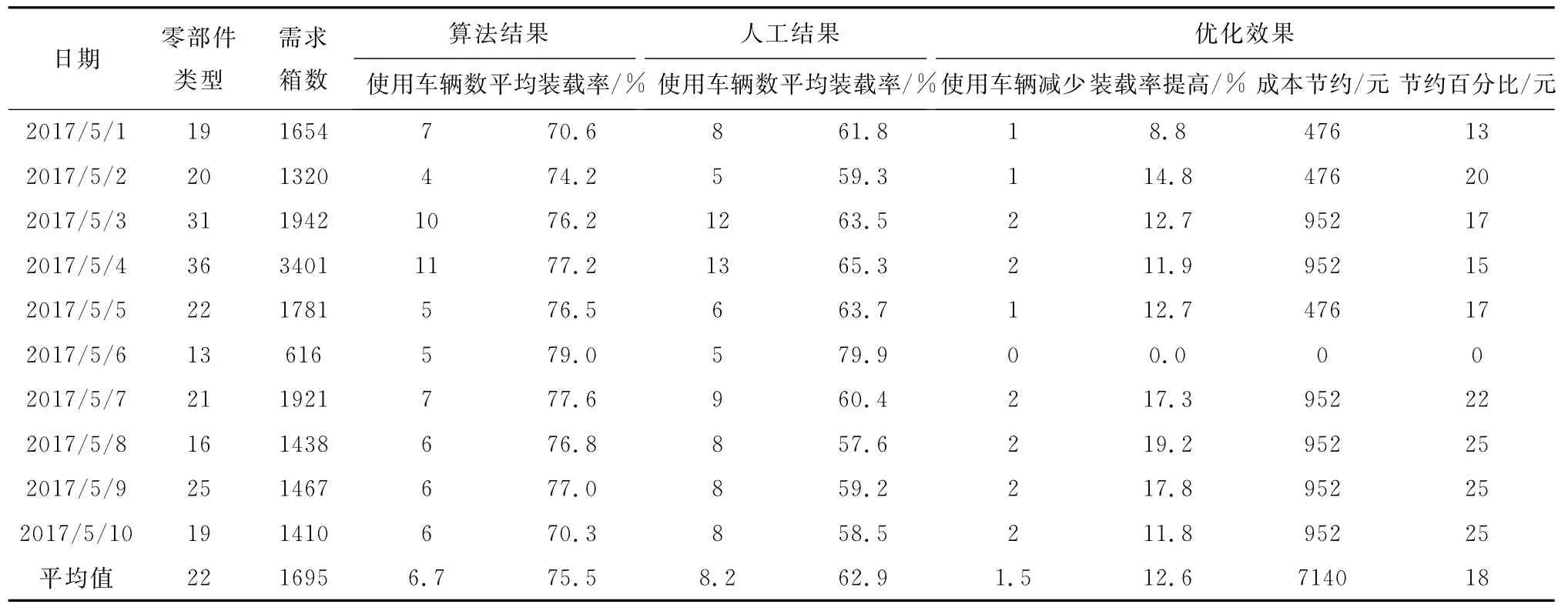
表4　連續10日裝載結果比較

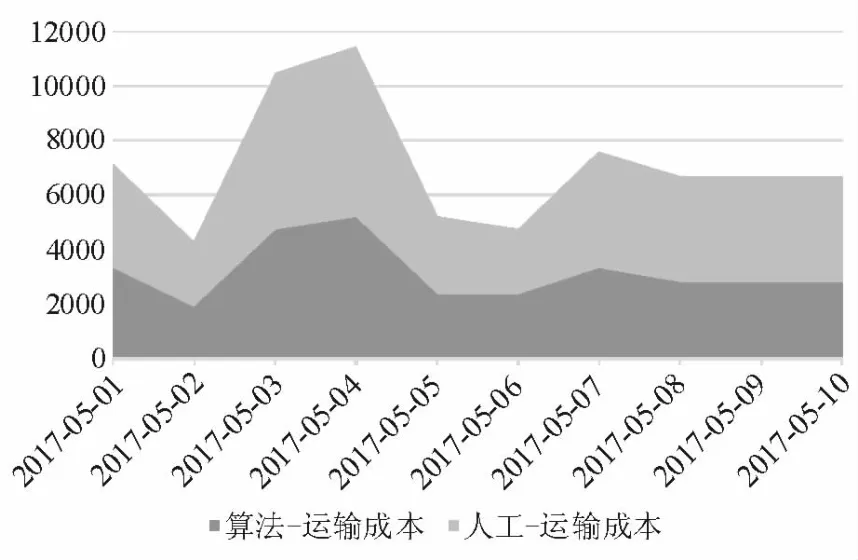
圖6　運輸成本對比

結果表明，本文算法能有效解決汽車零部件三維裝載問題，在車輛裝載率、車輛使用數等方面均優于人工編排結果。算法優化后平均使用車輛數為6.7輛，平均裝載率75.5%，實際運營使用車輛數8.2輛，平均裝載率62.9%。相比于人工結果，算法優化后平均車輛使用數減少1.5輛，平均裝載率提升12.6%。

從成本角度而言，優化后車輛使用數減少，直接降低了運輸成本、裝卸成本及人力成本等。以運輸成本為例，該取貨路線平均運輸距離為140公里，運輸費用為3.4元／公里，優化后10日運輸成本減少了7140元，較人工結果降低18%。

4　總結

本文針對汽車零部件入廠物流實踐中的零部件三維裝載問題，考慮汽車零部件堆疊規則、單箱承重等現實約束，設計了基于裝載塊裝載序列的混合模擬退火算法。通過使用上海某汽車物流企業的實際數據進行仿真實驗，并與人工操作方案進行對比，驗證了本文提出的算法能有效解決汽車零部件三維裝載問題。未來的研究方向為取貨路徑與裝載的協同優化問題。

參考文獻：

［1］ BOYSEN N，EMDE S，HOECK M，et al.Part logistics in the automotive industry：decision problems，literature review and research agenda［J］.European Journal of Operational Research，2015，242（1）：107-120.

［2］ 何明珂，張屹然.國內汽車零件入廠物流研究綜述［J］.中國流通經濟，2011，25（7）：31-36.

［3］ CRAINIC T G，PERBOLI G，TADEI R.Extreme point-based heuristics for three-dimensional bin packing［J］.Informs Journal on Computing，2008，20（3）：368-384.

［4］ 何琨，黃文奇，金燕.基于動作空間求解二維矩形Packing問題的高效算法［J］.軟件學報，2012，34（5）：1037-1044.

［5］ 何琨，黃文奇.基于動作空間的三維裝箱問題的確定性高效率求解算法［J］.計算機學報，2014，37（8）：1786-1793.

［6］ PARRENO F，ALVAREZ-VALDES R，OLIVEIRA J F，et al.Neighborhood structures for the container loading problem：a VNS implementation［J］.Journal of Heuristics，2010，16（1）：1-22.

［7］ FANSLAU T，BORTFELDT A.A tree search algorithm for solving the container loading problem［J］.Informs Journal on Computing，2010，22 （2）：222-235.

［8］ 張德富，彭煜，朱文興，等.求解三維裝箱問題的混合模擬退火算法［J］.計算機學報，2009，32（11）：2147-2156.

［9］ 張德富，彭煜，張麗麗.求解三維裝箱問題的多層啟發式搜索算法［J］.計算機學報，2012，35（12）：2553-2561.

［10］ 劉勝，朱鳳華，呂宜生，等.求解三維裝箱問題的啟發式正交二叉樹搜索算法［J］.計算機學報，2015，38（8）：1530-1543.

［11］ 靳志宏，蘭輝，郭貝貝.基于現實約束的集裝箱裝箱優化及可視化［J］.系統工程理論與實踐，2010，30（9）：1722-1728.

［12］ 張瑩，劉二超，戚銘堯.考慮支撐面約束的三維裝箱問題快速求解方法［J］.交通運輸系統工程與信息，2014，14（2）：192-198.

［13］ 那日薩，崔雪蓮，韓琪瑋，等.有角件約束的集裝箱裝箱問題優化算法［J］.工業工程與管理，2016，21（1）：1-7.