基于新課程背景下初中生幾何直觀能力的培養

王 祎

（北京市上地實驗學校）

幾何直觀能力就是根據當前所看到的東西進行思考、分析、總結。簡單來講，幾何直觀就是將復雜的數學問題通過圖形方式簡單化，并通過對圖形進行科學分析，發現問題的實質，培養學生的邏輯分析能力。那么，基于新課改背景下，如何提升初中學生的幾何直觀能力？我認為需要從以下幾方面研究。

一、利用數形結合方式提升學生的幾何直觀能力

華羅庚曾經說過：“數缺形時少直觀，形少數時難入微，數形結合百般好，隔離分家萬事休。”由此可見，數和形是數學教學中非常重要組成部分，要想更好地了解數學，學懂數學，就離不開與圖形的結合。所以，在對學生幾何直觀能力培養過程中，應該特別注重對圖形語言的分析，讓學生學會在答題過程中運用圖形來進行解答，將代數問題與幾何問題巧妙結合起來，充分將幾何直觀能力貫徹到代數的學習過程中。

這道題從題目上來看比較復雜，僅僅是已知正實數X，學生往往不知道如何下手，這個時候，我們不妨換個思路來思考，采用數形結合的方式進行解答。

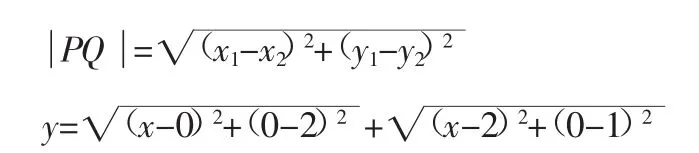
用對稱軸求最短距離的方式來進行計算，通過對圖形的分析和利用，問題迎刃而解。

二、通過對知識點大膽設疑提升學生的幾何直觀能力

在數學教學過程中，確保學生能夠正確掌握、運用基礎知識，大膽對問題假設，進行合理設疑，從而強化學生的創造性思維能力。例如在進行下列題目解答過程中，就可以充分運用設疑求證的思維模式進行問題解答。

如圖所示，在△ABC中，∠BAC的平分線與∠ABC的平分線相較于E點，D為AE延長線與△ABC外接圓的交點，連接CE、CD、BD，已知∠CDB=120°，∠CDA=60°。試分析四邊形BECD的形狀。

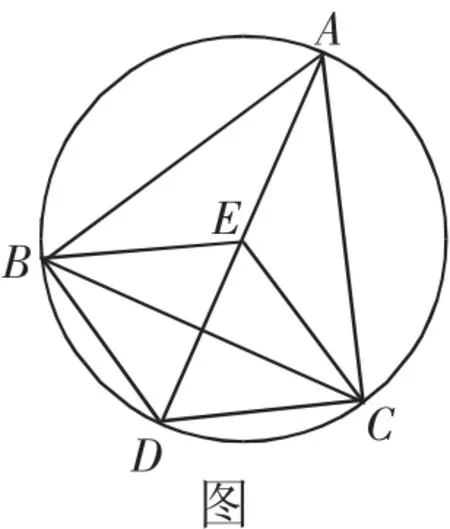
通過肉眼觀察圖1，我們可以假設四邊形BECD為菱形，如何證明這一假設，就需要從菱形的定義出發，證明四邊形BECD的其中一組相鄰邊平行或者是四邊都相等。

解答：因為∠CDB=120°，∠CDA=60°，根據圓周角定理可知半圓角CAB和CDB分別為240°和120°。因為四邊形ACDB為圓的內接四邊形，又因為∠CDB=120°，所以∠CAB=60°。因為AD為∠CAB的角平分線，所以，∠CAD=∠BAD=30°，半圓角BD=CD，所以BD=CD，又因為∠DCB=∠CAD=30°，BE是∠CBA的角平分線，所以，∠DBE=60°。同理可證∠DCE=60°。根據兩組對角分別相等的四邊形是平行四邊形，可判定四邊形BECD為平行四邊形，又因為BD=CD，所以四邊形BECD為菱形。

通過這種大膽設疑的方式，從方向思維來提出例證，培養學生的幾何直觀能力；利用基礎知識大膽假設，小心求證的過程，有利于培養學生嚴謹的數學探索精神。

三、巧妙利用多媒體技術提升學生的幾何直觀能力

隨著科技的不斷創新，多媒體技術已經被廣泛運用于教育領域，因此，在初中數學課堂教學中，教師可以巧妙利用多媒體技術，結合多媒體直觀、形象、圖文并茂的特點，制作具有直觀性的教學課件，將枯燥抽象的數學知識形象生動化，拓展學生的思維創作能力，開拓學生視野，從而激發學生的學習興趣，通過自主學習方式，不斷培養自己的幾何直觀能力。但是值得我們教育工作者注意的是，多媒體技術僅僅是一種輔助的教學方式，教師不能完全依賴它，教學工作終究還是要回歸課本內容。

總而言之，初中生正處于智力高速發展的重要階段，雖然對于幾何知識的學習才剛剛起步，但是，初中生的理解認知能力也正處于特別敏感的時期，因此教師在日常的教學活動中要采取有效的方法來培養學生的幾何直觀能力，使學生形成良好的圖形感知能力。當然，這需要我們教育工作者在實踐工作中不斷探索，促進學生幾何直觀能力的有效發展。

參考文獻：

魏珂，胡典順.從一道幾何題的求解淺談幾何直觀能力的培養［J］.中國數學教育，2017（Z3）:44-46.