基于進(jìn)化粒子濾波的數(shù)據(jù)域直接跟蹤方法

逯志宇, 巴 斌, 任衍青, 王大鳴

(信息工程大學(xué)信息系統(tǒng)工程學(xué)院, 河南 鄭州 450001)

0 引 言

目標(biāo)跟蹤是對(duì)目標(biāo)位置和速度的實(shí)時(shí)估計(jì),無論是在民用領(lǐng)域還是軍事領(lǐng)域,都是不可或缺的重要技術(shù)。尤其隨著航空航天事業(yè)的蓬勃發(fā)展,以及現(xiàn)代戰(zhàn)爭(zhēng)信息化的轉(zhuǎn)變,運(yùn)動(dòng)目標(biāo)位置與速度的實(shí)時(shí)估計(jì)和預(yù)測(cè)具有重要研究?jī)r(jià)值,已成為一個(gè)十分活躍的研究方向[1]。

傳統(tǒng)跟蹤方法首先利用接收信號(hào)估計(jì)含有目標(biāo)位置信息的到達(dá)時(shí)間(time of arrival, TOA)[2]、到達(dá)角度(angle of arrival, AOA)[3]、到達(dá)時(shí)間差(time difference of arrival, TDOA)[4]或到達(dá)頻率差(frequency difference of arrival, FDOA)[5]等位置參數(shù),然后通過求解這些參數(shù)構(gòu)成的跟蹤方程獲得目標(biāo)運(yùn)動(dòng)軌跡。由于跟蹤方程非線性較強(qiáng),在目標(biāo)位置和速度的聯(lián)合估計(jì)中面臨高維搜索問題,為此文獻(xiàn)[6]提出了一種加權(quán)兩步最小二乘算法對(duì)定位方程進(jìn)行求解,然后利用卡爾曼濾波(Kalman filtering, KF)方法對(duì)估計(jì)結(jié)果進(jìn)行平滑得到運(yùn)動(dòng)軌跡。雖然這種方法簡(jiǎn)單易于實(shí)現(xiàn),但是在低信噪比條件下性能惡化嚴(yán)重,跟蹤效果不佳。為了解決此問題,擴(kuò)展卡爾曼濾波(extended KF, EKF)被引入到跟蹤系統(tǒng)中[7],不需要求解跟蹤方程,而是根據(jù)位置參數(shù)對(duì)目標(biāo)運(yùn)動(dòng)狀態(tài)進(jìn)行實(shí)時(shí)估計(jì),相對(duì)KF方法具有更好的性能。但是,EKF算法利用泰勒級(jí)數(shù)展開近似非線性函數(shù),并且只保留了一階項(xiàng),在低信噪比下會(huì)帶來較大誤差,甚至濾波發(fā)散[8]。針對(duì)EKF算法的缺點(diǎn),很多改進(jìn)算法被提出,如無損卡爾曼濾波(unscented Kalman filter, UKF)[9]、積分卡爾曼濾波(quadrature Kalman filter, QKF)[10]、容積卡爾曼濾波(cubature Kalman filtering, CKF)[11]、粒子濾波(particle filter, PF)[12]等,這些算法在非線性函數(shù)擬合上能夠達(dá)到更高階的近似,跟蹤性能不斷提升。

雖然經(jīng)過算法改進(jìn),傳統(tǒng)兩步跟蹤算法的精度不斷提高,但這種跟蹤方法在本質(zhì)上仍然存在兩點(diǎn)不足:一是在參數(shù)估計(jì)階段忽略了觀測(cè)站之間的聯(lián)系,各觀測(cè)站之間參數(shù)估計(jì)過程相互獨(dú)立,并未考慮定位參數(shù)來自于同一目標(biāo)這一先驗(yàn)信息,損失了部分位置信息;二是第一步參數(shù)估計(jì)將引入處理誤差,誤差的傳遞和累積不可避免,導(dǎo)致第二步跟蹤精度受限。因此兩步方法是次優(yōu)的,不能獲得最佳的估計(jì)精度[13]。與之相比,近些年被提出的直接定位(direct position determination, DPD)算法不需要參數(shù)估計(jì)和位置解算分步計(jì)算,而是基于采樣信號(hào)直接估計(jì)目標(biāo)位置,避免了兩步定位算法的缺點(diǎn),能夠獲得更好的定位效果,已得到廣泛的研究[14-19]。

文獻(xiàn)[20-21]首先詳細(xì)闡述了DPD算法的基本原理,并給出了利用角度和時(shí)延信息的最大似然估計(jì)方法。針對(duì)最大似然估計(jì)高復(fù)雜度問題,文獻(xiàn)[22]提出了子空間數(shù)據(jù)融合DPD算法,文獻(xiàn)[23-24]提出了最小方差無失真響應(yīng)(minimum variance distortionless response, MVDR)算法,均降低了參數(shù)估計(jì)維度,減輕了計(jì)算壓力。考慮觀測(cè)站運(yùn)動(dòng)場(chǎng)景,文獻(xiàn)[25]提出了異步觀測(cè)條件下的多運(yùn)動(dòng)站DPD算法,文獻(xiàn)[26]提出了基于時(shí)間和多普勒信息的DPD算法。將數(shù)據(jù)域直接位置解算思想引入到目標(biāo)跟蹤領(lǐng)域,以基于TOA[27]、TDOA[28]和FDOA[29]等信息的DPD算法為基礎(chǔ),文獻(xiàn)[30-31]提出了一種目標(biāo)直接跟蹤(direct trajectory determination, DTD)算法,給出了利用時(shí)延和多普勒頻率信息的算法原理,證明了DTD算法性能優(yōu)于傳統(tǒng)兩步跟蹤算法。然而上述文獻(xiàn)利用了離散時(shí)延和多普勒信息,引入量化誤差,在采樣率較低時(shí)嚴(yán)重影響跟蹤精度,性能仍有待進(jìn)一步提高。

綜上所述,為了進(jìn)一步提高目標(biāo)跟蹤性能,本文提出了一種利用連續(xù)時(shí)延和多普勒信息的直接跟蹤算法。與現(xiàn)有文獻(xiàn)相比,本文的貢獻(xiàn)在于,進(jìn)一步提高了目標(biāo)直接跟蹤精度,并利用進(jìn)化PF方法提高跟蹤收斂速度,使算法更具實(shí)用價(jià)值。同時(shí),本文還推導(dǎo)了所提跟蹤模型的克拉美羅下界(Cramer-Rao lower bound, CRLB),給出了基于直接數(shù)據(jù)域跟蹤的誤差界限。

1 數(shù)據(jù)域直接跟蹤模型

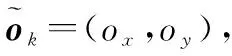
設(shè)xk為目標(biāo)發(fā)送的信號(hào),假設(shè)信號(hào)模型為

x(t)=s(t)ej2πfct

(1)

式中,fc是載頻;s(t)是信號(hào)的包絡(luò)。設(shè)采樣點(diǎn)數(shù)為Nk,第l個(gè)觀測(cè)站在第k次觀測(cè)時(shí)得到采樣信號(hào)為

nk=1,2,…,Nk

(2)

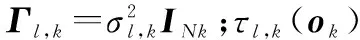
(3)

(4)

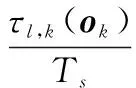
(5)

Bτl,k(ok)=diag{exp(-j2π/Nknkτl,k(ok)/Ts)}

(6)

令

Bvl,k(ok)=diag{exp(j2πTsvl,k(ok)nk)}

(7)

聯(lián)合式(5)～式(7),令

Hl,k(ok)=Bvl,k(ok)VHBτl,k(ok)V

(8)

Hl,k(ok)包含了目標(biāo)的位置和速度參數(shù),由于利用了時(shí)間和多普勒信息,稱之為時(shí)頻觀測(cè)矩陣。因此可將接收信號(hào)表示為

rl,k=Bvl,k(ok)VHBτl,k(ok)Vxk+wl,k=Hl,k(ok)xk+wl,k

(9)

令

(10)

則所有觀測(cè)站的接收信號(hào)聯(lián)合表示為

rk=Hk(ok)xk+wk

(11)

通過上述方法,使用連續(xù)時(shí)間信息避免了量化誤差的引入,將進(jìn)一步提升跟蹤性能。系統(tǒng)基于接收信號(hào)的狀態(tài)方程和觀測(cè)方程可以表示為

ok+1=Fok+σk

(12)

rk=H(ok)xk+wk

(13)

式中,F為狀態(tài)轉(zhuǎn)移矩陣;σk為零均值高斯白噪聲,表示目標(biāo)狀態(tài)的抖動(dòng)誤差,其協(xié)方差矩陣為

(14)

2 PF直接跟蹤算法

在兩步跟蹤算法中,時(shí)間和頻率等參數(shù)作為觀測(cè)量,可采用的濾波方法較多,如EKF、UKF、CKF、PF等,并且在高信噪比條件下,性能相差并不明顯。但是在直接跟蹤方法中,由于觀測(cè)量是接收信號(hào),非線性更強(qiáng),導(dǎo)致EKF、UKF等方法效果并不理想,所以在直接跟蹤中選擇能夠處理更強(qiáng)非線性問題的PF算法較為合理。

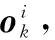
(15)

根據(jù)大數(shù)定理,當(dāng)M足夠大時(shí),p(ok|rk)將收斂于真實(shí)的后驗(yàn)概率。粒子權(quán)重計(jì)算公式為

(16)

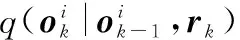
(17)

(18)

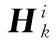
(19)

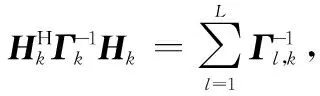
(20)

根據(jù)式(11),利用最小二乘準(zhǔn)則,xk可表示為

(21)

將式(21)代入式(20),可以得到

(22)

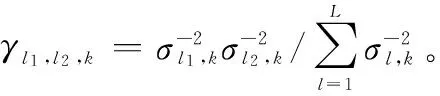
(23)

從而得到估計(jì)結(jié)果為

(24)

根據(jù)式(17),下一時(shí)刻的采樣粒子為

(25)

為了解決PF存在的退化和貧化問題,基于遺傳進(jìn)化思想的粒子空間構(gòu)造(evolutionary particle filter, EPF)方法較為常用,即對(duì)某些粒子進(jìn)行變異來增加粒子的多樣性,然后根據(jù)一定的準(zhǔn)則選擇出優(yōu)質(zhì)粒子進(jìn)行下一代的計(jì)算。下面給出一種進(jìn)化策略,由變異操作和選擇方法組成。在每一代濾波過程中,根據(jù)式(25)產(chǎn)生的新粒子,利用式(26)進(jìn)行如下操作。

(26)

基于數(shù)據(jù)域的運(yùn)動(dòng)目標(biāo)直接跟蹤算法相比于兩步跟蹤算法精度得到了提升。針對(duì)其高度非線性特點(diǎn),本節(jié)給出了利用進(jìn)化PF的迭代求解算法,與文獻(xiàn)[31]所用的標(biāo)準(zhǔn)PF相比,目標(biāo)跟蹤效率得到提升,仿真實(shí)驗(yàn)中將進(jìn)一步證明所提算法的有效性。結(jié)合上述原理分析,可以將基于EPF的直接跟蹤(EPF-DTD)算法概括如下:

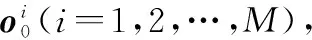
步驟2根據(jù)式(26)對(duì)采樣粒子進(jìn)行變異操作,得到新的粒子集;

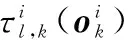
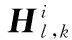
步驟5根據(jù)權(quán)重大小對(duì)粒子進(jìn)行篩選,選擇權(quán)重較大的一半作為優(yōu)質(zhì)粒子;

步驟6利用優(yōu)質(zhì)粒子,根據(jù)式(24)得到本次迭代的目標(biāo)狀態(tài)估計(jì);

步驟7利用輪盤賭方法對(duì)粒子進(jìn)行重采樣,根據(jù)式(25)得到下一代粒子;

步驟8如果迭代終止,將本次結(jié)果作為輸出,否則跳轉(zhuǎn)步驟2進(jìn)行下一次迭代。

3 CRLB

CRLB給出了無偏估計(jì)量的方差下限,對(duì)研究模型的理論性能具有重要意義。本節(jié)將推導(dǎo)一種所提直接跟蹤模型CRLB的遞歸求解算法,給出目標(biāo)狀態(tài)的估計(jì)性能界限。

設(shè)P(r,o)是(r,o)聯(lián)合概率分布,則費(fèi)希爾信息矩陣(Fisher information matrix, FIM)可以表示為

(27)

式中,Δ為偏導(dǎo)算子,表示為

(28)

(29)

則o2的FIM矩陣可以表示為

(30)

式中,J2也稱為o2的信息子矩陣。

Pk+1=PkP(rk+1|ok+1)P(ok+1|ok)

(31)

從而k時(shí)刻的FIM矩陣可以表示為

(32)

進(jìn)一步,在k+1時(shí)刻可以得到

(33)

根據(jù)式(31),可以得到

lgPk+1=lgPk+lgP(rk+1|ok+1)+lgP(ok+1|ok)

(34)

所以式(33)可以表示為

(36)

令

(37)

顯然,有式(38)成立

(38)

從而有

(39)

根據(jù)式(30),第k+1時(shí)刻對(duì)新增ok+1的信息子矩陣為

(40)

化簡(jiǎn)可得

(41)

根據(jù)式(32)有

(42)

所以結(jié)合式(41)和式(42),可以得到CRLB的遞推公式為

(43)

結(jié)合第1節(jié)給出的跟蹤模型,式(37)可以表示為

(44)

式中

(45)

表示在k+1時(shí)刻狀態(tài)ok+1獨(dú)立的FIM矩陣,根據(jù)式(11)和式(27),有

(46)

利用鏈?zhǔn)椒▌t,可以得到

(47)

式中

(48)

(49)

(50)

(51)

4 仿真分析

為了驗(yàn)證所提算法的性能,本節(jié)將對(duì)EPF-DTD算法的跟蹤精度和CRLB進(jìn)行仿真,并與文獻(xiàn)[31]中提出的時(shí)延和多普勒信息離散化直接跟蹤算法(簡(jiǎn)記為PF-DTD)和基于時(shí)頻差的兩步跟蹤算法(簡(jiǎn)記為PF-TDOA/FDOA)進(jìn)行對(duì)比。

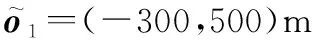
為了說明各算法的跟蹤性能,在信噪比20 dB條件下,得到算法的跟蹤效果如圖1所示,運(yùn)動(dòng)方向由下向上,跟蹤誤差變化曲線如圖2所示。可以看出,3種算法在經(jīng)過短暫的調(diào)整后都能以一定的誤差跟蹤目標(biāo),其中PF-DTD算法的跟蹤精度和速度比PF-TDOA/FDOA算法略有提升,證明直接跟蹤方法具有一定優(yōu)勢(shì)。但是由于PF-DTD算法對(duì)時(shí)延做了量化處理,引入了部分量化噪聲,直接跟蹤方法的性能優(yōu)勢(shì)并未完全展現(xiàn)。EPF-DTD算法避免了量化問題,并且對(duì)PF算法做了改進(jìn),所以在跟蹤速度和精度上相對(duì)于PF-DTD算法具有較大的提高。在圖1的放大圖中可以看到,當(dāng)目標(biāo)做折線運(yùn)動(dòng)時(shí),EPF-DTD能夠在短時(shí)間內(nèi)快速的跟蹤目標(biāo)運(yùn)動(dòng)變化,并且誤差能夠保持在較低水平,而PF-DTD和PF-TDOA/FDOA算法的跟蹤速度相對(duì)較慢,誤差變化較大,進(jìn)一步證明了本文所提算法的有效性。

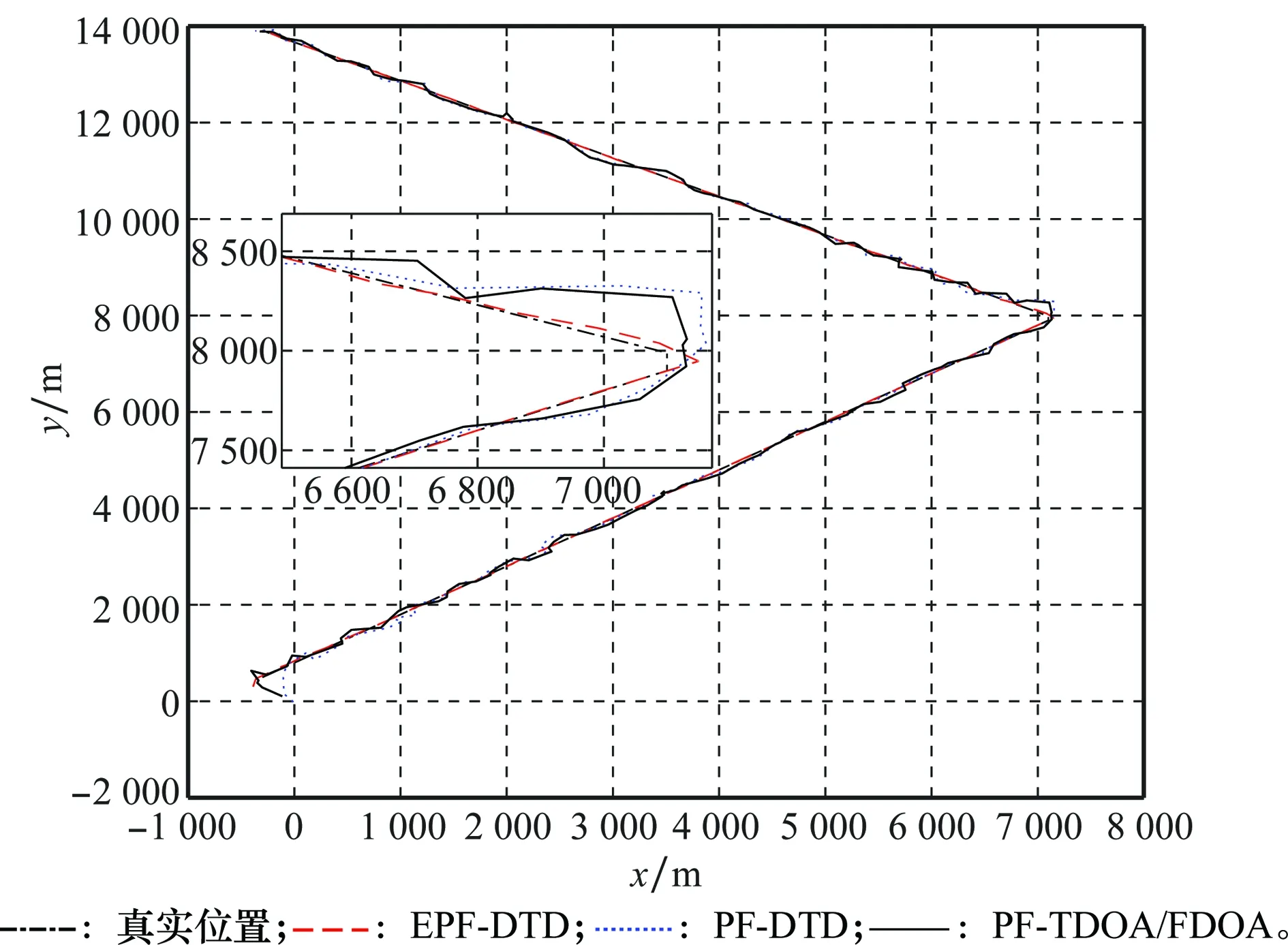
圖1 不同算法位置跟蹤過程Fig.1 Position tracking of different algorithms

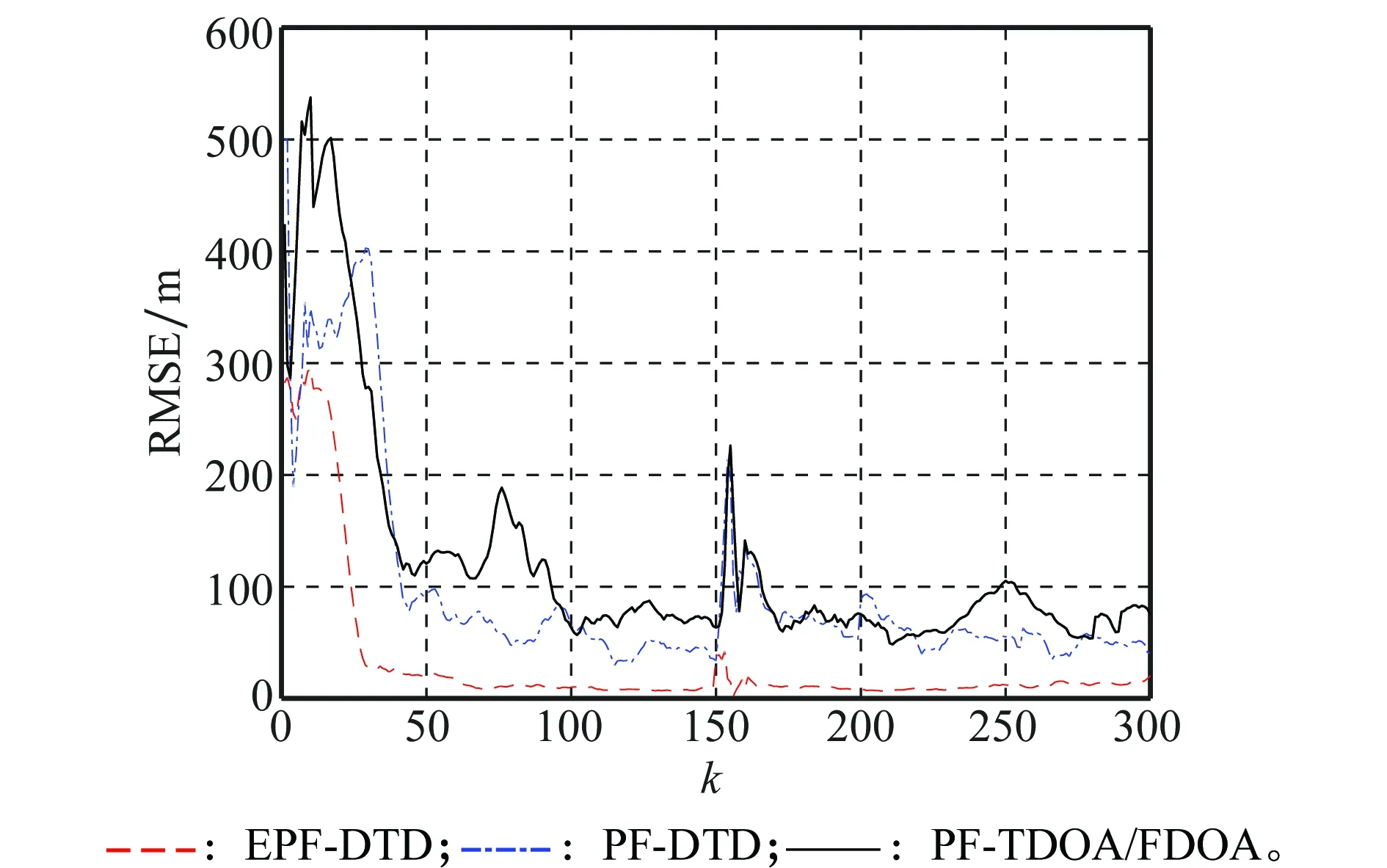
圖2 不同算法位置均方根誤差Fig.2 Root mean square error (RMSE) of location for different algorithms

在相同條件下,圖3和圖4是速度跟蹤效果以及誤差曲線。從圖中可以看出,PF-DTD和PF-TDOA/FDOA算法的速度跟蹤能力大致相同,且誤差較大,而EPF-DTD算法能夠在短時(shí)間內(nèi)達(dá)到較好的跟蹤效果,最終誤差能夠維持在較低水平。當(dāng)目標(biāo)做折線運(yùn)動(dòng)時(shí),EPF-DTD可以快速跟蹤目標(biāo)速度變化,而PF-DTD和PF-TDOA/FDOA算法的跟蹤效果相對(duì)較差。出現(xiàn)這種現(xiàn)象的原因是,速度的跟蹤能力取決于FDOA信息的處理能力,PF-TDOA/FDOA算法對(duì)FDOA參數(shù)的估計(jì)精度較低,影響了跟蹤精度,PF-DTD算法中的量化誤差也間接影響了速度的跟蹤效果,而EPF-DTD算法避免了上述問題,因此速度跟蹤效果較為理想。

為了說明EPF-DTD算法的跟蹤性能,得到其CRLB隨迭代次數(shù)k和信噪比的變化曲線如圖5所示。可以看出,隨著信噪比的增加,算法的跟蹤精度不斷提高,證明了算法的跟蹤性能。隨著迭代次數(shù)的增加,在高信噪比條件下,跟蹤精度相應(yīng)提高,并且能夠快速收斂；但是在較低信噪比條件下,收斂速度變慢,需要較長(zhǎng)時(shí)間才能夠穩(wěn)定。原因在于,一方面,觀測(cè)信號(hào)較弱時(shí),無法快速消除先驗(yàn)假設(shè)引進(jìn)的誤差；另一方面,由于目標(biāo)運(yùn)動(dòng),不同位置所能達(dá)到的理論估計(jì)精度會(huì)有波動(dòng),在信噪比較低時(shí)會(huì)對(duì)跟蹤性能帶來影響。

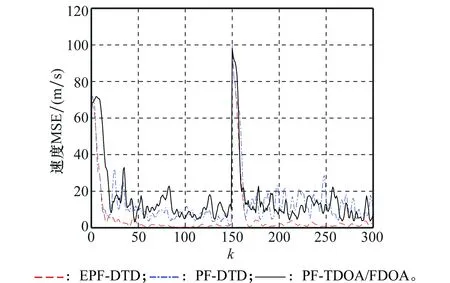
圖4 不同算法速度跟蹤誤差Fig.4 Speed tracking error of different algorithms

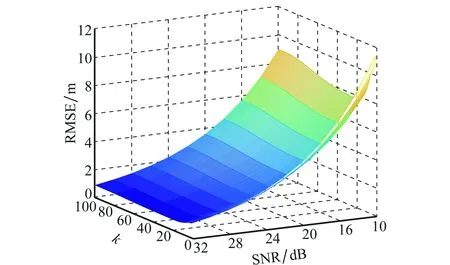
圖5 EPF-DTD算法的CRLB隨迭代次數(shù)k和信噪比的變化曲線Fig.5 CRLB of EPF-DTD algorithm over signal-to-noise ratio (SNR) and k

進(jìn)一步,令迭代次數(shù)k=100,對(duì)各算法進(jìn)行50次蒙特卡羅仿真實(shí)驗(yàn),將不同算法位置估計(jì)誤差隨信噪比的變化趨勢(shì)進(jìn)行對(duì)比,其結(jié)果如圖6所示。可以看出,PF-DTD算法與PF-TDOA/FDOA算法在高信噪比條件下性能相近,但在低信噪比條件下,PF-DTD算法性能有明顯提升,證明了直接跟蹤思想的正確性。相比于PF-DTD和PF-TDOA/FDOA算法,本文提出的EPF-DTD算法在跟蹤精度上有較大地提升,證明算法構(gòu)造連續(xù)時(shí)延信息模型以及利用EPF算法求解的有效性。同時(shí)可以看到,EPF-DTD算法能夠接近CRLB,由于實(shí)際濾波中粒子數(shù)量有限,與CRLB仍有微小距離,但在高信噪比條件與CRLB基本吻合。

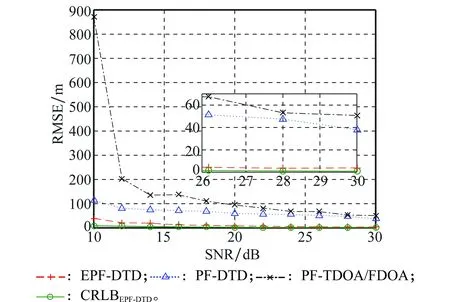
圖6 不同算法性能隨信噪比變化曲線Fig.6 RMSE of position versus SNR of different algorithms

為了驗(yàn)證不同采樣頻率對(duì)算法的影響,在fs=1 MHz和fs=0.5 MHz條件下對(duì)EPF-DTD算法和PF-DTD算法的跟蹤誤差進(jìn)行了仿真,結(jié)果如圖7所示。可以看出,采樣頻率對(duì)EPF-DTD算法的影響較小,不同采樣率下算法的跟蹤性能相近。而PF-DTD算法由于受量化誤差的影響,當(dāng)采樣頻率下降時(shí),性能下降較快。結(jié)果說明，本文所提EPF-DTD算法有效避免了PF-DTD算法的量化誤差問題,可以在較小采樣率下獲得優(yōu)異的跟蹤性能。

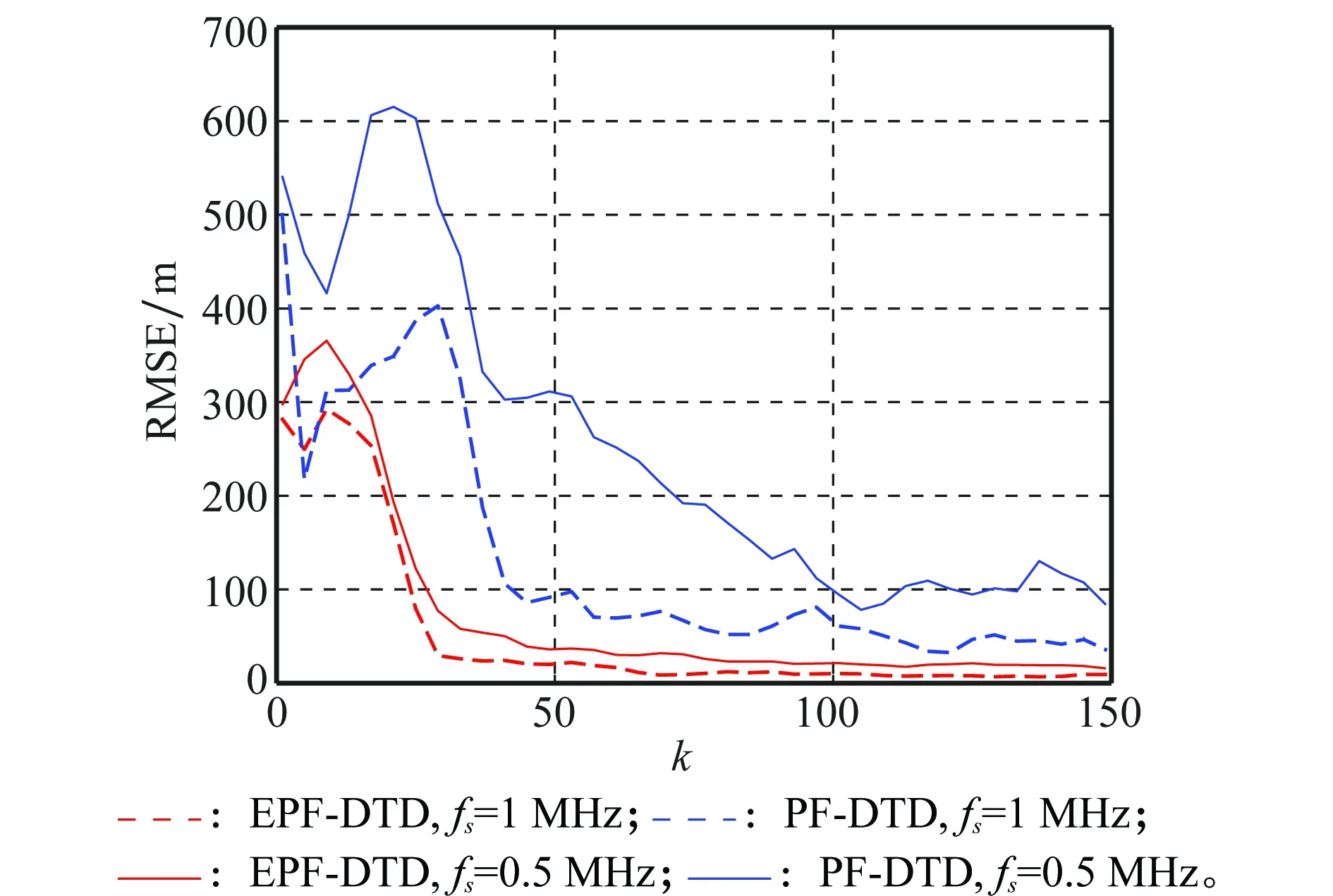
圖7 不同采樣頻率時(shí)算法跟蹤誤差對(duì)比Fig.7 Comparison of tracking error at different sampling rates

5 結(jié) 論

本文針對(duì)目標(biāo)跟蹤問題,提出一種利用連續(xù)時(shí)延信息,并基于進(jìn)化PF的直接跟蹤方法,給出了詳細(xì)的模型構(gòu)建、原理分析和CRLB推導(dǎo)過程。所提算法利用觀測(cè)站接收信號(hào)直接進(jìn)行目標(biāo)跟蹤,具有比兩步定位更高的跟蹤精度,同時(shí)進(jìn)化PF方法提高了算法的計(jì)算效率。仿真實(shí)驗(yàn)給出了所提算法與其他算法的性能對(duì)比,證明了算法能夠獲得更好的跟蹤性能,具有一定實(shí)用價(jià)值。

參考文獻(xiàn)：

[1] 楊峰,張婉瑩.一種多模型貝努利粒子濾波機(jī)動(dòng)目標(biāo)跟蹤算法[J].電子與信息學(xué)報(bào),2017, 39(3):634-639.

YANG F, ZHANG W Y. Multiple model bernoulli particle filter formaneuvering target tracking[J]. Journal of Electronics & Information Technology, 2017, 39(3): 634-639.

[2] 冷雪冬, 巴斌, 逯志宇,等. 基于回溯篩選的稀疏重構(gòu)時(shí)延估計(jì)算法[J]. 物理學(xué)報(bào), 2016, 65(21): 701-710.

LENG X D, BA B, LU Z Y, et al. Sparse reconstruction time delay estimation algorithm based on backtracking filter[J]. Acta Physica Sinica, 2016, 65(21): 701-710.

[3] XU J, MA M D, LAW C L. AOA cooperative position localization[C]∥Proc.of the IEEE Global Telecommunications Conference on Signal Processing, 2008: 1-5.

[4] CHAN Y T, HO K C. Joint time-scale and TDOA estimation: analysis and fast approximation[J]. IEEE Trans.on Signal Processing, 2005, 53(8): 2625-2634.

[5] 嚴(yán)航, 朱珍珍. 基于積分抽取的時(shí)/頻差參數(shù)估計(jì)方法[J].宇航學(xué)報(bào), 2013, 34(1):99-105.

YAN H, ZHU Z Z. Fast algorithm for joint estimation of DTO and DFO based on integrate-and-dump filters[J]. Journal of Astronautics, 2013, 34(1): 99-105.

[6] HO K C, XU W W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Trans.on Signal Processing, 2004, 52(9): 2453-2463.

[7] LIN C M, HSUEH C S. Adaptive EKF-CMAC-based multisensor data fusion for maneuvering target[J]. IEEE Trans.on Instrumentation and Measurement, 2013, 62(7): 2058-2059.

[8] GUSTAFSSON F, HENDEBY G. Some relations between extended and unscented Kalman filters[J]. IEEE Trans.on Signal Processing, 2012, 60(2): 545-555.

[9] JULIER S J, UHLMAN J K. Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3):401-422.

[10] IENKARAN A, SIMON H, ROBERT J E. Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature[J]. Proceedings of the IEEE, 2007, 95(5): 953-977.

[11] 逯志宇, 王大鳴, 王建輝, 等. 基于時(shí)頻差的正交容積卡爾曼濾波跟蹤算法[J]. 物理學(xué)報(bào), 2015, 64(15): 25-32.

LU Z Y, WANG D M, WANG J H, et al. A tracking algorithm based on orthogonal cubature Kalman filter with TDOA and FDOA[J]. Acta Physica Sinica, 2015, 64(15): 25-32.

[12] GUSTAFSSON F. Particle filter theory and practice with positioning applications[J]. IEEE Aerospace and Electronic Systems Magazine, 2010, 25(7): 53-81.

[13] BOSSE J, FERRéOL A, LARZABAL P. Performance analysis of passive localization strategies: direct one step approach versus 2 steps approach[C]∥Proc.of the IEEE Statistical Signal Processing Workshop, 2011: 701-704.

[14] BAR-SHALOM O, WEISS A J. Direct emitter geolocation under local scattering[J].Signal Processing,2015,117:102-114.

[15] WANG D, ZHANG G, SHEN C Y, et al. A direct position determination algorithm for constant modulus signals with single moving observer[J]. Acta Aeronautica et Astronautica Sinica, 2016, 43(5): 1622-1633.

[16] WANG D, ZHANG R J, ZHANG T. A direct position determination approach for radio emitters in presence of mutual coupling[J]. Acta Electronica Sinica, 2017, 45(5): 1130-1138.

[17] YIN J X, WU Y, WANG D. Direct position determination of multiple noncircular sources with a moving array[J]. Circuits Systems & Signal Processing, 2017, 36(10): 4050-4076.

[18] LU Z Y, WANG J H, BA B, et al. A novel direct position determination algorithm for orthogonal frequency division multiplexing signals based on the time and angle of arrival[J]. IEEE Access, 2017, PP(99): 1-9.

[19] TIRER T, WEISS A J. Performance analysis of a high-resolution direct position determination method[J]. IEEE Trans.on Signal Processing, 2017, 65(3): 544-554.

[20] WEISS A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5): 513-517.

[21] WEISS A J, AMAR A. Direct position determination of multiple radio signals[J]. Eurasip Journal on Advances in Signal Processing, 2005, 2005(1): 37-49.

[22] AMAR A, WEISS A J. A decoupled algorithm for geolocation of multiple emitters[J]. IEEE Trans.on Signal Processing, 2007, 87(10): 2348-2359.

[23] TIRER T, WEISS A J. High resolution direct position determination of radio frequency sources[J]. IEEE Signal Processing Letters, 2016, 23(2):192-196.

[24] TZAFRI L, WEISS A J. High-resolution direct position determination using MVDR[J]. IEEE Trans.on Wireless Communications, 2016, 15(9): 6449-6461.

[25] 馮奇,曲長(zhǎng)文,周 強(qiáng). 多運(yùn)動(dòng)站異步觀測(cè)條件下的直接定位算法[J]. 電子與信息學(xué)報(bào), 2017, 39(2): 417-422.

FENG Q, QU C W, ZHOU Q. Direct position determination using asynchronous observations of multiple moving sensors[J]. Journal of Electronics & Information Technology,2017,39(2):417-422.

[26] 逯志宇,任衍青,巴斌,等.基于分段信號(hào)相關(guān)累加的變速度多站聯(lián)合直接定位方法[J].物理學(xué)報(bào), 2017, 66(2):70-79.

LU Z Y, REN Y Q, BA B, et al. An improved direct position determination method based on correlation accumulation of short-time signals with variable velocity receivers[J]. Acta Physica Sinica, 2017, 66(2):70-79.

[27] LI J Z, YANG L, GUO F C, et al. Coherent summation of multiple short-time signals for direct positioning of a wideband source based on delay and Doppler[J]. Digital Signal Processing, 2015, 48(3):58-70.

[28] VANKAYALAPATI N, KAY S, QUAN D. TDOA based direct positioning maximum likelihood estimator and the Cramer-Rao bound[J]. IEEE Trans.on Aerospace and Electronic Systems, 2014, 50(3): 1616-1646.

[29] POURHOMAYOUN M, FOWLER M. Distributed computation for direct position determination emitter location[J]. IEEE Trans.on Aerospace and Electronic Systems, 2014, 50(4): 2878-2889.

[30] SIDI A J, WEISS A J. Tracking of a moving emitter based on delay and Doppler shift using a particle filter[C]∥Proc.of the IEEE Convention of Electrical & Electronics Engineers in Israel, 2010: 001012-001016.

[31] SIDI A Y, WEISS A J. Delay and Doppler induced direct tracking by particle filter[J]. IEEE Trans.on Aerospace & Electronic Systems, 2014, 50(1): 559-572.