基于輔助匹配的1點RANSAC單目視覺導航算法

齊乃新, 張勝修, 曹立佳, 楊小岡

(1. 火箭軍工程大學控制工程系, 陜西 西安 710025;2. 四川理工學院自動化與信息工程學院, 四川 自貢 643000;3. 人工智能四川省重點實驗室, 四川 自貢 643000)

0 引 言

隨著計算機視覺的發展,單目視覺導航技術已經在機器人、可穿戴計算、增強實景以及無人駕駛汽車等眾多領域展現出了廣闊的應用前景,成為人們研究的熱點。目前,單目視覺導航方法主要分為兩大類[1]:一類是基于濾波的估計方法,通過融合圖像序列的觀測量,不斷地更新特征點和攝像機的位姿參數來估計攝像機的運動信息[2-3];另一類則是基于光束平差(bundle adjustment,BA)的估計方法,通過光流場或特征點匹配實現對載體長時間的無漂移運動估計[4-5]。

基于濾波的估計方法可以有效地利用濾波預測,估計下一幀的特征點位置,采用主動視覺匹配的方法來降低匹配的復雜度,能夠實現對攝像機位姿參數的實時在線估計。帝國理工大學的Davison教授及其領導的研究團隊在這一領域做出了比較突出的貢獻,2003年首次提出了對自由運動攝像機的6D姿態估計方法[6]。該方法采用主動視覺匹配,具有較好的實時性和魯棒性;采用基于粒子濾波的特征初始化算法,很好地解決了位姿估計的長時間尺度漂移問題,具有較高的精度。隨后,Davison教授等人又做了大量的研究工作,推動了基于視覺同步定位與地圖構建(simultaneous localization and mapping,SLAM)技術的發展[7]。在Davison教授的研究基礎上,Civera[8]提出了一種基于1點隨機抽樣一致性(random sample consensus,RANSAC)的單目視覺導航方法,實現了對運動攝像機的位姿估計。該方法結合了RANSAC和擴展卡爾曼濾波器(extended Kalman filter,EKF),解決了視覺SLAM中的數據一致性問題,較大程度上優化了數據關聯的過程[9]。同時,利用1點RANSAC[10]生成假設模型,減少了算法迭代的次數,增強了系統的穩定性。

雖然Civera提出的1點RANSAC算法在視覺導航的研究中受到了許多學者的青睞[11-13],但在實際實驗過程中面臨一個匹配失效的問題,尤其是在攝像機姿態或者環境的光照條件發生突變的情況下。這一問題是由算法中的主動視覺匹配和數據關聯原理決定的。當攝像機的運動發生突變時,主動視覺匹配極易失效,找不到有效的匹配點,對后續的EKF內點更新過程產生較大的影響,系統濾波的穩定性以及狀態估計的精度都會不同程度的降低。針對上述問題,本文提出了基于尺度不變特征變換(scale invariant feature transform,SIFT)的輔助匹配方法,采用SIFT算法提取特征點、RANSAC算法解算特征點所在圖像與當前圖像之間的基礎矩陣,然后利用此基礎矩陣求解匹配點,解決攝像機姿態突變情況下主動視覺匹配失效的問題。

1 1點RANSAC單目視覺導航算法

1.1 預測和搜索匹配點

(1)

(2)

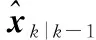
(3)

(4)

式中,Hi是hi關于xk|k-1的雅可比矩陣;Ri是觀測模型中高斯噪聲的協方差矩陣。

然后,采用主動視覺匹配方法根據預測值在特征點出現概率較高(不低于99%)的區域內搜索,找到匹配點zi,即為觀測量的真實值。

1.2 建立和估計1點狀態假設

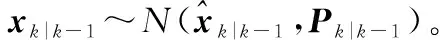
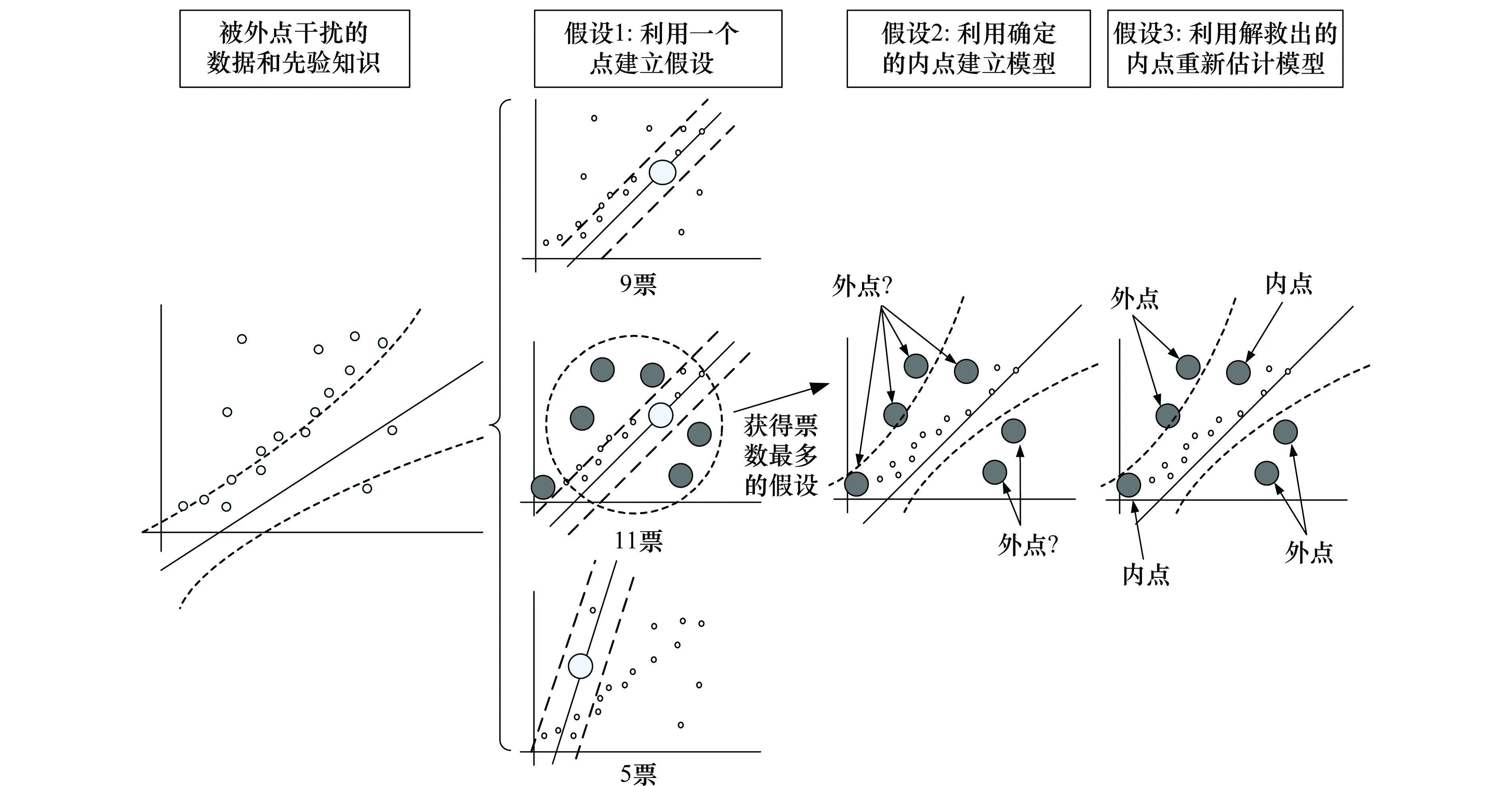
圖1 1點RANSAC估計過程Fig.1 1-Point RANSAC estimation process

在建立假設時,RANSAC算法首先為系統的模型參數建立假設,并且挑選出獲得支持率最高的一個假設。假設的建立是通過隨機的從匹配點集zIC=(z1…zi…zn)T中選出m個點完成的,m的值是計算模型參數所需的匹配點數量的最小值。通過簡單的計算統計所在閾值內的點的數量得到每一個假設的支持投票數,這里所用的閾值可以根據顯著性參數α=0.05的χ2分布得到。包含外點的假設會得到較少的投票數,如圖1的假設3。建立的假設的數量nhyp至少能夠確保在測試概率p下有一個無虛假假設,可以由式(5)計算得到。

(5)

式中,e表示點集中外點的占有比例;nhyp表示需要建立的假設數量;m表示滿足模型參數求解條件的最少匹配點數。

1.3 第1次部分更新

靠近假設模型較近的點,對假設的支持性較大,被近似認為是構成實際模型的點,這些特征點被稱為具有小觀測殘差的內點集。除此之外的點稱為外點,但是仍具有是內點的可能性。

在RANSAC假設的建立過程中,攝像機的旋轉量假設主要依靠距離較遠的特征點建立,攝像機的位移量假設主要依靠距離較近的特征點建立。由于估計的不準確性,部分距離遠的外點會呈現出小觀測殘差的特性,而距離較近的內點也有可能呈現出大觀測殘差的特性。

在假設模型和內定確定以后,利用具有小觀測殘差的內點對系統的狀態矩陣和協方差矩陣完成第1次部分更新,如式(6)～式(8)所示。

(6)

Pk|k=(I-KkHk)Pk|k-1

(7)

(8)

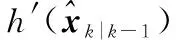
1.4 第2次部分更新

EKF預測中的誤差和協方差中的誤差在第1次部分更新完成之后得到了有效的修正,此時,存在于外點集中的具有大觀測殘差的內點可以被有效地恢復。

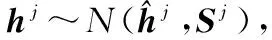
2 SIFT輔助匹配

2.1 匹配失效問題描述分析

1點RANSAC算法要求攝像機的運動是平穩連續的,這樣才能夠保證特征點在預測的區域中。但在實際情況下，攝像機并不能保證平穩連續運動,比如飛行器在遇到強風、障礙,車輛發生急轉彎、緊急剎車等情況下,載體的速度或者姿態會發生突變。此時,特征點落在預測的區域之外或有較少的點落在預測區域之中,主動視覺匹配無法搜索到落在預測區域外的點。因此,在這種情況下會找不到有效的匹配點,即使找到,數量也很少。1點RANSAC算法做出假設至少需要一對匹配點,此時的主動匹配失效,不能提供有效的匹配點對來建立假設,也就不能完成后續的更新過程。當找到的匹配點數量過少時,不能滿足概率p下確保有一個無虛假假設的條件,此時的RANSAC過程處于一種病態假設,對模型參數的估計存在較大的誤差。

1點RANSAC算法中采用主動視覺匹配作為特征點的匹配策略,通過式(3)對特征點的位置進行預測,在特征點以99%概率出現的區域內進行搜索。當攝像機的姿態發生突變時,相鄰兩幀圖像之間會有較大的差異,此時特征點將會落在預測的區域之外或有極少數的特征點落在搜索區域內。當全部的特征點都落在搜索區域外時,搜索失效,主動視覺匹配將無法找到匹配點,發生匹配失效的問題。當有極少數的特征點落在搜索區域時,由于特征點過少在后續的內點更新過程中會代入較大的誤差,影響濾波估計的精度。

上述問題在本文的主動視覺匹配失效分析實驗部分,通過對Civera提供的“rawoutput”測試數據集的實驗分析得到了充分說明。為此,本文提出輔助匹配策略,采用SIFT特征點匹配方法解決主動視覺匹配失效的問題。

2.2 SIFT輔助匹配方法

匹配失效情況的判斷依據是主動視覺匹配得到的匹配特征點數。首先,根據式(3)和式(4)預測出特征點所在的區域;然后,采用主動視覺匹配方法搜索匹配點zi;其次,對匹配點zi的數量進行統計,得到匹配點總數Nz。最后,根據匹配點總數和設定的閾值(本文中取值為5)進行判斷,如果匹配點數Nz小于設定的閾值則進行輔助匹配。輔助匹配的具體過程描述如下。

2.2.1 獲取SIFT特征點

SIFT算法是由Lowe等人在2004年提出的[15],該算法具有豐富的信息量,能夠很好地處理尺度變換、亮度變換、旋轉等情況下的圖像匹配問題。為了提高SIFT算法的效率,本文采用柵格的形式在關鍵點的鄰域內選取SIFT特征點[16],對SIFT算法的描述子進行適當地優化,如圖2所示。

將關鍵點16×16大小區域按圖2所示分成4×4的16個小區域,從中選取彼此不相鄰的8個小區域(圖中灰色小區域)對SIFT特征點進行描述。如此,能夠將SIFT特征點128維的特征描述向量壓縮為64維,降低了算法的復雜度。

圖2 SIFT特征點選取方式Fig.2 SIFT feature point selection method

然后利用式(9)剔除響應值小的點

(9)

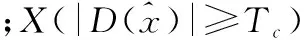
D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))?I(x,y)=

L(x,y,kσ)-L(x,y,σ)

(10)

L(x,y,σ)=G(x,y,σ)?I(x,y)

(11)

式中,I(x,y)表示一幅圖像;(x,y)表示圖像的像素坐標;σ是尺度空間因子;L(x,y,σ)表示圖像變換后的尺度空間;G(x,y,σ)為高斯核函數; ?為卷積運算。

最后,通過如式(12)中2×2的Hessian矩陣H剔除邊緣點,得到帶有描述子的SIFT特征點。

(12)

2.2.2 匹配

分別提取到兩幅圖像的SIFT特征點后,采用式(13)歐式距離進行相似性度量,獲取圖像間潛在的匹配。

(13)

式中,向量X和Y分別定義為X=(x1,x2,…,xn)和Y=(y1,y2,…,yn)。

根據相似性度量得到的初始匹配點對中存在一定程度的誤匹配,為了剔除這些誤匹配點,提高算法的魯棒性,在算法中添加了主方向約束條件[16],其具體步驟如下:

步驟1按式(14)計算匹配點集zIC=(z1…zi…zn)T的主方向差方值,即

D(i)=|O1(i)-O2(i)|2，i=1,2,…,n

(14)

式中,D(i)代表zIC=(z1…zi…zn)T的主方向差方值;O1(i)為圖像1中的特征點主方向;O2(i)為圖像2中的特征點主方向;n為匹配點集的大小;

步驟2計算誤匹配點的剔除閾值To,即

(15)

步驟3剔除初始匹配點集zIC=(z1…zi…zn)T中的誤匹配點,即

(16)

2.2.3 解算基礎矩陣及匹配點求解

基礎矩陣反映了兩幅圖像之間的變換關系,其與兩幅圖像的匹配特征點對存在如式(17)所示的約束關系。

u′Fu=0

(17)

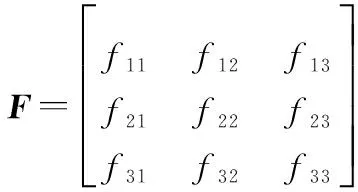
假設匹配點集的大小為n,則兩幅圖像之間滿足的約束方程為

Af=

(18)

式中,f=(f11,f12,f13,f21,f22,f23,f31,f32,f33)；A為系數矩陣。基礎矩陣的求解算法對外點比較敏感,為此文中在RANSAC算法的基礎上引入了Sampson加權算子來劃分局內點和局外點,用以減小噪聲對特征點的影響,防止由于少量誤匹配所產生的誤差影響匹配精度的問題產生。解算得到基本矩陣之后,根據初始特征點求解對應的匹配點,具體步驟如下:

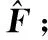
步驟2通過加權算子

(19)

計算Sampson距離,將zIC=(z1…zi…zn)T分為局內點和局外點,對基本子集進行投票;

步驟3將當前投票數與最大投票數進行比較,保存更新對應投票數最多的基礎矩陣和局內點;

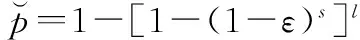
步驟5根據對應投票數最大的局內點,重新計算基礎矩陣F;

步驟6根據步驟5得到的基礎矩陣F解算用于狀態更新的有效匹配特征點。

2.2.4 EKF狀態更新

輔助匹配找到有效匹配特征點之后對狀態方程和協方差矩陣進行一次更新，更新方程如式(20)～式(22)所示。

(20)

Pk|k=(I-KkHk)Pk|k-1

(21)

(22)

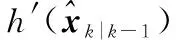
2.2.5 建立狀態假設

最后建立狀態假設,完成1點RANSAC單目視覺導航算法的兩次內點更新,得到狀態方程的最終估計量。

3 實驗驗證分析

3.1 主動視覺匹配失效分析實驗

為充分說明1點RANSAC算法中的主動視覺匹配失效問題,本文采用Civera提供的rawoutput測試數據集進行了實驗分析,實驗結果如圖3～圖5所示。

圖3 主動視覺匹配失效幀的圖像Fig.3 Image in active vision matching failure frame

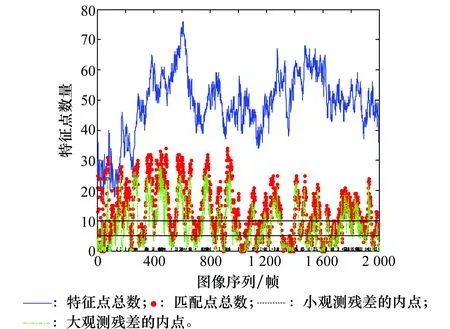
圖4 特征點的統計情況Fig.4 Statistics of feature points

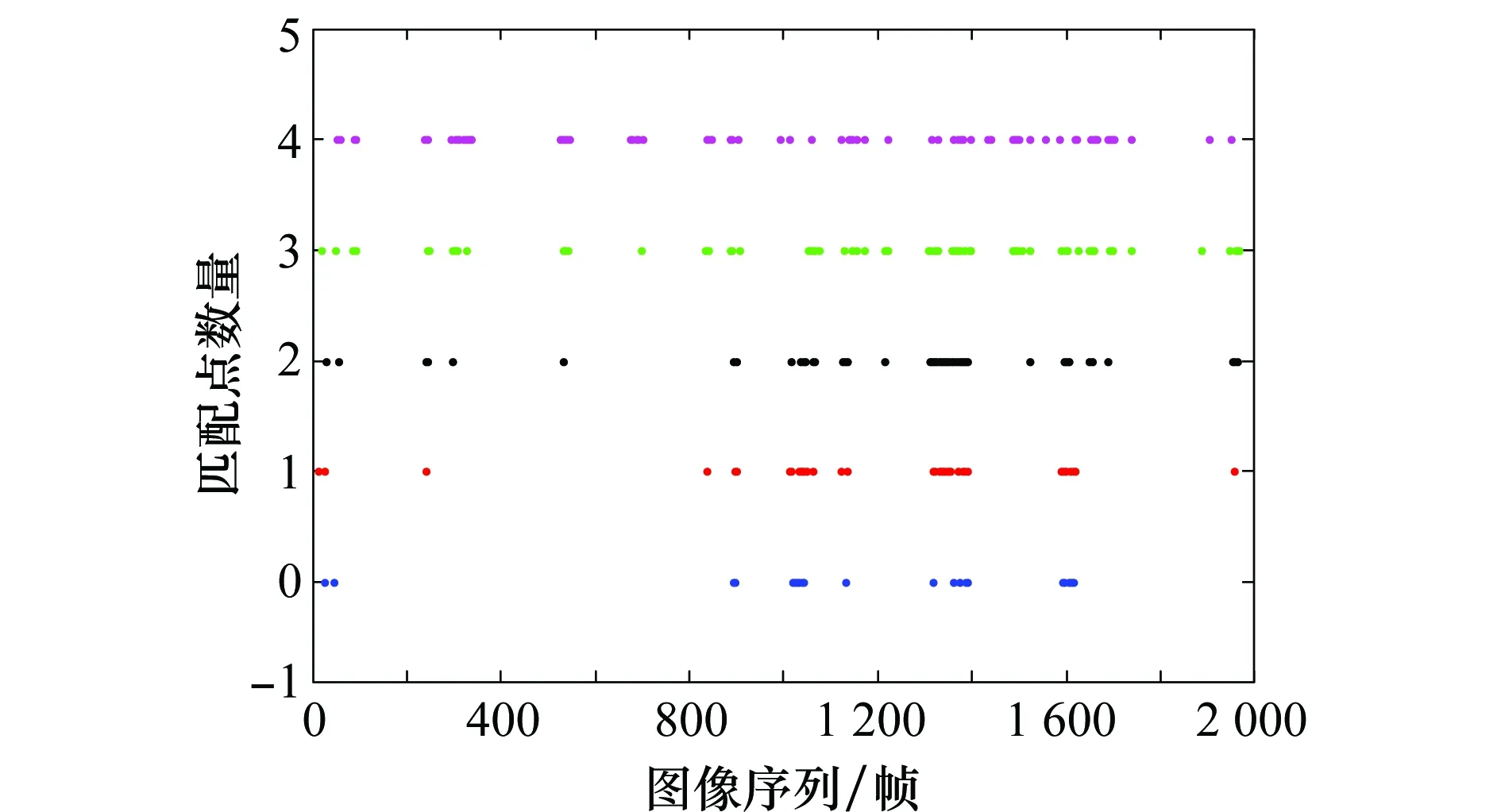
圖5 主動視覺匹配找到的匹配點少于5個時的統計情況Fig.5 Statistics of the matching points under 5 found by the active visual matching

圖3給出了主動視覺匹配得到的匹配點數在5個之內(包括5個)的幾幀圖像,從第1～6行分別是0～5個匹配點的情況,圖中藍色表示未能找到匹配點的特征點、粉紅色表示找到的匹配點是外點的特征點、紅色表示找到的匹配點是內點的特征點。從圖3中可以看出,雖然具有較多的特征點,但由于攝像機的運動突變以及外界環境的干擾,導致主動視覺匹配沒有找到有效的匹配點,或者找到的有效匹配點不足以建立一個良態假設。

圖4對整個圖像序列每一幀的特征點總數、主動視覺匹配找到的匹配點總數、具有小觀測殘差的內點數以及具有大觀測殘差的內點數進行了統計。從統計情況來看,主動視覺找到的匹配點數在10個以內的情況出現次數較多,而匹配點數少于10時,RANSAC假設的建立以及利用內點更新的過程會出現病態情況,影響了算法的估計精度。由此可以知道,在1點RANSAC單目視覺導航算法中主動視覺匹配失效問題比較嚴重,并且會對估計精度造成一定的影響,需要采取必要的措施加以解決。

圖5是對匹配點數在5個之內出現的幀數的一個統計情況,從圖中可以分析出主動視覺失效是階段性的,存在于攝像機運動發生突變,或者環境發生突變時的情況下。在本實驗中主動視覺匹配失效問題在第800～1 700幀時出現比較密集,原因在于這一段中攝像機的運動突變情況較多,平滑穩定性較差,并且多次出現角度和運動方向逆轉的情況。

為了進一步說明1點RANSAC算法中的匹配失效問題對整個算法的影響程度,表1對主動視覺匹配找到的匹配點少于10個時的幀數,以及在圖像序列中的占比情況作了統計。

表1 匹配點數在10個以內的幀數統計結果

整個數據集總共2 169幀圖像,沒有找到匹配點的情況共44幀,找到一個匹配點共61幀,找到2個匹配點共75幀,找到3個匹配點共101幀,找到4個匹配點共106幀,找到5個匹配點共117幀。從統計結果來看,完全沒有找到匹配點的情況占2.03%,匹配點在5個以內(包含5個)占23.25%,匹配點在10個以內(包含10個)占46.26%。可見主動視覺匹配失效的情況發生的次數較多,對算法的影響比較大,如果不采取一定的措施來解決這一問題,會較大程度上影響單目視覺導航算法的估計精度和穩定性。為此,本文提出一種基于SIFT的輔助匹配策略,解決了1點RANSAC單目視覺導航算法中的匹配失效問題。

3.2 輔助匹配效果分析實驗

本文采用Civera提供的rawoutput測試數據集進行了匹配實驗。取第892幀為當前圖像,此時1點RANSAC算法發生了匹配失效問題,采用主動視覺匹配未能找到匹配點。取892幀時的特征點第一次被觀測到時所在圖像為待匹配圖像,采用本文提出的輔助匹配算法查找匹配點。

實驗統計可知第892幀時,特征點總數為40,SIFT匹配找到的特征點總數為35。如圖6所示,分別是第98、679、739和862幀上的特征點的SIFT匹配結果,這4組圖像發生了較大程度的平移、旋轉、尺度縮放以及視角變化,從實驗結果來看,匹配精度較高,能夠有效地找到匹配點。

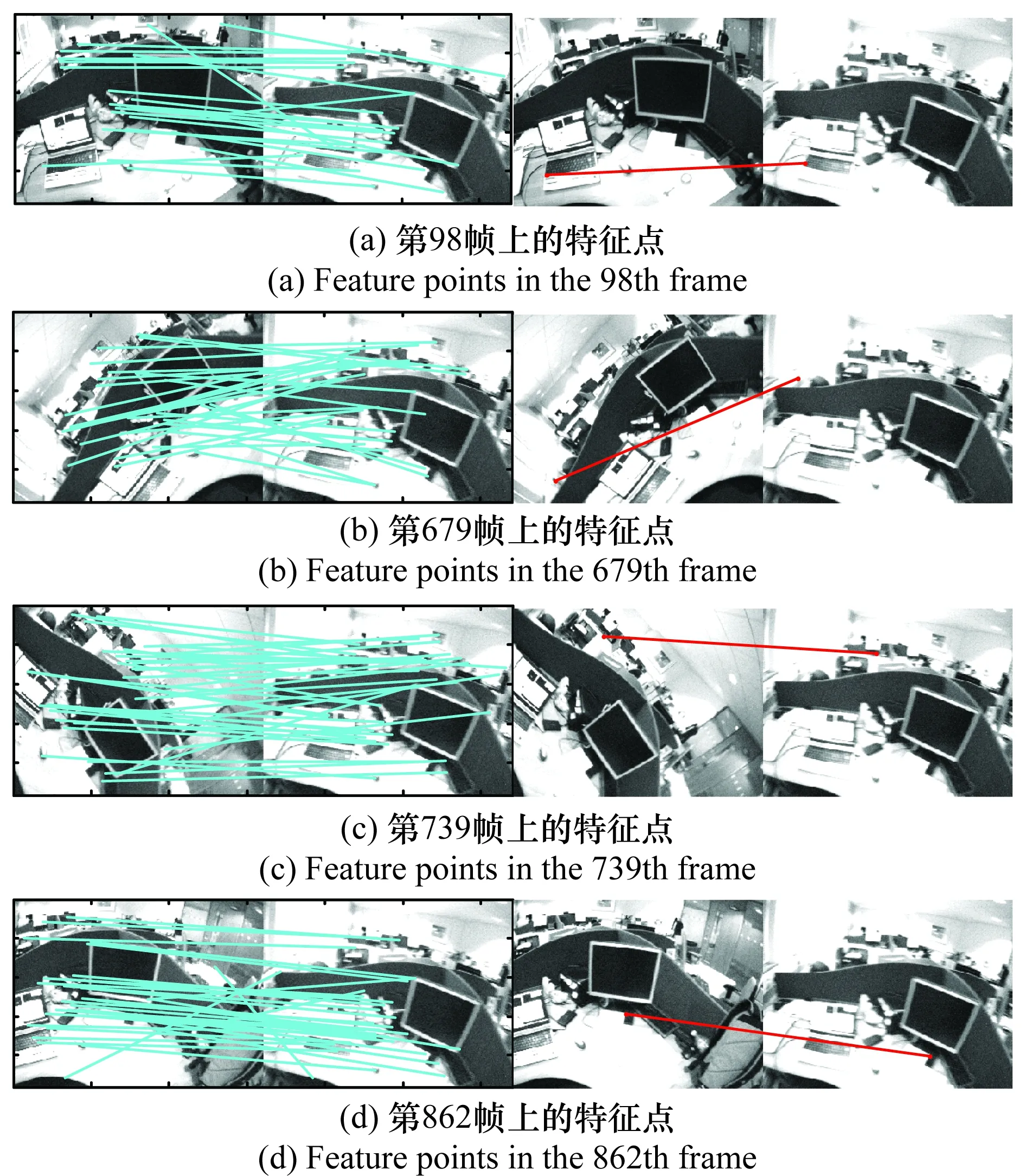
圖6 SIFT匹配結果Fig.6 Matching results of SIFT algorithm

圖7對SIFT匹配的精度進行了統計分析,從分析結果來看，35個特征點中有3個點的誤差超出了10個像素,其他點的誤差均在5個像素之內,分析原因為誤差超過10個像素的特征點所在的圖像與當前圖像的重疊區域較少,SIFT匹配過程中找到的匹配點數少于15,此時RANSAC算法解算基礎矩陣時不能有效地剔除誤匹配,引入了較大的誤差。此問題可以在SIFT輔助匹配過程,通過設定SIFT匹配點數的閾值來解決。

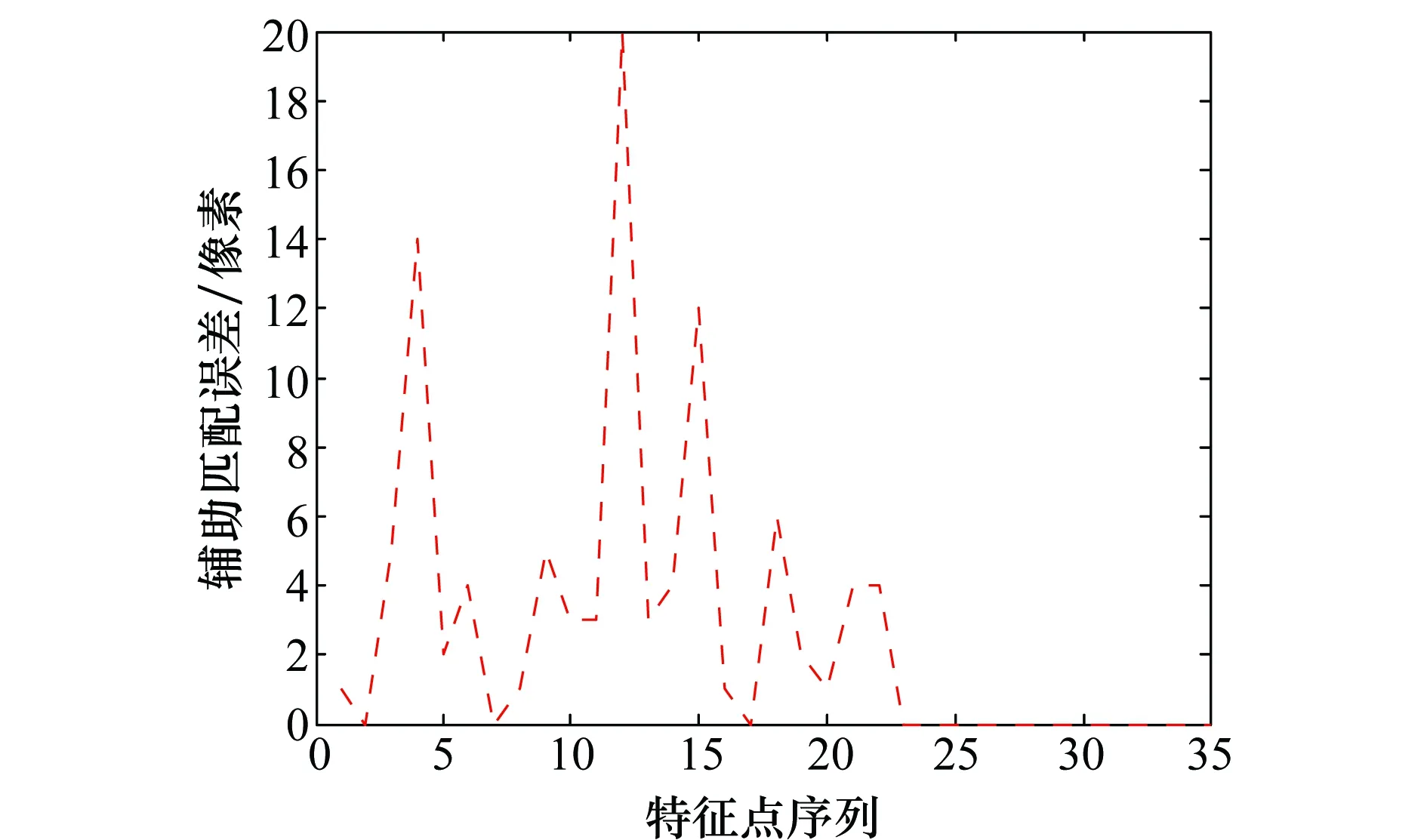
圖7 SIFT匹配解算的匹配點誤差Fig.7 Errors of matching points calculated by SIFT algorithm

采用添加輔助匹配后的1點RANSAC算法重新對Civera提供的rawoutput測試數據集進行了導航估計,并重新對整個數據集中每一幀的特征點總數、SIFT輔助找到的匹配點總數、具有小觀測殘差的內點數以及具有大觀測殘差的內點數進行了統計,結果如圖8和圖9所示。從圖8輔助匹配后特征點的統計情況來看,不存在匹配點數在5個以下的情況。圖9對應的是圖2的幀數,從匹配點的顯示結果來看,每一幀都能夠找到有效的特征點進行算法后續的狀態更新,較好地解決了1點RANSAC單目視覺導航算法中存在的主動視覺匹配失效問題。

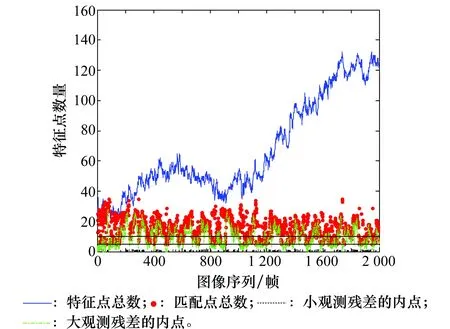
圖8 輔助匹配后的特征點統計情況Fig.8 Statistics of feature points with aided matching

圖9 主動視覺匹配失效幀的輔助匹配結果Fig.9 Results of the images in active visual matching failure frame with aided matching

3.3 智能實驗平臺驗證實驗

為了驗證輔助匹配方案對提高EKF算法估計精度的有效性,本文設計了一組驗證性實驗,實驗采用載有單目攝像機的智能實驗平臺,如圖10所示。本實驗平臺是根據需要自主改裝的由DrRobot公司生產的X80 Pro型WiFi智能控制小車。該智能實驗平臺包含單目攝像機和通信控制模塊,能夠通過編程預定行駛軌跡模擬平臺的運動軌跡,并且能夠通過WiFi實時傳輸圖像序列,用于估計平臺的位姿參數。車載攝像頭采用電荷耦合器件(charge coupled device,CCD)針孔攝像頭,其模型為針孔攝像頭模型,焦距:fx=330.524,fy=329.791;中心點:Cx=159.5,Cy=119.5;畸變參數:k1=-0.103,k2=0.138;采集到的圖像大小:320像素×240像素。

圖10 智能實驗平臺Fig.10 Intelligent experimental platform

本驗證實驗是在室內環境下完成的,環境相對比較復雜,包括實驗儀器、辦公桌、電腦等靜態物體,以及人員走動、光照的變化等動態環境。實驗中,機器人平臺的運動軌跡分為3個階段:第1階段先往前直行8 m,然后進入第2階段,進行一次90°轉彎,第3階段再往前直行6 m。分別采用本文改進算法和標準的1點RANSAC算法(原算法)對攝像機的姿態角進行估計,實驗結果如圖11～圖17所示。機器人運行軌跡如圖18所示。

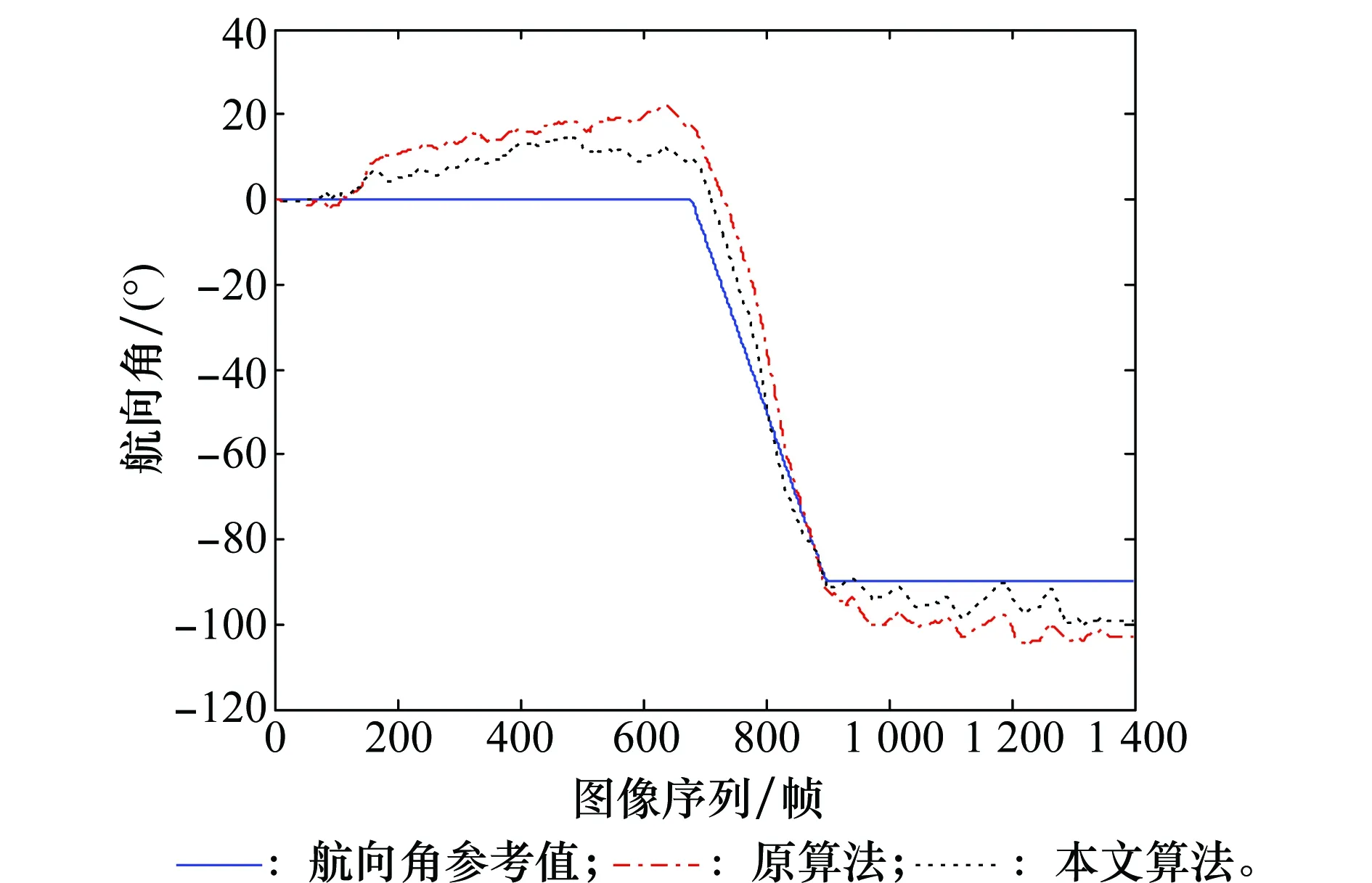
圖11 攝像機航向角的估計結果Fig.11 Estimation results of camera’s course angle

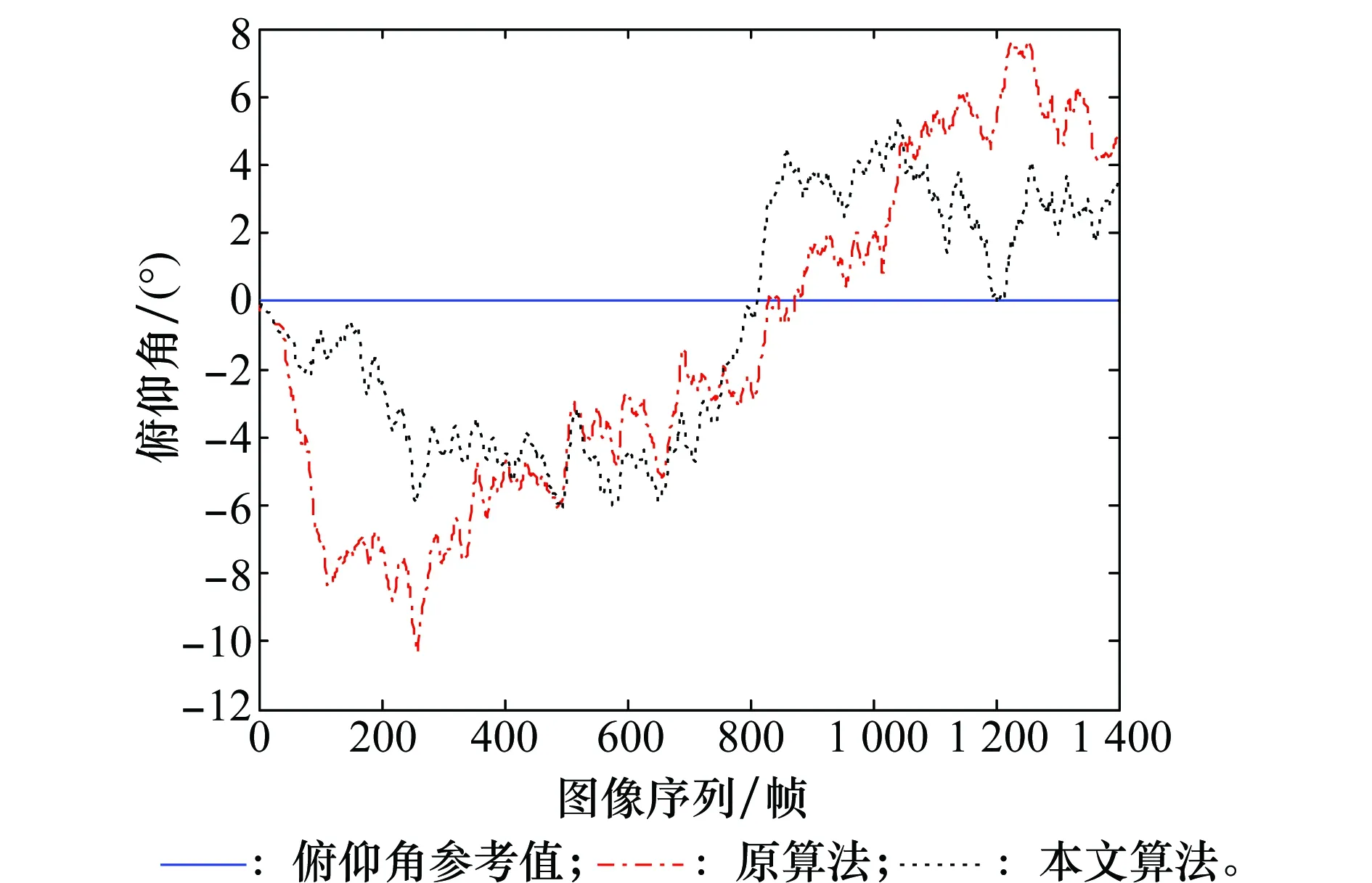
圖12 攝像機俯仰角的估計結果Fig.12 Estimation results of camera’s pitch angle

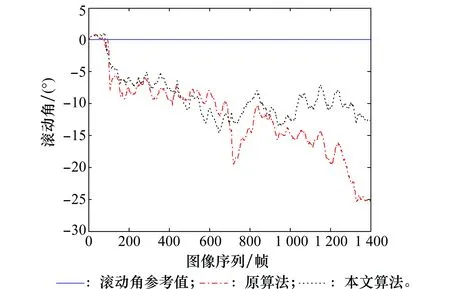
圖13 攝像機滾動角的估計結果Fig.13 Estimation results of camera’s roll angle

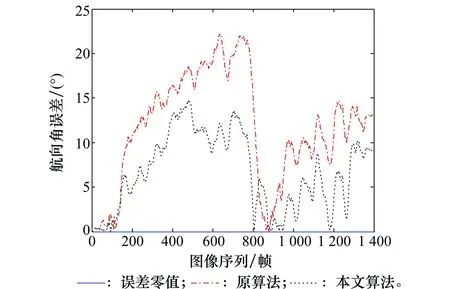
圖14 攝像機航向角的估計誤差Fig.14 Estimation errors of camera’s course angle

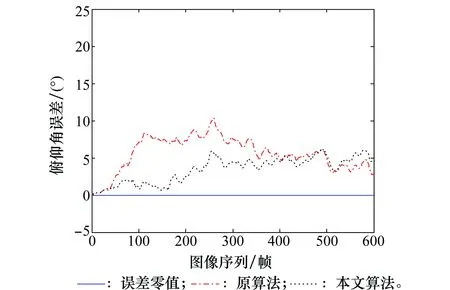
圖15 攝像機俯仰角的估計誤差Fig.15 Estimation errors of camera’s pitch angle

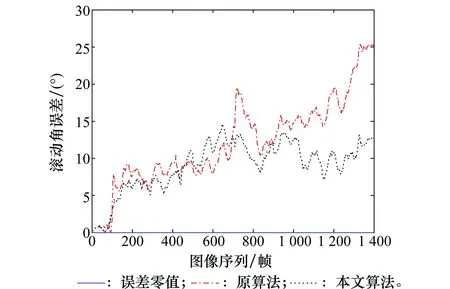
圖16 攝像機滾動角的估計誤差Fig.16 Estimation errors of camera’s roll angle

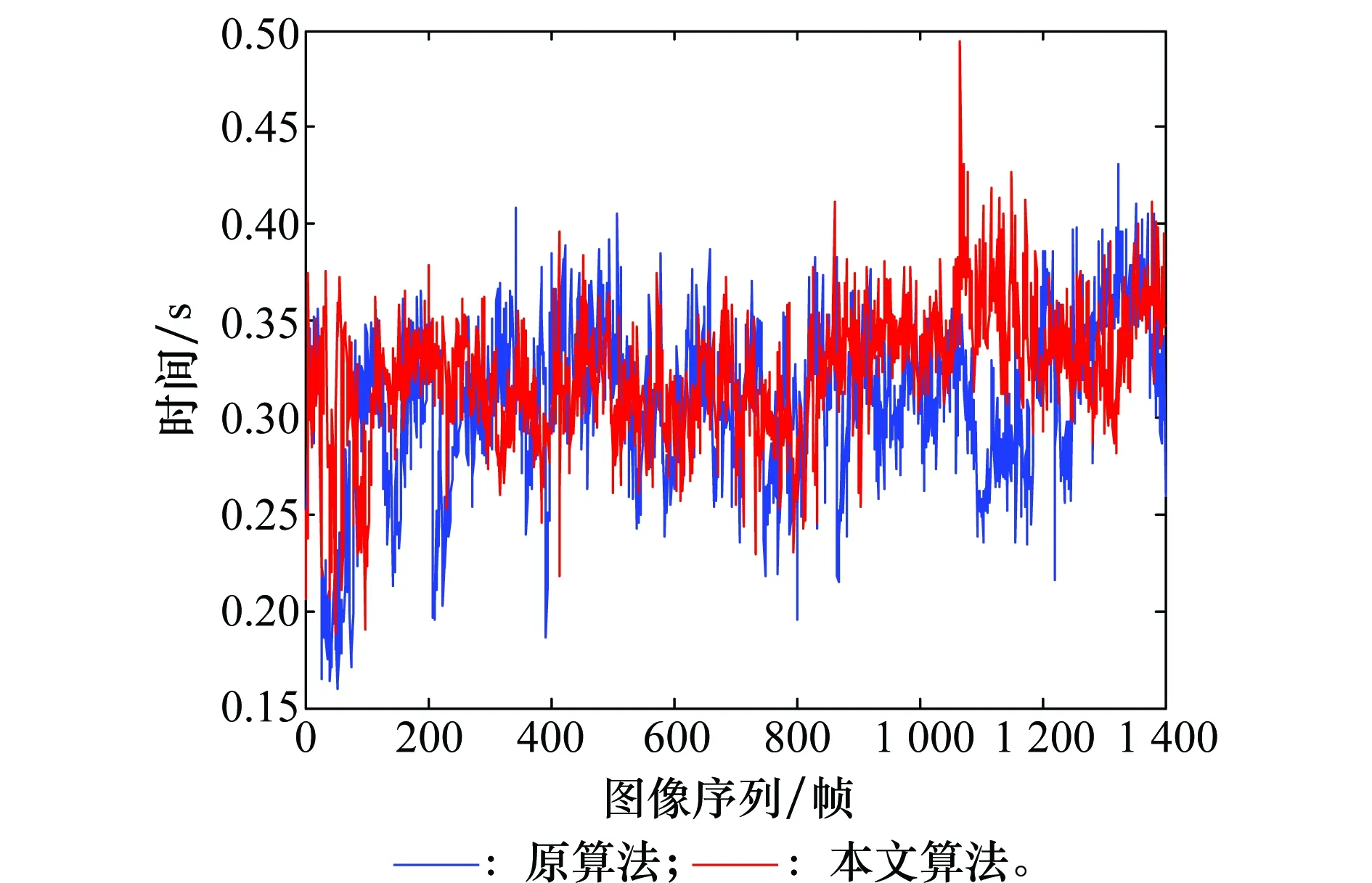
圖17 算法對單幀圖像的計算時間Fig.17 Computational times for single frame of the algorithms

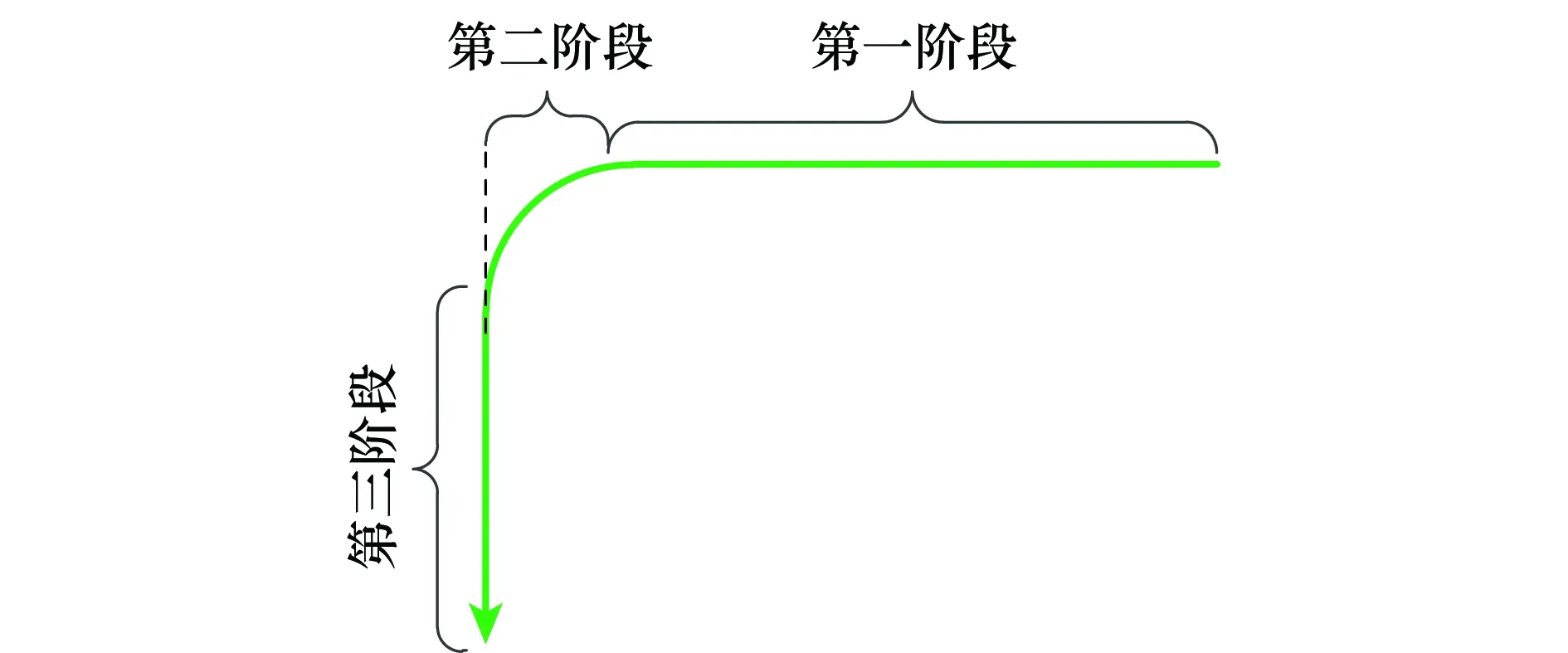
圖18 機器人運行軌跡示意圖Fig.18 Sketch map of robot’s motion trail

圖11～圖13為本文算法和原算法對攝像機姿態角的估計結果對比圖,從圖中可以看出,本文改進算法的估計精度要高于原算法。圖14～圖16為本文算法和原算法對攝像機姿態角的估計誤差對比圖,改進算法估計的攝像機航向角、俯仰角和滾動角的平均誤差為6.73°、3.25°和9.01°,標準的1點RANSAC算法估計的攝像機航向角、俯仰角和滾動角的平均誤差為11.77°、4.46°和12.04°。由此可知,添加輔助匹配后的EKF算法提高了對攝像機的俯仰、偏航以及滾動3個姿態角的估計精度,其中航向角平均誤差減小5.04°,俯仰角平均誤差減小1.21°,滾動角平均誤差減小3.03°。

為了比較本文算法和標準的1點RANSAC算法的計算效率,圖17給出了本文算法和原算法對單幀圖像的運算時間。其中，本文算法的運算時間中不包括SIFT匹配的時間,因為SIFT算法固有的復雜性,其運算比較耗時,文中仿真平臺為Matlab,其效率較低,算法仿真成熟后將移植到C++平臺,然后采用多線程并行處理SIFT匹配問題,不影響EKF濾波的過程,因此暫時不將SIFT算法的運算時間考慮在內。本文算法的平均耗時為0.32 s,原算法的平均耗時為0.31 s,由此可見,本文改進算法EKF濾波估計階段保持了原算法的計算效率。

上述3組實驗可以說明,標準的1點RANSAC算法中存在主動視覺匹配失效的問題,影響估計的精度,本文提出的輔助匹配方法能夠找到精度較高的匹配特征點,有效地解決了1點RANSAC單目視覺導航算法中的匹配失效問題,在較大程度上提高了EKF算法對攝像機姿態角的估計精度。

4 結 論

本文從理論與實驗相結合的角度出發,分析了1點RANSAC單目視覺導航算法中存在的匹配失效問題,提出了一種基于輔助匹配的1點RANSAC單目視覺導航算法。該算法采用SIFT算法提取特征點,RANSAC算法求解特征點所在圖像與當前圖像之間的基礎矩陣,然后利用基礎矩陣求解匹配點,有效地解決了攝像機姿態突變時由于數據關聯失敗引起的匹配失效問題,提高了EKF算法對攝像機運動姿態角的估計精度。

參考文獻：

[1] STRASDAT H, MONTIEL J M M, DAVISON A J. Visual SLAM: why filter[J]. Image and Vision Computing, 2012, 30(2): 65-77.

[2] CIVERA J, GRASA O G, DAVISON A J, et al. 1-point RANSAC for EKF-based structure from motion[C]∥Proc.of the IEEE/RSJ International Conference on Intelligent Robots and Systems, 2009: 3498-3504.

[3] PIRE T, FISCHER T, CIVERA J, et al. Stereo parallel tracking and mapping for robot localization[C]∥Proc.of the IEEE/RSJ International Conference on Intelligent Robots and Systems, 2015: 1373-1378.

[4] LIM J, FRAHM J M, POLLEFEYS M. Online environment mapping[C]∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition, 2011: 3489-3496.

[5] GRASA O G, BERNAL E, CASADO S, et al. Visual SLAM for handheld monocular endoscope[J]. IEEE Tran.on Medical Imaging, 2014, 33(1): 135-146.

[6] DAVISON A J. Real-time simultaneous localisation and mapping with a single camera[C]∥Proc.of the IEEE Computer Vision, 2003: 1403-1410.

[7] HANDA A, CHLI M, STRASDAT H, et al. Scalable active matching[C]∥Computer Visionand Pattern Recognition, 2010: 1546-1553.

[8] CIVERA J, GRASA O G, DAVISON A J, et al. 1-Point RANSAC for extended Kalman filtering: application to real-time structure from motion and visual odometry[J]. Journal of Field Robotics, 2010, 27(5): 609-631.

[9] CIVERA J, DAVISON A J, MONTIEL J M M. Inverse depth parametrization for monocular SLAM[J]. IEEE Trans.on Robotics, 2008, 24(5): 932-945.

[10] FRAUNDORFER F, SCARAMUZZA D. Visual odometry: part II: matching, robustness, optimization, and applications[J]. IEEE Robotics & Automation Magazine, 2012, 19(2): 78-90.

[11] 李捐. 基于單目視覺的移動機器人 SLAM 問題的研究[D]. 哈爾濱:哈爾濱工業大學, 2013.

LI J. Reserch on SLAM problem of mobile robot with monocular vision[D]. Harbin: Harbin Institute of Technology, 2013.

[12] CONCHA A, DREWS-JR P, CAMPOS M, et al. Real-time localization and dense mapping in underwater environments from a monocular sequence[J].Oceans, 2015：1-5.

[13] SENGUPTA A, ELANATTIL S. New feature detection mechanism for extended Kalman filter based monocular SLAM with 1-Point RANSAC[C]∥Proc.of the International Conference on Mining Intelligence and Knowledge Exploration, 2015: 29-36.

[15] LOWE D G.Distinctive image features from scale-invariant keypoint[J].International Journal of Computer Vision,2004,60(2):91-110.

[16] 齊乃新, 曹立佳, 楊小岡, 等. 基于方向約束的改進SIFT匹配算法[J]. 計算機科學, 2014, 41(S1): 125-128.

QI N X, CAO L J, YANG X G, et al. The improved SIFT matching algorithm based on orientation constraint[J]. Computer Science, 2014, 41(S1): 125-128.