基于自適應分割與偏移場估計的活動輪廓模型

蔡 青, 劉慧英, 孫景峰, 周三平, 李 靖

(1. 西北工業大學自動化學院, 陜西 西安 710072; 2. 西安交通大學人工智能與機器人研究所,陜西 西安 710049; 3. 西北工業大學機電學院, 陜西 西安 710072)

0 引 言

圖像分割是計算機視覺領域的一項基本而又關鍵的技術[1],其在現實數字世界中扮演著重要角色,例如:視頻監控[2]、目標跟蹤[3]和醫學圖像分割[4-7]等。受成像條件和成像設備的影響,所得圖像會呈現不同程度的灰度不均勻,嚴重影響了圖像的分割效果。鑒于活動輪廓模型參數少、穩定性好等優點,其已逐漸成為分割灰度不均勻圖像的必選方法。現存的活動輪廓模型大體可分為邊緣型[8-12]和區域型[13-18]兩類。

邊緣型利用圖像梯度構造能量泛函,用于分割邊界辨識度高的圖像。例如,文獻[10]提出的幾何積分模型,通過最小化邊界和圖像梯度間夾角的方式提出模型,完成目標分割。與邊緣型不同,區域型則利用圖像區域信息構造能量泛函,實現了對弱邊界圖像的分割。例如,文獻[13]提出的Chan-Vese (CV)模型,利用圖像全局信息引導圖像分割,完成了對邊界辨識度低圖像的分割。然而,該模型對灰度不均勻圖像不起作用。為此,文獻[14]通過將圖像局部灰度信息融入CV模型,提出了著名的區域可擴展擬合(region-scalable fitting, RSF)模型,實現了對灰度不均勻圖像的分割。但是,局部信息的引入降低了模型對初始輪廓的魯棒性和分割效率。

為此,本文提出了一種新型混合活動輪廓模型,其具有以下創新點:

(1) 通過對圖像進行模糊聚類分析,構造了一種帶有模糊隸屬度函數的新型偏移場估計模型,成功地提取了圖像的偏移場,提高了模型的分割準確度。

(2) 基于圖像信息熵構造的自適應尺度算子(adaptive scaling operator, ASO),實現了對模型尺度的自適應調整,提高了模型的魯棒性和分割效率。

對灰度不均勻圖像的分割結果表明,本文模型對初始輪廓和不同種類噪聲具有較好的魯棒性。此外,與經典模型的對比實驗表明,本文模型在分割速度和準確度上具有較大的優勢。

深度學習是目前比較流行的算法,本文基于以下3點考慮未與其進行比較:

(1) 深度學習的訓練需要大量帶有標注的訓練樣本[19-20],而本文所用的灰度不均勻圖像,數量少且其大多數標準分割結果都是前人手動分割,并不適用于深度學習的訓練。

(2) 本文模型的比較實驗都是基于橫向比較,即活動輪廓模型間的比較,若與深度學習算法比較,則違背了活動輪廓模型間的比較原則。

(3) 對于小樣本數據的灰度不均勻圖像,基于經典活動輪廓模型的分割算法,不僅成本低、準確度高,而且更具有應用價值。

當然,隨著活動輪廓模型和深度學習的發展以及大型標注的灰度不均勻圖像庫的出現,兩者的比較或者融合會越來越多,畢竟深度學習在大數據上的優勢還是非常明顯的。

1 背 景

1.1 RSF模型

文獻[14]通過將局部灰度信息融入CV模型,提出了RSF模型,彌補了CV模型的缺陷,具體能量泛函為

(1)

式中,λ1、λ2是大于等于零的常數;Kσ(y-x)是高斯核函數,控制能量泛函的領域范圍;f1(x)、f2(x)是點x的小鄰域內演化曲線內、外的灰度均值;H(x)是Heaviside函數;φ(x)是Lipschitz函數;δ(x)是Dirac函數。然而,由于RSF采用固定尺度控制局部鄰域,影響了其對灰度不均勻圖像的分割效果。

1.2 信息熵理論

信息熵是香農在文獻[21]中提出的用來度量信息不確定性的概念。假設X是一個離散隨機變量,即其取值范圍R={x1,x2…}是有限可數的,設Pi=P{X=xi},則X的熵定義為

(2)

定理1對于圖像的一個局部窗口,當且僅當局部窗口內的所有灰度值均相等時,窗口的熵值最大[18]。

2 本文模型

本文混合活動輪廓由數據擬合項和正則項兩部分組成,即

E=ED+ER

(3)

式中,ED和ER分別是數據擬合項和正則項。

2.1 偏移場估計模型

如引言部分所述,由于受各種因素影響,圖像都有不同程度的灰度不均勻現象,其嚴重影響了模型的分割效果。為此,學者們提出了一種被廣泛接受的數學模型,來矯正圖像的這種灰度不均勻現象。假設x∈Ω是圖像域Ω中的點,則該點的灰度不均勻模型可以表示為

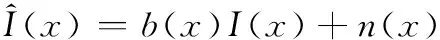
(4)

(1)I(x)是分段常值,即I(x)=ci,x∈Ωi,其中,Ωi是圖像域Ω的一個區域。

(2)b(x)在圖像域Ω中是連續、光滑的。

在實際圖像中,I(x)并不是相互獨立的分段常值,用常值表示圖像灰度是不準確的,會降低模型的分割準確度,甚至導致模型的分割失敗。為此,在對圖像進行模糊聚類分析后,本文用一個模糊隸屬度函數來描述圖像劃分之間的依賴關系,即

(5)

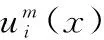
2.2 ASO

通過將香農信息熵應用到圖像領域,本文提出了圖像信息熵,即

(6)

式中,Py, Ωx是圖像的灰度概率分布,定義為

(7)

然后,基于背景中的定理1,提出了ASO,即

(8)

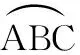
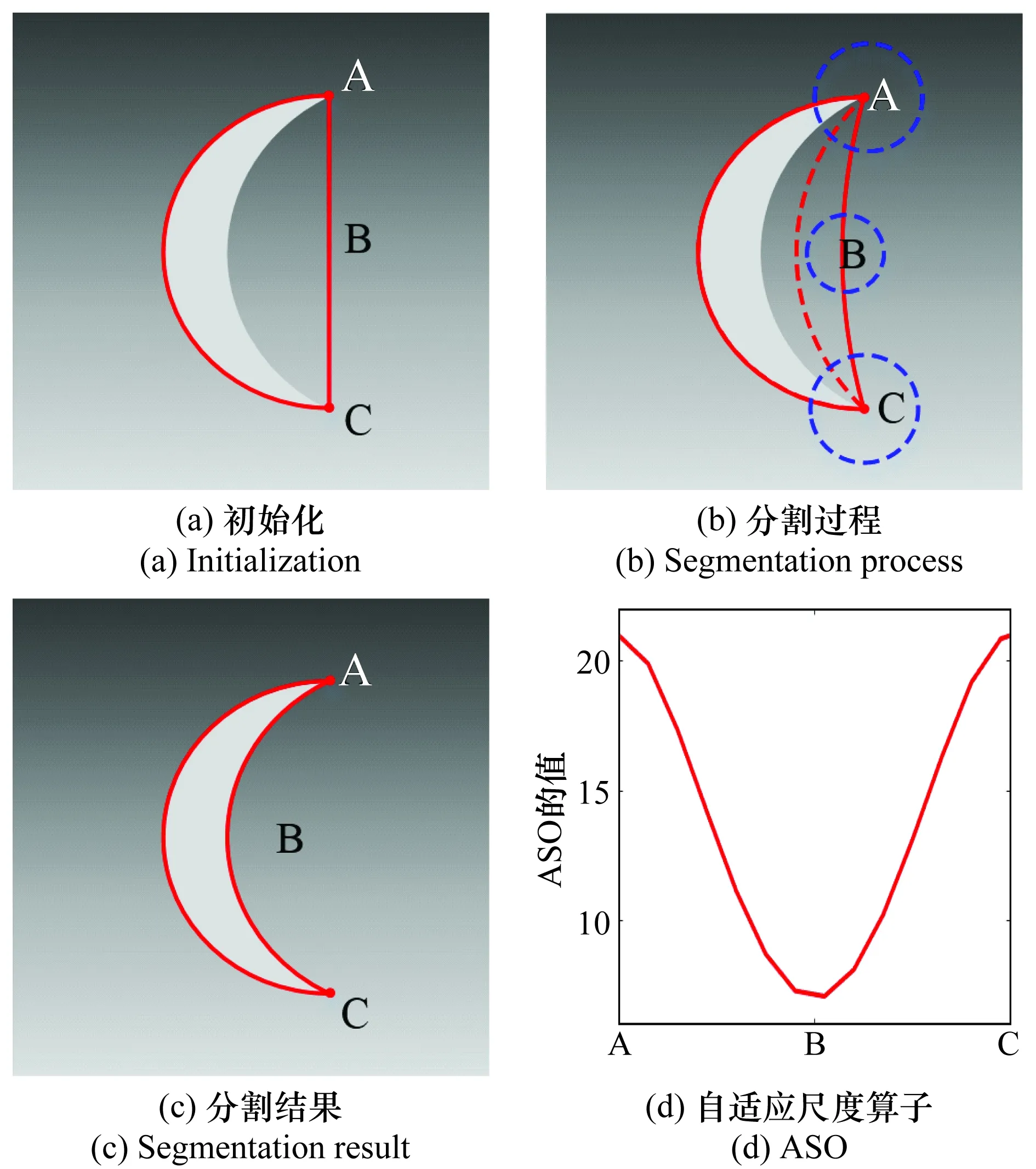
圖1 ASO的工作原理Fig.1 Work principle of the ASO

2.3 數據擬合項

將偏移場估計模型和ASO融入一個能量泛函,提出本文模型的數據擬合項為

(9)

式中,λi是非負常數;N表示圖像域Ω被劃分的類別數,若圖像只有目標和背景兩類,則N=2。

2.4 正則項

為了保證數值計算的穩定性和演化曲線的光滑性,正則項是活動輪廓模型必不可少的組成部分。本文正則項由懲罰項和調整項兩部分組成,即

ER=μEP+νER

(10)

式中,μ、ν為正數,用于調整控制懲罰項EP和調整項EL之間的權重。兩項的具體表達式分別為

(11)

(12)

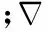
(13)

則本文混合活動輪廓模型具體表達式為

E=ED+ER=

(14)

3 模型的實現

3.1 模型的水平集實現

為計算式(14),需引入水平集方法,即用隱式表達式表示方程,省去復雜而又耗時的解參過程。

首先,用Lipschitz函數和Heaviside函數隱式表示Ωi,對于圖像Ω在僅考慮目標和背景兩類時,即N=2,式(14)變為

(15)

式中,Mi是Ωi的隸屬函數,M1(φ)=H(φ),M2(φ)=1-H(φ);φ和H分別是Lipschitz函數和Heaviside函數,即

(17)

式中,C是演化曲線。

Heaviside函數和Dirac函數的具體定義為

(18)

(19)

其次,應用Euler-Lagrange方程和梯度下降流,解得b(x)、ui(x)和ci的表達式為

(20)

(21)

(22)

式中,*表示卷積。

最后,通過變分原理得到式(15)的梯度下降流,進而得到曲線的最終演化方程為

(23)

(24)

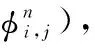
(25)

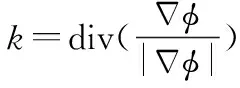
(26)

式中，φx,φy,φxx,φyy,φxy分別為二階中心差,具體表達式為

(27)

(28)

(29)

多類目標分割和兩類目標分割類似,在此不再詳述。

3.2 模型的實現步驟

模型水平集的具體實現步驟如下：

輸入讀入灰度不均勻圖像并初獲取初始輪廓φ0。

步驟1初始化相關參數。

步驟2如果|length(φi+1)-length(φi)|>η,那么

(1) 根據式(6)～式(8)計算ASO;

(2) 根據式(20)～式(22)更新參數;

(3) 根據式(26)～式(29)計算曲率;

(4) 根據式(25)更新演化曲線。

步驟3結束循環。

輸出輸出最終結果φ=φi+1。

4 實 驗

本節將從魯棒性、分割速度和分割準確度等方面,驗證模型對不同程度灰度不均勻圖像的分割效果,包括自然圖像、人工圖像、醫學圖像、紅外圖像和遙感圖像。實驗環境:Matlab R2011b (計算機CPU Intel Core i-3 2.1 GHz,內存2GB,操作系統Windows7)。實驗參數:時間步長Δt=0.1,網格間距h=1,ε=3,標準差σ=2。

4.1 實驗及結果分析

4.1.1 對初始輪廓魯棒性的驗證

圖2(a)～圖2(e)表示不同位置和不同形狀的初始輪廓,圖2(f)是其最終分割結果。由分割結果可知,本文模型對不同位置和不同形狀的初始輪廓具有一定的魯棒性。

圖2 模型對初始輪廓位置和形狀的魯棒性Fig.2 Robustness of the model to initial contour positions and shapes

4.1.2 對噪聲魯棒性的驗證

圖3(a)～圖3(d)分別被泊松噪聲、斑點噪聲、椒鹽噪聲和高斯噪聲污染過的灰度不均勻圖像。

圖3(e)～圖3(h)經過20、32、41、58次迭代后的分割結果。由實驗結果可知,噪聲并未影響模型對灰度不均勻圖像的分割效果,即本文模型對噪聲具有較強的魯棒性和抑制能力。

圖3 模型對噪聲的魯棒性Fig.3 Robustness of the model to noises

4.1.3 分割效率和分割準確度的驗證

圖4(a)是標準庫Berkeley segmentation data set 500中3幅灰度不均勻圖像,圖4(b)～圖4(d)分別是CV模型、RSF模型和本文模型的分割結果。由實驗結果可知,CV模型不能分割灰度不均勻圖像,RSF模型的分割結果則出現不同程度的誤分割和過分割現象,而文中模型卻能準確、快速完成對不同程度灰度不均勻圖像的分割。

圖4 模型分割灰度不均勻圖像的準確度和效率Fig.4 Accuracy and efficiency of the model to segment inhomogeneous intensity images

為更直觀、定量地比較RSF模型和本文模型,分別記錄了兩種模型在分割圖4時的DC(Dice coefficient)值、KI(Kappa index)值、迭代次數和CPU運行時間,如表1和表2所示。其中,指標DC和KI的定義為

(30)

(31)

式中,SG、ST分別是實驗分割結果和標準分割結果中的目標區域;TP、FP和FN分別是真比例、假比例和假反例。DC和KI都是相似性指標,值越高越好。

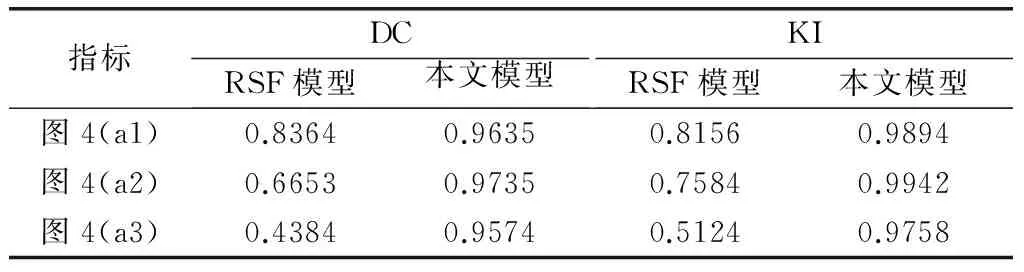
表1 分割準確度

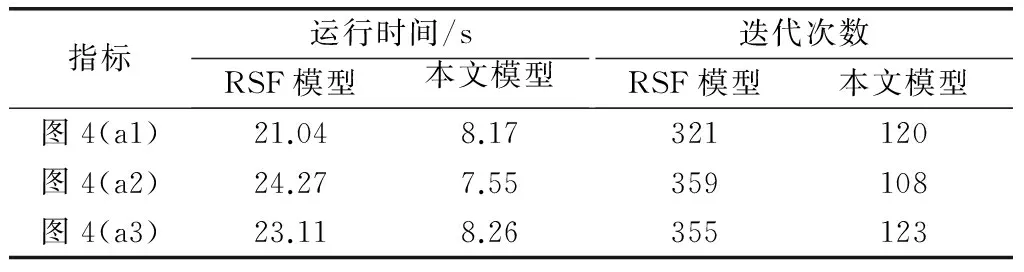
表2 分割效率

由表1和表2可知,本文模型具有較高的分割效率和分割準確度。一方面,ASO的提出,加速了曲線收斂;另一方面,新型偏移場估計模型的融入,提高了模型的分割準確度。

4.1.4 與經典模型的對比實驗

圖5(a)是2幅灰度不均勻的紅外圖像,和2幅灰度不均勻遙感圖像,圖5(b)～圖5(e)分別是局部高斯擬合(local Gaussian distribution fitting, LGDF)[15]模型、局部Chan-Vese(local Chan-Vese, LCV)[16]模型、邊界與區域水平集(boundary and region-based level set,BRLS)[18]模型和本文模型對4幅圖的分割結果。由分割結果可知,LGDF模型、LCV模型和BRLS模型在分割強灰度不均勻圖像時,并不能準確地找到模糊邊界。而本文模型卻總能準確地找到目標邊界。這歸功于新型偏移場估計模型的提出,使模型能準確提取灰度信息并完成最終分割。

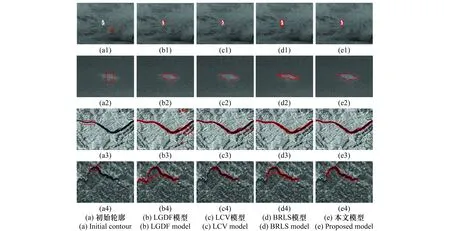
圖5 與經典模型的對比實驗Fig.5 Comparison with classical models

為更好地比較4種模型,分別記錄了其完成圖5分割時的CPU運行時間和相應迭代次數。如圖6所示,本文模型的分割效率明顯高于其他3種模型。因為本文提出的ASO,能自適應地調整模型尺度,加速演化曲線向目標邊界收斂。

圖6 分割效率Fig.6 Segmentation efficiency

4.2 模型參數分析

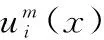
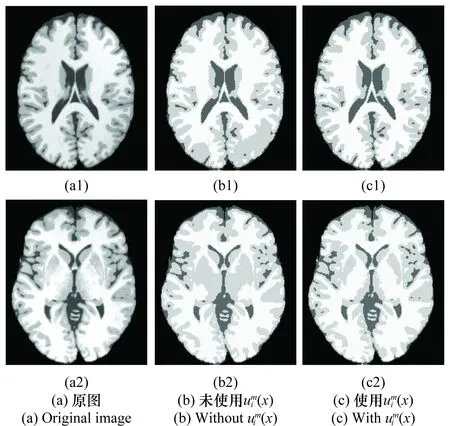
圖7 隸屬度函數的作用Fig.7 Effect of the membership function

5 結 論

本文提出了自適應分割與偏移場估計融合的新型混合活動輪廓模型,實現了對不同程度灰度不均勻圖像的快速、準確、強魯棒性地分割。其中,ASO的提出,實現了模型的自適應分割,提高了模型的分割效率。帶有隸屬度函數的新型偏移場估計模型的提出,完成了對灰度不均勻圖像偏移場的估計,提高了模型的分割準確度。最終實驗結果,驗證了模型分割灰度不均勻圖像的可行性和有效性。

參考文獻：

[1] YIN S, QIAN Y, GONG M. Unsupervised hierarchical image segmentation through fuzzy entropy maximization[J]. Pattern Recognition, 2017, 68(C): 245-259.

[2] SINGH D, MOHAN C K. Graph formulation of video activities for abnormal activity recognition[J]. Pattern Recognition, 2017, 68(C): 265-272.

[3] GONG M, QIAN Y, CHENG L. Integrated foreground segmentation and boundary matting for live videos.[J]. IEEE Trans.on Image Processing, 2015, 24(4): 1356-1370.

[4] ZHOU S, WANG J, ZHANG S, et al. Active contour model based on local and global intensity information for medical image segmentation[J]. Neurocomputing, 2016, 186(C): 107-118.

[5] ZHOU S, WANG J, ZHANG M, et al. Correntropy-based level set method for medical image segmentation and bias correction[J]. Neurocomputing, 2017, 234(C): 216-229.

[6] 蔡青,劉慧英,孫景峰,等.基于信息熵的自適應尺度活動輪廓圖像分割模型[J].西北工業大學學報,2017,35(2):286-291.

CAI Q, LIU H Y, SUN J F, et al. An adaptive scale active contour model based on information entropy for image segmentation[J]. Journal of Northwestern Polytechnical University, 2017, 35(2): 286-291.

[7] 蔡青, 劉慧英, 周三平, 等. 基于局部和全局信息的自適應水平集圖像分割[J].強激光與粒子束, 2017, 29(2): 28-35.

CAI Q, LIU H Y, ZHOU S P, et al. Adaptive level set model based on local and global intensity information for image segmentation[J]. High Power Laser and Particle Beams, 2017, 29(2): 28-35.

[8] CASELLES V, KIMMEL R, SAPIRO G. Geodesic active contours[J]. International Journal of Computer Vision, 1997, 22(1): 61-79.

[9] VASILEVSKIY A, SIDDIQI K. Flux maximizing geometric flows[J]. IEEE Trans.on Pattern Analysis and Machine Intelligence, 2002, 24(12): 1565-1578.

[10] KIMMEL R. Fast edge integration[J]. Geometric Level Set Methods in Imaging, Vision, and Graphics, 2003,7(17): 59-77.

[11] LI C, XU C, GUI C, et al. Level set evolution without re-initialization: a new variational formulation[C]∥Proc.of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition， 2005: 430-436.

[12] GAO X, WANG B, TAO D, et al. A relay level set method for automatic image segmentation[J]. IEEE Trans.on Systems, Man, and Cybernetics, Part B (Cybernetics), 2011, 41(2): 518-525.

[13] CHAN T F, VESE L A. Active contours without edges[J]. IEEE Trans.on Image Processing, 2001, 10(2): 266-277.

[14] LI C, KAO C Y, GORE J C, et al. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Trans.on Image Processing, 2008, 17(10): 1940-1949.

[15] WANG L, HE L, MISHRA A, et al. Active contours driven by local Gaussian distribution fitting energy[J]. Signal Processing, 2009, 89(12): 2435-2447.

[16] WANG X F, HUANG D S, XU H. An efficient local Chan-Vese model for image segmentation[J]. Pattern Recognition, 2010, 43(3): 603-618.

[17] LI C, HUANG R, DING Z, et al. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J]. IEEE Trans.on Image Processing, 2011, 20(7): 2007-2016.

[18] 張夢夢, 張涇周, 周三平, 等. 基于局部熵的邊界與區域水平集圖像分割模型[J]. 系統工程與電子技術, 2016, 38(12): 2884-2888.

ZHANG M M, ZHANG J J, ZHOU S P, et al. Boundary and region level set method based on local entropy for image segmentation[J]. Systems Engineering and Electronics, 2016, 38(12): 2884-2888.

[19] HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507.

[20] LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-4

[21] SHANNON C E. A mathematical theory of communication[J]. The Bell System Technical Journal,1948,27(1):379-423.