平穩時序數據的Bootstrap辨識及其改進算法研究
黃雄波
(佛山職業技術學院 電子信息系, 佛山 528000)
0 引言
所謂時序數據,就是將某一物理量在不同時間上的實際觀測值,按照時間的先后順序排列而成的數列。 “平穩”是時序數據的重要特性,它描述了時序數據的數字統計特性是否隨著時間的推移而變化,通常,若時序數據的平均功率存在,其均值為常數,且自相關函數與起始時間無關,則稱該時序數據為廣義平穩時序數據或弱平穩時序數據,簡稱為平穩時序數據[1-2]。經過眾多專家學者的長期研究,平穩時序數據現已形成了一系列成熟可靠的辨識模型及建模方法,以自回歸模型(Auto-regressive model,AR)為例,該模型因結構簡單且具有高效的參數迭代估計算法,故在實際應用中得到了廣泛的應用[3-4]。然而,在現實生活中所獲取的時序數據普遍具有非平穩特性,又由于非平穩時序數據尚未有完整和統一的描述方法,據此,人們往往需要對其進行相關的平穩預處理[5-7]后,再采用平穩時序數據建模方法進行后續的辨識。例如,博克思(Box)和詹金斯(Jenkins)于上世紀70年代提出的自回歸積分滑動平均模型(Auto-regressive Integrated Moving Average Model,ARIMA),其核心就是通過有限次的差分處理,把原來的非平穩時序數據轉化為平穩時序數據[8];黃雄波基于自相關函數理論,對非平穩時序數據中的趨勢和周期成分的分離次序和方法作了系統而深入的研究,并得到了一種有效的平穩化轉換算法[9];王文華等基于貝葉斯框架對非平穩時序數據的分段平穩問題作了更為深刻的研究,并推導出具有遞歸關系的高效建模算法[10];張海勇等基于經驗模態分解法(Empirical mode decomposition, EMD)把待處理的非平穩時序數據分解成有限個基本的模式分量,然后分別為這些模式分量建立時變的AR模型,進而得到一種新的非平穩時序數據的自回歸模型分析方法[11-12]。
為了改善自回歸模型的辨識精度并給出相應的置信空間,近年來,國內外一些專家學者開始將Bootstrap方法應用到平穩時序數據的自回歸辨識過程中。例如,軒建平等基于小樣本統計的 Bootstrap 方法,對車削振顫自回歸模型參數的方差進行了估計,從而較好地解決了機床故障診斷中所需的大量樣本和重復多次試驗的難題[13];楊曉蓉等在單位根存在的條件下,證明了自回歸模型所構造的單位根檢驗統計量的極限分布,可以通過對最小二乘殘差進行Bootstrap重抽樣方法來逼近[14]。目前,基于Bootstrap方法的自回歸辨識算法在實際應用中還存在著一些問題,據此,本文擬設計相應的改進算法予以解決,并以相關的實驗來證明改進算法的有效性和先進性。
1 問題描述
時序數據辨識的過程就是對序列的數字統計特征及其分布的不確定性進行評價,在實際的辨識過程中,我們可以采用先驗知識、概率模型、可能性及置信區間等來求解不確定關系的表達式或者對其進行估計。然而,在大多數情況下,由于我們并不掌握待分析序列的總體分布,故很可能會得到錯誤的辨識結果。為克服因樣本數量不足而引起的分布估計誤差,一種有效的方法就是重抽樣,即通過某種模型對原序列進行反復采樣,使得原序列容量得到擴充,從而可以較為準確地估計某一統計量的標準差、均值及概率分布等。
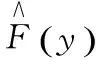
(1)
式(1)中,n為樣本長度,N(y)指時間y發生的總次數。
如圖1所示。
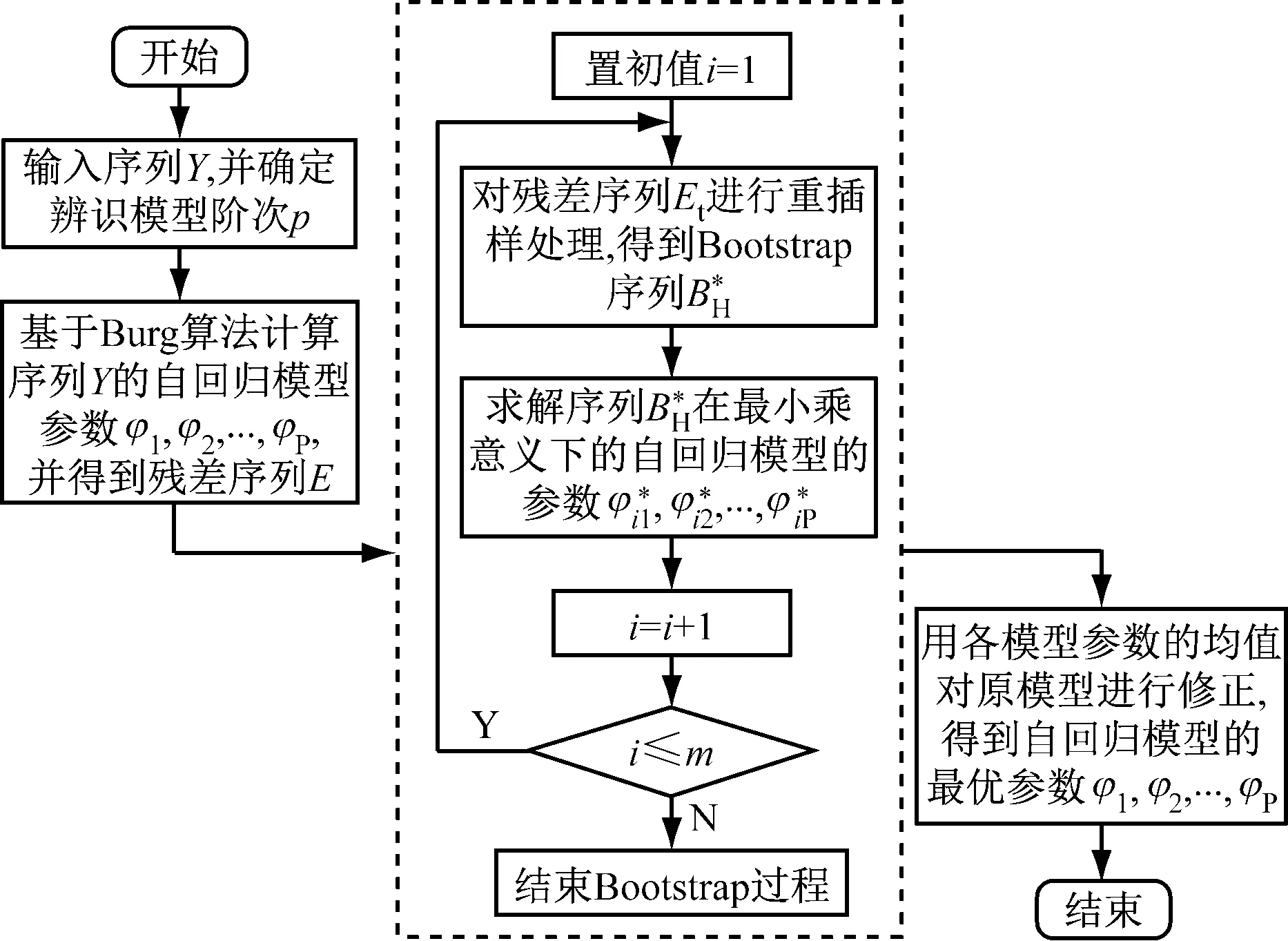
圖1 基于Bootstrap方法的自回歸辨識的算法流程圖
基于Bootstrap方法的自回歸辨識其核心思想就是對殘差序列進行m次重抽樣,然后構造出一系列的Bootstrap序列,通過對這些殘差序列進行參數估計,并用所得的參數均值來修正原有的自回歸模型。
2 改進算法的設計與實現
針對上述問題,本文擬對原有算法作如下改進:(1) 以自回歸模型的階數為Bootstrap的作用范圍區間,對殘差序列進行重抽樣處理;(2) 基于矩陣奇異值的迭代分解理論,對Bootstrap序列的參數進行求解。
2.1 改進的Bootstrap序列生成算法
在理想化的情形下,利用自回歸模型對平穩時序數據進行辨識,其剩余的殘差序列Et應為一白噪聲,即Et~N(0,σ2)成立。然而,由于數據污染和計算誤差等原因,殘差序列Et往往不能被白化,其各時刻之間的取值仍然存在著某種的統計關聯性。據此,在Bootstrap重抽樣的過程中,其作用范圍區間不應在整個序列內進行,而應以自回歸模型階數p作為滑動窗口的寬度,對殘差序列Et進行重抽樣,以便保持既有的相關性。根據上述的分析,可設計一種改進的Bootstrap序列生成算法。
算法1:保持既有相關性的Bootstrap序列生成算法
輸入:殘差序列Et,自回歸模型階數p;
步驟1:用Random()函數在1~n(n為序列的長度)中產生一個隨機整數R;
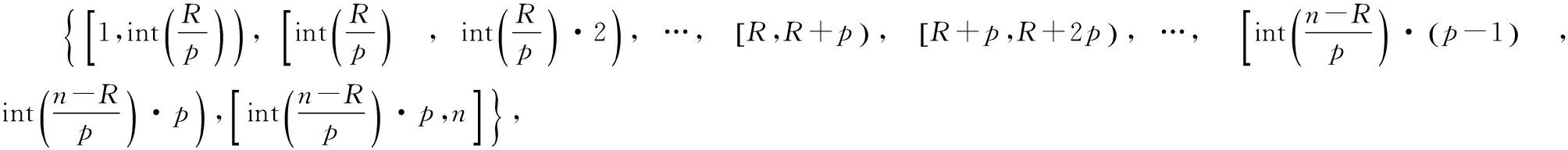
步驟3:應用Bootstrap方法獨立地對步驟2中的各個子空間中進行重抽樣處理;
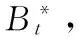
2.2 改進的Bootstrap序列估參算法
Bφ=b.
(2)
式(2)中,
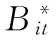
(3)
奇異值分解方法是最小二乘問題的有效求解方法,該方法的主要優點是處理病態和不相容線性方程組的能力強、運算過程中不放大誤差且具有良好的穩定性;而缺點就是運算量大。據此,這里擬引入矩陣奇異值分解方法對Bootstrap序列的自回歸模型參數進行求解,同時,為了克服運算量大的問題,還需要對奇異值分解方法進行如下的迭代計算改進。
設B(B∈R(n-1-p)×P,n>2p+1)的奇異值分解為式(4)。
(4)
其中,U=[u1,…,un-1-p]和V=[v1,…,vp]是正交矩陣,∑r=diag(σ1,…,σr),σ1≥…≥σr>0。根據矩陣Moore-Penrose廣義逆的定義,式(2)的最小二乘解為式(5)。
(5)
為了能使用迭代法對系數矩陣B進行奇異值分解,可以運用Householder變換求得正交矩陣U,V,從而實現系數矩陣B的二對角化,即式(6)。
(6)
其中,
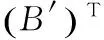
1) 初始化:
①k=1;
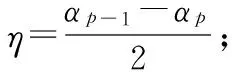
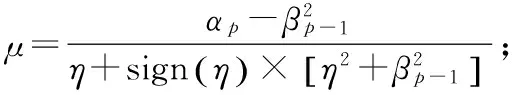
④c=α1-μ;
⑤d=β1;
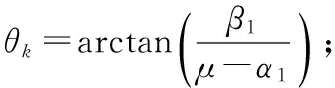
2) 求解如下的矩陣方程,得到奇異值σk:
3)k=k+1,求解如下的矩陣方程,更新θk:
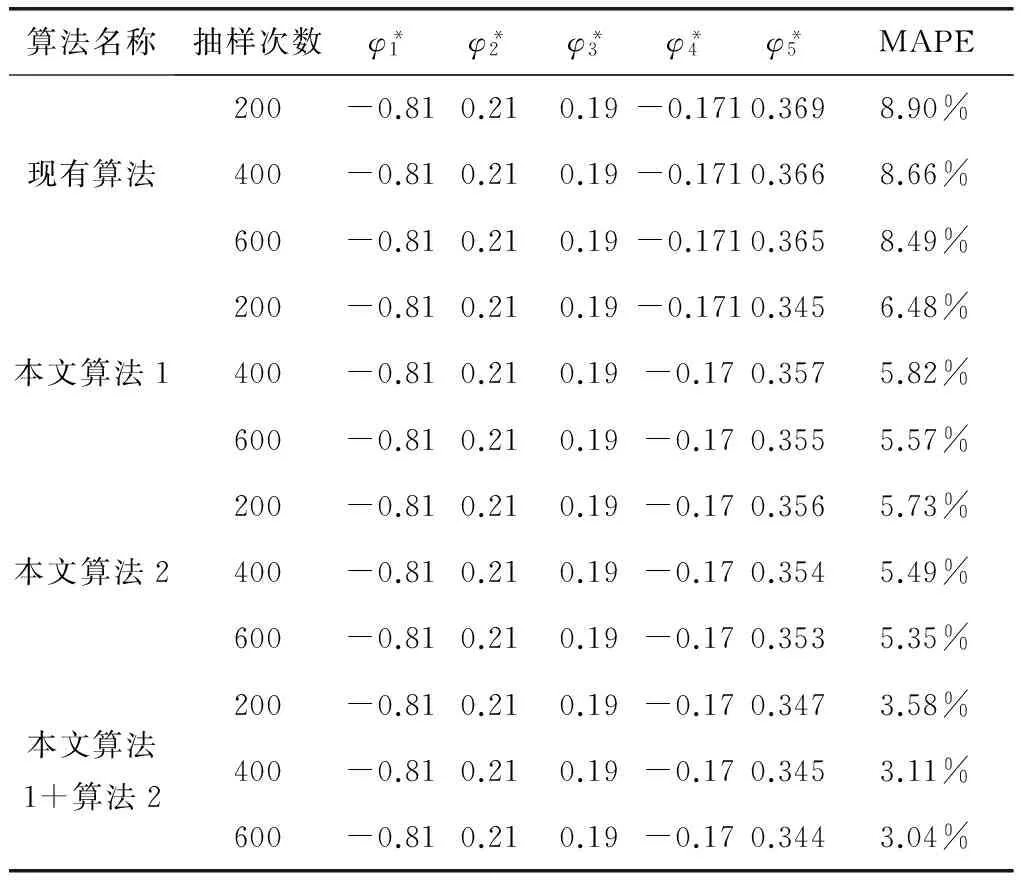
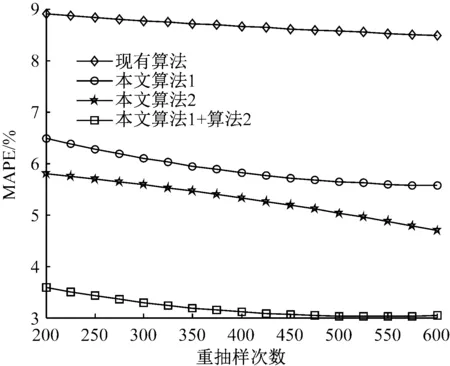
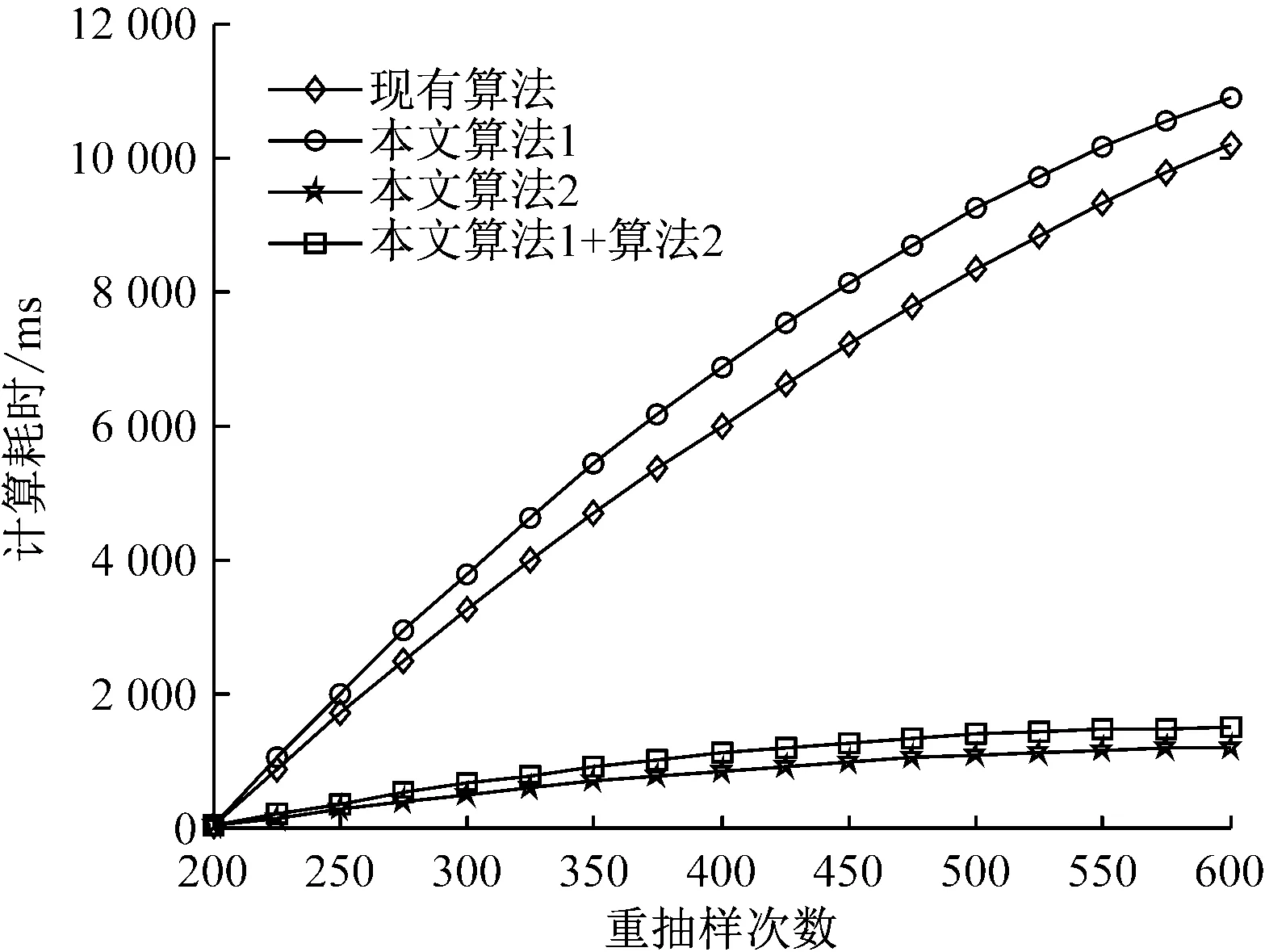
4) 若k 綜上所述,可設計如下的Bootstrap序列的估參改進算法。 算法2:基于奇異值迭代分解的Bootstrap序列估參算法 步驟2:對步驟(1)中的線性方程組的系數矩陣施行Householder變換,求得對應的正交矩陣U,V,把系數矩陣B化為式(6)所示的二對角化矩陣B′; 為了驗證上述改進算法的有效性及先進性,這里選取了一個自回歸仿真模型來進行相關的Bootstrap重抽樣辨識。實驗在PC機上進行,其硬件配置為,Intel 酷睿i5 4570四核CPU、Kingmax DDR3 16GB RAM、Western Digital 500G Hard Disk;操作系統與開發環境為,Microsoft Windows 10、Microsoft Visual Studio 2010集成開發環境中的C++。在實驗過程中,著重關注改進算法的辨識誤差和計算開銷等技術指標的改善情況,并對相關結果加以詳細的分析和討論。 實驗選用了一個五階的自回歸仿真模型,具體數學模型如式(7)。 yt=-0.81yt-1+0.21yt-2+0.19yt-3-0.17yt-4+0.33yt-5+zt. (7) 式(7)中,zt為服從標準高斯分布的白噪聲。 基于MATLAB軟件中,利用randn()隨機數發生函數和filter()數字濾波器函數為式(7)所示的模型生成長度為600的樣本序列。首先基于Burg算法對式(7)的模型進行辨識,然后分別應用現有的自回歸模型Bootstrap辨識算法、本文算法1、本文算法2及本文算法1+算法2對殘差序列進行辨識,并在{200,250,300,…,600}等不同抽樣次數的情形下,比對各種算法的辨識精度和辨識耗時的性能表現。 實驗過程中,為了客觀準確地評價各種算法的辨識精度,這里以式 (8)所示的平均絕對百分誤差(Mean absolute percent error, MAPE)作為評價指標,對各種實驗組合的辨識精度進行評價。如式(8)。 (8) 用Burg算法對式(7)所示的模型進行辨識,其結果如式(9)所示,于是,便可得到式(10)所示的殘差序列Et如式(9)、(10)。 (9) (10) 分別用現有算法、本文算法1、本文算法2及本文算法1+算法2對殘差序列Et進行自回歸辨識,取每次重抽樣其辨識參數的均值與式(9)中對應參數進行疊加求和,從而實現對原Burg算法辨識模型的修正。實驗所得的最終辨識參數如表1所示。 表1 各種算法所得的最終辨識參數 而各種算法的MAPE與重抽樣次數的關系則如圖2所示,限于篇幅,這里僅列出抽樣次數為200,400,600共3種情況。 圖2 各種算法的MAPE與重抽樣次數的關系 從表1可以發現,由于本文算法1在重抽樣的過程中保持了殘差序列之間既有的相關性,故其辨識精度較現有算法有了3%左右的提升;同樣地,基于奇異值迭代分解法的本文算法2因其數值計算更為精確,相應地,辨識精度較現有算法也有了一定的提升。而本文算法1+算法2則是融合了兩種改進算法的優點,在保持殘差序列之間既有相關性的同時,其估參過程中所產生的計算誤差也得到了較好的控制,故其對應的辨識精度也是最高的。如圖2所示。 MAPE與重抽樣次數之間的關系則表明,各種算法的重抽樣次數越多,其辨識精度也就越高,但當重抽樣次數達到序列長度的2/3 (400次)之后,辨識精度的提升效果便不再顯著,究其原因是因為此時的重抽樣操作已基本覆蓋了殘差序列的未知分布。 各種算法的計算耗時,如圖3所示。 圖3 各種算法的計算耗時 從圖3可以得知,本文算法1花費的計算耗時最多,現有算法次之,本文算法1+算法2排第三,而本文算法2則為最小。 以實驗中的模型為例,現有算法的每一次Bootstrap過程,均需要花費一定的時間進行重抽樣并生成Bootstrap序列,而且還需基于最小二乘法求解一個行數和列數分別為600和5的線性方程組,以便估算出對應的自回歸模型參數φ。實驗表明,現有算法的計算耗時主要是消耗在求解高度不相容線性方程組的過程中,據此,其計算耗時與重抽樣次數也就存在著明顯的線性關系。由于本文算法1的Bootstrap重抽樣過程較現有算法復雜,且自回歸模型參數φ的求解方法又與現有算法相同,故其計算耗時在略高于現有算法的同時又與其有著相同的特征。相對地,本文算法2基于奇異值迭代分解法改進了自回歸模型參數φ的求解過程,故其計算耗時有了大幅度的減少,并表現出對重抽樣次數具有良好的負載能力,即計算耗時不隨重抽樣次數的增加而顯著增加。而本文算法1+算法2的計算耗時在略高于本文算法2的同時,卻能保持著本文算法2的良好特性。 綜上所述,本文算法1+算法2在結合了兩種改進算法的基礎上,其計算精度和計算耗時均較現有算法有了顯著的提升。 對現有的基于Bootstrap方法的自回歸模型辨識算法, 進行了兩點有意義的改進,改進后的算法具有更優異的辨識性能指標。下一步的主要工作有,研究更為合理的Bootstrap重抽樣約束機制,同時,也需要研究并行的奇異值迭代分解法,以便進一步提升算法的適用范圍和計算性能。 [1] 克西蓋斯納,沃特斯,哈斯勒.現代時間序列分析導論[M].張延群,劉曉飛,譯.北京:中國人民大學出版社,2015. [2] 冀振元.時間序列分析與現代譜估計[M].哈爾濱:哈爾濱工業大學出版社,2016. [3] 黃雄波,胡永健.利用自回歸模型的平穩時序數據快速辨識算法[J/OL,網絡優先出版].計算機應用研究,2018,35(9). [4] 蘇志銘,陳靚影.基于自回歸模型的動態表情識別[J]. 計算機輔助設計與圖形學學報,2017, 29(6):1085-1092. [5] 王宏禹,邱天爽,陳喆.非平穩隨機信號分析與處理(第2版)[M]. 北京:國防工業出版社,2008. [6] 王宏禹,邱天爽.非平穩確定性信號與非平穩隨機信號統一分類法的探討[J]. 通信學報,2015, 36(2):2801-2810. [7] 王宏禹,邱天爽.確定性信號分解與平穩隨機信號分解的統一研究[J]. 通信學報,2016, 37(10):1891-1898. [8] 博克思,詹金斯,萊因澤爾.時間序列分析:預測與控制(第4版)[M].王成璋譯.北京:機械工業出版社,2011. [9] 黃雄波.基于自相關函數的非平穩時序數據的辨識改進[J]. 微型機與應用,2016, 35(13):10-14. [10] 王文華,王宏禹.分段平穩隨機過程的參數估計方法[J]. 電子科學學刊,1997, 19(3):311-317. [11] 張海勇,馬孝江,蓋強.一種新的時變參數AR模型分析方法[J]. 大連理工大學學報,2002, 42(2):238-241. [12] 張海勇,李勘.非平穩隨機信號的參數模型分析方法[J]. 系統工程與電子技術,2003, 25(3):386-390. [13] 軒建平,史鐵林,楊叔子. AR模型參數的Bootstrap方差估計[J]. 華中科技大學學報,2001, 29(9):81-83. [14] 楊曉蓉.自回歸時間序列的極限理論及其應用[D].浙江大學博士學位論文,2008. [15] 徐禮文.復雜數據的bootstrap統計推斷及其應用[M].北京:科學出版社,2016. [16] James W.Demmel.應用數值線性代數[M] 王國榮譯.北京:人民郵電出版社,2007. [17] 徐樹方.數值線性代數(第二版)[M].北京:北京大學出版社,2013.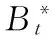
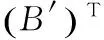
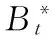
3 實驗及結果分析
3.1 實驗過程與方法
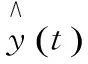
3.2 實驗的結果與分析
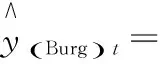
4 總結

