前緣直板擾流對高速空腔的降噪效果分析

周方奇，楊黨國,*，王顯圣，劉俊，施傲

1.中國空氣動力研究與發展中心 空氣動力學國家重點實驗室，綿陽 621000 2.中國空氣動力研究與發展中心 高速空氣動力研究所，綿陽 621000

空腔流動普遍存在于航空航天領域。高速氣流流經空腔，當滿足一定的空氣動力學和幾何條件時，腔內流動會產生劇烈的壓力脈動并誘發高強度噪聲，不僅對空腔流場結構影響較大，而且還威脅腔內設備和空腔自身結構安全。因此針對空腔噪聲的抑制研究一直受到廣泛關注[1-7]，其中前緣擾流流動控制是一種簡單有效的噪聲抑制方法。Stanek等[8]研究了前緣鋸齒、橫向圓柱和繞有細鐵絲的圓柱桿等擾流裝置對腔內流動和噪聲的影響。Schmit等[9-11]利用高速攝影技術研究了超聲速條件下前緣直板、圓柱和鋸齒對腔內流動和噪聲的影響，發現前緣擾流裝置可以通過抬高剪切層的位置削減進入空腔的流量，從而抑制空腔高強度噪聲。Thangamani等[12-14]研究了前緣鋸齒對空腔噪聲抑制效果，指出前緣鋸齒可以改變空腔上方剪切層的三維形態和高度并破壞其連續性。Panickar和Raman[15-16]研究了前緣圓柱對空腔噪聲和自持振蕩的影響，指出前緣圓柱可以在較大的速度范圍內抑制腔內噪聲。Dudley和Ukeiley[17-19]發現前緣圓柱可以使剪切層向腔外偏轉，從而抬高剪切層的位置并增加其厚度和穩定性，有效減弱與后壁相撞的沖擊。國內研究人員也通過在空腔前緣添加鋸齒和吹吸氣裝置等方式，開展了空腔噪聲控制研究[20-22]。國內外對空腔流動/噪聲的控制研究大多集中在亞聲速來流條件下，且關注的重點是對噪聲控制效果的分析，而對超聲速條件下結合空腔壁面和空間流譜結構的空腔流動/噪聲控制研究機理探討較少。

本文以某型號飛機的工程具體應用為研究背景，通過對比多種不同控制參數狀態下腔內的噪聲聲壓級分布，確定前緣直板控制參數的優化選擇方法和最優控制參數；綜合利用風洞試驗測量腔內靜態/動態壓力、腔壁面油流圖譜和流場結構拓撲圖，深入分析了跨超聲速條件下具有代表性的優選出的典型前緣直板對腔內流動/噪聲的控制機理、效果和影響規律，為建立具有工程實用價值的控制對策提供理論支撐和方法借鑒。

1 風洞試驗

1.1 試驗設備

試驗在中國空氣動力研究與發展中心高速所的FL-21風洞中完成。FL-21風洞系橫截面為 0.6 m×0.6 m半回流暫沖式亞、跨、超三聲速風洞，試驗馬赫數范圍為0.2～3.5，試驗段長度為 1.775 m。跨聲速時試驗段上下為槽壁，兩側為實壁，超聲速時四壁均為實壁。

利用美國Kulite公司型號為XCE-062的壓阻式傳感器測量腔內脈動壓力，其量程為30 PSI (1 PSI=6.895 kPa)，固有頻率為200 kHz，試驗中傳感器采樣頻率設置為50 kHz。腔內靜壓則通過PSI 9016電子掃描閥系統進行測量，其量程為15 PSI，測量精度達到±0.05% FS (Full Scale)，采樣率為每通道100 Hz。

1.2 試驗模型

試驗模型總長為514 mm，寬為320 mm，腔體的長度L為200 mm，深度D為33.3 mm，寬度W為66.7 mm，長深比為6，寬深比為2。空腔流動控制模型實物如圖1所示。

為開展不同類型的試驗研究，分別加工了“測壓腔”和“油流腔”兩種腔體。“測壓腔”底部和前壁中軸線上交替分布有脈動壓力和靜壓測點，腔內壓力傳感器分布如圖2所示，其中：x/L為流向坐標與空腔長度的比值。由于模型還需完成后緣修型等其他控制方法的試驗研究，有些控制裝置需通過空腔后壁的螺孔進行安裝，因而后壁面并未布置傳感器測點。“油流腔”內部為光滑的金屬表面，為了增強油流的對比度，通過電化學的方法使腔體表面黑化(見圖1)。

圖1 空腔流動控制模型Fig.1 Cavity flow controlling model

圖2 腔內壓力傳感器分布Fig.2 Distoribution of pressure sensors in cavity

圖3 空腔前緣處的直板結構Fig.3 Plate structure at leading edge of cavity

空腔前緣設有卡槽用以安裝前緣直板擾流裝置，與模型前緣之間為200 mm的光滑平板，來流在其上發展形成湍流邊界層，并在空腔前緣與直板控制裝置相互作用。前緣直板的幾何形狀通過3個參數確定，分別為展度e、傾斜角度θ和底縫開度h(如圖3所示)。來流邊界層形態和厚度δ是影響空腔上方剪切層形成、發展和渦脫落頻度的一個關鍵參數，對空腔的流動特征有著重要影響，因而對空腔內的多尺度湍流結構和噪聲的控制對策一定要考慮邊界層的模擬和影響。為此，依據空腔流動尺度影響和控制技術構建思路，引入前緣直板控制參數e*和h*，分別定義為e*=e/δ，h*=h/δ，代表了前緣直板裝置展度e和底縫開度h與空腔前緣來流邊界層厚度δ之比，可有效反映空腔前緣直板控制裝置尺度與邊界層厚度的相對關系以及控制對策的特征參數，指導真實環境和條件下控制措施的構建。

2 數據處理

通過脈動壓力傳感器采集到的時域信號中包含直流和交流2種成分，經過濾波處理去除直流成分，保留交流成分p(t)，其均方根計算式為

(1)

式中：T為樣本長度。從而獲取脈動壓力時域樣本的聲壓級SPL為

(2)

式中：pref=2.0×10-5Pa為參考壓力。樣本的聲壓級反映了測點處流場中壓力脈動的強度，可以有效描述腔內噪聲的分布狀況。

利用MATLAB軟件函數庫中的Pwelch函數計算時域脈動壓力樣本的功率譜密度PSD，然后通過式(3)獲取樣本的聲壓頻譜SPFS，從而對腔內噪聲進行頻譜分析。

(3)

3 控制參數的影響及優化選擇

試驗中共準備了9種不同控制參數的前緣直板裝置，在Ma=0.9和Ma=1.5來流條件下分別開展空腔流動控制試驗。根據腔內噪聲分布，對比分析展度e、傾斜角度θ和底縫開度h共3種控制參數對控制效果的影響，并確定試驗中最優的控制參數和優化選擇方法。通過前期的邊界層特性測量試驗，獲取了Ma=0.9和Ma=1.5兩種來流條件下空腔前緣處的邊界層厚度δ分別為3.3 mm和3.4 mm。利用邊界層厚度δ的試驗結果和直板的幾何尺寸，可以確定Ma=0.9和Ma=1.5來流條件下直板的控制參數e*和h*。

3.1 直板展度的影響

通過對比不同展度前緣直板控制條件下腔內的聲壓級分布，分析直板展度e對腔內噪聲的影響。圖4給出了4種不同展度的直板控制條件下腔內壁面中心線上的聲壓級分布曲線，其中直板的傾角均為45°，底縫開度均為0 mm，展度依次為2.2、3.3、4.4和5.5 mm，具體的參數見表1。通過圖4中聲壓級曲線的對比可以看出：在傾角和底縫開度不變的情況下，隨著直板展度的增加，腔內聲壓級逐漸降低，其中Ma=0.9時聲壓級的變化主要集中在空腔的兩端，中段變化相對微弱；Ma=1.5時則表現為聲壓級曲線整體向下平移。另外，直板展度從2.2 mm增加至3.3 mm時聲壓級下降的幅度最大，在后緣測點處Ma=0.9和Ma=1.5時分別達1.3 dB和1.2 dB，展度繼續增加后聲壓級降低的幅值逐漸減小。上述現象表明：當e<3.3 mm，e*<1.0時，即前緣直板的展度小于來流邊界層厚度時，腔內噪聲對展度的變化較敏感，直板展度的增加對噪聲抑制具有較強的效果；當展度大于邊界層厚度時，腔內噪聲對展度的敏感性逐漸減弱。

圖4 不同展度的直板控制條件下腔內聲壓級分布Fig.4 Distribution of sound pressure level in cavity for controlling with plates of different extents

表1 不同展度直板的具體參數Table 1 Parameters of plates with different extents

Platee/mmθ/(°)h/mme*Ma=0.9Ma=1.5Plate-12.24500.670.64Plate-23.34501.000.97Plate-34.44501.331.29Plate-45.54501.671.62

直板展度的增加雖然可以降低腔內噪聲，但同時也會增大直板在來流法向上的投影面積，導致空腔附近阻力的提升，進而影響飛行器的整機氣動特性和飛行性能。因而結合噪聲抑制效果和氣動特性需求，前緣直板的展度與邊界層厚度相當(本試驗中為3.3 mm左右)時應用價值最大。

3.2 直板傾角的影響

直板的傾角主要是依據超聲速來流條件下空腔前緣產生的典型流動特征(如膨脹波或激波等)的傾斜角度來確定的。通過對比不同傾角前緣直板條件下腔內的聲壓級分布，分析直板傾角對腔內噪聲的影響。圖5給出了3種不同傾角的直板控制條件下腔內的聲壓級分布曲線，其中直板的展度均為3.3 mm，與來流邊界層厚度基本相當，底縫開度均為0 mm，傾角θ依次為30°、45°和60°，具體的參數見表2。從圖5中不同曲線間的對比可以看出：在直板展度和底縫開度不變的情況下，當傾角從30°增長到45°時，Ma=0.9條件下后緣附近聲壓級顯著下降，Ma=1.5條件下聲壓級曲線整體向下平移；當傾角從45°增大到60°，Ma=0.9條件下大部分區域聲壓級變化微弱，而Ma=1.5條件下兩條聲壓級曲線幾乎重合。上述現象表明：當前緣直板的傾角θ<45°時，腔內噪聲對直板傾角的變化比較敏感，傾角的增加有利于對腔內噪聲的抑制；當傾角θ>45°時，繼續增大傾角對腔內噪聲影響微弱。另外，傾角的增大也會增加直板在來流法向上的投影面積，提高空腔附近的阻力，因而綜合考慮噪聲抑制和氣動特性需求，空腔前緣直板控制的最優傾角為45°。

圖5 不同傾角的直板控制條件下腔內聲壓級分布Fig.5 Distribution of sound pressure level in cavity for controlling with plates of different angles

表2 不同傾角直板的具體參數Table 2 Parameters of plates with different angles

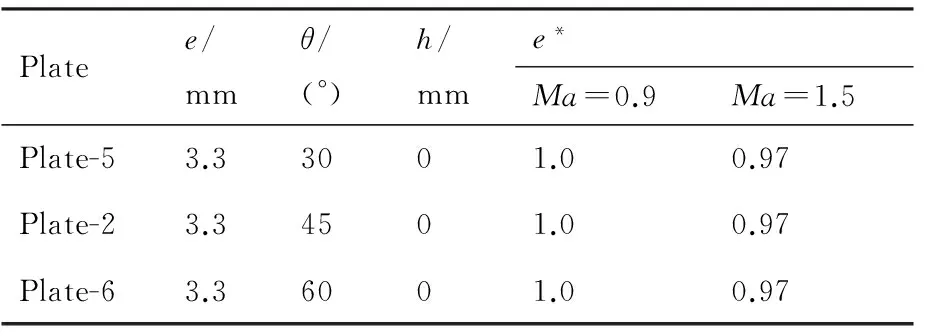
Platee/mmθ/(°)h/mme*Ma=0.9Ma=1.5Plate-53.33001.00.97Plate-23.34501.00.97Plate-63.36001.00.97

3.3 直板底縫開度的影響

通過對比不同底縫開度前緣直板條件下腔內的聲壓級分布，分析直板底縫對腔內噪聲的影響。圖6給出了4種不同底縫開度的直板控制條件下腔內聲壓級分布，4種直板的展度均為3.3 mm，傾角θ均為45°，底縫開度依次為0、0.5、1.0和1.5 mm，具體參數見表3。從圖6中可以看出：當直板展度和傾角不變時，隨著直板底縫開度的增加，除Ma=0.9條件下個別測點外，腔內聲壓級均逐漸減小。通過聲壓級曲線的變化趨勢可以發現：當h<1 mm，h*<0.3時，腔內聲壓級對底縫開度的變化較敏感，隨著底縫開度的增加，后部聲壓級顯著下降，底縫開度h從0.5 mm增加到1.0 mm時，Ma=0.9和Ma=1.5條件下后緣聲壓級降低幅值均達到0.7 dB以上；當h>1 mm，h*>0.3時，雖然噪聲對開度的敏感性減弱，增加底縫開度仍然可以使得聲壓級繼續下降。上述現象表明在試驗提供的底縫開度變化范圍內，即h≤1.5 mm條件下，通過在前緣直板的底部增加底縫可以增強對腔內噪聲的抑制，底縫開度的增大可以提升噪聲的抑制效果。另外，由于底縫開度變化的過程中直板在來流法向上的投影面積保持不變，對飛行器的氣動特性影響較小。因而增加底縫開度有利于直板對空腔噪聲的抑制，試驗提供的底縫開度最大值h=1.5 mm為最優底縫開度。

圖6 不同底縫開度直板控制條件下腔內聲壓級分布Fig.6 Distribution of sound pressure level in cavity for controlling with plates of different crack sizes

表3 不同底縫開度直板的具體參數Table 3 Parameters of plates with different crack sizes

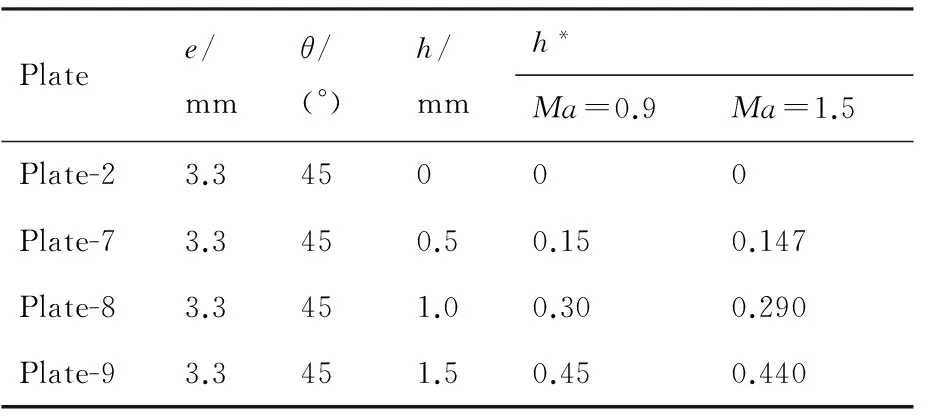
Platee/mmθ/(°)h/mmh*Ma=0.9Ma=1.5Plate-23.345000Plate-73.3450.50.150.147Plate-83.3451.00.300.290Plate-93.3451.50.450.440

通過以上9種前緣直板控制條件下腔內聲壓級的分類對比，分別對前緣直板的展度、傾角和底縫開度3個控制參數進行了優化選擇，并確定了試驗中的最優控制參數：展度e=3.3 mm，傾角θ=45°，底縫開度h=1.5 mm。而前緣直板Plate-9的展度、傾角和底縫開度均與3種最優控制參數相符，同時在其作用下腔內聲壓級也低于其他流動控制狀態，因而第4節將以直板Plate-9為研究對象，對前緣直板流動控制條件下腔內的流場和噪聲進行深入分析。

4 典型前緣直板控制效果分析

開展Ma=0.9和Ma=1.5來流條件下的風洞試驗，根據無流動控制的基準狀態及前緣直板Plate-9流動控制狀態下腔內靜態/動態壓力測量和壁面油流試驗結果，分析前緣直板Plate-9對腔內流場和噪聲特性的影響規律和控制機理。

4.1 靜壓分布

利用壁面的靜壓測點可以獲取不同來流條件下腔內流場的靜壓分布，基準狀態和前緣直板Plate-9流動控制狀態下腔內底面中軸線上無量綱靜壓系數Cp的分布曲線如圖7所示，從中可以看出：無論在Ma=0.9還是Ma=1.5來流條件下，基準狀態時Cp曲線均呈明顯的3段式擬線性分布，因此可以根據該特征將腔內流場沿流向劃分為3個區域：Ⅰ區域x/L∈(0,0.43)、Ⅱ區域x/L∈[0.43,0.85)和Ⅲ區域x/L∈[0.85，1.00)，并從以上3個區域分別分析前緣直板對腔內靜壓的影響。

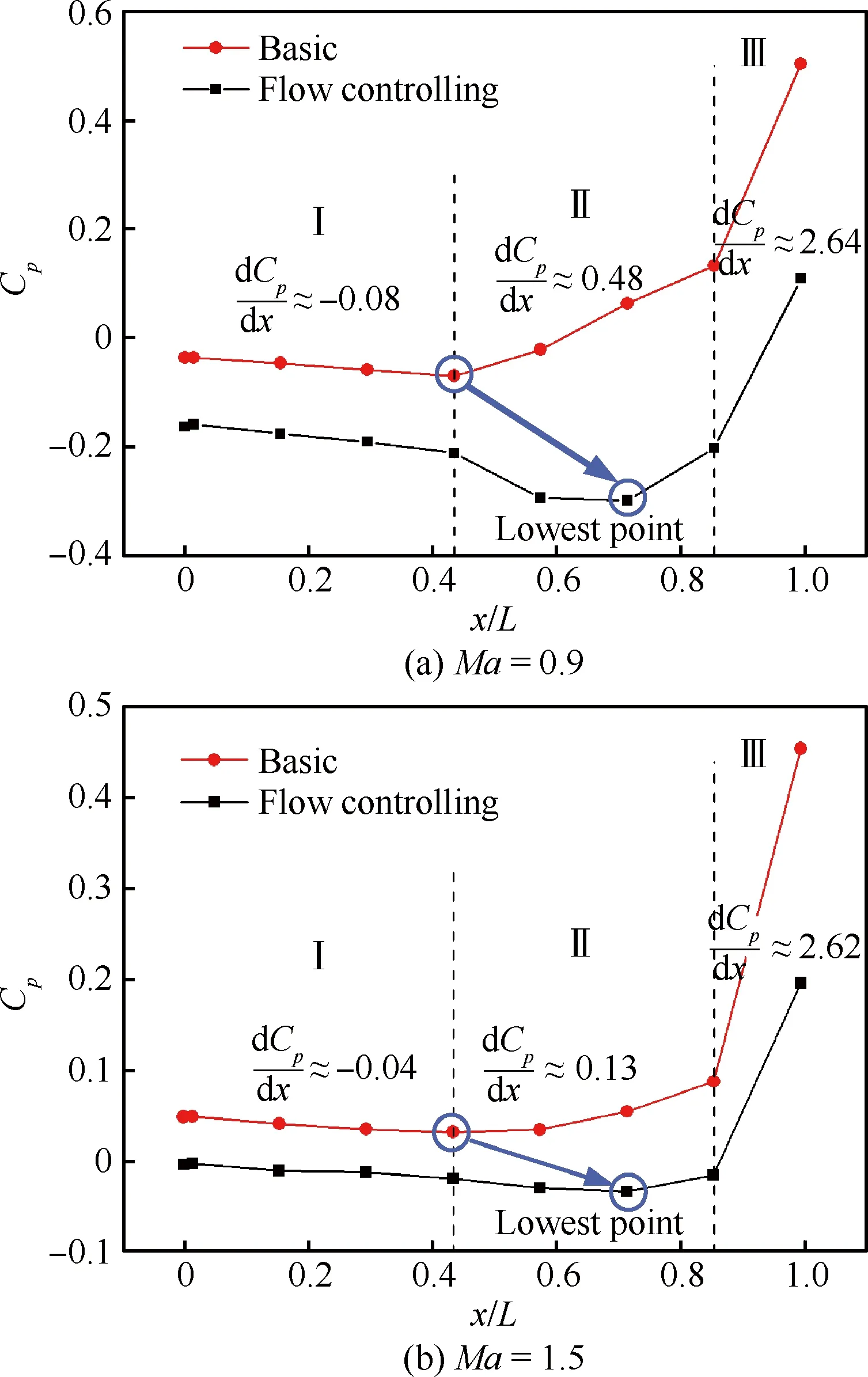
圖7 基準狀態和Plate-9流動控制條件下腔內 無量綱靜壓分布 Fig.7 Distribution of dimensionless static pressure in cavity under basic and Plate-9 flow controlling conditions

對比基準狀態和流動控制狀態下的Cp曲線，發現在空腔前緣安裝直板Plate-9后，腔內3個區域靜壓系數均有所下降，其中：Ⅲ區域中的變化最為顯著，Ma=0.9和Ma=1.5條件下后緣附近Cp分別降低0.394和0.258；而Ⅰ區域中控制效果相對較弱，表現為曲線整體向下平移，Ma=0.9和Ma=1.5時分別下移幅度約0.1和0.05左右。另外，前緣直板還改變了Ⅱ區域中靜壓的發展趨勢，使得壓力最低點的位置發生變化，不同來流條件下腔內靜壓的最低點均由基準狀態時的x/L=0.42附近移至x/L=0.71，同時Ⅱ區域中Cp曲線變化趨勢也隨之改變，由基準狀態時的線性增加，轉變為先減小后增大。腔內靜壓的變化狀況說明前緣直板流動控制主要對Ⅲ區域中產生較大作用，并引起Ⅱ區域流場結構的改變，而對前部Ⅰ區域影響相對較弱。

4.2 油流圖譜

油流圖譜代表了壁面的摩擦力線分布情況，可以有效反映流體在壁面的分離和附著特征，以及附近流場結構，因而通過對比前緣直板Plate-9流動控制前后空腔壁面流譜，可以進一步分析前緣直板對腔內流場的影響。圖8和圖9分別給出了Ma=0.9和Ma=1.5來流條件下基準狀態和流動控制狀態腔內各壁面的油流圖譜照片。

側壁照片中空腔上緣處的橫向軌跡反映了剪切層的發展狀況。從圖8(a)和圖9(a)中可以看出：Ma=0.9和Ma=1.5時，基準狀態條件下剪切層均從前緣附近產生并沿空腔上緣向后運動，在此過程中其厚度逐漸增長并向腔內延伸，其中亞聲速條件下剪切層厚度的增長率高于超聲速。而流動控制狀態下，空腔側壁上緣附近基本無橫向軌跡，流譜主要呈縱向分布，與基準狀態時的表現差異較大，這是由于前緣傾斜的直板裝置不僅抬高了剪切層分離點的位置，同時增強了流體向腔外的速度分量，導致剪切層的運動高度大幅度上升并從腔外掠過，因而側壁的流譜中難以觀察到其流動軌跡。

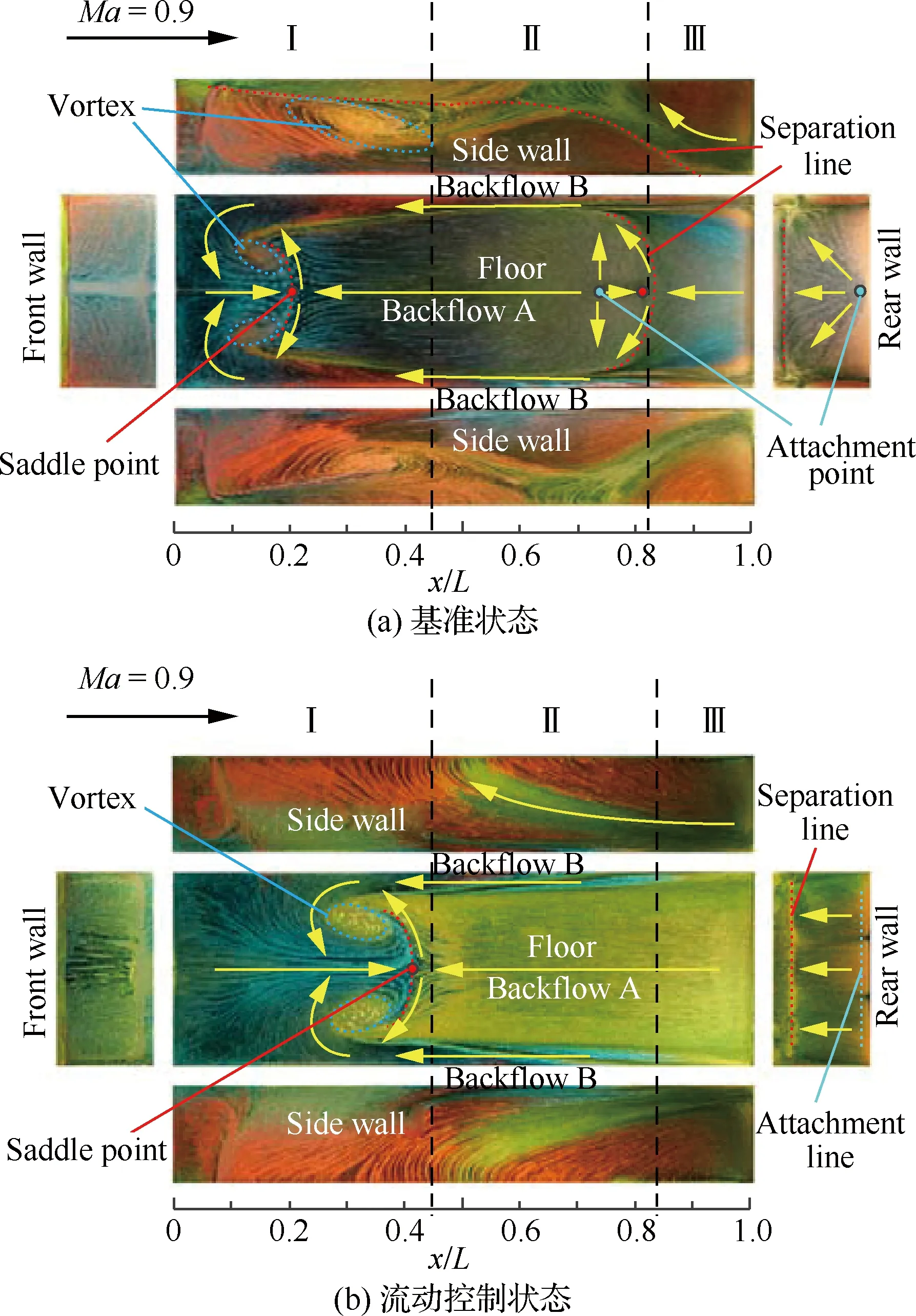
圖8 Ma=0.9時基準狀態和直板Plate-9流動 控制條件下空腔壁面油流圖譜 Fig.8 Oil flow patterns on cavity surfaces under basic condition and Plate-9 flow controlling conditions at Ma=0.9

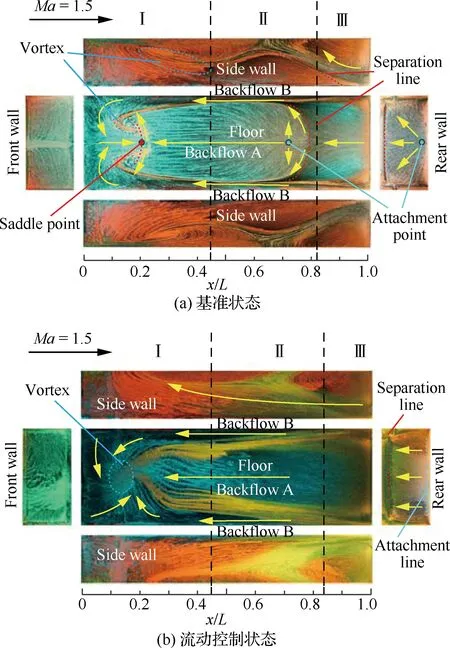
圖9 Ma=1.5時基準狀態和直板Plate-9流動 控制條件下空腔壁面油流圖譜 Fig.9 Oil flow patterns on cavity surfaces under basic condition and Plate-9 flow controlling conditions at Ma=1.5

剪切層的抬升導致流體對后緣的撞擊位置發生改變。基準狀態下剪切層沿流向運動過程中，在到達后壁之前已接觸底面，圖8(a)和圖9(a)中底面和后壁上附著點的位置說明流向流體撞擊范圍從底面后部延伸至后壁。而在流動控制狀態下，由于剪切層位置的上升以及向腔外速度分量的增加，流體的橫向運動距離增大，在后緣的撞擊位置也向后推移，從圖8(b)和圖9(b)可以看出流體在后緣的附著區域主要集中在空腔后壁面，與基準狀態相比流體的撞擊范圍顯著縮小，從而進入腔內的流量也隨之減少。

撞擊空腔后緣后，流體沿底面向前回流。根據底面流譜中橫向軌跡的顏色，可將回流分為兩部分：回流A沿底面中軸線向前運動，直至Ⅰ區域中的分離線，其流動軌跡集中在底面中軸線及其兩側；回流B則沿兩側壁向前緣流動，在Ⅰ區域中撞擊前壁后改變方向，向底面中軸線匯聚同時轉為沿流向流動。通過Ⅱ區域底面照片可以看出回流A流譜軌跡的截面寬度遠大于回流B，說明回流A的流量遠多于回流B，為腔內的主要回流。

Ma=0.9來流條件下，兩部分回流在Ⅰ區域相撞并發生流動分離，底面圖譜中可以清晰地看見兩者交匯形成的鞍點、分離線以及沿中軸線對稱的兩個旋渦分離點。基準狀態下剪切層在后緣的撞擊范圍較大，底面回流強度也較高，回流A的流量遠多于回流B，因而Ⅰ區域中兩部分流體相撞產生的鞍點和分離線的位置趨于前壁，位于x/L=0.2左右(見圖8(a))。而在流動控制狀態下，從后緣進入腔內的流量減少，導致回流A的強度顯著下降，因而底面鞍點和分離線向右移動，從x/L=0.2右移至x/L=0.4附近(見圖8(b))。

Ma=1.5時，基準狀態條件下空腔底面油流圖譜與Ma=0.9時類似(見圖9(a))，流動控制狀態下，Ⅰ區域中沿中軸線對稱的分離線和兩個旋渦分離點被一個旋渦分離點取代(見圖9(b))，回流A和回流B共同匯入該分離點，使得底面流譜表現出一定的非對稱性。超聲速條件下來流的非穩定性較強，而前緣直板又進一步放大了流動的非穩定性，從而引起兩側回流B的失衡，在前壁附近匯聚的過程中偏離了中軸線，因而在Ⅰ區域與回流A的撞擊并不充分，兩者在交匯過程中形成一個距離前壁較近的旋渦分離點。

4.3 流場結構

根據油流圖譜中底面流動分離和附著的位置以及側壁旋渦的形態定性描繪了Ma=0.9和Ma=1.5條件下腔內中軸面上的流場結構，如圖10和圖11所示。

基準狀態下剪切層在發展過程中厚度逐漸增加，最終撞擊空腔底面和后壁，形成后緣高壓和沿底面向前的回流，以及橫跨Ⅰ和Ⅱ區域的主回流旋渦(圖8(a)和圖9(a)底面照片中Ⅰ區域的分離線反映了回流區的范圍)；流動控制狀態下，前緣直板有效地抬高了剪切層，增加了其流向的運動距離，使得部分流體直接跨過空腔，從而降低了流體進入腔內的流量，以及對后緣的撞擊強度。

圖10 Ma=0.9時腔內流向中軸面流場結構Fig.10 Flow configuration on axis surface of cavity at Ma=0.9

圖11 Ma=1.5時腔內流向中軸面流場結構Fig.11 Flow configuration on axis surface of cavity at Ma=1.5

通過對剪切層的抬高作用，前緣直板不僅降低了腔內靜壓和后緣逆壓梯度(見圖7)，同時削弱了腔內回流的強度，抑制了回流區的范圍。Ma=0.9時底面Ⅰ區域的分離線在前緣直板的作用下從x/L=0.2附近移動至x/L=0.4(見圖8)，反映了主回流旋渦的后移。另外，主旋渦中心壓力較低，在Ⅱ區域的流場中形成壓力最低點，而隨著主回流旋渦的后移，底面靜壓最低點的位置也隨之向右移動，圖7中壓力最低點位置與圖10和圖11中主回流旋渦中心保持一致。

4.4 腔內聲壓級

腔內的復雜流動會產生劇烈的壓力脈動，從而形成高強度噪聲，利用脈動壓力傳感器的測量結果，對腔內噪聲的分布特性進行分析。圖12給出了Ma=0.9和Ma=1.5來流條件下腔內總聲壓級的分布曲線，可以看出基準狀態下腔內聲壓級沿流向均成波浪式上升分布，并在空腔后緣分別達到最大值172.27 dB和172.13 dB。

圖12 基準狀態和直板Plate-9流動控制條件下 腔內聲壓級分布曲線 Fig.12 Curves of sound pressure level in cavity under basic conditions and Plate-9 flow controlling conditions

在空腔前緣安裝直板Plate-9后，腔內噪聲得到有效抑制，尤其在空腔中后部分聲壓級顯著下降，Ma=0.9和Ma=1.5來流條件下后緣附近聲壓級降低幅值分別達11.13 dB和8.0 dB。在前緣直板流動控制條件下，剪切層被大幅度抬高，有效減弱了流體撞擊后緣時的強度和流量，從而抑制了后緣高強度噪聲的產生。

4.5 聲壓頻譜

空腔后緣附近聲壓級最強，且前緣直板Plate-9對后緣處噪聲的抑制效果也十分顯著，因此通過后緣測點的聲壓頻譜進一步分析腔內噪聲的特性。圖13對比了基準狀態和流動控制狀態下后緣附近x/L=0.92處的聲壓頻譜。根據頻譜曲線的峰值確定腔內噪聲的模態頻率，并利用藍色虛線在圖13中對其位置進行了標注，可以看出在Ma=0.9和Ma=1.5條件下基準狀態和流動控制時峰值位置保持一致，說明前緣直板對腔內噪聲的模態頻率基本無影響。

圖13 空腔后緣附近測點處的聲壓頻譜Fig.13 Sound pressure level spectra of aft edge in cavity

在空腔前緣安裝直板Plate-9之后，無論是亞聲速還是超聲速條件下，聲壓頻譜曲線顯著向下平移，寬頻噪聲和峰值噪聲都受到顯著影響。在前緣直板的作用下，寬頻噪聲在低頻范圍內(小于1 000 Hz)受到明顯的抑制，該效果隨著頻率的增加逐漸減弱；同時，腔內峰值噪聲的幅值也大幅度降低，尤其是最高峰值(二階模態峰值)，在Ma=0.9和Ma=1.5來流條件下分別下降了19.4 dB和22.5 dB。

圖14 基準狀態和直板Plate-9流動條件下腔內 二階模態噪聲空間分布曲線 Fig.14 Curves of spatial distribution of the second mode noise in cavity under basic and Plate-9 flow controlling conditions

為進一步分析前緣直板對腔內峰值噪聲的影響，圖14給出了不同Ma條件下腔內二階模態峰值噪聲幅值在底面的分布曲線。基準狀態條件下峰值噪聲在腔內呈波浪式分布，而在前緣安裝直板Plate-9之后，峰值噪聲的幅值曲線整體向下平移，Ma=0.9和Ma=1.5時分別降低11 dB和20 dB以上，表明前緣直板對峰值噪聲的抑制效果在整個空腔內均十分顯著。峰值噪聲產生于剪切層中非定常運動對后緣的周期性撞擊，并以壓力波的形式在腔內傳播。由于前后壁面的多次反射，壓力波在腔內疊加形成駐波，因而其幅值在空間上呈波浪式分布。前緣直板抬高了剪切層的高度，并削弱了其對后緣的撞擊作用，從聲源上抑制了峰值噪聲的產生，減小了腔內壓力波的強度和駐波的幅值，從而使得峰值噪聲的幅值在整個腔內大幅度下降。

5 結 論

1) 在前緣直板的作用下，剪切層的位置大幅度抬高，導致與腔后緣的撞擊位置顯著后移，從而削弱流體進入空腔的流量及對后緣的撞擊強度。

2) 前緣直板通過減少進入腔內的流量降低了腔內靜壓和前后緣的壓差，抑制了回流的強度和范圍，并導致回流旋渦和靜壓低點向下游移動。

3) 前緣直板通過削弱剪切層對后緣的撞擊強度，有效降低了空腔后壁處的噪聲源強度，進而實現了空腔內聲壓級的控制，不僅使激振頻率處的峰值噪聲大幅度下降，還使寬頻噪聲也受到明顯抑制。

[1] FLAHERTY W, REEDY T M, GREGORY S, et al. Investigation of cavity flow using fast-response pressure sensitive paint[C]∥51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Reston, VA: AIAA, 2013: 1-15.

[2] THIEMANN C L, MILNE G J, VAKILI A D. An experimental investigation of supersonic cavity flow control with vertical cylinders[C]∥43rd Fluid Dynamics Conference. Reston, VA: AIAA, 2013: 1-13.

[3] GUPTA A D, ROY S. Noise control of cavity flows for subsonic receptive channels[C]∥53rd AIAA Aerospace Sciences Meeting. Reston, VA: AIAA, 2015: 1-10.

[4] SHAABAN M, MOHANY A. Passive control of flow excited acoustic resonance in rectangular cavities using upstream mounted blocks[J]. Experiments in Fluids, 2015, 56(72): 1-12.

[5] ALHADDABI N, KONTIS K, ZARE-BEHTASH H. Control of low-speed cavity flow using steady jets[C]∥8th AIAA Flow Control Conference. Reston, VA: AIAA, 2016: 1-13.

[6] 楊黨國, 范召林, 李建強, 等. 后壁倒角對空腔噪聲的抑制效果[J]. 實驗流體力學, 2010, 24(5): 22-25.

YANG D G, FAN Z L, LI J Q, et al. Suppression effect of rear-face angle of cavity on aerodynamic noise[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(5): 22-25 (in Chinses).

[7] 寧方立, 史紅兵, 丘廉芳, 等. 前緣高頻振動對亞聲速開式空腔內強噪聲影響的數值研究[J]. 航空學報, 2015, 36(12): 3843-3852.

NING F L, SHI H B, QIU L F, et al. Numerical research of high frequency vibration effect on subsonic open cavity macro-noise[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3843-3852 (in Chinese).

[8] STANEK M J, RAMAN G, ROSS J, et al. High frequency acoustic suppression-the role of mass flow, the notion of superposition, and the role of inviscid instability-a new model (Part II)[C]∥8th AIAA/CEAS Aeroacoustics Conference & Exhibit. Reston, VA: AIAA, 2002: 1-30.

[9] SCHMIT R F, MCGAHA C, TEKELL J, et al. Performance results for the optical turbulence reduction cavity[C]∥47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Reston, VA: AIAA, 2009: 1-13.

[10] SCHMIT R F, SEMMELMAYER F, HAVERKAMP M, et al. Analysis of cavity passive flow control using high speed shadowgraph image[C]∥47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Reston, VA: AIAA, 2009: 1-13.

[11] SCHMIT R F, SEMMELMAYER F, HAVERKAMP M, et al. Examining passive flow control devices with high speed shadowgraph images around a Mach 1.5 cavity flow field[C]∥6th AIAA Flow Control Conference. Reston, VA: AIAA, 2013: 1-19.

[12] THANGAMANI V, KNOWLES K, SADDINGTON A J. The effects of scaling on high subsonic cavity flow oscillations and control[C]∥18th AIAA/CEAS Aeroacoustics Conference. Reston, VA: AIAA, 2012: 1-16.

[13] THANGAMANI V, KNOWLES K, SADDINGTON A J. An investigation of passive control methods for a large scale cavity model in high subsonic flow[C]∥19th AIAA/CEAS Aeroacoustics Conference. Reston, VA: AIAA, 2013: 1-13.

[14] SADDINGTON A J, KNOWLES K, THANGAMANIET V, et al. Scale effects on the performance of sawtooth spoilers in transonic rectangular cavity flow[J]. Experiments in Fluids, 2016, 57(2): 1-12.

[15] PANICKAR P, RAMAN G. Understanding the mechanism of cavity resonance suppression using a cylindrical rod in cross-flow[C]∥46th AIAA Aerospace Sciences Meeting and Exhibit. Reston, VA: AIAA, 2008: 1-27.

[16] PANICKAR P, RAMAN G. Cavity resonance suppression using high frequency excitation the mystery of the cylinder in crossflow revisited[C]∥14th AIAA/CEAS Aeroacoustics Conference. Reston, VA: AIAA, 2008: 1-24.

[17] DUDLEY J G, UKEILEY L. Suppression of fluctuating surface pressures in a supersonic cavity flow[C]∥5th Flow Control Conference. Reston, VA: AIAA, 2010: 1-22.

[18] DUDLEY J G, UKEILEY L. Detached eddy simulation of a supersonic cavity flow with and without passive flow control[C]∥20th AIAA Computational Fluid Dynamics Conference. Reston, VA: AIAA, 2011: 1-18.

[19] DUDLEY J G, UKEILEY L. Passively controlled supersonic cavity flow using a spanwise cylinder[J]. Experiments in Fluids, 2014, 55(9): 1-22.

[20] 楊黨國, 吳繼飛, 羅新福. 零質量射流對開式空腔氣動噪聲抑制效果分析[J]. 航空學報, 2011, 32(6): 1107-1114.

YANG D G, WU J F, LUO X F. Investigation on suppression effect of zero-net-mass-flux jet on aerodynamic noise inside open cavities[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(6): 1107-1114 (in Chinses).

[21] 吳亞東, 歐陽華, 黃友. 基于被動控制的空腔脈動壓力實驗研究[J]. 工程熱物理學報, 2013, 34(9): 1640-1644.

WU Y D, OUYANG H, HUANG Y. Experimental investigation on the fluctuating pressure of cavity based on passive controls[J]. Journal of Engineering Thermophysics, 2013, 34(9): 1640-1644 (in Chinese).

[22] 吳繼飛, 徐來武, 范召林, 等. 開式空腔氣動聲學特性及其流動控制方法[J]. 航空學報, 2015, 36(7): 2015-2165.

WU J F, XU L W, FAN Z L, et al. Aeronautica characteristics and flow control method of open cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2015-2165 (in Chinese).