脈沖射流沖擊平直表面的對流換熱實驗
呂元偉,張靖周, 2, *,唐嬋,單勇
1.南京航空航天大學 能源與動力學院 江蘇省航空動力系統重點實驗室,南京 210016 2.先進航空發動機協同創新中心,北京 100083
射流沖擊是強化局部換熱的一種有效技術途徑,在動力裝置熱端部件強化冷卻、飛行器表面熱氣防冰、電子器件高效散熱等許多技術領域得到廣泛應用[1-3]。
長期以來,射流沖擊強化傳熱一直是國內外研究人員關注的研究課題,尤其是20世紀80年代以來,為適應高新科學技術發展所帶來的日益增長的高效傳熱需求,研究人員更加注重射流沖擊強化措施的創新研究[4],發展了一系列被動(如異型噴嘴、處理靶面和渦激勵等[5-9])或主動(如基于機械間斷、聲學或電磁效應等方式形成的脈沖射流和合成射流[10-14])的強化傳熱技術措施。與連續射流沖擊相比,非穩定脈沖射流在沖擊換熱的機制上更為復雜,由于脈沖射流具有的脈動特征,一方面增強了射流湍流強度,周期性地破壞熱邊界層;另一方面,導致射流與周圍流體摻混加劇,使射流核心區速度降低,因此脈沖射流相對于穩定連續射流沖擊能否形成換熱增強效果,與射流固有的脈沖特征(波形、頻率、幅值)以及射流時均雷諾數、射流沖擊間距等密切相關。Sheriff和Zumbrunnen[15]提出了用無量綱的斯特勞哈爾數(Sr=fD/um,f為脈沖頻率,D為噴管直徑,um為射流平均速度)來評判脈沖射流與連續射流對沖擊靶板換熱的影響,其研究表明在較小的斯特勞哈爾數范圍內(0.012≤Sr≤0.144),脈沖射流相對連續射流的對流換熱系數相對降低17%,而在較高的斯特勞哈爾數下(Sr=0.51)則相對增強33%。然而針對不同的射流雷諾數和脈沖頻率范圍,臨界斯特勞哈爾數卻并不相同[16-18],尤其是對于沖擊間距的影響,甚至出現截然相反的結果,譬如,Hofmann等[19]利用高速電磁閥激勵的脈沖射流沖擊換熱實驗表明(時均射流雷諾數Re范圍為14 000~78 000,2 Hz≤f≤400 Hz),在小沖擊間距比(H/D=2,H為射流管到耙板的距離)下,脈沖射流駐點對流換熱系數增強最為明顯,而在大間距比和很小的斯特勞哈爾數下則呈現換熱下降的趨勢。Behera等[20]研究了25 Hz≤f≤400 Hz(對應于0.008≤Sr≤0.13)、5≤H/D≤9時的脈沖射流沖擊換熱,發現即便在較小的斯特勞哈爾數下脈沖射流依然具有高于連續射流的對流換熱系數。Persoons等[21]通過系統的實驗,研究了6 000≤Re≤14 000、9 Hz≤f≤55 Hz的脈沖射流沖擊換熱,指出當Sr(H/D)>0.1時脈沖射流相對于連續射流具有更強的對流換熱能力。
脈沖射流沖擊換熱的影響因素眾多,對此,本文通過實驗研究脈沖射流沖擊平直表面的對流換熱特性,并進一步闡明其與連續射流換熱性能差異的主導因素。
1 實驗描述
1.1 實驗系統
脈沖射流沖擊換熱實驗系統如圖1所示。沖擊射流由小型空氣壓縮機提供,經過調節閥和流量控制器進入脈沖射流激勵裝置,脈沖射流由電磁閥激勵形成,通過信號發生器對電磁閥兩端的電壓占空比進行控制,進而得到按照特定規律周期性變化的脈沖射流。本文實驗中,射流管直徑D=10 mm,長徑比L/D=12(L為射流管長度)。
圖2為時均射流雷諾數Re=10 000工況下,運用熱線風速儀測試獲得的噴管出口中心位置(H/D=0)上,脈沖射流占空比A=50%、脈沖頻率f=10 Hz時的脈沖射流速度隨時間的變化,圖中T為脈沖射流周期。對于連續射流,噴管出口的速度也存在非常微弱的變化,但總體可以視為是連續穩定的;對于脈沖射流,在電磁閥開通的值班周期內射流的速度為連續性射流速度的2倍,處于電磁閥閉合的周期間隔內孔口出口中心位置的速度接近1 m/s,這是由于射流管內的氣流慣性所致。總體而言,本文的實驗裝置能夠產生滿足要求的脈沖射流。
在射流沖擊換熱實驗中,將加熱膜固定在圓形銅棒上,銅棒兩端施加電壓,熱膜加熱的熱流由直流穩壓電源提供。為了使得熱膜表面平整,在熱膜兩端施加一定的張緊力,加熱表面溫度由紅外熱像儀測量。本文研究中,脈沖射流的頻率和占空比分別恒定為10 Hz和50%,改變射流的雷諾數和沖擊間距,主要實驗參數列于表1。
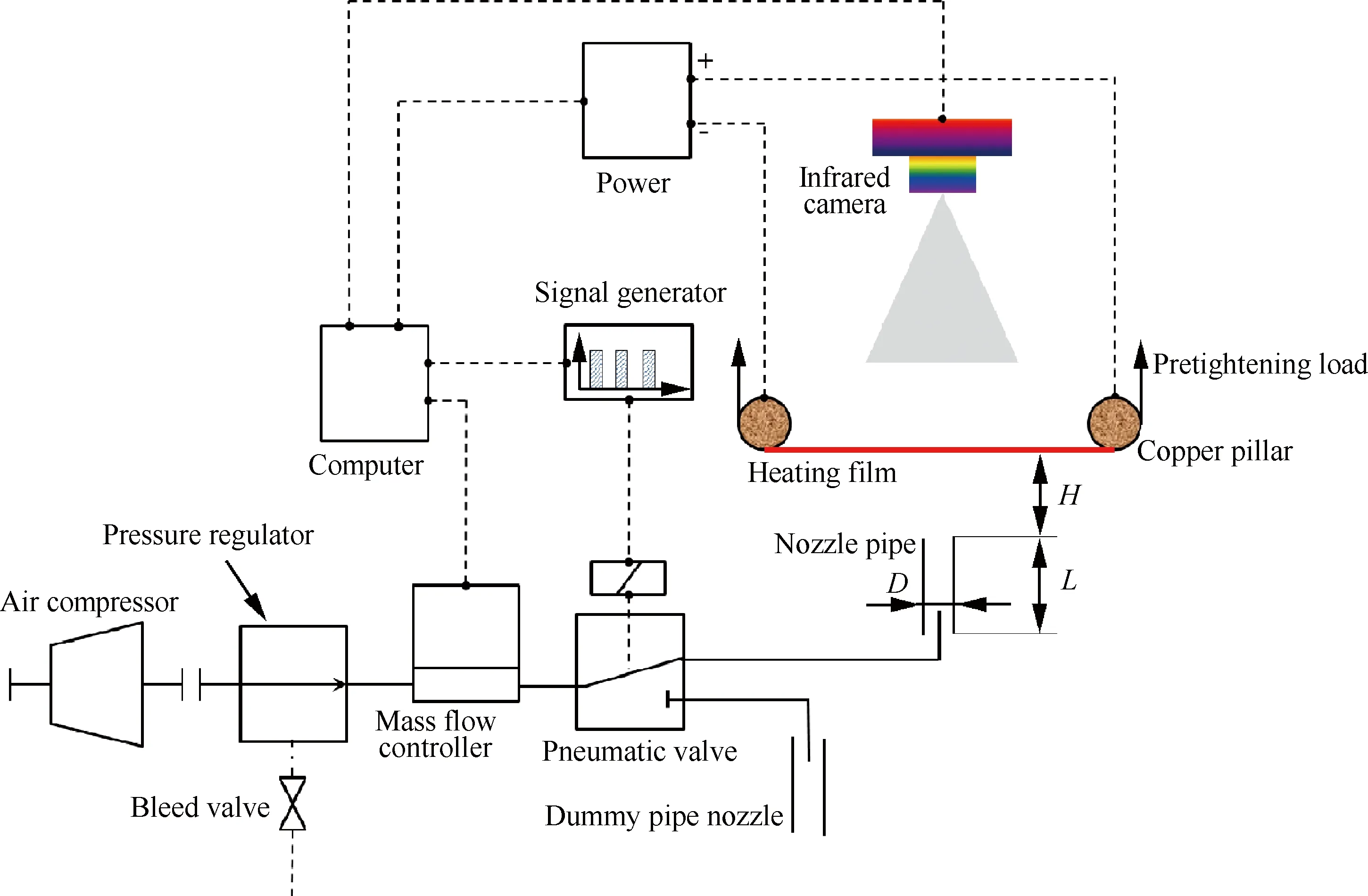
圖1 脈沖射流沖擊換熱實驗系統示意圖Fig.1 Schematic of experimental system of pulsed jet impingement heat transfer
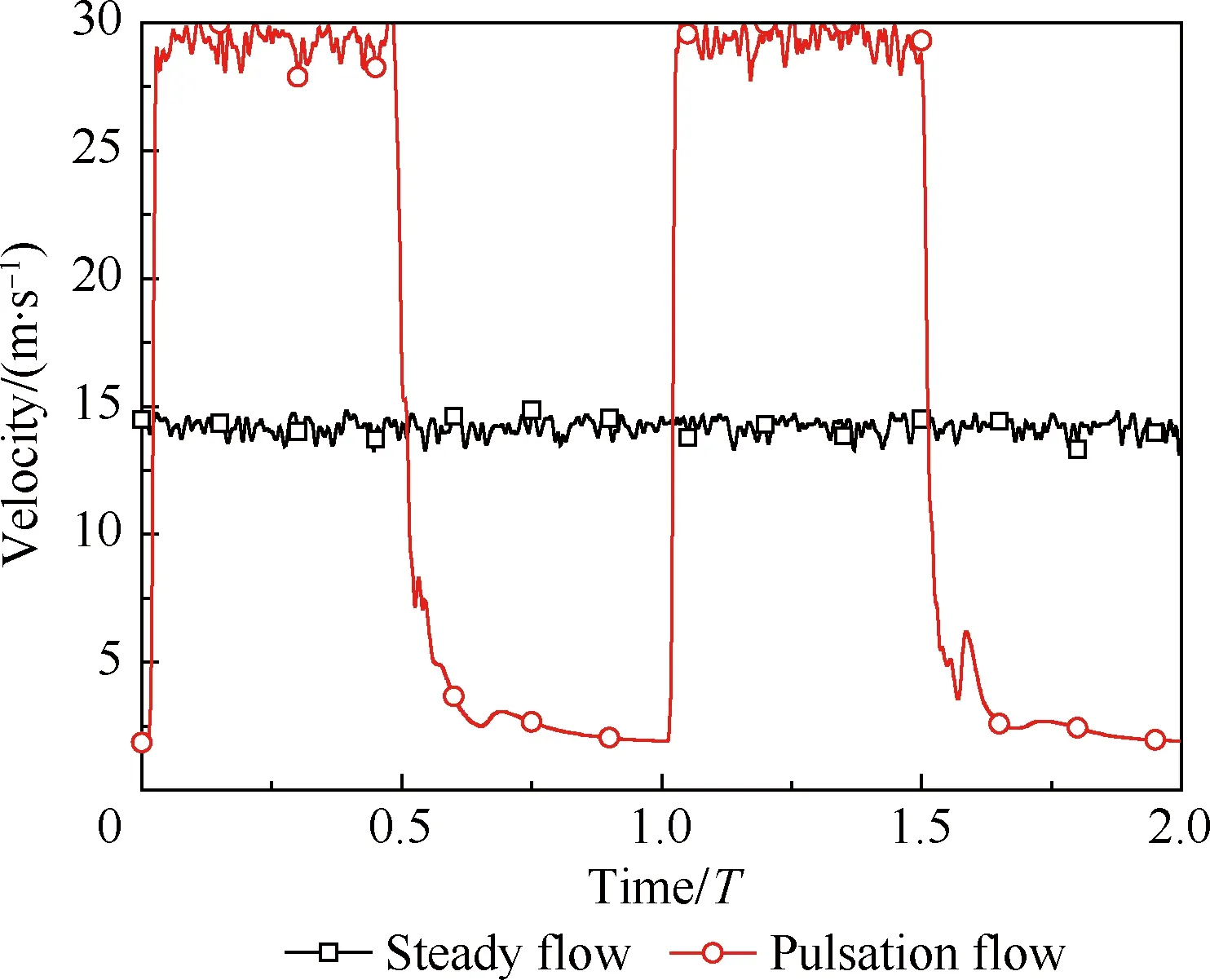
圖2 噴管出口脈沖射流速度隨時間的變化Fig.2 Variation of velocity of pulsed jet at nozzle outlet with time
表1 主要實驗參數Table 1 Main experimental parameters
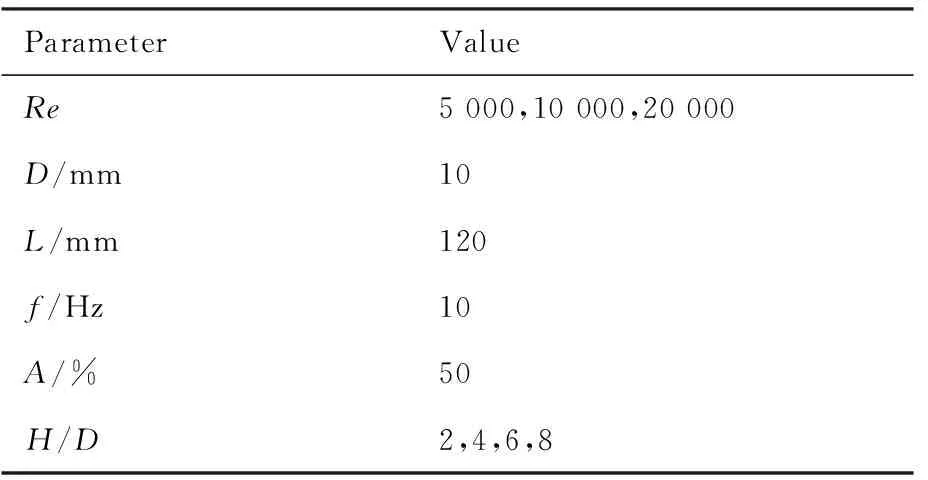
ParameterValueRe5000,10000,20000D/mm10L/mm120f/Hz10A/%50H/D2,4,6,8
1.2 實驗測試和數據處理
加熱表面溫度采用工作波段為8~14 μm的紅外熱像儀測試,為保障紅外測溫精度,將加熱表面預先均勻地噴涂黑漆[22-23],標定實驗結果表明測試表面的發射率約為0.96。
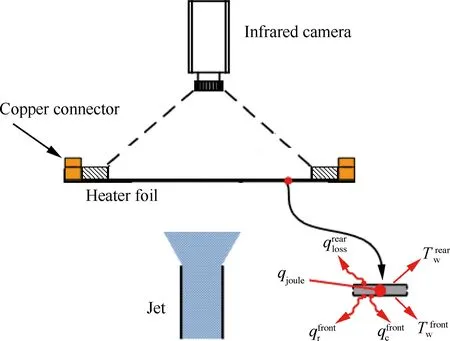
圖3 加熱表面熱流平衡模型示意圖Fig.3 Schematic of heat balance model on heater foil
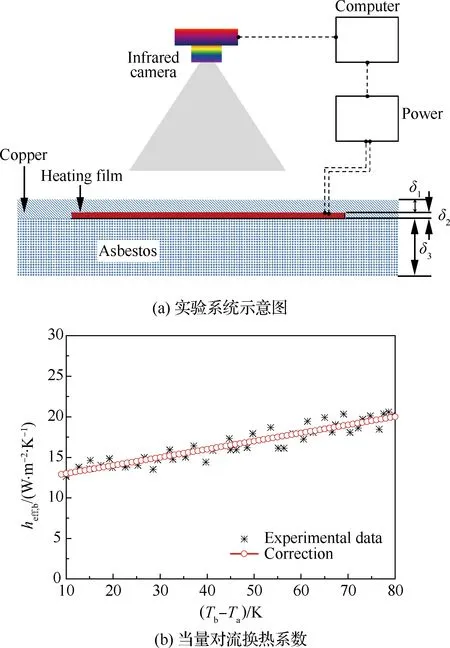
圖4 加熱表面散熱損失預測實驗Fig.4 Pre-test for estimating heat loss on heater foil
加熱表面背側的熱流損失通過預先進行的標定實驗加以預測,如圖4(a)所示,即將加熱膜放置于厚度δ3=30 mm的絕熱石棉板上,用厚度δ1=0.5 mm的銅板壓緊在加熱膜(厚度為δ2)上,通過調節加熱膜的輸入電流,得到不同加熱熱流密度下的表面溫度,由能量方程可知,顯然上述測試得到的散熱損失來源于表面的自然對流以及輻射換熱。即
(1)
式中:heff,b為計及自然對流和輻射散熱的當量對流換熱系數;Tb為熱膜表面溫度;Ta為環境溫度。
圖4(b)為實驗測得的表面當量對流換熱系數隨表面和環境溫度差的變化,在本文研究的溫度差范圍內基本呈現線形變化的趨勢,擬合得到熱膜上表面的當量對流換熱系數heff,b(單位為W/(m2·K))為
heff,b=0.11(Tb-Ta)+12
(2)
加熱膜射流沖擊側與環境之間的輻射換熱量可以近似處理為
(3)
式中:Tw和εw分別為加熱膜表面溫度和發射率;σ為Stefan-Boltzmann常數。
由此,射流沖擊的局部對流換熱系數為
(4)
式中:Tj為沖擊射流溫度,在低的射流速度下,沖擊射流的靜溫與其總溫可視為相同,由噴管出口處的溫度探針測得。
理論上,脈沖射流作用下壁面溫度呈現出周期性的變化規律。但是當經歷了一定的周期后,壁面上的溫度趨于準穩定狀態,即在一個周期內壁面溫度變化極其微弱。定義射流沖擊局部努塞爾數Nu為
(5)
式中:k為射流的導熱系數。
本文引入了兩種平均方式來確定射流沖擊平均努塞爾數,即
1) 周向平均,取射流駐點徑向位置處的周向值進行平均,記為NuL-Average。
2) 局部區域平均,沿射流駐點徑向位置包絡的區域進行平均,記為NuR-Average。
實驗測試中,所有實驗數據的重復度為2.5%。本實驗中質量流量控制器的精度為3.3%;考慮輻射和自然對流帶來熱損失時,平板當量熱流密度qtarget計算比較復雜,本實驗精度設定為5%;射流溫度Tj和環境溫度Ta由K型熱電偶測得,精度為±0.5 ℃;平板表面的溫度Tw由紅外熱像儀獲得,精度為±2%|t|(|t|為熱像儀獲得的測量溫度與環境溫度的差值)。同時,噴嘴出口直徑D的測量不確定度為1%。考慮到溫度的變化引起流體熱物性的變化,由誤差傳遞函數[24],可得靶板表面的努塞爾數誤差為5.5%。射流雷諾數的誤差為7.5%。
1.3 實驗方法驗證
Violato等[25]得到了Re=10 000工況,不同沖擊間距比H/D下表面周向平均努塞爾數NuL-Average沿R/D的分布規律(誤差小于3.5%),本文參考Violato等的穩定射流沖擊實驗工況進行了實驗方法驗證,實驗中R為以滯止中心位置為原點時拾取區域的半徑。圖5為本文實驗獲得的平板表面努塞爾數和Violato等的實驗數據比較。可以看出,在H/D=2、4時,本文得到的射流駐點附近的努塞爾數略高于Violato等的實驗數據,而在H/D=8時,本文的實驗結果略低于Violato等的實驗數據。但是在R/D>1.5后,本文的實驗結果與Violato等的實驗數據吻合良好,兩者的最大誤差在7%以內。
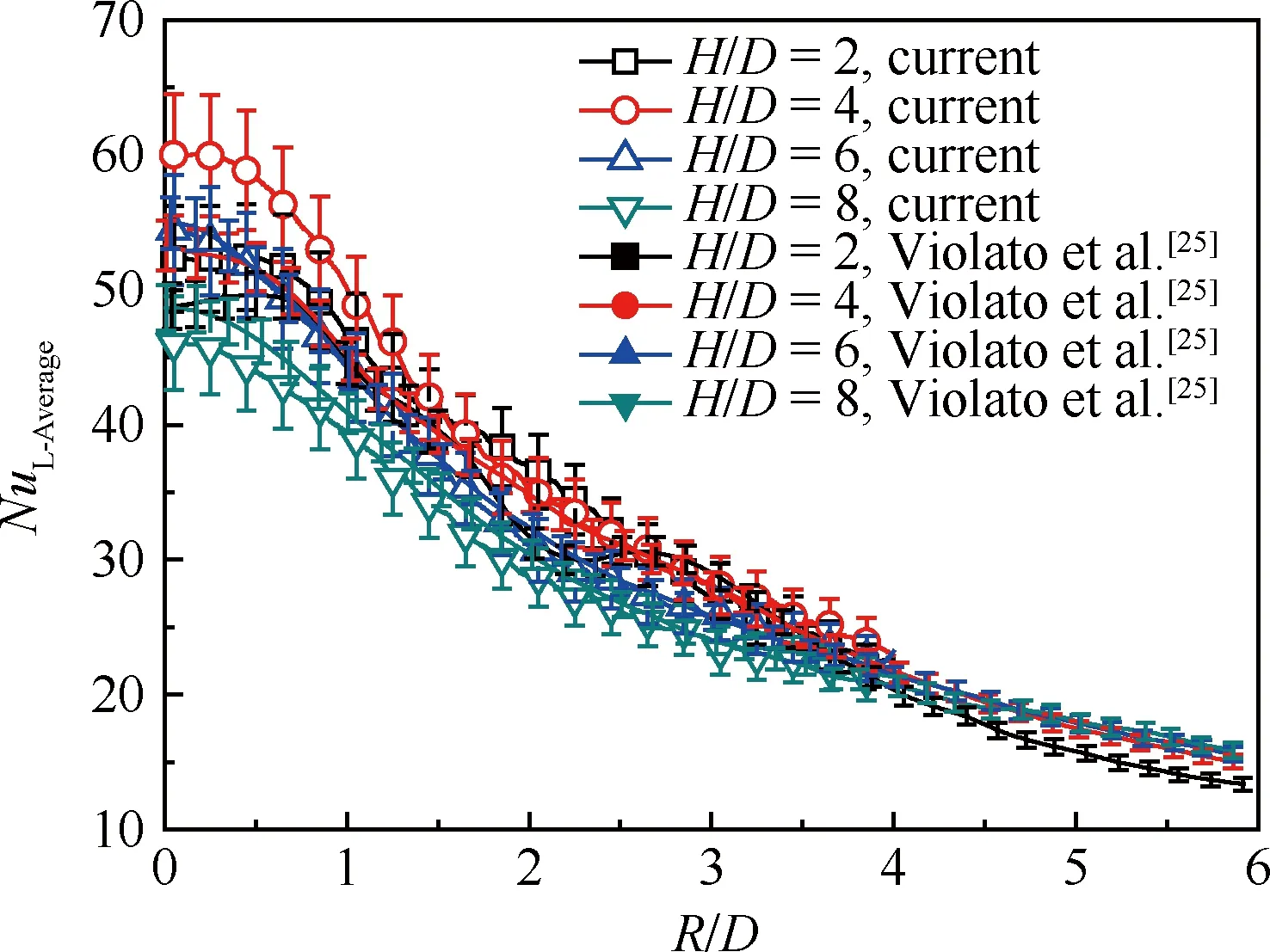
圖5 本文實驗結果與Violato等[25]的比較Fig.5 Comparison between current experimental results and results obtained by Violato et al.[25]
2 實驗結果與分析
2.1 努塞爾數徑向分布
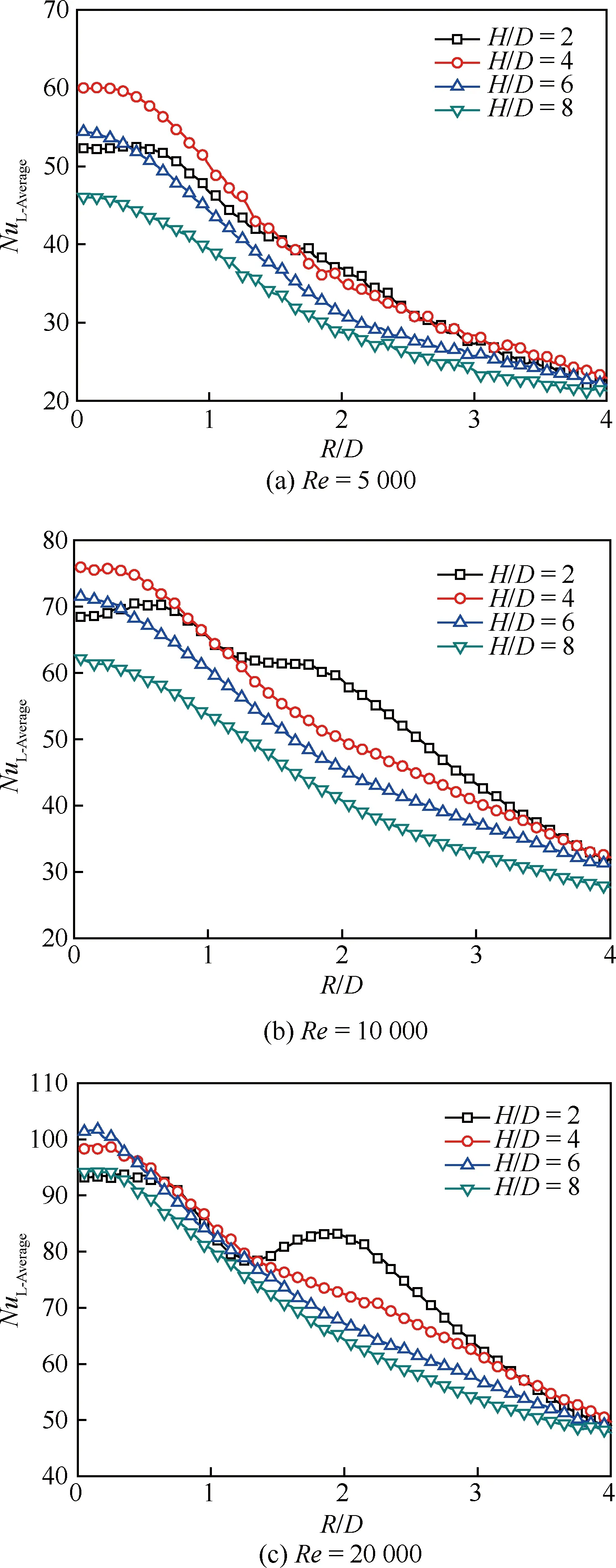
圖6 連續射流沖擊時平板表面的周向平均 努塞爾數沿徑向的分布 Fig.6 Distribution of line-averaged Nusselt number on plate surface along radial direction for continuous jet impingement
圖6為連續性射流沖擊時平板表面的周向平均努塞爾數NuL-Average沿徑向的分布規律。隨著射流雷諾數的增加,射流沖擊周向平均努塞爾數呈現持續增大的趨勢;在Re=5 000和Re=10 000工況下,射流駐點區的周向平均努塞爾數在射流沖擊間距比H/D=4最高,在Re=20 000工況下,射流駐點區的周向平均努塞爾數換熱最大值則出現在H/D=6的射流沖擊間距比。同時射流沖擊周向平均努塞爾數沿徑向基本呈現急劇降低的變化趨勢,這是駐點區射流法向沖擊壁面形成壁面射流的作用特征,但在小的射流沖擊間距比H/D=2時,NuL-Average在R/D=2徑向位置處呈現第2個峰值,這是因為在小的射流沖擊間距下,射流趨赴壁面的速度高,從而對近駐點區的壁面射流形成強烈的擾動,使得局部對流換熱能力提高。
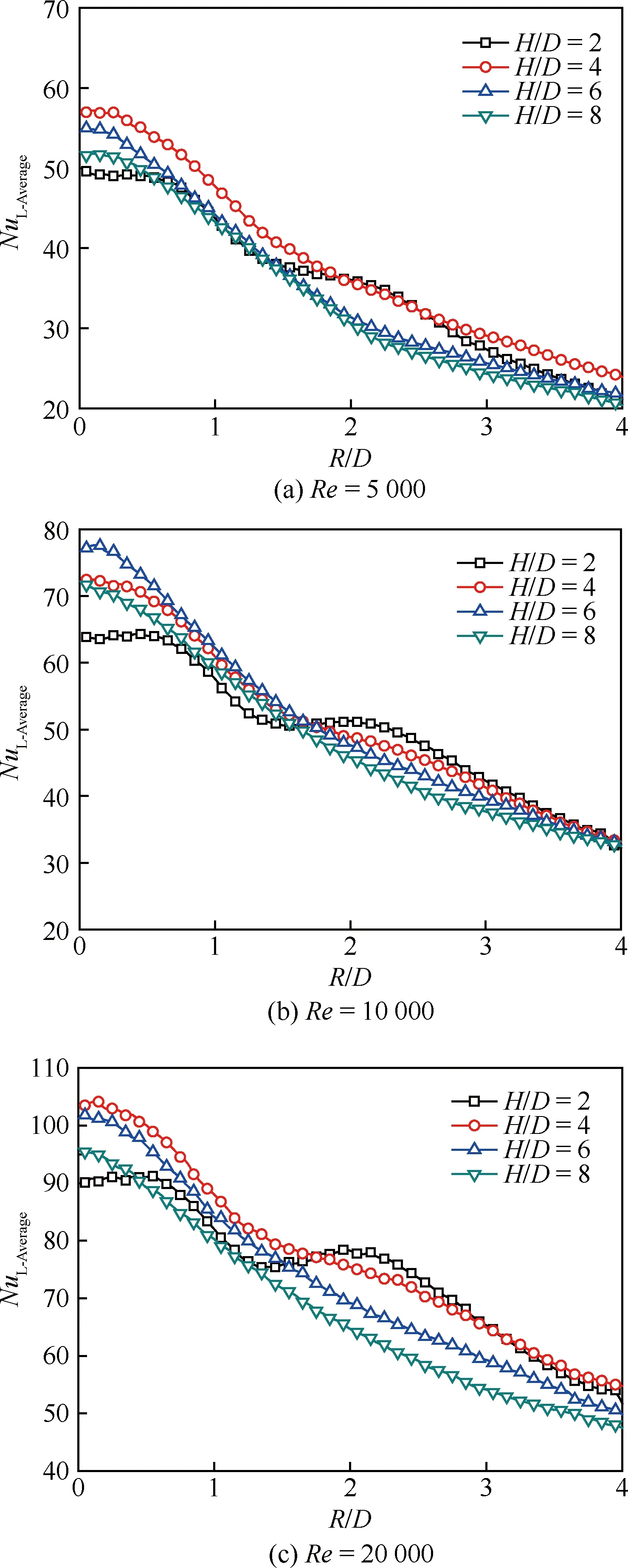
圖7 f=10 Hz的脈沖射流沖擊時平板表面的周向 平均努塞爾數沿徑向的分布 Fig.7 Distribution of line-averaged Nusselt number on plate surface along radial direction for pulsed jet impingement with f=10 Hz
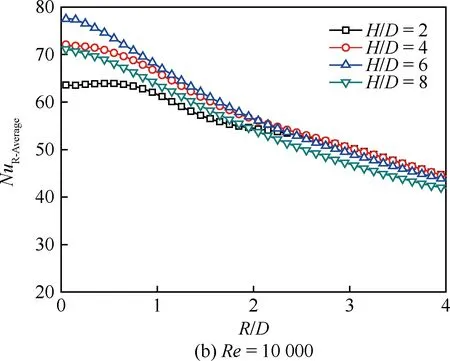
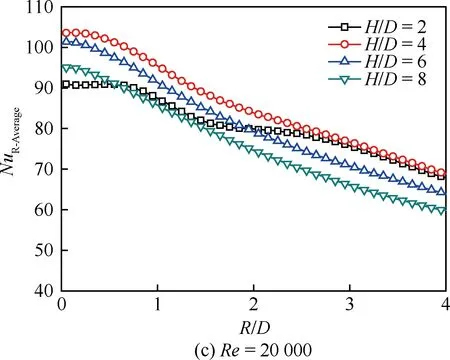
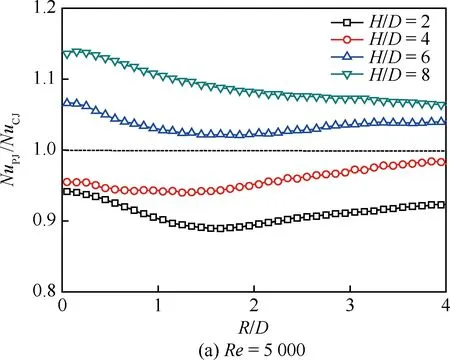
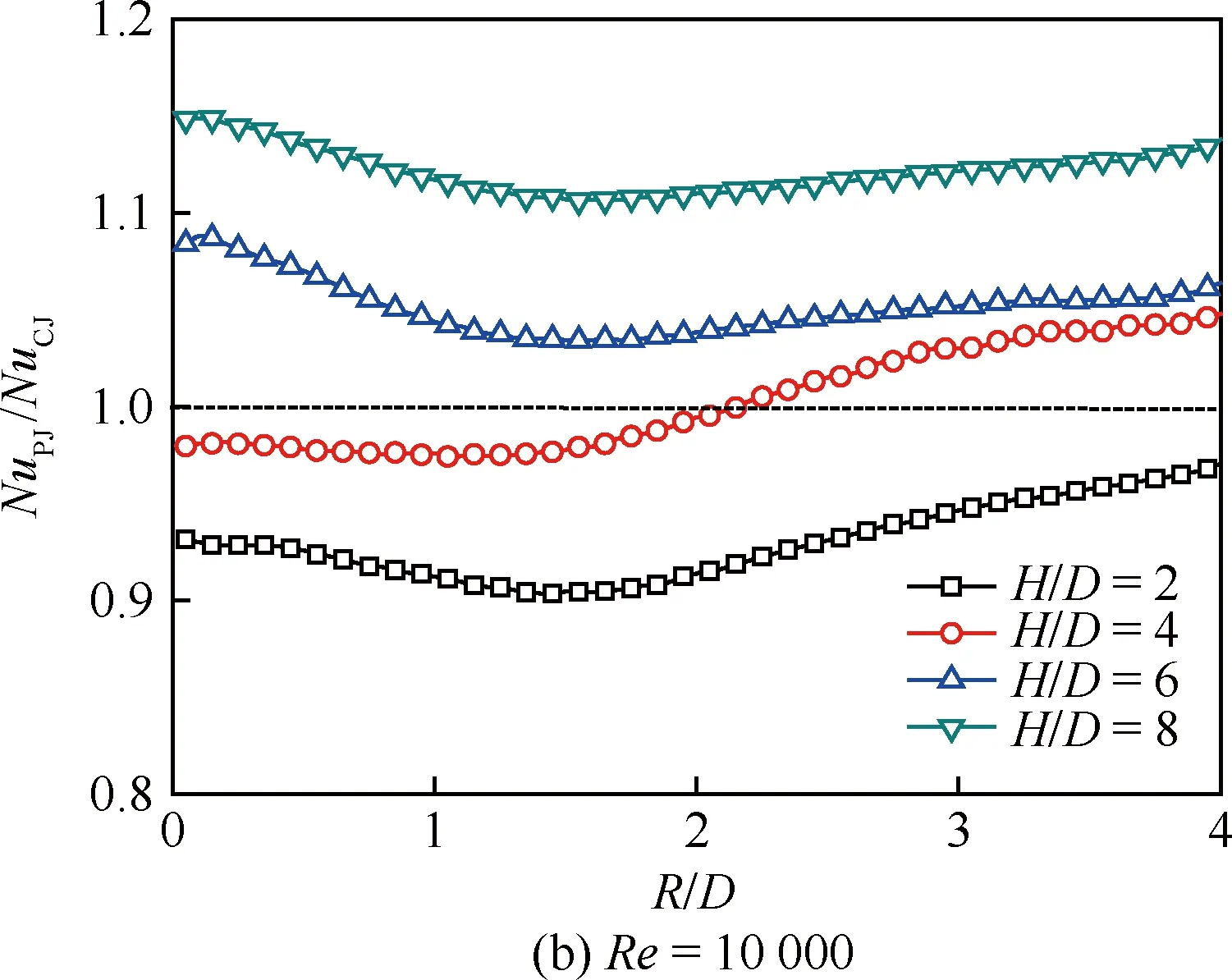
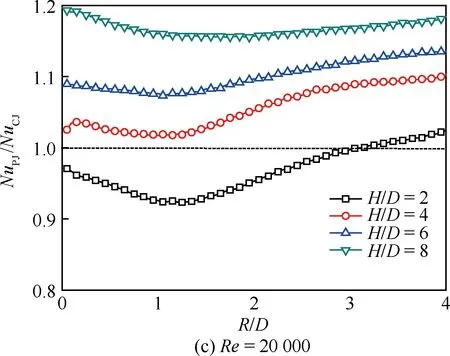
圖7為f=10 Hz的脈沖射流沖擊時平板表面的周向平均努塞爾數NuL-Average沿徑向的分布規律。與連續射流沖擊相比,可以看出脈沖射流沖擊的周向平均努塞爾數依然具有隨射流雷諾數增加而提高、沿徑向急劇降低等基本特征,但是注意到脈沖射流沖擊將引起若干差異。在大射流沖擊間距比下(H/D=8),脈沖射流在射流駐點區對流換熱能力較連續射流有所提高,在雷諾數較小的工況下體現尤為明顯;而在小射流沖擊間距比下(H/D=2),脈沖射流在射流駐點區對流換熱能力則弱于連續射流。對于偏離射流駐點區的壁面射流區,脈沖射流也呈現較為復雜的影響規律,譬如,在Re=5 000時,H/D=4下的脈沖射流雖然在駐點區的對流換熱弱于連續射流,但其在壁面射流區2 圖8 f=10 Hz的脈沖射流沖擊時平板表面的局部 區域平均努塞爾數沿徑向的分布 Fig.8 Distribution of local region-averaged Nusselt number on plate surface along radial direction for pulsed jet impingement with f=10 Hz 圖8為f=10 Hz的脈沖射流沖擊時平板表面的局部區域平均努塞爾數NuR-Average沿徑向的分布規律。若以一倍射流管直徑作為圓形區域半徑進行平均,脈沖射流的局部區域平均努塞爾數均在H/D=4和H/D=6時較優,H/D=2時最低;然而,若以2~4倍射流管直徑作為圓形區域半徑進行平均,則在H/D=4和H/D=2時相對較優,H/D=8時最低。在本文所研究的特定脈沖激勵方式下,H/D=4是相對較優的沖擊間距比。 鑒于射流沖擊局部強化傳熱的特點,以局部區域平均作為對比基準評價脈沖射流相對連續射流的沖擊換熱效果,即采用脈沖射流局部區域平均的努塞爾數NuPJ與連續性射流局部區域平均的努塞爾數NuCJ之比進行表示。圖9反映了典型射流雷諾數下沖擊間距的影響。 圖9 基于局部區域平均方式的H/D對 NuPJ/NuCJ的影響Fig.9 Effect of H/D on NuPJ/NuCJbased on local region-averaged mode 由圖9可以看出,在Re=5 000時,射流沖擊間距比H/D=6和H/D=8下的脈沖射流較連續射流可以獲得更好的強化換熱效果;隨著射流雷諾數的增加,H/D=4下的脈沖射流較連續射流也逐漸顯示出傳熱強化的效果,在Re=20 000下脈沖射流的區域平均努塞爾數可以相對提高15%~20%;但在H/D=2時,基本都是以連續射流沖擊為優,即便在Re=20 000下,僅當以3倍射流管直徑作為區域半徑進行平均時,脈沖射流才具有略高于連續射流沖擊換熱的作用效果。 本文通過實驗,研究了脈沖頻率為10 Hz、占空比為50%的脈沖射流沖擊平板的對流換熱,在射流雷諾數為5 000~20 000、沖擊間距比為2~8范圍內與相同工況下的連續射流進行了比較分析。主要結論如下: 1) 脈沖射流沖擊的努塞爾數依然具有隨射流雷諾數增加而提高、沿徑向急劇降低等基本特征,但是與連續射流相比,脈沖射流沖擊會引起射流駐點和壁面射流區的對流換熱差異,其影響與射流雷諾數和射流沖擊間距密切相關。 2) 以局部區域平均作為對比基準評價脈沖射流相對連續射流的沖擊換熱效果,在大的射流沖擊間距比下(H/D=6、8),脈沖射流體現出傳熱增強的效果,而在小的射流沖擊間距比下(H/D=2),連續射流更具優勢。 3)Re=20 000工況下,僅當以3倍以上射流管直徑作為區域半徑進行平均時,脈沖射流才具有略高于連續射流沖擊換熱的作用效果。 [1] VISKANTA R. Heat transfer to impinging isothermal gas and flame jets[J]. Experimental Thermal and Fluid Science, 1993, 6(2): 111-134. [2] BUNKER R S. Gas turbine heat transfer: Ten remaining hot gas path challenges[J]. ASME Journal of Turbomachinery, 2007, 129(2): 193-210. [3] FREGEAU M, GABR M, PARASCHIVOIU I, et al. Simulation of heat transfer from hot-air jets impinging a three-dimensional concave surface[J]. Journal of Aircraft, 2009, 46(2): 721-725. [4] CARLOMAGNO G M, IANIRO A. Thermo-fluid-dynamics of submerged jets impinging at short nozzle-to-plate distance: A review[J]. Experimental Thermal and Fluid Science, 2014, 58: 15-35. [5] COLUCCI D W, VISKANTA R. Effect of nozzle geometry on local convective heat transfer to a confined impinging air jet[J]. Experimental Thermal and Fluid Science, 1996, 13(1): 71-80. [6] NAKOD P M, PRABHU S V, VEDULA R P. Heat transfer augmentation between impinging circular air jet and flat plate using finned surfaces and vortex generators[J]. Experimental Thermal and Fluid Science, 2008, 32(5): 1168-1187. [7] YANG H Q, KIM T, LU T J, et al. Flow structure, wall pressure and heat transfer characteristics of impinging annular jet with/without steady swirling[J]. International Journal of Heat and Mass Transfer, 2010, 53(19): 4092-4100. [8] VIOLATO D, SCARANO F. Three-dimensional evolution of flow structures in transitional circular and chevron jets[J]. Physics of Fluids, 2011, 23(12): 124104. [9] YU Y Z, ZHANG J Z, XU H S. Convective heat transfer by a row of confined air jets from round holes equipped with triangular tabs[J]. International Journal of Heat and Mass Transfer, 2014, 72: 222-233. [10] ZUMBRUNNEN D A, AZIZ M. Convective heat transfer enhancement due to intermittency in an impinging jet[J]. ASME Journal of Heat Transfer, 1993, 115(1): 91-98. [11] 周靜偉, 楊興賢, 耿麗萍, 等. 非穩態沖擊射流強化傳熱試驗研究[J]. 機械工程學報, 2010, 46(6): 144-148. ZHOU J W, YANG X X, GENG L P, et al. Experimental investigation on heat transfer augmentation with unsteady impinging jet[J]. Journal of Mechanical Engineering, 2010, 46(6): 144-148 (in Chinese). [12] ZHOU J W, WANG Y G, MIDDELBERG G, et al. Unsteady jet impingement heat transfer on smooth and non-smooth surfaces[J]. International Communications in Heat and Mass Transfer, 2009, 36(2): 103-110. [13] VALIORGUE P, PERSOONS T, MCGUINN A, et al. Heat transfer mechanisms in an impinging synthetic jet for a small jet-to-surface spacing[J]. Experimental Thermal and Fluid Science, 2009, 33(4): 597-603. [14] ZHANG J Z, GAO S, TAN X M. Convective heat transfer on a flat plate subjected to normally synthetic jet and horizontally forced flow[J]. International Journal of Heat and Mass Transfer, 2013, 57(1): 321-330. [15] SHERIFF H, ZUMBRUNNEN D. Effect of flow pulsations on the cooling effectiveness of an impinging jet[J]. ASME Journal of Heat Transfer, 1994, 116(4): 886-895. [16] HERWIG H, MIDDELBERG G. The physics of unsteady jet impingement and its heat transfer performance[J]. Acta Mechanics, 2008, 201(1): 171-184. [17] MEDINA H, BENARD E, EARLY J M. Reynolds number effects on fully developed pulsed jets impinging on flat surfaces[J]. AIAA Journal, 2013, 51(10): 2305-2318. [18] ALIMOHAMMADI S, MURRAY D B, PERSOONS T. On the numerical-experimental analysis and scaling of convective heat transfer to pulsating impinging jets[J]. International Journal of Thermal Sciences, 2015, 98: 296-311. [19] HOFMANN H T, MOVILEANU D L, KIND M, et al. Influence of a pulsation on heat transfer and flow structure in submerged impinging jets[J]. International Journal of Heat and Mass Transfer, 2007, 50(17-18): 3638-3648. [20] BEHERA R C, DUTTA P, SRINIVASAN K. Numerical study of interrupted impinging jets for cooling of electronics[J]. IEEE Transactions on Components and Packaging Technologies, 2007, 30(2): 275-284. [21] PERSOONS T, BALGAZIN K, BROWN K, et al. Scaling of convective heat transfer enhancement due to flow pulsation in an axisymmetric impinging jet[J]. ASME Journal of Heat Transfer, 2013, 135(11): 111012. [22] TAN X M, ZHANG J Z. Flow and heat transfer characteristics under synthetic jets impingement driven by piezoelectric actuator [J]. Experimental Thermal and Fluid Science, 2013, 48: 134-146. [23] 李鑫郡, 張靖周, 譚曉茗. 單個壓電風扇傳熱特性研究[J]. 航空學報, 2017, 38(7): 120982. LI X J, ZHANG J Z, TAN X M. Characteristics of heat transfer with a single piezoelectric fan[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 120982 (in chinese). [24] MOFFAT R J. Describing the uncertainties in experimental results[J]. Experimental Thermal and Fluid Science, 1998, 1(1): 3-17. [25] VIOLATO D, IANIRO A, CARDONE G, et al. Three-dimensional vortex dynamics and convective heat transfer in circular and chevron impinging jets[J]. International Journal of Heat and Fluid Flow, 2012, 37: 22-36.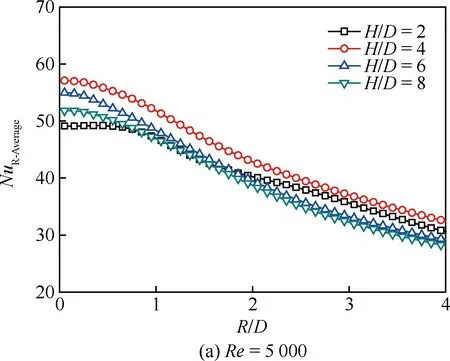
2.2 脈沖射流與連續射流沖擊換熱的比較
3 結 論

