超臨界壓力下碳氫燃料裂解與流動傳熱模擬的快速算法

黃世璋，阮波，高效偉，劉華雩

大連理工大學 航空航天學院，大連 116024

超燃沖壓發動機是高超聲速飛行器的理想動力裝置，具有良好的軍事和民用價值，受到了世界各國的重視。由于飛行速度快，飛行器受到氣動加熱和燃燒釋熱的雙重作用，發動機熱防護性能亟待提升。采用吸熱型碳氫燃料作為冷卻劑的主動再生冷卻技術是目前最有效的冷卻方式之一，在超燃沖壓發動機熱防護中發揮著重要作用[1-2]。主動再生冷卻技術是利用吸熱型碳氫燃料的對流傳熱來實現對發動機的冷卻，而高分子碳氫燃料的熱裂解化學反應吸熱可明顯提升燃料的冷卻能力[3-5]。此外，裂解反應產生的小分子碳氫化合物燃燒反應速度快，也是提高燃燒性能的關鍵[6-8]。因此準確預測超燃沖壓發動機冷卻通道中燃料的裂解特性對超燃沖壓發動機的設計非常關鍵。

研究碳氫燃料裂解特性需要建立可靠的化學反應機理，國內外對此進行了大量研究。Zhong等[9-10]對壓力為3.5～4.5 MPa、溫度為700～1 100 K條件下的RP-3航空煤油熱裂解反應進行了實驗研究，得到了煤油熱解產物的分布特性，在此基礎上建立了一步總包反應機理。Jiang等[11]對RP-3航空煤油在5 MPa下的傳熱和裂解現象開展了詳細的實驗研究，提出了適用于航空煤油的詳細化學反應機理。Stewart等[12]研究了超臨界十氫化萘、四氫化萘和正癸烷的熱解反應，獲得了主要的裂解產物分布并建立了一步總包反應機理。Ward等[13-14]對正癸烷裂解與傳熱過程進行了實驗研究，并采用成比例產物分布(Proportional Product Distribution, PPD)化學模型建立了適用于壓力在3.45～11.38 MPa范圍內正癸烷輕度裂解的一步總包反應機理，即平均PPD機理。Zhu等[15]也對超臨界壓力正癸烷的輕度裂解和傳熱現象開展了實驗研究，基于實驗結果提出了一步總包反應機理。

在建立反應機理的基礎上，數值模擬已成為研究碳氫燃料裂解與傳熱的重要手段。從基礎研究方面來看，正癸烷與真實煤油熱物性非常相似[16]，因此許多學者采用正癸烷作為航空煤油的替代燃料來研究吸熱型碳氫燃料的超臨界傳熱與裂解吸熱反應的耦合作用機制。阮波和孟華[17]建立了通用的碳氫燃料裂解混合物物性計算方法，進一步基于平均PPD反應機理[14]建立了考慮正癸烷裂解吸熱及超臨界傳熱現象的數值計算模型，通過與已有的實驗和數值計算結果比較，驗證了數值模型的可靠性。Bao等[4]模擬了三維冷卻通道內正癸烷的裂解傳熱現象，分析了溫度、速度和正癸烷質量分數在冷卻通道內的分布。與不考慮裂解情況相比，裂解反應使得流場溫度和燃料熱沉在截面上的分布變得更均勻。Zhang等[18]研究了冷卻通道橫截面高寬比對正癸烷裂解和傳熱過程的影響。增大高寬比后通道內出現明顯的熱分層和裂解度不均勻現象，不利于燃料化學熱沉的利用。Feng等[19]對圓管內超臨界壓力正癸烷的裂解與流動傳熱進行了數值模擬，分析了管內傳質傳熱與裂解反應的相互影響機制。

由于裂解產物的復雜性，即便采用簡化反應機理，其巨大的計算開銷依然是進行大規模數值研究的主要困難。目前提高計算效率的主要途徑有物性快速算法和反應機理簡化方法。劉志琦[20]基于SUPERTRAPP軟件生成的三維物性數據庫，建立了高效查表方法，顯著提升了正癸烷裂解傳熱計算效率。程澤源和朱劍琴[21]建立了低裂解度正癸烷物性快速算法，并分析了算法的效率和精度。Ruan等[22]對平均PPD機理[14]進行了簡化，提出了一個12組分的模型，該模型在保證精度的前提下具有更高的計算效率。物性快速算法會提升計算效率，然而仍需求解數目龐大的組分輸運方程；反應機理簡化會減少組分輸運方程數量，但受精度限制簡化程度始終有限。

本文在前期研究的基礎上[17]，通過數值分析和理論推導對算法進行改進和優化，建立了一套快速算法。與目前已有的求解全組分輸運方程的算法相比，該快速算法只需求解1個組分輸運方程，但是依然考慮了各組分的輸運過程。通過與全組分輸運方程算法以及現有的實驗和數值結果進行對比，全面考察了算法的計算效率和精度。最后采用該算法對三維矩形截面冷卻通道內的正癸烷裂解和傳熱過程進行數值模擬研究。該方法的建立對于提高碳氫燃料裂解與傳熱數值模擬的計算效率具有重要意義。

1 數值模型

1.1 守恒方程

本文研究碳氫燃料裂解吸熱化學反應與湍流傳熱的耦合過程，在數值模擬過程中，需要求解連續性方程、動量方程、組分輸運方程、能量方程以及湍流控制方程。

連續性方程：

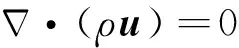
(1)

式中：ρ為流體密度；u為速度。

動量方程：

(2)

式中：p為壓力；τeff為黏性應力張量。

組分輸運方程：

(3)

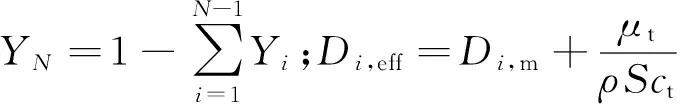
(4)

能量方程：

(5)

式中：etol為總內能；T為溫度；λ為導熱系數；cp為定壓比熱；Prt=0.85為湍流普朗特數。

標準k-ε湍流控制方程：

(6)

(7)

式中：k為湍動能；ε為耗散率；μ為黏性系數；Gk為湍動能生成項；σk、σε為k-ε方程的普朗特數；C1=1.44和C2=1.92為常數。為了準確捕捉近壁面參數變化，采用了強化壁面處理。當計算網格足夠密，可以直接求解黏性底層時，近壁面采用適用于低雷諾數的一方程Wolfstein湍流模型，否則使用壁面函數計算。

1.2 物性計算方法

超臨界狀態下流體的物性隨著壓力和溫度發生劇烈變化，而流體物性變化與其裂解吸熱/流動傳熱過程是緊密耦合在一起的，因而物性的準確計算對超臨界壓力碳氫燃料裂解與傳熱的研究十分關鍵。修正的對應態(Corresponding-State) 方法[23-24]是計算流體混合物密度、導熱系數和黏性系數的普適方法。選擇丙烷作為參考物質，采用修正的對應態方法計算混合物密度和輸運系數。流體的焓值和定壓比熱通過基本的熱力學關系式以及Soave-Redlich-Kwong(SRK) 狀態方程計算得到[25]。對于質量擴散系數的計算，首先采用Fuller經驗公式計算低壓下的二元質量擴散系數，然后再通過 Takahashi建議的對比態方法來考慮壓力的影響[26]。各物性的詳細計算方法及其可靠性驗證可參考文獻[17, 27]。

1.3 化學動力學模型

碳氫燃料在高溫條件下發生裂解反應，高分子碳氫燃料的裂解反應的詳細機理非常復雜，涉及成百個基元反應和上千種組分，以目前的計算條件采用詳細機理進行化學反應流動模擬非常困難，因此進行數值模擬通常采用簡化的反應機理。本文選擇目前使用較為廣泛的一步總包化學反應模型。Ward等[14]提出的PPD化學模型，適用于壓力在3.45～11.38 MPa范圍內的輕度裂解。根據實驗結果和質量守恒原理得到總包化學反應機理為[22, 27]

C10H22→0.153CH4+0.222C2H4+0.138C2H6+

0.200C3H6+0.185C3H8+0.171C4H8+

0.118C4H10+0.149C5H10+0.137C5H12+

0.170C6H12+0.106C6H14+0.147C7H14+

0.091C7H16+0.132C8H16+0.040C8H18+

0.046C9H18+0.031C9H20

該反應速率常數由Arrhenius公式kA=A·exp(-Ea/RT)計算，其中指前因子A=1.6×1015s-1，活化能Ea=263.7 kJ/mol，R為普適氣體常數。

1.4 數值格式與收斂準則

以上熱物性計算方法以及化學動力學模型通過用戶自定義函數(User Defined Function, UDF)編程的方式建立在商用計算流體力學(CFD)軟件ANSYS FLUENT 13.0中。在本文數值模擬中，對流項離散采用二階迎風格式，黏性項采用中心差分格式，壓力-速度耦合采用Coupled算法。控制方程求解收斂判斷條件為方程殘差<10-5，同時監控進出口流量、出口溫度、速度、重要組分質量分數及壓力值變化直至其趨于穩定。

2 快速算法的構建

基于以上理論，在前期的工作中已經建立了完整的模擬超臨界壓力碳氫燃料裂解與傳熱的數值方法[17]，并成功用于超臨界壓力正癸烷裂解吸熱/流動傳熱的模擬研究，充分驗證了算法和程序的可靠性[22, 27]。前期的數值方法包含完整的組分輸運方程，通過各組分源項來考慮化學反應的影響，并且準確考慮了各組分之間的擴散效應。本文在前期算法的基礎上，通過數值分析和理論推導進行算法改進和優化，從而建立一種新的快速算法。

高分子碳氫燃料裂解產物組分很多，求解完整的組分輸運方程給數值模擬帶來很大的挑戰。此外，混合物的物性計算過程非常復雜，而且在CFD求解過程中需要進行多次迭代才能滿足流場收斂條件，其中每次迭代過程中所有控制體內的物性均需要重新進行計算，這必然會消耗大量的時間。本文將分別對這兩方面進行優化和改進以提高計算效率。

2.1 熱物性查表法

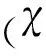
(8)

式中：下標“o”表示物性庫起始點的狀態：po=3 MPa，To=300 K，αo=0；Δp=0.2 MPa；ΔT=2 K；Δα=1%。

CFD求解過程中，通過控制體內的p、T、α和式(8)確定該狀態點在物性庫中對應的位置，再通過線性插值得到物性。需要說明的是，該物性庫存儲僅需要占用大約75 MB內存，對硬件資源需求很小。

為了比較物性查表法與直接計算方法的計算效率，總共計算了2 383 101個狀態的物性：溫度為500～1 200 K, 間隔0.5 K；壓力為3～5 MPa，間隔0.1 MPa；裂解率為0～40%，間隔0.5%。計算所用時間如表1所示。由于直接法需要進行2 383 101次混合物物性求解，而查表法每次計算只需進行線性插值，因此查表法比直接法計算效率有數量級的提升。

表1 熱物性計算時間對比

進一步考察查表法的精度。采用上述各個工況下的計算結果分析查表法的精度，與直接計算結果相比誤差均在±0.4%以內。因此，本文建立的物性庫查表法精度是可以滿足數值模擬需求的。

2.2 組分輸運方程的快速求解方法

2.2.1 組分輸運特性分析

當分子數密度存在空間不均勻性時，由于分子的熱運動或湍流脈動而發生的質量輸運，稱為擴散現象。這種輸運特性由組分輸運方程體現。精確考慮各個組分之間的擴散特性需要求解完整的組分輸運方程[17]。對于混合物組分非常多的情況，這必然會帶來很大的計算開銷。因此，如果能夠建立一種簡單且能保證精度的計算方法，對提高計算效率有非常重要的意義。本節主要分析超臨界壓力下正癸烷裂解反應流動中的組分擴散規律，從而尋找一種簡單有效的組分擴散計算方法，為組分輸運方程的簡化提供依據。

首先選擇圖1所示模型分析超臨界壓力正癸烷裂解產物的組分輸運特性。采用軸對稱模型進行計算。圖中O為坐標原點；x和r分別為軸向和徑向坐標。計算工況為[14]：入口溫度T0=473 K；入口壓力p0的范圍為3.45～11.38 MPa；流量m=0.5 mL/min。壁面溫度Tw沿x方向的變化函數為f(x)，其中最高壁溫Tw_max=873 K。在進行網格無關性驗證后選擇30×1 000網格進行計算。

圖1 計算模型示意圖Fig.1 Schematic of computation model

對于冷卻通道內碳氫燃料裂解反應流動問題，入口處燃料溫度低于裂解發生的溫度，隨著壁面加熱，近壁面燃料溫度首先升高至裂解所需溫度進而發生裂解，從而各組分沿垂直壁面方向產生濃度梯度，發生擴散現象。影響擴散特性的參數為有效擴散系數Di,eff，如式(3)所示。Di,eff由湍流擴散系數μt/ρSct和分子擴散系數Di,m兩部分組成。研究發現湍流區的湍流擴散系數通常在10-6m2/s量級以上，而超臨界碳氫燃料分子擴散系數均在10-7m2/s量級，因此在湍流狀態下，μt/ρSct?Di,m,組分輸運由湍流擴散系數主導，分子擴散系數影響忽略不計[13, 14]。但是在黏性底層組分輸運由分子擴散主導，因此分子擴散的準確計算會直接影響近壁面流場的計算精度。圖2為分子擴散系數隨溫度和壓力的變化特征(圖中黑色實線為溫度等值線)，在液態區域(T<618 K)為10-8m2/s量級，超臨界狀態時為10-7m2/s量級，這與文獻[28]中的結論完全吻合。此外，各組分的分子擴散系數隨溫度的升高而增大，隨壓力的增大而減小。

為了考察黏性底層內的擴散特性，在1.0×10-8～1.0×10-6m2/s范圍內選擇不同分子擴散系數進行數值模擬，并與直接計算分子擴散系數時的模擬結果進行對比。數值研究發現，在該范圍內分子擴散系數對軸線上的計算結果幾乎沒有影響，如圖3(a)、圖3 (b)所示(圖中xi為組元i的摩爾分數；Dij為二元質量擴散系數[17])，進一步說明湍流區分子擴散系數的影響是可以忽略不計的。然而在近壁面黏性底層區域，由于不存在湍流擴散，分子擴散系數直接影響組分輸運能力，如圖3(c)、圖3 (d) 所示。研究發現黏性底層內組分輸運能力和濃度對分子擴散系數是比較敏感的。

考慮到在中輕度裂解條件下正癸烷濃度遠大于其他產物濃度，因此其輸運特性對流場影響最大。此外，各組分擴散系數隨溫度和壓力的變化規律相似(如圖2所示)，因此將各組分擴散系數統一選擇為正癸烷擴散系數，即

Di,m=DC10H22,mi=1～N

(9)

則會減小數值模擬與真實物理過程的誤差，保證各壓力和溫度下近壁面組分擴散的計算精度。

數值模擬時，分別采用簡化計算(式(9))與直接計算兩種方法確定分子擴散系數，得到的壁面處質量分數對比情況如圖4所示。結果表明該簡化計算方法在各個壓力下均可準確模擬出壁面組分濃度，說明采用該方法確定分子擴散系數是合理的，具有較寬的適用范圍。

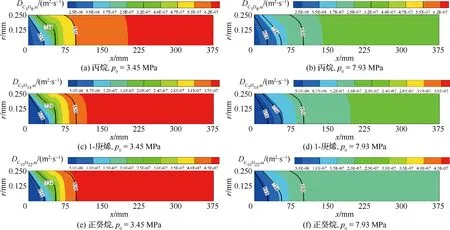
圖2 不同壓力下各組分的分子擴散系數分布Fig.2 Distributions of molecular diffusion coefficients for various species under different pressures

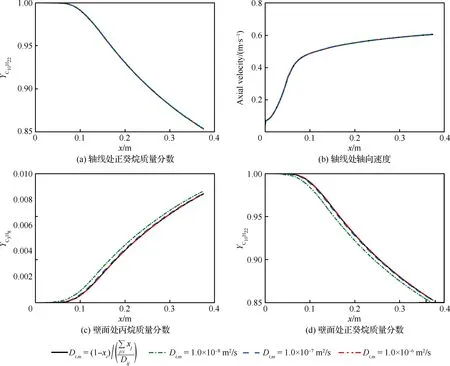
圖3 分子擴散系數對計算結果的影響(p0=3.45 MPa)Fig.3 Effect of molecular diffusion coefficient on simulation results (p0=3.45 MPa)

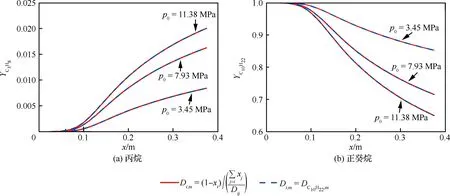
圖4 不同壓力下壁面處組分質量分數Fig.4 Species mass fraction at tube wall under different pressures

2.2.2 組分輸運方程的簡化及其理論基礎

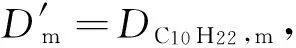
A(Yi)=Si

(10)

式中：算子A的形式為

A=

(11)

如果滿足下列兩個條件：

條件1 對于任意裂解產物a和b，在整個流場域內

(12)

恒成立，其中θ為常數。

條件2 在流場邊界上

(13)

式中：Ω1為入口邊界；Ω2為除入口之外的其他邊界；n為流場邊界外法向；x為求解域空間坐標。

那么組分輸運方程的解必滿足：

Yb=θYa

(14)

其數學證明見附錄A。

對于條件1，由于本文采用一步總包PPD機理，各組分化學反應源項嚴格成比例，因此該條件是成立的。采用CFD技術模擬化學反應流場最為常用的壁面邊界條件為非催化壁面，即?Yi/?n=0;對于冷卻通道內的流動問題，入口邊界上(Ω1)所有裂解產物滿足Yi=0；出口處采用零梯度?Yi/?n=0處理；對于軸對稱或對稱模型，在對稱軸或對稱面上也滿足?Yi/?n=0。因此，對于冷卻通道內的流動問題條件2也是成立的。綜上所述，采用一步總包反應機理模擬冷卻通道內的裂解與流動問題，結論(式(14))是成立的。

根據該結論，只需要求解其中一個產物(例如產物a)的組分輸運方程的解，其他產物(例如產物b)組分輸運方程的解可通過式(14)確定。因此將需要求解的守恒方程數量從24(7+17)個減少到8(7+1)個，必然會大幅度提升計算效率。

3 數值結果與分析

3.1 計算效率和精度分析

基于第2節的理論分析，采用物性查表和組分輸運方程簡化方法，建立了碳氫燃料裂解和對流傳熱分析的快速算法。為了便于比較不同算法的計算效率和精度，本文以STE(Species Transport Equations)、DC(Direct Calculation)和LT(Look-up Table)分別代表組分輸運方程、物性直接計算和物性查表，則“17STE(DC)”代表“17個組分輸運方程(物性直接計算)”方法，即文獻[17]中求解全組分輸運方程的算法，本文稱之為“全組分算法”；“1STE(LT)”代表“1個組分輸運方程(物性查表)”方法，為本文改進和優化后的快速算法。

分別采用兩種算法對文獻[13-14]中的模型(圖1所示)進行計算，以最高壁溫為873 K、質量流量為0.5 mL/min、壓力為3.45 MPa的工況為例，分析不同算法的計算效率。該算例計算硬件為主頻3.6 GHz的臺式機，采用單核進行計算。迭代2 000步流場收斂，計算時間如表2所示。通過對比可以看出，快速算法計算效率比全組分算法提高約22.41倍。計算效率的提高由兩部分組成，其中物性庫查表方法使計算效率提升約3.35倍，而組分輸運方程的簡化使計算效率提升約6.68倍。由于快速算法只需要求解一個組分輸運方程，與混合物組分數量無關，因此該算法對于產物組分越多的裂解反應優勢將會更加明顯。此外，需要說明的是快速算法與全組分算法收斂性一致，在單步迭代計算速度顯著提高的同時，保持了全組分算法的收斂性，并不會增加計算至流場收斂所需的迭代步數。

圖5為快速算法與全組分算法計算的流場內溫度、軸向速度(ux)以及正癸烷質量分數分布對比情況。不同算法計算得到的各參數在近壁面和流場內部均吻合很好，誤差幾乎可以忽略不計。

表2 不同算法的計算時間對比(計算模型見圖1)

Table 2 Comparison of computation time of different algorithms (computation model is illustrated in Fig.1)

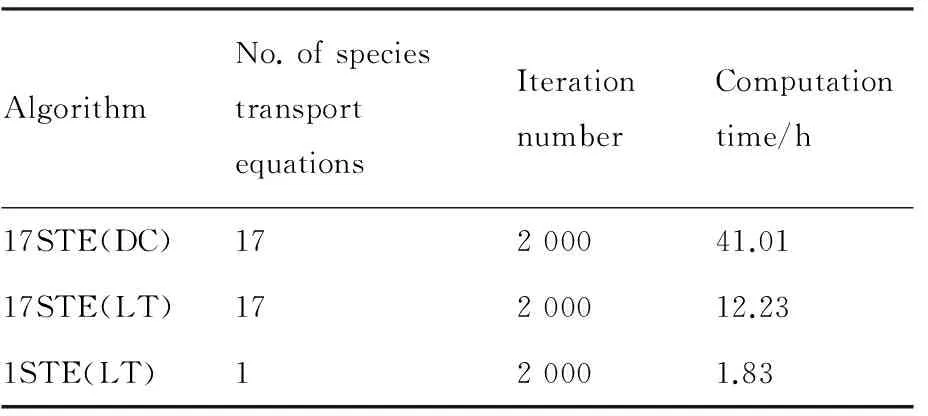
AlgorithmNo.ofspeciestransportequationsIterationnumberComputationtime/h17STE(DC)17200041.0117STE(LT)17200012.231STE(LT)120001.83

此外，快速算法計算得到的正癸烷質量分數和燃料平均溫度與文獻[13-14]中結果的對比情況分別如圖6和圖7所示，相對誤差也均在±0.6%以內。結果表明快速算法在顯著提高計算效率的同時保證了計算精度。

為了進一步考察快速算法的適用范圍，針對壓力為3.45～11.38 MPa，入口流量為0.3～0.7 mL/min的多種工況進行模擬，并與文獻[14]中的數值和實驗結果進行對比。首先比較了不同壓力下流場內熱物性沿流向變化情況，如圖8所示。計算中入口流量為0.3 mL/min，最高壁溫為823 K。各個壓力下熱物性均具有很高的計算精度，相對誤差均在±5%以內。

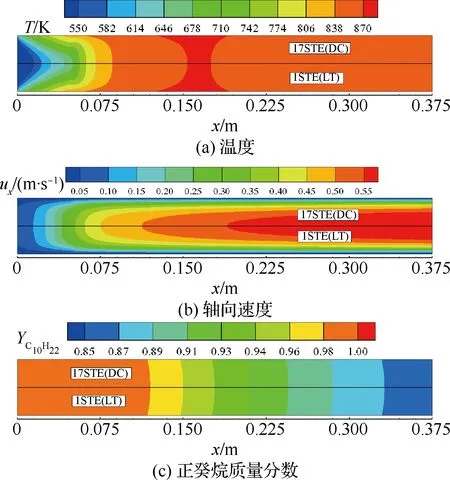
圖5 不同算法計算結果對比(p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K) Fig.5 Comparison of simulation results using different algorithms (p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K)

圖6 軸線上正癸烷質量分數變化 (p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K) Fig.6 Variation of n-decane mass fraction at tube axis (p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K)

在不同壓力和入口流量(0.5、0.7 mL/min)下，計算得到的出口處未裂解正癸烷質量分數與Ward等[14]實驗測量結果對比情況如表3所示。計算時最高壁溫為873 K。當裂解轉換率小于25%時， 計算結果與實驗相對誤差在±1%以內；

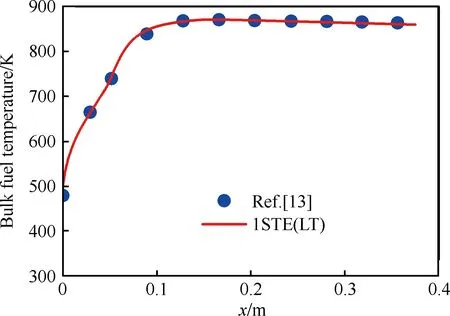
圖7 燃料平均溫度變化 (p0=3.45 MPa,m= 0.5 mL/min, Tw_max=873 K) Fig.7 Variation of bulk fuel temperature (p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K)

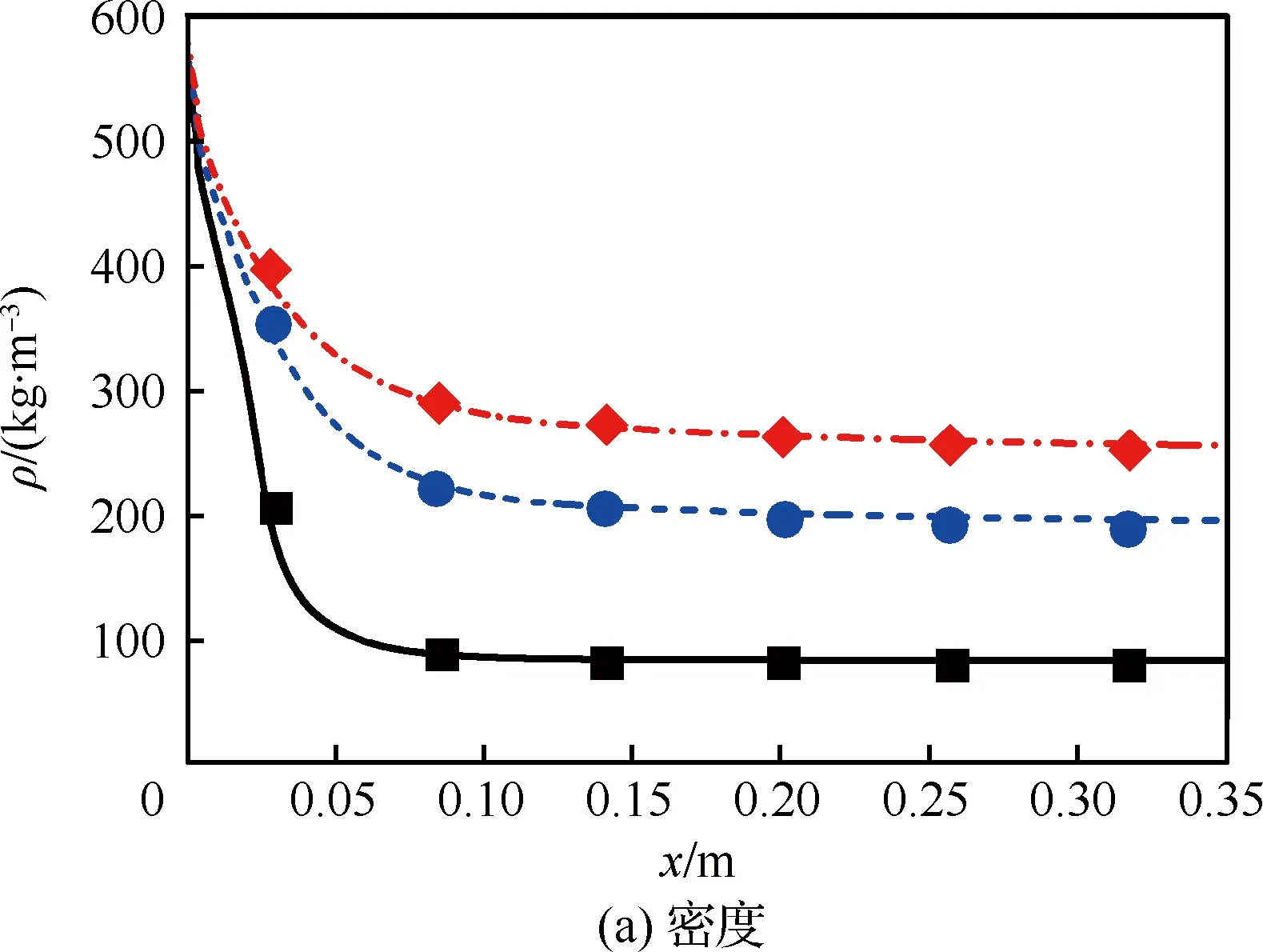
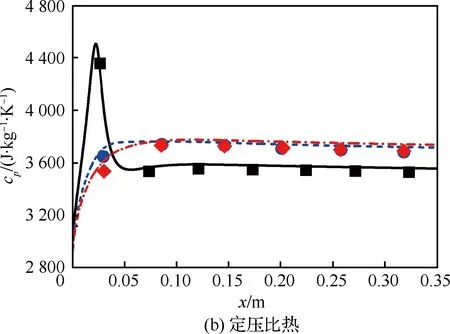
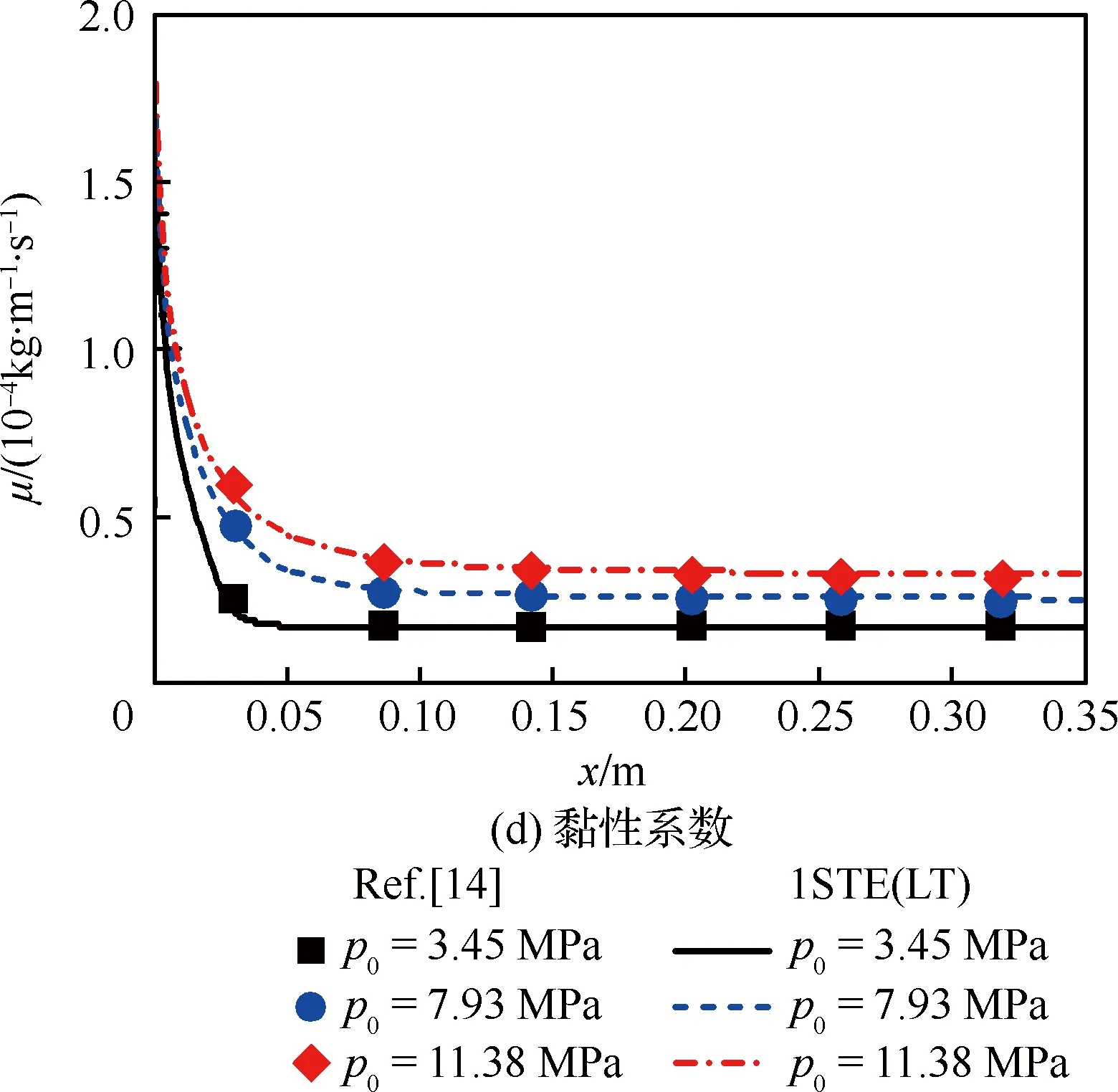
圖8 不同壓力下的熱物性變化(m=0.3 mL/min, Tw_max=823 K) Fig.8 Variation of thermo-physical property under different pressures (m=0.3 mL/min, Tw_max=823 K)

表3 出口處未裂解正癸烷質量分數計算結果與實驗對比

Table 3 Comparison of calculated and experimental results of unreacted n-decane mass fraction at outlet

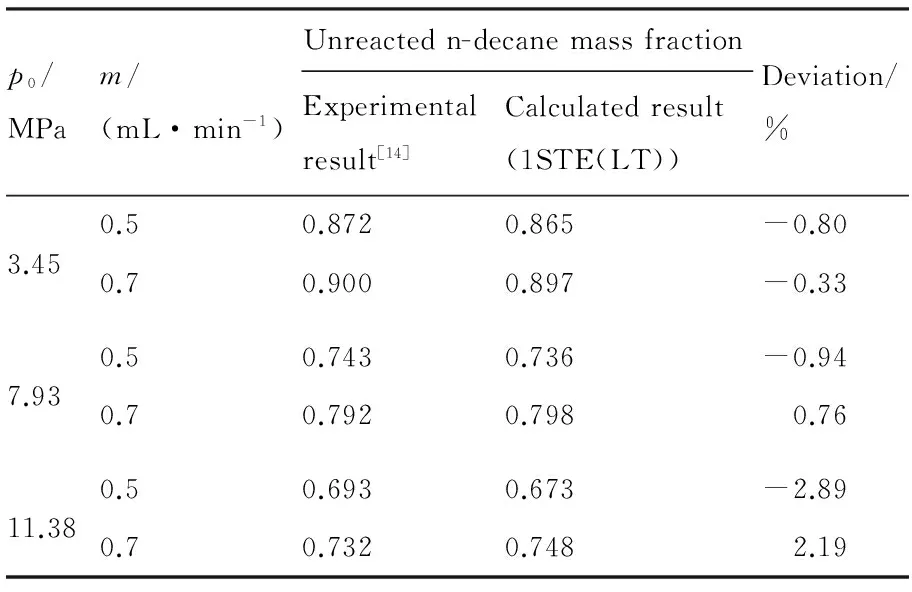
p0/MPam/(mL·min-1)Unreactedn-decanemassfractionExperimentalresult[14]Calculatedresult(1STE(LT))Deviation/%3.450.50.8720.865-0.800.70.9000.897-0.337.930.50.7430.736-0.940.70.7920.798 0.7611.380.50.6930.673-2.890.70.7320.748 2.19

當裂解轉換率達到30%左右時，誤差逐漸增大到±3%。這說明當裂解轉化率大于25%時，開始發生輕微的二次裂解反應，而PPD機理無法考慮二次裂解的影響，因此誤差有所增大。然而在裂解轉化率達到30%時，二次裂解的影響帶來的計算誤差依然較小((3%以內)，因此在數值模擬中仍然可以近似采用PPD機理模擬裂解反應。綜上所示，本文的快速算法適用于壓力為3.45～11.38 MPa、裂解率為0～30%范圍內的正癸烷裂解反應流動的模擬研究。

3.2 矩形截面冷卻通道內傳熱分析

在工程應用中，準確預測超臨界壓力下碳氫燃料在非對稱加熱的矩形截面冷卻通道中的裂解和傳熱特性對超燃沖壓發動機主動冷卻系統的設計非常重要。然而對于三維問題，為了準確捕捉近壁面流場參數的劇烈變化，所需計量網格量巨大。并且，對于含裂解反應的情況，由于混合物組分數量龐大，其計算量是目前開展詳細數值模擬面臨的主要困難。為了考察本文建立的快速算法對實際工程問題的適用性，本文進一步對三維矩形截面冷卻通道非對稱加熱下的裂解反應流動進行模擬，并與已有的算法模擬結果進行比較。

冷卻通道橫截面尺寸為1.5 mm×1.5 mm，加熱段總長300 mm，具體尺寸和計算坐標如圖9所示。為了保證入口邊界層的充分發展并減少出口邊界條件對計算結果的影響，通道前后各取75 mm的絕熱段。正癸烷入口質量流量為4 g/s，入口溫度為700 K，上壁面為均勻熱流qw=2.8 MW/m2，出口壓力為4 MPa。

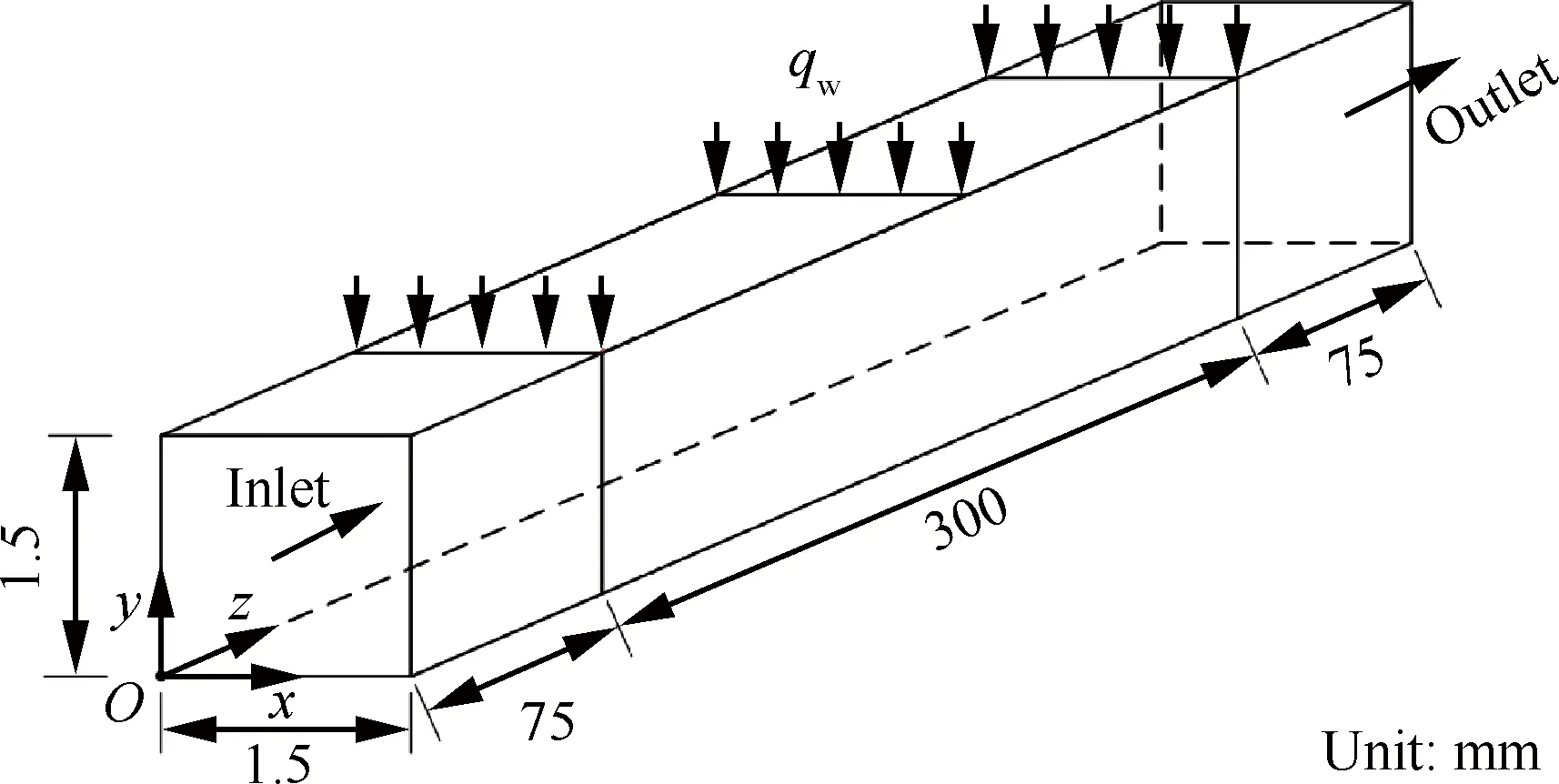
圖9 三維矩形截面冷卻通道示意圖Fig.9 Schematic of 3D rectangular cooling channel

由于問題的對稱性，選取模型的一半進行計算。在數值模擬之前，首先進行了網格獨立性分析。對25×40×700、35×70×1 000、50×80×1 500這3套網格的計算結果進行了比較，發現35×70×1 000的網格已經滿足網格無關性要求，當網格加密到50×80×1 500時，壁面溫度變化在0.3%以內。綜合考慮計算精度和效率，選擇了35×70×1 000的網格進行計算。該算例在HP Z840工作站(處理器為Intel Xeon E5-2687W v4)上進行，各算例均采用40個核心并行計算。

表4為兩種算法各迭代2 000步所用的時間對比。與前文中單核計算效率相近，快速算法將計算效率提高約20倍。

表4 不同算法的計算時間對比(計算模型見圖9)

Table 4 Comparison of computation time of different algorithms (computation model is illustrated in Fig.9)

AlgorithmIterationnumberComputationtime/h17STE(DC)2000300.411STE(LT)200015.33

圖10和圖11給出了加熱段各橫截面(Oxy平面，坐標與圖9對應)溫度以及z向速度(uz)的分布。可以看出快速算法與全組分算法計算結果完全一致。由于熱量從加熱壁面不斷傳入，沿著流動方向，流體溫度不斷升高，密度下降，因而速度逐漸增大。由于熱流集中在冷卻通道的上壁面，因此速度最大的區域也逐漸向上壁面處移動。圖10顯示流體溫度在上壁面與側壁面的交界處(x=0)達到最大值，其主要原因是該處主流速度較小(見圖11)，對流傳熱效果較差。

與圓管中的裂解和流動傳熱現象相比，流體在非對稱加熱的矩形冷卻通道中的流動具有明顯的三維特征。對于非對稱加熱矩形通道，上壁面熱流集中使近壁面出現很高的溫度梯度。溫度越高裂解反應速率越快，而且近壁面流體流速低，滯留時間長，導致近壁面流體裂解轉化率明顯高于其他區域，形成很大的濃度梯度，尤其是在上壁面拐角處，如圖12所示。組分濃度在近壁面的嚴重不均勻性使得擴散現象更加明顯，其中裂解產物逐漸向通道內部擴散，同時未裂解正癸烷向近壁面擴散。

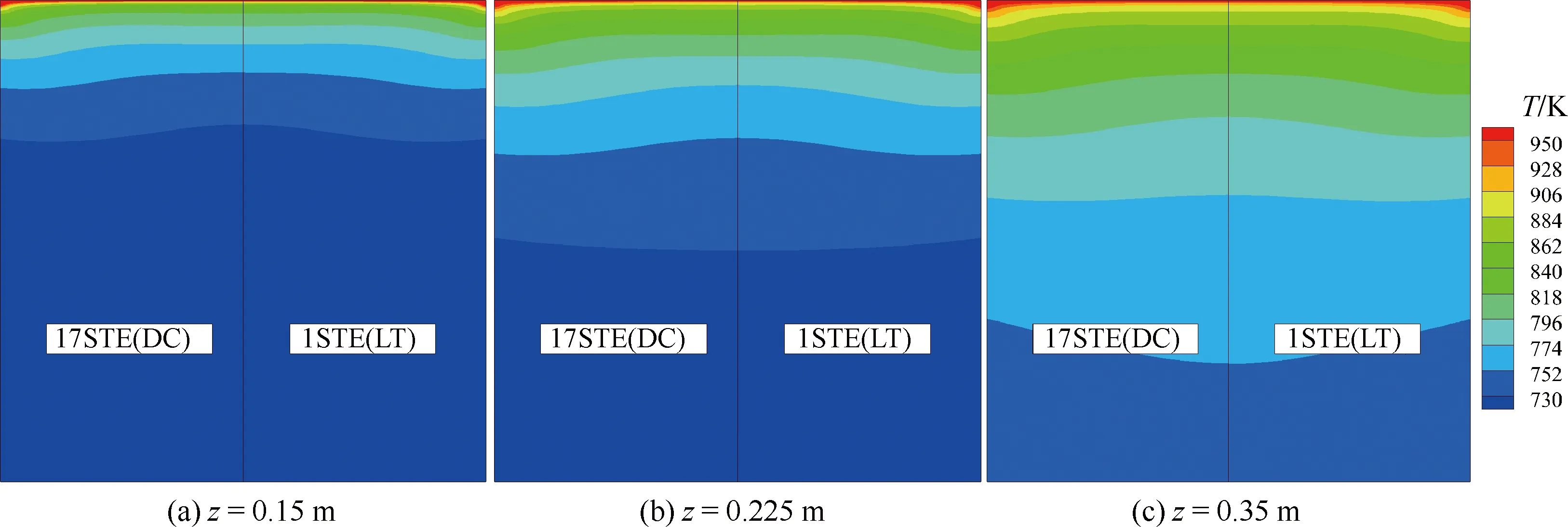
圖10 不同橫截面溫度分布Fig.10 Temperature distribution at different cross-sections

圖11 不同橫截面速度分布Fig.11 Velocity distribution at different cross-sections

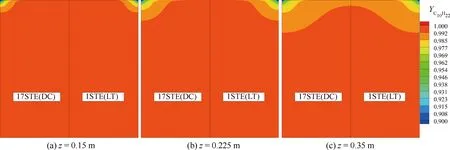
圖12 不同橫截面正癸烷質量分數分布Fig.12 n-decane mass fraction distribution at different cross-sections

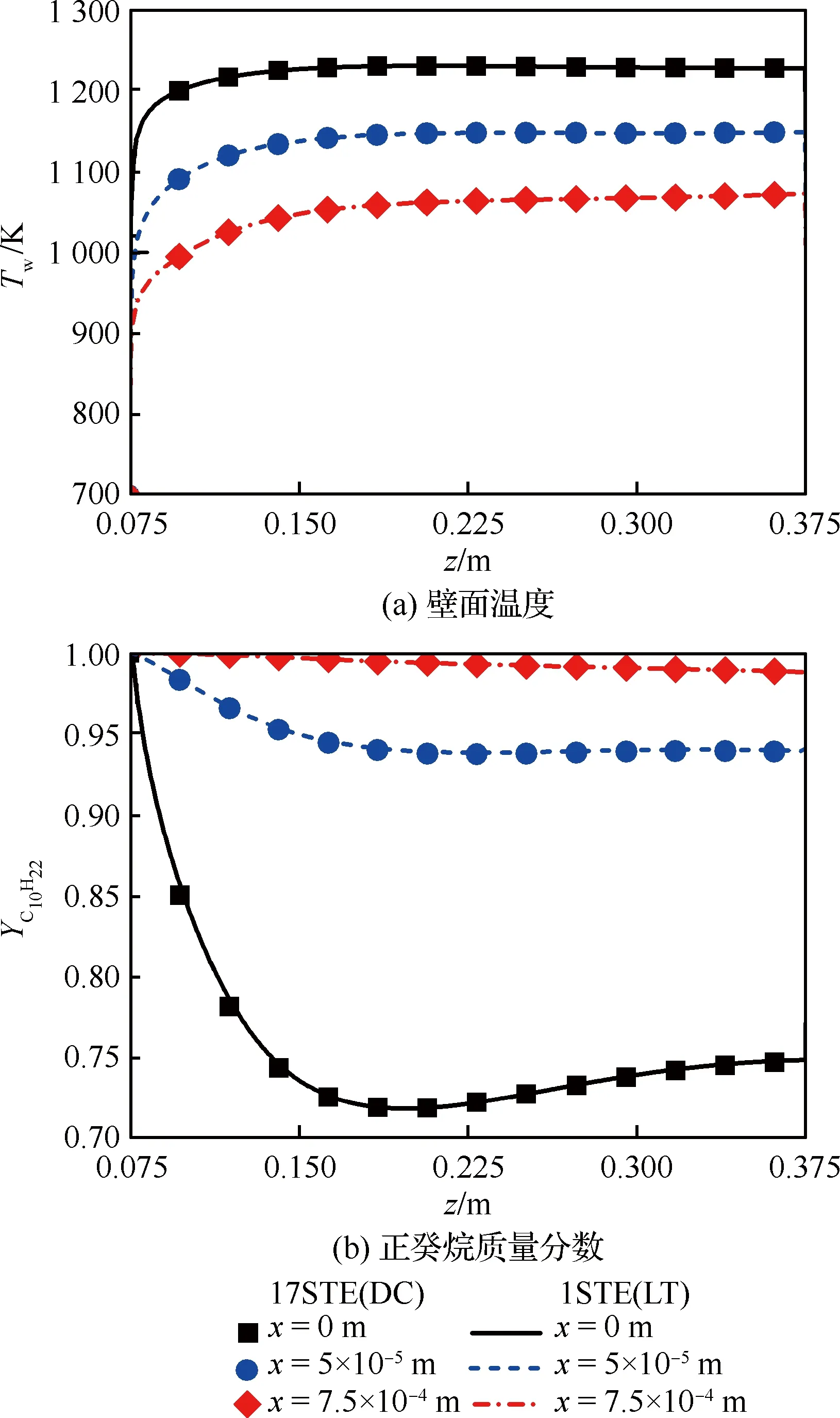
圖13 加熱面不同位置壁面溫度和正癸烷質量 分數變化 Fig.13 Variation of wall temperature and n-decane mass fraction at different positions of heated wall

圖13為上壁面不同位置(x=0、5×10-5、7.5×10-4m，與圖9所示坐標對應)的壁面溫度和正癸烷質量分數沿流向變化情況。與全組分算法計算結果相比，快速算法的壁面溫度相對誤差在±0.1%以內，正癸烷質量分數相對誤差在±0.5%以內。考慮到近壁面黏性底層內組分濃度梯度很大，且組分輸運由分子擴散主導，因此分別假定兩個常數形式的分子擴散系數(Di,m=4.0×10-7、7.0×10-7m2/s)進行模擬，用以研究黏性底層內分子擴散特性對組分濃度的影響。研究表明，在黏性底層組分濃度對分子擴散系數非常敏感，如圖14所示。然而本文建立的分子擴散系數簡化算法(式(9)，與圖14中1STE(LT)對應)具有良好的計算精度，與直接計算分子擴散系數的全組分算法結果(17STE(DC))非常吻合。綜上所述，該快速算法對于三維問題具有很好的適用性，可以精確捕捉流場的細微特征，具有工程應用價值。

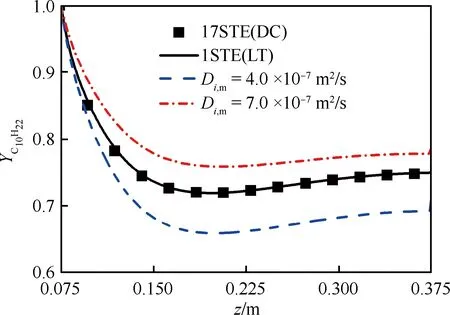
圖14 分子擴散系數對壁面正癸烷質量分數 分布的影響(x=0) Fig.14 Effect of molecular diffusion coefficient on n-decane mass fraction distribution at wall (x=0)

4 結 論

1) 本文建立的快速算法采用查表法計算裂解混合物的物性，并且將需要求解的組分輸運方程由N-1個簡化為1個。

2) 與全組分算法相比,快速算法計算效率提升了約20倍，同時還保留了全組分算法的計算精度。

3) 該算法適用于壓力在3.45～11.38 MPa范圍內的正癸烷輕度裂解與傳熱問題。當裂解率小于25%時，正癸烷質量分數的計算結果與實驗數據相對誤差在±1%以內；當裂解率達到30%左右時，誤差在±3%以內。

4) 近壁面黏性底層內的裂解轉化率和組分分布對分子擴散系數非常敏感，本文建立的分子擴散系數簡化算法在不同壓力和溫度下均具有良好的計算精度。

5) 該算法能夠快速、準確地模擬三維冷卻通道內正癸烷裂解吸熱與流動傳熱問題，具有良好的工程應用價值。

[1] POWELL O A, EDWARDS J T, NORRIS R B, et al. Development of hydrocarbon-fueled scramjet engines: The hypersonic technology (HyTech) program[J]. Journal of Propulsion and Power, 2001, 17(6): 1170-1176.

[2] BAO W, LI X, QIN J, et al. Efficient utilization of heat sink of hydrocarbon fuel for regeneratively cooled scramjet[J]. Applied Thermal Engineering, 2012, 33(1): 208-218.

[3] EDWARDS T. Cracking and deposition behavior of supercritical hydrocarbon aviation fuels[J]. Combustion Science & Technology, 2006, 178(1-3): 307-334.

[4] BAO W, ZHANG S, QIN J, et al. Numerical analysis of flowing cracked hydrocarbon fuel inside cooling channels in view of thermal management[J]. Energy, 2014, 67(4): 149-161.

[5] HUANG H, SOBEL D R, SPADACCINI L J. Endothermic heat-sink of hydrocarbon fuels for scramjet cooling: AIAA-2002-3871[R]. Reston, VA: AIAA, 2002.

[6] 俞剛， 范學軍. 超聲速燃燒與高超聲速推進[J]. 力學進展, 2013, 43(5): 449-471.

YU G, FAN X J. Supersonic combustion and hypersonic propulsion[J]. Advances in Mechanics, 2013, 43(5): 449-471 (in Chinese).

[7] ZHONG Z, WANG Z, SUN M. Effects of fuel cracking on combustion characteristics of a supersonic model combustor[J]. Acta Astronautica, 2015, 110: 1-8.

[8] FAN X, YU G, LI J, et al. Combustion and ignition of thermally cracked kerosene in supersonic model combustors[J]. Journal of Propulsion and Power, 2007, 23(2): 317-324.

[9] ZHONG F Q, FAN X J, YU G, et al. Thermal cracking and heat sink capacity of aviation kerosene under super critical conditions[J]. Journal of Thermophysics & Heat Transfer, 2011, 25(6): 1226-1232.

[10] ZHONG F Q, FAN X J, YU G, et al. Thermal cracking of aviation kerosene for scramjet applications[J]. Science in China Series E: Technological Sciences, 2009, 52(9): 2644-2652.

[11] JIANG R, LIU G, ZHANG X. Thermal cracking of hydrocarbon aviation fuels in regenerative cooling microchannels[J]. Energy & Fuels, 2013, 27(5): 2563-2577.

[12] STEWART J, BREZINSKY K, GLASSMAN I. Supercritical pyrolysis of decalin, tetralin, and n-decane at 700-800K: Product distribution and reaction mechanism[J]. Combustion Science & Technology, 1998, 136(1-6): 373-390.

[13] WARD T, ZABARNICK S, ERVIN J, et al. Simulations of flowing mildly-cracked normal alkanes incorporating proportional product distributions[J]. Journal of Propulsion and Power, 2004, 20(3): 394-402.

[14] WARD T A, ERVIN J S, ZABARNICK S, et al. Pressure effects on flowing mildly-cracked n-decane[J]. Journal of Propulsion and Power, 2005, 21(2): 344-355.

[15] ZHU Y, LIU B, JIANG P. Experimental and numerical investigations on n-decane thermal cracking at supercritical pressures in a vertical tube[J]. Energy & Fuels, 2013, 28(1): 466-474.

[16] XU K, MENG H. Analyses of surrogate models for calculating thermophysical properties of aviation kerosene RP-3 at supercritical pressures[J]. Science in China Series E: Technological Sciences, 2015, 58(3): 510-518.

[17] 阮波，孟華. 碳氫燃料裂解吸熱反應及超臨界傳熱現象數值模型的構建與驗證[J]. 航空學報, 2011, 32(12): 2220-2226.

RUAN B, MENG H. Numerical model development and validation for hydrocarbon fuel supercritical heat transfer with endothermic pyrolysis[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(12): 2220-2226 (in Chinese).

[18] ZHANG S, FENG Y, JIANG Y, et al. Thermal behavior in the cracking reaction zone of scramjet cooling channels at different channel aspect ratios[J]. Acta Astronautica, 2016, 127: 41-56.

[19] FENG Y, JIANG Y, LI X, et al. Numerical study on the influences of heat and mass transfers on the pyrolysis of hydrocarbon fuel in mini-channel[J]. Applied Thermal Engineering, 2017, 119: 650-658.

[20] 劉志琦. 超燃沖壓發動機主動冷卻通道內的超臨界流動與傳熱過程數值模擬[D]. 長沙： 國防科學技術大學, 2015: 18-26.

LIU Z Q. Numerical simulation of flow and heat transfer in cooling channels of active cooled scramjet engines[D]. Changsha: National University of Defense Technology, 2015: 18-26 (in Chinese).

[21] 程澤源， 朱劍琴. 低裂解度正癸烷物性快速計算方法[J]. 推進技術, 2016, 37(8): 1586-1593.

CHENG Z Y, ZHU J Q. Fast calculation method on physical properties in mild cracking of decane[J]. Journal of Propulsion Technology, 2016, 37(8): 1586-1593 (in Chinese).

[22] RUAN B, MENG H, YANG V. Simplification of pyrolytic reaction mechanism and turbulent heat transfer of n-decane at supercritical pressures[J]. International Journal of Heat and Mass Transfer, 2014, 69(2): 455-463.

[23] ELY J F, HANLEY H. Prediction of transport properties: 1. Viscosity of fluids and mixtures[J]. Industrial & Engineering Chemistry Fundamentals, 1981, 20(4): 323-332.

[24] ELY J F, HANLEY H. Prediction of transport properties: 2. Thermal conductivity of pure fluids and mixtures[J]. Industrial & Engineering Chemistry Fundamentals, 1983, 22(1): 90-97.

[25] MENG H, YANG V. A unified treatment of general fluid thermodynamics and its application to a preconditioning scheme[J]. Journal of Computational Physics, 2003, 189(1): 277-304.

[26] MENG H, HSIAO G C, YANG V, et al. Transport and dynamics of liquid oxygen droplets in supercritical hydrogen streams[J]. Journal of Fluid Mechanics, 2005, 527: 115-139.

[27] 阮波. 超臨界壓力下正癸烷裂解吸熱和對流傳熱現象的數值模擬研究[D]. 杭州： 浙江大學, 2013: 40-61.

RUAN B. Numerical studies of convective heat transfer of n-decane with endothermic pyrolytic reaction at supercritical pressures[D]. Hangzhou: Zhejiang University, 2013:40-61 (in Chinese).

[28] STEWART J F. Supercritical pyrolysis of the endothermic fuels methylcyclohexane, decalin, and tetralin[J]. Dissertation Abstracts International, 1999, 60(9): 4852-5119.

附錄A：

已知方程組

(A1)

假設Sb=θSa在整個求解域中恒成立，求證：方程組(A1)的解滿足Yb=θYa。

證明：根據上述偏微分方程和定解條件可知式(A1)為定解問題，解是唯一的。

對其中任意產物組分a和b，若Sb=θSa,則有

(A2)

根據微分算子性質有A(θYa)=θA(Ya)=θSa,再根據定解條件可得：

(A3)

即Yb和θYa分別滿足式(A2)和式(A3)中的偏微分方程和定解條件。由于式(A2)和式(A3)中的方程和定解條件完全相同，根據解的唯一性可知Yb=θYa。

證明完畢。