基于三維離散法翻轉混合設備顆粒的運動行為模擬研究

張凱杰

許 薔

王 滔

(南京林業大學機械電子工程學院，江蘇 南京 210037)

顆粒混合被視為一個非常復雜的過程，混合介質、混合設備、所處的環境和因素都會影響到混合的具體過程[1]。翻轉混合設備是混合物料加工生產中的主要設備之一，其內部的攪拌過程和混勻特性對混合效率有著很大的影響。在顆粒混合方面，通常研究的是不同屬性顆粒在混勻過程中出現的分離或者離析現象[2]。趙拉拉等[3]利用離散元的方法研究了不同形狀顆粒的粒度對分層速度的影響規律，該規律屬于巴西果效應。王娜娜等[4]利用PIV無接觸測量技術研究了玉米秸稈和陶瓷球混合顆粒在豎直管內的運動規律，得出了混合顆粒的軸向速度呈拋物線狀分布。陳瓊等[5]通過直剪試驗和離散元模擬，發現在玻璃-橡膠混合顆粒隨著橡膠顆粒的增加, 會出現剪脹到剪縮的相轉變現象，且混合顆粒固體的彈性有了很大的提高。

近年來，離散元方法在顆粒混合領域取得了可觀的發展。眾多學者利用離散元仿真建模的方法研究了不同因素下的混合效果。Guo等[6]利用離散單元法在流化床預測高縱橫比顆粒的破碎，研究表明，顆粒的破碎率取決于施加的壓力、葉片的旋轉速度、內部顆粒之間的摩擦以及顆粒和壁面之間的摩擦。張濤等[7]利用離散元仿真得到了種群運動規律，并利用臺架試驗驗證了排種性能較好的種群運動規律。此外，Wu等[8]通過離散元方法研究了離散顆粒層被橫向推移過程的力學行為，得出了推移力的變化呈現線性上升和指數上升2個階段。Lemieux 等[9]通過對一種復雜混合器的離散元模擬，研究表明混合率隨著混合速度的增加呈現先降低后增加的趨勢。

本研究擬在現有雙錐反轉出料混合機的基礎上進行研究，通過混合機工作過程的離散化虛擬試驗，來探究顆粒翻轉運動行為及其對混合度的影響規律。

1 離散單元模型

翻轉混合設備在攪拌時，低葉片將物料推向進料側，高葉片將物料推向出料側；推向進料側的物料被進料錐擋回攪拌筒，推向出料側的物料被出料錐和出料葉片背面鋼板擋住折回攪拌筒，葉片的布置方式使得顆粒除了提升、自落之外，軸向竄動比較劇烈[10]。采用離散仿真軟件EDEM來分析翻轉混合設備攪拌過程的顆粒運動情況，不僅可以研究該設備的混合性能及影響混合的參數，還能為優化翻轉混合設備提供依據。

1.1 接觸模型

混合顆粒過程的實質是通過攪拌葉片的齒面與顆粒之間，以及顆粒與顆粒之間的接觸、碰撞來實現能量的傳遞，最終促成顆粒群的運動、達到混合機內物料精確和均勻分布的目的。為正確描述顆粒與葉片表面以及顆粒與顆粒之間的碰撞過程，顆粒的離散元研究常常采用彈性-阻尼-摩擦接觸力學模型[11-14]，見圖1。

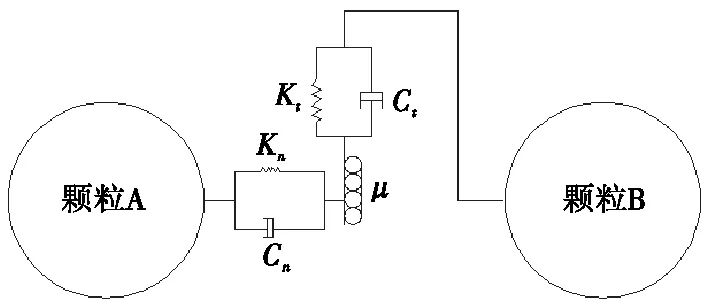
圖1 接觸力學模型Figure 1 Contact mechanical model

通過接觸力學的分析，可以得到：

(1)

(2)

Ft=-Stδt，

(3)

(4)

(5)

(6)

(7)

式中：

Fn——法向力，N；

Ft——切向力，N；

Sn——法向剛度，MPa/cm；

St——切向剛度，MPa/cm；

β——阻尼系數；

R*——等效顆粒的半徑，m；

Y*——等效楊氏模量，Pa；

δn——法向疊合量，m；

m*——等效質量，kg；

e——恢復系數；

G*——等效剪切模量，MPa。

1.2 幾何模型

本試驗模擬非等粒徑顆粒在翻轉混合設備不同轉速條件下的翻轉運動及混合行為。

翻轉設備的結構見圖2。翻轉筒體可分為進料錐筒1、圓柱筒2和出料錐筒3。攪拌葉片由高低錯位等間距排列的4個錐狀葉片4組成。

圖2 翻轉設備的結構Figure 2 The structure of rotary device

1.3 顆粒模型

本試驗模擬的顆粒原型為糙米籽粒，外觀形態為橢球狀。多次測量后得到顆粒的長軸為7.5 mm，短軸為5 mm。在離散商業軟件EDEM中采用球形顆粒進行填充，為簡化方便計算，采用球體顆粒進行糙米顆粒的填充，球形顆粒為其余營養物質。模擬顆粒的模型見圖3。仿真時，顆粒與翻轉設備的參數見表1[15]，仿真時間為30 s。

2 仿真試驗和結果分析

圖4為翻轉混合設備混合的工作過程，本模擬試驗采用Hertz-Mindlin(no slip)模型進行低轉速下的兩類顆粒群在4個錐狀葉片下的運動仿真，其中顆粒的數量定為4 125個，兩類顆粒從X軸負上的重力方向下落。為了便于分析顆粒翻轉運動及混合程度，將等粒徑的同屬性橢球狀顆粒和球形顆粒在初始狀態下標定為綠、白色兩類，谷粒2 326個，營養物質顆粒為1 799個，在ZX平面上，以Z軸向左為正方向，以X軸向上為正方向，混合葉片以順時針方向轉動。混合葉片的5種轉速為：10，20，30，40，50 r/min。顆粒混合過程中會發生一系列復雜的運動。仿真前0.5 s為顆粒對流混合階段[圖4(a)]，0.5 s[圖4(b)]后開始對流、剪切混合，到達5 s時為剪切混合階段，即糙米和營養物質顆粒進行大規模、大尺度的相對混合，使得顆粒之間在攪拌桶內快速交錯運動；30 s[圖4(c)]時對流混合階段達到了相對穩定狀態，此時，屬于擴散混合階段，最終兩顆粒群混合均勻。

圖3 糙米和顆粒模型Figure 3 Brown rice and particle model

表1 模擬所需參數Table 1 The required parameters of simulation

圖4 翻轉混合設備混合的工作過程Figure 4 The working process of rotary device

2.1 顆粒翻轉運動行為分析

為了確定顆粒的翻轉運動，隨機提取5種轉速下單顆粒在轉筒軸向的運動坐標，并做出顆粒在軸向方向上的運動軌跡圖，見圖5。筒體內的顆粒受到剪切、分流、擠壓、拉伸和集聚復合作用。所以，5種轉速下的顆粒都在做翻轉運動，轉速的增加有利于增強顆粒軸向運動的隨機性，降低了顆粒的集中現象，但是現象不是很明顯，與王瑞芳等[16]研究的單顆粒運動結果相符。由圖5可知，隨著轉筒的轉動而被提升的顆粒，當被提升到一定的高度后在重力和擠壓力的作用下，以一定的速度下落，下落顆粒的運動軌跡呈空間曲線型，這與黃志剛等[17]在研究轉筒干燥器內顆粒物料運動相符。該5種轉速下的混合是從顆粒群的對流混合狀態到擴散混合狀態的逐漸演變過程。如圖6所示，從單顆粒在5種不同轉速下的軸向運動軌跡可以發現，左下角與葉片接觸的顆粒運動呈現空間曲線規律，轉速的增加有利于加劇顆粒群之間的軸向隨機運動，軸向混合效果就越好。隨著翻轉混合的持續，顆粒群運動軌跡也呈空間曲線分布。

2.2 顆粒混合研究

從對顆粒群在不同轉速下運動矢量的結果看，在混合初期，2種顆粒群隨時間基本是整體遷移，30 s時兩體系都達到了擴散混合階段，靠近葉片的顆粒在該區域內呈現一條空間曲線狀，這和高紅利等[18]在薄滾筒內研究二元濕顆粒體系混合行為離散單元模擬干濕顆粒界面形成的軌跡宏觀上一致。而由顆粒翻轉運動分析結果發現，轉速的增加有利于顆粒群的軸向混合。為了定量描述轉速和混合度的關系，采用標準差來反映混合度，為了得到顆粒在各個時間段內的標準差，在幾何體YZ面內劃分了8×4個網格，如圖7所示，每一個網格都是一個樣本，每一個樣本寬為40 mm，厚為18 mm。但是，由于每一個樣本內的顆粒數量相差很大，在翻轉設備的上半部分，樣本網格可能不含顆粒，因此采用了加權方案來解決這一問題，即含有較多顆粒的樣本具有較大的權重，而含有較少顆粒的樣本所占的權重較少，如果網格內沒有顆粒，那么權重為零。在此原則上，可求得兩類顆粒的標準差。

圖5 單顆粒在5種不同轉速下的軸向運動軌跡Figure 5 The axial movement of the single particle at five different speeds

圖6 顆粒群在不同轉速下運動矢量Figure 6 Particle group moving vector at different speeds

(8)

式中：

S——標準差；

n——試驗的樣本總數；

xi——任一樣本中某指定成分的含量，

x0——所有樣本中某中指定成分含量的算術平均值。

根據提取顆粒樣本數量，利用Matlab繪制出了翻轉混合設備的時間與混合度的關系曲線，見圖8。

圖8中可以明顯地發現，5種轉速下的曲線規律幾乎相同。混合過程中的標準偏差是不斷減少的，S越小表示混合效果越好。在10 r/min時，前8 s的混合效果很差，因為此時轉速較低，在對流混合和剪切混合的相互作用下，混合不穩定。隨著時間的變化，混合效果明顯，在30 s時趨于穩定；20～50 r/min下混合度的變化逐漸減小，在30 s時趨于平穩。分析其原因，兩類顆粒在葉片的攪動下，對流混合較為明顯，顆粒都進行了大規模的相對運動，致使顆粒在空間快速交錯混合；而當接近20 s時，存在對流、剪切混合，使得顆粒在運動過程中形成剪切面，顆粒流不斷被減薄，實現位置的相互變換混合。所以，這樣周期性的翻轉運動相交錯，將混合度逐漸降低至某一定值。

圖7 在幾何體YZ面內劃分了8×4個網格劃分圖Figure 7 8×4 cell division diagram of geometry in YZ plane

圖8 不同轉速下混合度隨時間的變化Figure 8 The mixing degree varies with time

明確了翻轉筒體軸向混合度和轉速的變化趨勢后，為了建立數學模型，采用MATLAB數據處理軟件中的Exponential模型[2]擬合了5種轉速下混合度與轉速的數學關系。數學模型為：

S=a×exp(b×x)+c×exp(d×x)，

(9)

式中：

S——標準差；

x——翻轉筒體的轉速，r/min；

a,b,c,d——分別是模型系數，具體值見表2。

表2不同轉速下數學模型的參數
Table 2 Mathematical model parameters of the relationship between standard deviation and speed

通過表2可以發現，各轉速下采用數學模型[式(9)]擬合后的方程決定系數R2值都接近1，方程的擬合優度都比較好，表明該模型能很好地表示混合度和轉速的定量關系。采用標準差±均值計算模型參數的范圍[19]，最終統一后標準差與轉速的表達式為：

S=(-0.28～0.97)×exp[(-0.009～0.05)×x]+(0.14～0.50)×exp[(0.49～1.58)×x]。

(10)

由圖9可知，在轉速為10 r/min的情況下，翻轉混合設備的混合誤差為5.846%，接近理想誤差水平，這與實際工況下轉速相一致。

圖9 轉速與混合誤差關系曲線Figure 9 Speed and mixed error relationship curve

式(10)可以用來指導翻轉混合設備提高混合效率，圖9用來控制速度的界限范圍。根據所需要的混合要求，來控制翻轉設備的轉速達到預期的混合效果，同時該研究為針對設計離散混合物料的相關領域提供了思路和方法。

3 結論

本研究采用三維離散單元法研究了5種轉速下翻轉混合設備內非等粒徑的2種軸向分層顆粒的運動行為，并利用標準差來衡量翻轉混合設備的混合行為以及采用混合誤差來提取最佳轉速，同時建立轉速和混合度的數學模型。

(1) 從顆粒翻轉運動分析上發現,顆粒在回轉設備內主要通過拋擲運動向軸向方向混合，其拋擲運動是一個動態變化曲線，呈空間曲線分布規律。

(2) 回轉設備的速度對混合的影響很大，速度過大會使擴散混合過程不穩定，導致實際混合度偏離最佳混合范圍，混合誤差過大不利于充分混合。

(3) 離散單元法能較好地模擬回轉設備顆粒混合行為，預測出最佳混合的設備轉速。

[1] 周志勇.基于DEM的強力混合機混勻過程模擬及結構優化[D].湘潭: 湘潭大學, 2014: 5-6.

[2] 劉揚, 韓燕龍, 賈富國, 等.橢球顆粒攪拌運動及混合特性的數值模擬研究[J].物理學報, 2015, 64(11): 1-2.

[3] 趙啦啦, 劉初升, 閆俊霞, 等.顆粒分層過程三維離散元法模擬研究[J].物理學報, 2010, 59(3): 1 870-1 871.

[4] 王娜娜, 易維明, 楊延強, 等.豎直管內陶瓷球和玉米秸粉混合顆粒運動的PIV測量[J].農業工程學報, 2008, 24(3): 155-156.

[5] 陳瓊, 王青花, 趙闖, 等.玻璃-橡膠混合顆粒的力學響應研究[J].物理學報, 2015, 64(15): 1-4.

[6] GUO Y, WASSGREN C, HANCOCK B, et al.Predicting breakage of high aspect ratio particles in an agitated bed using the Discrete Element Method[J].Chemical Engineering Science, 2016, 10(43): 314-327.

[7] 張濤, 劉飛, 趙滿全, 等.基于離散元的排種器排種室內玉米種群運動規律[J].農業工程學報, 32(22): 27-28.

[8] 吳迪平, 李星祥, 秦勤, 等.離散顆粒層被橫向推移過程中的力學行為研究[J].物理學報, 2014, 64(9): 1-2.

[9] LEMIEUX M, LEONARD G, DOUCET J, et al．Large-scale numerical investigation of solids mixing in a V-blenderusing the discrete element method[J].Powder Technology, 2008, 181: 205-216．

[10] 馮忠緒.混凝土的攪拌過程及其模擬[J].西安公路交通大學學報, 1997, 12(4): 1-2.

[11] LI J, WEBB C, PANDIELLA S, et al.Discrete particle motion on sieves-a numerical study using the DEM simulation[J].Powder Technology, 2003, 133: 190-202.

[12] PAUL W C, MARK L S.DEM modelling of industrial granular flow: 3D case studies and the effect of particle shape on hopper discharge[J].Appled Mathematical Modelling, 2002, 26: 89-111.

[13] TIJSKENS E, RAMON H, BAERDEMAEKER J D.Discrete element modelling for process simulation in agriculture[J].Journal of Sound and Vibrition, 2003, 266(3): 493-514.

[14] 孫其誠, 王光謙.顆粒物質力學導論[M].北京: 科學出版社, 2009.

[15] 賈富國, 韓燕龍, 劉楊, 等.稻谷顆粒物料堆積角模擬預測方法[J].農業工程學報, 2014, 30(11): 255-256.

[16] 王瑞芳, 李占勇, 竇如彪, 等.水平轉筒內大豆顆粒隨機運動與混合特性模擬[J].農業機械學報, 2013, 44(6): 93-94.

[17] 黃志剛, 朱清萍, 朱慧, 等.轉筒干燥器內顆粒物料運動的模擬與試驗研究[J].糧油加工, 2004, 11(2): 65-66.

[18] 高紅利, 陳友川, 趙永志, 等.薄滾筒內二元濕顆粒體系混合行為的離散單元模擬研究[J].物理學報, 2011, 60(12): 3-5.

[19] 劉楊, 韓燕龍， 賈富國, 等.橢球顆粒攪拌運動及混合特性的數值模擬研究[J].物理學報, 2015, 64(11): 6-7.