大學物理中霍爾效應實驗教學的進一步研究

張秀蘭，余海軍

（淮南師范學院電子工程學院，安徽 淮南 232038）

1 前言

霍爾效應時在1879年被美國物理學家霍爾在研究金屬的導電機制時發現的，霍爾效應是電磁效應的一種[1]。隨著當時社會的半導體技術的不斷成熟與提高，出現了各種半導體霍爾元件，利用霍爾效應可以確定半導體材料的導電類型、載流子濃度及遷移率、半導體的禁帶寬度等[2]。霍爾效應在傳感器中的應用也特別重要，隨著社會科學技術的不斷發展，電子集成技術逐步走向成熟，也出現了將霍爾半導體元件和相關的信號調節電路集成在一起的霍爾傳感器[3]。霍爾效應是在物理學中重要的物理現象[4]，是作為物理專業的學生必須掌握的，對霍爾效應以及霍爾效應實驗的研究可以加深我們對霍爾效應的深入認識以及對霍爾效應的靈活運用。也可以為以后能在有關霍爾效應技術方面發展奠定基礎。

2 霍爾效應實驗原理

如圖1.1所示，我們可以將一個半導體或導體材料[5]，沿Z方向加磁場B，沿X方向加電流大小為I。

圖1 霍爾效應原理圖

3 霍爾效應實驗過程

霍爾效應實驗的主要內容是通過測定霍爾電壓來完成對霍爾系數的測量,霍爾系數是反映半導體材料霍爾效應強弱的重要參數。不過在實驗產生霍爾電壓的同時,也會隨著產生各種效應,所以實驗測量的霍爾電壓并不是真正的霍爾電壓,如在上面所說的，它包含著各種副效應所引起的附加電壓。下面對載流子濃度n、霍爾系數、霍爾靈敏度KH的測定在某以恒定磁場B下，測量幾組不同的電流和電壓值，以橫坐標為I，縱坐標為UH作圖，由公式，在理論上我們可以得到通過原點的直線，但由于有附加電壓的存在以及偶然誤差等因素，大多數情況下做出的圖形都不會通過原點，都會有截距存在。這時，我們可以在所做的直線上任意選取兩點的方法來求出斜率。根據公式就可以求得霍爾靈敏度KH，再根據霍爾靈敏度KH及公式就可以求得霍爾系數RH，最后我們再用公式，就能求得載流子的濃度n。

我們可以通過兩種方式來獲得KH的值，一種保持通過線圈的磁感應強度B的大小不變，通過測出IS和UH的大小進而測出斜率。另一種是保持IS不變，通過測出IM和UH的大小來測出斜率然后測出KH的值。其中B＝CIM，C是常數為0.40。

4 數據處理

4.1 求出霍爾系數、霍爾靈敏度等相關數據

由相關公式我們知道求得霍爾靈敏度KH的值，可以計算出出霍爾系數RH等的值，對于求KH的值我們有三種方法[6]，它們分別是：平均值法、作圖法、直線擬合法。這三，個方法各有各的好處，平均值法的實質是求平均斜率;作圖法的實質是求更精確的斜率;直線擬合法是求最佳斜率。下面我們分別用這三種方法分別求出表1和表2所應的KH的值。

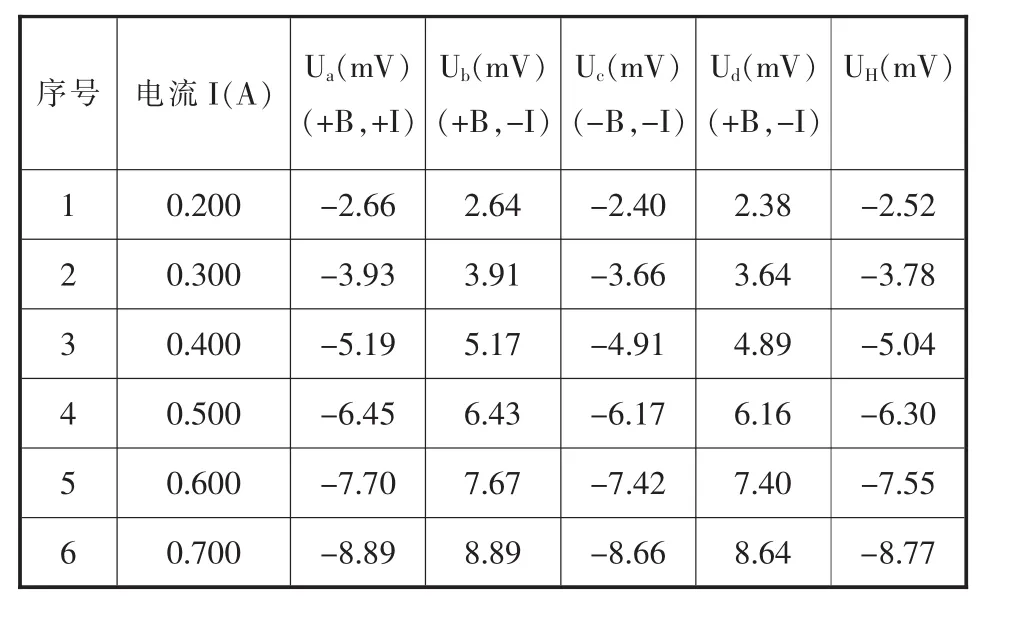
表1 保持IS不變 （取 IS=2.00mA），IM變化如下表（IM是通過線圈的電流）

表2 保持不變（取=700mA），變化如下表所示

4.2 利用霍爾效應測定螺線管軸線上的磁場分布的數據處理

因UH＝KHIB用已知KH的霍爾元件制成探頭，測出 I和 UH，可得，我們通過對獲得的數據進行分析和處理，可以得到B的大小分布圖：

圖4 單線圈B—X曲線

對于圖4。我們可以看到在在螺線管的中心位置處的磁場強度非常的強，而在逐漸遠離中心處的磁場逐漸在減弱，直至最后磁感應強度的大小趨近與零。

圖5 雙線圈B—X曲線 距離為R

由圖5我們可以看到，在兩個線圈的距離為R時，在其中心點的磁感應強度最強，如單線圈一樣，在逐漸遠離中心處的磁感應強度慢慢變弱，直至最后磁感應強度趨近于零。

圖6 雙線圈B—X曲線 距離為2R

對于圖6。我們可以看到它不同于單線圈和兩線圈的距離為R的線圈的磁感應強度在空間上的分布。在中心點處，其磁感應強度為一個極值。而在大概+100mm處和-100mm處的磁場強度最大，并在遠離+100mm和-100mm處，磁感應強度逐漸變小，直至最后趨近于零。

在對上面誤差出現的原因的分析，我們可以簡單總結如對霍爾效應的影響因素為：不在同一等勢面而引起的電勢差、溫差電勢差、由于電阻不等引起的電勢差、各載流子遷移速度不同引起的電勢差以及偶然誤差。

參考文獻：

[1]劉戰存，鄭余梅.霍爾效應的發現[J].大學物理，2007,26(11)：51-56.

[2]王本菊.霍爾效應及其應用.中國校外教育.2011,6:176-177.

[3]王化祥，張淑英.傳感器原理及應用[M].天津：天津大學出版社，1988：23-27.

[4]丁慎訓，張連芳.物理實驗教程[M].北京：清華大學出版社，2003.

[5]張海濤.霍爾效應及應用[J].溫州職業技術學院學報.2005,5(4).

[6]曲華，鄒進和，董三壯.霍爾效應實驗及數據處理[J].大學物理實驗，1998,11(4)：53-56.