試談托盤天平教學的新思路

石堯 陳曉陸 張迎杰

摘 要：針對托盤天平在初中物理教學中存在的癥結，以教育重演論為教學設計的理論基礎，采用重演托盤天平發明及改進過程中關鍵環節的教學思路，對托盤天平的教學流程進行了重構.

關鍵詞：托盤天平；教育重演；過程教學；教學思路

一、提出問題

托盤天平作為初中物理引入最早、復雜程度最高的實驗儀器，歷來都是教學的重點和難點.關顧當前“托盤天平”的教學，一般存有兩種典型的教學方式，一是教師結合多媒體中的天平構造圖，為學生闡述每個構件的名稱與作用；二是教師讓學生閱讀書本相關內容，然后就學生提出的疑惑予以解答，抑或用提問的形式幫助學生夯實天平構件的作用.然而實際教學卻表明，這兩種方式的效果均不明顯，只能導致學生對天平構件的“死記硬背”，徒增認知負荷.

概而言之，前者囿于“教師中心論”的桎梏，忽視了學生的主觀能動性，使學生只能被動地接受教師的灌輸；后者采用“教師解惑”的方式則深陷“學生中心論”的泥淖，過分夸大了學生的主觀能動性，有礙學生獲得系統的知識，致使教學失之功利；而“教師提問”的方式看似是教師在引導學生學習，但由于提問內容只能引起簡單的聯結式反應，根本無法調動學生的高階思維，因而也不可能取得預想的效果.于是如何使學生徹底理解并牢記托盤天平各構件的功能，就成為了物理實驗教學中亟待解決的要務.

歷經思忖，我們認為上述癥結的產生濫觴于教學中對物理知識來龍去脈的漠然處之，忽視了學生對知識形成過程的體驗，進而嚴重束縛了學生的思維，泯滅了其創造力，顯然與培養學生核心素養的教學目標背道而馳.

二、凸顯過程的托盤天平教學思路

（一）理論基礎

澳大利亞學者斯威勒將阻礙學生學習的認知負荷分成內部認知負荷和外部認知負荷兩類.內部認知負荷取決于學習材料與學習者專業知識之間的交互程度；外部認知負荷則由教學設計不當而引起，直接受控于教學的設計者[1].由此可見，若要降低學生的認知負荷，促成有意義學習的發生，在教學過程中就應該盡可能地使教學設計契合學生的認知規律.就本節教學而論，天平各組件的介紹不應以并行羅列的方式呈現給學生，而應遵循一定的邏輯順序，由此才能輔助學生大腦進行組織編碼，將凌亂而紛雜的構件有條理地串接起來，形成系統的認知結構.那么究竟以何種邏輯順序展開托盤天平的教學呢？這里，教育重演論為我們提供了可資鏡鑒的寶貴啟示.

教育重演論將現代學生的學習過程看作是對人類文化發展過程的一種認知意義上的重演，學習者在學習科學知識過程中所遇到的困難往往是人類在科學研究過程中需要長時間累積、消化的突破點[2].進一步將教育重演論與物理教學實際相結合，理想的物理教育便應該是以濃縮的時空和必然的形式，再現物理知識、實驗儀器在形成過程中遇到的關鍵問題，從而幫助學生突破思維障礙，汲取前人智慧.鑒于此，我們結合教育重演論的思想精髓，以天平發展歷程為縱軸主線，以追求精密測量為橫向鋪墊，對本節課的教學流程進行了重構.

（二）教學流程

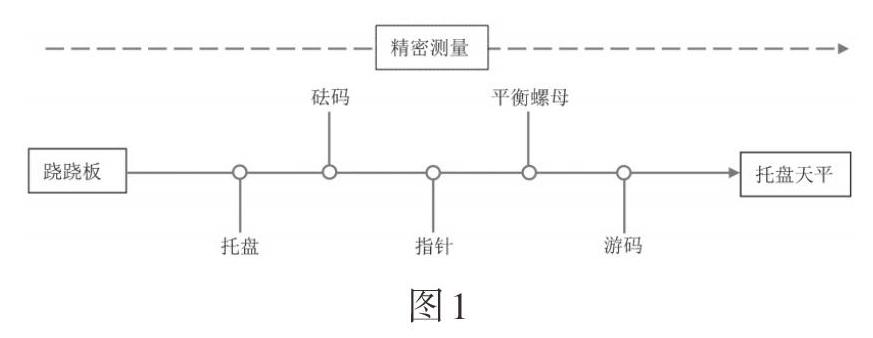
1.蹺蹺板：天平雛形

回溯世界發明史，各種發明創造或多或少都是從某種事物的性能或特性中得到啟發的原型，從而取得成功的.眾所周知，托盤天平的實質是一個等臂杠桿，因此相應教學就要以生活中常見的等臂杠桿為邏輯起點.在此，我們選擇了平時孩子們娛樂所用的蹺蹺板為構建托盤天平的原型.首先，教師著力為學生夯實蹺蹺板水平的意義，在蹺蹺板兩側距支點O相等的位置分別放置重物，質量大的一側會下沉；而當兩端物體質量相等時，則會出現蹺蹺板水平的現象，這種“相等”關系的出現可以幫助我們衡量物體質量的大小，即如果知道一側物體的質量，就可以通過“相等”的關系，得出另一側物體的質量.從而揭示蹺蹺板中蘊藏的測量功能.

2.托盤：盛裝物體

在充分明確蹺蹺板的測量功能，成功建構出托盤天平的雛形后.教師可繼續發問，將蹺蹺板作為測量物體質量的工具，將會遇到一個棘手的問題，蓋因蹺蹺板只有一根橫梁，放置其上的物體會由于重心不穩等原因而傾倒.同時由于放置位置、物體重心位置等因素的影響，亦會造成“杠桿”看似等臂，實則并非等臂的窘境.那么該如何破解這些疑難呢？繼而引導學生提出“引入托盤這種構件”來解決上述問題，這是因為“托盤”在使物體穩定放置的同時，相應承接托盤的支架還使得橫梁受力更為均勻、集中，并間接確定了兩端的力臂長短，使“蹺蹺板”成為了名副其實的等臂杠桿，由此對物體質量的測量也變得更為精密.

3.砝碼：以碼衡物

但是隨后一個新的問題又出現了，用實物質量衡量物體質量存有諸多不便，如不方便攜帶，實物質量不唯一確定等.于是為確定測量標準，可采取“替代”的方法，用較重的金屬塊替換相應實物，從而誕生出金屬制砝碼的雛形，但這種仿形砝碼沒有具體的數量值，而是代以相應的實物名稱，如雞、羊、牛等，因而難以直接量化比較與數量加成.接下來，為完成定性向定量的轉變及加深“標準”的感覺，砝碼又逐漸演變為質量元器的模樣，并參照貨幣面值的分配形式，對砝碼規格予以明確界定.最終使砝碼成為了質量量值傳遞的量具，進一步精確了天平的測量結果.

4.分度盤與指針：判斷平衡

眾所周知，能夠準確稱量的關鍵在于蹺蹺板能否水平平衡，然而由于人眼的局限，難以分辨微小的形變，因此如何更為準確地判斷蹺蹺板水平自然就成為了下一個有待解決的問題.于是教師藉此發問：有什么方法能夠幫助我們更為精確地觀測蹺蹺板是否水平平衡呢？并借機向學生介紹“轉換法”.所謂“轉換法”，是指在保證效果相同的前提下，將不易觀察的現象轉換成易于觀察的現象，將難以測量的物理量轉換為能夠測量的物理量的方法.由此帶領學生在蹺蹺板上植入指針與分度盤這套裝置，由指針的偏轉方向來表征托盤天平中物體質量的孰大孰小，而分度盤中格數的劃分則更加精密地反映出天平的傾斜程度.從而為增減砝碼提供判據.

5.平衡螺母：消除干擾

至此，托盤天平已初見端倪，接下來，天平將由設計藍圖步入實際操作，此時再次遭遇了新的疑難，即放被測物體之前，托盤質量不等及橫梁質量分布不均等問題，皆會造成天平以不平衡的初態“登場”，擾亂后續測量結果的準確性，那么該如何排除這些干擾呢？這里又涉及到一種新的科學方法，即抵消法，是指在無法徹底消除無關變量的前提下，可設法抵消無關變量產生的影響.就上述天平所遇困境而言，可在橫梁兩端懸掛配重，同時為保證配重在移動過程中能保持穩定與連續，可將配重設計為半固定的、“旋進式”的平衡螺母，并結合學生的日常生活體驗，得出平衡螺母的調節準則.

6.游碼：測微小量

確保天平在測量之前達到水平平衡后，便開始了我們的測量.在測量過程中有時會遇到“放入最小砝碼，指針偏右；取出最小砝碼，指針偏左”的情況，相關疑問亦隨之而來：如何測量比最小砝碼還小的質量呢？這時可指導學生借助剛才所學“平衡螺母”的相關知識進行原型啟發，將一定質量的金屬塊（謂之“游碼”）置于橫梁前側的標尺上，使其可自由移動，進而結合標尺數值來測算微小質量.蓋因標尺以直尺為原型，零刻線位于最左側，與游碼左側對齊，由此較好地詮釋了“左物右碼”的測量規定.需要說明的是，不同于砝碼“臂定而尋力等”的平衡物體方式，游碼得益于數理工具的進步，采用的是“力定而尋臂值”的制衡物體方式.

三、結語

縱覽托盤天平教學的整個流程，師生化身托盤天平的創造者，攜手重演天平發明及改進過程中的六個關鍵環節，以“蹺蹺板”為設計原型，依次添加“托盤”、“砝碼”、“平衡螺母”等天平在研發過程中所需的構件（如圖1所示），并借助“解決問題”的問答形式，滲透精密測量的物理觀念與精益求精的科學精神，激發學生的想象力與創造力，使其迸發智慧的火花.進一步而言，雖然文中探討的天平教學思路僅僅是整個初中物理實驗教學研究中的一小步，但其背后所蘊含的觀念卻有著深遠的意義，它為物理實驗儀器的教學開啟了一種新的方式，為其他儀器的教學設計提供了可資鏡鑒的模板.

參考文獻：

[1]石堯，邢紅軍.以科學方法為中心實施因材施教的物理教學途徑研究[J].課程·教材·教法，2016，36（3）：98-102.

[2]石堯.中學物理過程教學的實踐探索[J].中小學教師培訓，2017（7）：67-69.