滲透數學史教育之微課程開發與應用的教學研究

趙智勇

（教育教研信息中心，河南安陽 455000）

全日制義務教育《數學課程標準（修改稿）》中指出：“數學是人類文化的重要組成部分，數學素養是現代社會每一個公民應該具備的基本素養”[1]。張奠宙先生曾說過：“當數學文化的魅力真正滲入教材、到達課堂、溶入教學時，數學就會更加平易近人，數學教學就會通過文化層面讓學生進一步理解數學、喜歡數學、熱愛數學”[2]。因此，數學的教與學的過程應該成為文化的傳播與交流的過程。

隨著時代的發展和網絡的普及，教育教學方式正在悄然發生著一些變化，微課程在中學數學教學中的應用越來越受到重視，下面是在實驗學校教學班數學教學中進行的針對綜合題教學 “利用微課程滲透和傳播數學史料中所蘊含的數學思想方法”的教學實踐及思考。

1 引入史料，開發微課

1.1 問題的引入

我國古代《九章算術》勾股章中有：“今有勾五步、股十二步，問:勾中容方幾何?”[3]這個問題實質上就是：“已知直角三角形的三邊長分別為5、12、13，求該直角三角形中內接正方形的邊長。”問題包含兩種情況（見圖1）：

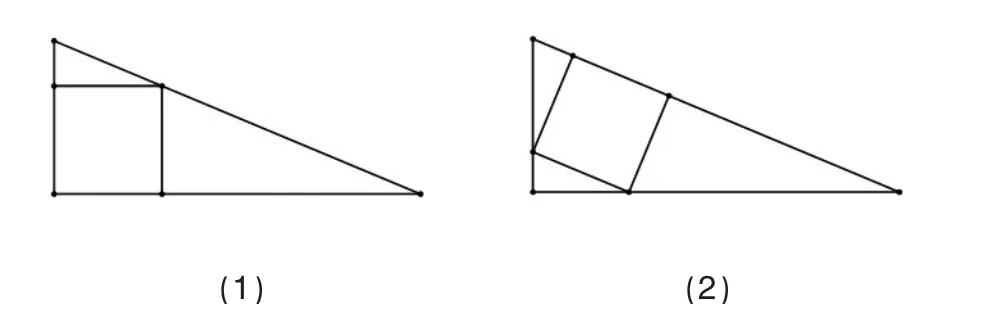
圖1

劉徽為勾股容方的關系式提供了兩個證明，一個是利用出入相補原理；另一個證明是利用相似三角形比率不變原理。

1.2 問題的延伸

這個問題在教學中是相似三角形的典型應用問題，圖1中隱含著一個特殊的、應用廣泛的相似模型——“三直角型”，以下圖2中幾種圖形等都是其基本形態或變式圖形：

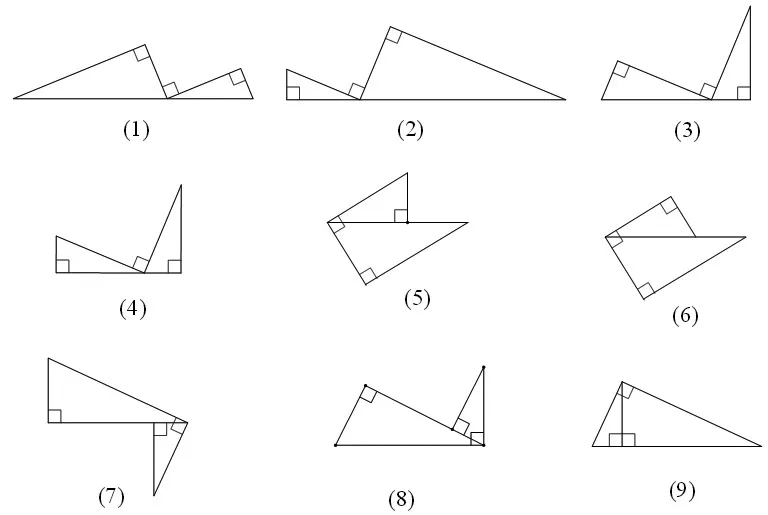
圖2

上述相似模型的本質用文字表述即為：當兩個直角三角形的非對應銳角之和為90°時，這兩個直角三角形相似。

2 引進教學，感受本質

本節課教學選題的主要對象是“河南中考2016年23題”，為了給學生解決與直角三角形有關的綜合題問題提供啟示和幫助，在實際教學中，我們首先引導學生先觀看上述微課程，并針對收獲進行了交流和適度引導。接著出示了下面的例題。

例 1：如圖 3，在平面直角坐標系中，已知 D（2，0），E（2,1），將△ODE繞點O逆時針旋轉α度得到△OD′E′，且，求點 D′、E′的坐標。

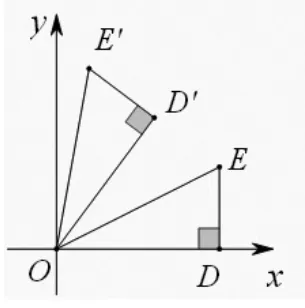
圖3

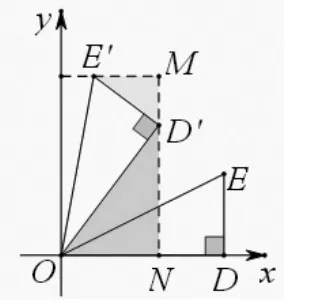
圖4

分析：在平面直角坐標系下，可利用平面直角坐標系兩條坐標軸相互垂直的特征，過旋轉后的直角頂點作平行于坐標軸的直線構造“三直角型”相似模型，列比例式解之。為此分別過點D′、E′作x軸、y軸的垂線（圖 4），利用△OND′∽△D′ME′可求得

例 2：（河南中考2016年 23題）如圖 5，直線 y=-交 x軸于點 A，交 y軸于點 C（0，4），拋物線 y=經過點 A，交 y軸于點 B（0，-2）。 點 P為拋物線上一個動點，過點P作x軸的垂線PD，過點B作BD⊥PD于點D，連接PB，設點P的橫坐標為m。

（1）求拋物線的解析式；

（2）當△BDP為等腰直角三角形時，求線段PD的長；

（3）如圖 6，將△BDP繞點 B逆時針旋轉，得到△BD′P′，且旋轉角∠PBP′=∠OAC，當點 P 的對應點 P′落在坐標軸上時，請直接寫出點P的坐標。

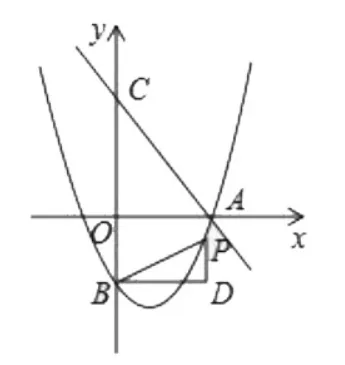
圖5

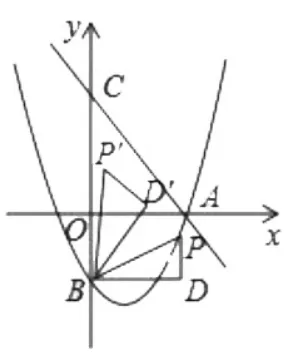
圖6

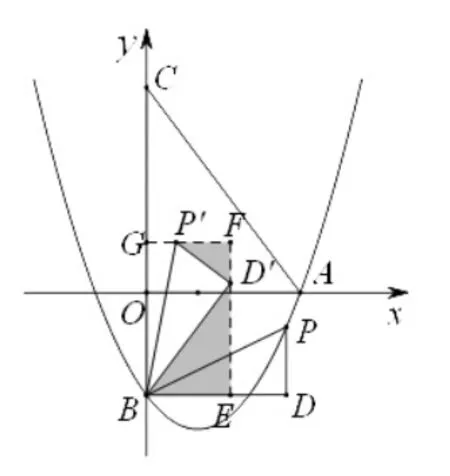
圖7

此題第（3）問作為全卷的壓軸，綜合性強，共有三種情況符合題意，具有相當的難度。如果能表示出P′點的坐標，那么點P落在坐標軸上時，分別令P′點的橫坐標和縱坐標為0，構造方程并解方程即可得到結果。

由于教學本題之前，學生觀看了前面提到的微課程并進行了交流，又有了解決例1的經驗，教學時通過啟發學生聯想微課程和例1，通過添加輔助線構造“三直角型”相似模型（如圖 7）解答第（3）問。 即設利用△BED′∽△D′FP′可得到用 m 表示的點P'的坐標分別令P'的橫坐標和縱坐標為0，解方程即可得到5的坐標。這樣順利完成了本節課重點例題——例2的教學。

3 引導反思，總結收獲

完成例題教學之后，教師和學生一起回顧本節課的教學，從數學文化、數學美和解題策略三個角度進行了教學小結，主要歸納了以下三點：

（1）品味數學史上問題的解決過程，對學習有啟發和促進的作用。

（2）平面直角坐標系中涉及直角三角形旋轉的問題，求點坐標時，可以過旋轉后的直角三角形頂點作平行于坐標軸的直線，構造“三直角型”相似模型，“將不規則圖形變為規則圖形，或將分散的條件集中在一起，以便挖掘隱含條件，使問題得以解決”[4]。

（3）“三直角型”相似模型反映的是數學客觀規律，其形態優美，應用廣泛，構造和利用“三直角型”相似模型，列含有未知數的比例式計算相關線段的長度，往往簡捷、快速。

4 承載文化，培育素養

數學承載著思想和文化，是人類文明的重要組成部分[5]。通過微課程滲透數學史教育，讓學生在觀看微課程的同時，經歷解決問題的過程，感悟數學史料中蘊含的解決問題的思路和方法，并通過具體實例加以鞏固，既滲透了數學文化，增強了學生學習數學的興趣，又有利于提高探究能力。課后的調查問卷顯示78.1%的學生認為引入數學史的微課程對數學學習很有幫助，20.5%的學生認為對數學學習比較有幫助；幾乎所有的學生都希望老師在教學中使用數學史內容，其中期望課堂上講授數學家故事、數學游戲、經典數學名題、數學知識的發展歷史的學生分別占63%、68.5%、48.2%、64.4%。

5 結語

總之，利用微課程給學生滲透數學文化，揭示數學史料中所蘊含的數學思想方法，能夠促進數學文化更有效的傳播，使得數學文化的滲透更加靈活，有利于拓展學生的視野，進而改變學生的數學觀、數學情感，激發學習興趣，培育學生的數學素養，進一步提高教學效果。

參考文獻

[1]中華人民共和國教育部.義務教育數學課程標準[M].北京：北京師范大學出版社，2011.

[2]吳賽瑛.例談數學教學設計的若干關鍵點[J].福建中學數學，2011（3）：21-24.

[3]曾海龍，譯解.九章算術[M].南京：江蘇人民出版社2011.

[4]王曉軍，汪曉勤.HPM視角下“圖形旋轉”問題探究[J].數學通報，2012（5）：16-19.

[5]中華人民共和國教育部.普通高中數學課程標準[M].北京：人民教育出版社，2018.