擬合復雜形狀主骨架的顏色漸變填充

王家潤，任 菲，榮 明，羅童心

(1.華北計算技術研究所 基礎三部，北京 100083； 2. 國防大學 信息作戰與指揮訓練教研部，北京 100091)

0 引言

人類的視覺大部分來自于形狀及顏色等視覺感知因素[1]。在軍事作戰符號體系中，不同國家對作戰符號顏色的使用等都有明確的規定[2-3]，作戰符號顏色的漸變填充具有重要的視覺增強作用：增強與背景的對比度，更加突出顯示作戰符號；增強進攻類作戰符號等的作戰方向意圖的視覺表現等。

在二維圖形QT(一種跨平臺C++圖形用戶界面軟件)或圖形設備接口(Graphics Device Interface, GDI+)中，一般提供常用的中心徑向漸變、線性漸變等顏色漸變填充效果，但在三維圖形中沒有該類算法(一般采用掃描線種子填充算法等)，而且針對比較復雜的形狀，這些填充算法無法較好地實現沿形狀的主要延伸方向的顏色漸變填充效果。骨架(或中軸)能較好地表達形狀(或區域)的整體延伸趨勢，描述形狀的主要幾何特征，反映形狀的整體拓撲結構[4]；因此，針對復雜形狀的研究，通過其骨架可得到較大的簡化。文獻[5]對骨架提取進行了比較全面的論述；文獻[6]對在地理信息系統(Geographic Information System, GIS)中基于約束Delaunay三角剖分(Constrained Delaunay Triangulation, CDT)提取骨架進行了比較研究；文獻[7]對圖像處理中的骨架提取算法進行了分類并比較了優缺點。骨架提取算法中存在的共性問題是骨架對輪廓細節過于敏感，從而產生很多的細小分枝[8-10]，這些細小分枝的存在給實際應用帶來較大的困難，因此，冗余分枝的裁剪成為骨架提取研究中的難點。文獻[11]采取符合視覺特性的彎曲度比率(Bending Potential Ratio, BPR)抑制分枝，大部分的骨架提取算法采用的策略與之類似：在提取的過程中對骨架分枝按照一定的規則進行裁剪。本文的主要工作有：

1)基于骨架路徑評價向量的骨架冗余分枝裁剪。

基于視覺顯著性評價向量，優選出少量的骨架路徑，較好地抑制了骨架的冗余分枝。這種基于骨架路徑的整體選優策略，與常用的基于骨架分枝進行局部裁剪的方法不同。

2)基于形狀主骨架的顏色漸變填充。

對主骨架進行顏色漸變計算，并將顏色計算拓展到整個形狀區域，實現了沿形狀延伸變化的漸變填充。而常用的中心徑向、線性漸變等填充樣式，一般較難實現該種效果。

1 形狀主骨架優化及顏色漸變填充算法

1.1 算法整體流程

約束條件：限定形狀(或區域)為無洞的簡單多邊形[4]；形狀的邊界點依次相連構成封閉多邊形。

1) 輸入形狀的邊界點集合；顏色漸變開始與結束顏色。

2)過程如下：

①分解復雜區域為較簡單區域；

②對各區域進行約束Delaunay三角剖分；

③對三角形進行分類，采用三角形中線法提取骨架構建骨架二叉樹；

④采用路徑棧及搜索棧，提取骨架路徑集合；

⑤依據視覺顯著性評價向量，對骨架路徑進行評價；

⑥依據評價結果，優選出主骨架；

⑦對主骨架進行幾何調整優化；

⑧對主骨架進行顏色漸變插值計算；

⑨依據主骨架，將區域邊界點分類，采用分組計算及點到線段的投影插值進行漸變顏色拓展映射計算；

⑩將各區域進行整體合成。

3)輸出與形狀的邊界點集合對應的顏色集合。

1.2 算法詳細解析

1.2.1 CDT三角形中線法骨架提取

1)約束Delaunay三角剖分。

針對復雜形狀，可采用區域分解策略分解為比較簡單的形狀[4]。在三維中的簡單多邊形，如果存在凹點則不能進行正確的渲染，需要進行凸分解。三角形是最簡單的凸多邊形，而且在三維圖形中渲染時，三角形是最基本的處理單元，顯卡也對三角形處理有一定的優化。約束Delaunay三角剖分較好地解決了凹多邊形的凸分解問題，在計算機圖形中有廣泛的應用，相關理論及算法也比較成熟[4,12]，而且Delaunay三角形的最小角最大特性使剖分產生的三角形避免了狹長三角形，趨向等邊三角形，較大程度上保證了剖分的趨向均勻性，可使提取出的骨架抖動性較小，更好地逼近理想的骨架。

2)CDT三角形中線法骨架提取。

CDT產生的三角形分為三種類型：Ⅰ類型，只有一條邊與其他三角形相鄰(虛線表示該邊與其他三角形相鄰)，如圖1(a)；Ⅱ類型，只有兩條邊與其他三角形相鄰，如圖1(b)；Ⅲ類型，每條邊都與其他三角形相鄰，如圖1(c)。基于上述分類，采用三角形中線(或重心)法提取三角形的骨架，參見圖1中三類三角形內部各骨架線段，其中Ⅲ類型內部含三段骨架線段。

從圖2中內部較粗的骨架線可看出，骨架的端點是Ⅰ類三角形的邊界頂點；骨架的連接點是Ⅱ類三角形非邊界的內部邊中點；骨架的分枝點是Ⅲ類三角形的重心。由文獻[12]可知，該方法提取的骨架不是嚴格意義上的骨架(或中軸)，只是近似骨架，但與三角形外心法骨架提取方法相比，該方法可保證骨架點在三角形內部。使用角平分線方法[4]提取的骨架，一般在每一個凸點產生一個細小骨架分枝，圖2中至少會有8個細小骨架分枝，而CDT三角形中線法提取的骨架分枝則僅有3個，這說明CDT對骨架冗余分枝具有一定的裁剪能力。總體來看，CDT三角形中線法骨架提取方法具有計算簡單、冗余骨架分枝較少、逼近理論骨架等優點。

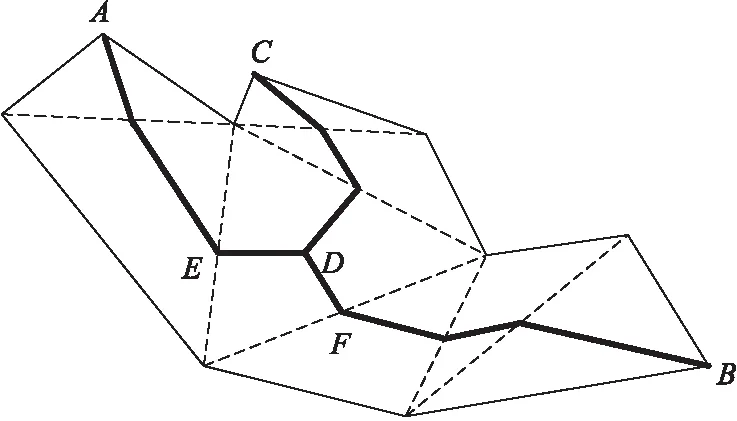
圖2 CDT三角形中線法提取骨架的示意圖 Fig. 2 Skeleton extraction by CDT triangular midline

1.2.2 骨架二叉樹構建及遍歷

從CDT三角形中線法可看出，骨架在Ⅰ、Ⅱ類三角形內部以一線段(該線段稱為骨架線段，線段的端點稱為骨架點)表示，在Ⅲ類三角形內部由3個線段組成。下面采用骨架節點對骨架線段進行邏輯表達，骨架節點與骨架點、骨架線段、所在的三角形及出入邊等有關，整個骨架在邏輯上可組織為二叉樹。

1)骨架節點數據結構。

SkeletonNode

{

/*骨架節點所在的約束三角形索引，用于建立骨架節點與約束三角形的關聯*/

unsigned int triIndex;

/*骨架節點的2個端點在骨架點集中的索引，用于建立骨架節點與骨架點集的聯系*/

unsigned int skIndex1;

unsigned int skIndex2;

/*骨架線段方向標志：當所在的三角形為Ⅰ類型，從頂點到對邊置為1，否則為-1；當所在的三角形為Ⅲ類型，從中心點到對邊置為-1，否則為1*/

int flag;

/*當所在的三角形為Ⅱ類型，用ed1記錄入邊信息，ed2記錄出邊信息；當所在的三角形為Ⅰ、Ⅲ類型時，只使用ed1，用于建立骨架節點與所在的三角形邊的聯系*/

Edge ed1;

Edge ed2;

//父子節點指針

SkeletonNode* pParent;

SkeletonNode* pLeft;

SkeletonNode* pRight;

//是否訪問標志

bool visited;

}

2)骨架二叉樹的構建。

a) //設置隊列qe，用于廣度優先遍歷

std:: queue< SkeletonNode *> qe.

b) /*從CDT三角形集合中查找一個Ⅰ類三角形，取骨架線段，建立骨架節點pRoot，作為骨架二叉樹根節點，并將該骨架根節點入隊列qe*/

pRoot =createRootNode(CDT三角形集合);

qe.push(pRoot).

c) while(qe非空)

{

//獲取隊列前端節點指針

SkeletonNode* pCurNode = qe.front();

//隊列前端節點出隊列

qe.pop();

/*從節點pCurNode出發，依骨架走向，檢查相鄰的三角形：Ⅰ、Ⅱ類型生成1個骨架節點；Ⅲ類型生成3個骨節點，依據骨架生成走向將入段設為父節點，其余2段設為子節點。建立與節點pCurNode的父子關系，并將生成的節點加入到隊列qe中*/

pushSkeletonNode(pCurNode, qe).

}

3)骨架二叉樹的遍歷。

a) //設置棧sk，用于深度優先遍歷

std::stack sk.

b)//將骨架二叉樹根節點入棧

sk.push(pRoot);

c)while(sk非空)

{

//獲取棧頂節點指針

SkeletonNode* pCurNode = sk.top();

//棧頂節點出棧

sk.pop();

//右子節點入棧

sk.push(pCurNode->pRight);

//左子節點入棧

sk.push(pCurNode->pLeft);

//訪問節點pCurNode中的信息

//pCurNode->visited…

}

1.2.3 骨架路徑雙棧跟蹤提取

骨架路徑[10]可采用骨架節點隊列、骨架點列等表示。從骨架二叉樹中根節點的選擇可看出，根節點只有1個孩子節點，從幾何的角度來看骨架的各分枝端點，骨架根節點與葉子節點是相同的，因此提取骨架路徑時把根節點與葉子節點等同處理。

1)骨架路徑提取。

兩節點之間的骨架路徑雙棧跟蹤提取過程如下。

a) std::vector< SkeletonNode*> path，保存輸出的骨架徑上的節點；std::stack ps(用于跟蹤骨架路徑，簡稱路徑棧)；std::stack ss(用于放置搜索節點，簡稱搜索棧)。

b) 骨架路徑的雙棧跟蹤提取基本流程，如圖3所示。

c) 補充說明。

對節點pNext進行雙棧出入操作：

對pNext設置已訪問標志；將pNext入路徑棧ps；將pNext未訪問過的所有相鄰節點加入到搜索棧ss。

雙棧相鄰檢查：

檢查路徑棧ps棧頂節點與搜索棧ss棧頂節點是否相鄰，如果非相鄰，將ps棧頂節點出棧，直至ps棧頂節點與ss棧頂節點相鄰為止。

雙棧過濾處理：

如果ps非空，檢查ps棧頂節點pTmp；ps出棧；ps非空，檢查ps棧頂pPre，檢查ss的棧頂pSS，如果pPre不是pTmp的子節點且pSS不是pTmp的子節點，將pTmp重新入棧ps。該處理主要是消除骨架分枝點的干擾，因為在Ⅲ類三角形中，有三段骨架線段，因此需要沿骨架路徑的走向，過濾掉不符合走向的骨架線段。

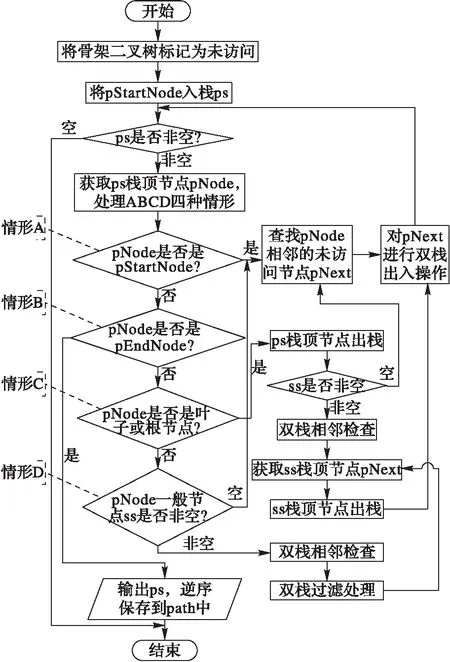
圖3 骨架路徑的雙棧跟蹤提取流程 Fig. 3 Flow chat of extracting skeleton path by double stacks

2)骨架路徑表達方式轉換。

在1)中獲取的是采用骨架節點表示的骨架路徑，在骨架繪制等應用中也采用骨架點列的表示方式。從骨架路徑中的開始節點開始，按骨架節點中的骨架線段的走向及骨架端點信息，跟蹤出每一骨架線段的骨架端點索引，因為每一相鄰骨架點重復兩次，故最后需要把中間的重復點索引刪除，即得到骨架路徑的骨架點列表示。

1.2.4 骨架路徑評價向量

已有的輪廓曲線演化骨架提取算法[13]中對邊界的輪廓點給出評價，度量該點對形狀的貢獻度，依據貢獻度簡化輪廓。借鑒上述思想，針對骨架路徑也引入評價標準，主要選用骨架路徑面積(A)、骨架路徑長度[10](L)、骨架路徑跨度(S) 3個指標，組成骨架路徑評價向量M=(A,L,S)。

骨架路徑面積：骨架路徑中各節點所在的三角形的面積之和。特別注意，如果是該骨架節點所在的三角形是Ⅲ類型，則計算該骨架節點所在的三角形重心與關聯的邊構成的小三角形的面積。

骨架路徑跨度：骨架路徑首尾兩個端點間的歐氏距離。

設計思想如下。

已有的視覺顯著性認知研究[14]認為：區域尺寸、突出等，是區域形狀顯著性的重要特征。骨架面積測量了該骨架路徑在視覺上占據的視覺范圍；骨架長度刻畫了形狀的總體延伸變化；骨架跨度度量了形狀的某延伸方向的伸展程度，該思想來源于凸殼直徑概念。總體來看，這3個幾何測量指標一定程度上可對骨架路徑進行較好的整體性評價。

計算骨架的所有骨架路徑，計算出最大長度、最大面積、最大跨度，對每條骨架路徑的3個測量指標進行歸一化處理，可使得骨架路徑評價向量具有平移、縮放、旋轉等不變性。

1.2.5 主骨架的優選及幾何優化

本文主骨架是指從骨架路徑集合中篩選出的較優的骨架路徑，與傳統的已裁剪掉細小分枝的主骨架不同。

1)視覺顯著度及主骨架優選。

從骨架路徑的構建可知，骨架路徑的首尾兩個端點也是形狀的邊界點，因此可通過對骨架路徑評價向量評價形狀的邊界點，引入視覺顯著度來測量形狀上各邊界點的視覺顯著性。形狀上各邊界點的骨架視覺顯著度初始設為0，將最長骨架路徑兩個端點對應的邊界點的視覺顯著度增加1；將最大跨度的骨架路徑兩個端點對應的邊界點的視覺顯著度增加1；將最大面積的骨架路徑兩個端點對應的邊界點的視覺顯著度增加1，形狀的各邊界點視覺顯著度≥0。

通過引入邊界點的視覺顯著度，能較好地篩選出較優的骨架路徑，輔助用戶更好地選擇出理想的骨架路徑。一般來說，主骨架基本可從視覺顯著度比較高的形狀邊界點篩選出，而這種較優的視覺顯著點相對是比較少的。

2)主骨架的幾何優化方法。

從骨架路徑篩選出的主骨架，從幾何的角度來看，主骨架應該是形狀的“對稱軸”，一般針對主骨架需要進一步進行幾何調整優化，才能實現視覺上更好的對稱。具體有3種幾何優化方式。

a)端點刪除：一般主骨架端點附近骨架細小分枝變化較大，通過端點刪除可消除這類細小分枝，提取出的主骨架能更好地能反映形狀的主要幾何變化趨勢。在選擇刪除的端點時，可參考格式塔理論中的對稱性原則[1]成對地進行選擇。

b)端點中移：將骨架端點進行調整，如圖4中的A調整到鄰邊的中點A1、B調整到B1，從幾何的角度來看，更符合主骨架的“對稱軸”幾何特點。

c)中間彎曲消除：在主骨架的分枝點附近通常會有一個抖動，如圖4中的D點，將D點消除，即將骨架線段ED、DF兩段采用新的線段EF替換，在幾何上會更光順。

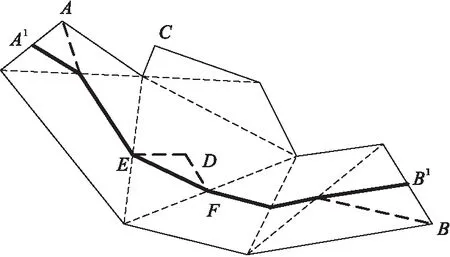
圖4 主骨架的幾何優化處理示意圖 Fig. 4 Main skeleton geometric optimization processing

通過對主骨架的幾何優化，消除了骨架的細小分枝干擾等，主骨架更加簡潔，也更加符合人類的視覺感知，可更好地服務于主骨架的顏色漸變插值計算。

1.2.6 主骨架的顏色漸變插值計算

設置顏色BeginColor、EndColor，對應主骨架的首末端點，顏色采用四維向量(R，G，B，A)描述，分量取值范圍[0,1]，A是透明度。

1) 計算出主骨架的全長skL；

2) 計算主骨架上各骨架點的顏色：

沿主骨架開始點到當前骨架點的累加長度skSum；主骨架上各點的顏色：

Color=BeginColor+(EndColor-BeginColor)*

skSum/skL

即對主骨架上各點的顏色進行線性插值。

1.2.7 主骨架到形狀邊界的顏色映射

借鑒文獻[15]中的雙緩沖區、文獻[16]中的邊界向量及形態學細化算法[9]處理的思想，設計形狀內部的主骨架到形狀邊界的整體區域的顏色填充。基本思想：將形狀的邊界點分為兩類：與主骨架直接關聯和非直接關聯。對直接關聯采用按關聯分組計算平均顏色的計算方法，對非直接關聯采用逐步由內層向外層拓展的顏色計算方法；因此，將主骨架到形狀邊界的顏色映射過程也對應劃分為Ⅰ、Ⅱ兩個階段。

主骨架到形狀邊界的顏色映射過程如下。

1)輸入形狀的邊界點集B；主骨架上各點顏色集C(依據1.2.6節，預先計算完成)。

2)主骨架到形狀邊界的顏色映射基本流程(包含第Ⅰ、Ⅱ兩個階段)，如圖5所示。

3)補充說明。

構建邊界點pt關聯的約束骨架點集S：

在CDT分解的三角形集合中，搜索邊界點pt所在的三角形的邊，構建pt關聯的約束邊集；在主骨架點集中，篩選出落在pt關聯的約束邊集上的主骨架點，構建pt關聯的約束骨架點集S。

設置點pt的顏色ptColor為主骨架路徑端點的顏色：

取主骨架端點的顏色，并以該顏色作為C中與pt對應的邊界點的顏色ptColor。

使用S計算點pt的顏色ptColor：

計算S中各點對應的主骨架上的各點顏色的平均值，作為pt的顏色ptColor。

構建index關聯的三角形集合T：

收集index對應點所在的CDT分解三角形，構建三角形集合T。

三角形tri中index點的顏色計算可行性判斷：

三角形tri中除index外的另外兩個頂點的顏色已全部計算過，且index對應點的顏色計算還未完成，則返回True，可進行顏色計算，否則，返回False。

特別注意：三角形tri中另兩個頂點顏色還沒有完成計算時，則無法計算index點的顏色，暫時先出隊列，重新追加到隊列Q的尾端，延遲這兩個頂點的顏色計算完成后再進行計算。上述處理保證了從形狀內層往外層逐步擴展顏色計算，主要是解決非主骨架的骨架分枝上的各邊界點的顏色計算。

插值計算三角形tri中index點的顏色：

在三角形tri中index點的顏色計算已可行的前提下，則可直接使用三角形tri中另兩個頂點的顏色，通過插值計算index點的顏色ptColor。具體過程：計算該點到這兩個點組成線段的最近點，如果最近點是這兩個點中的某一個，直接取該點的顏色為ptColor，如果不是端點，則將該點投影到該線段上，在該線段上進行顏色插值，計算出該投影點的顏色ptColor。

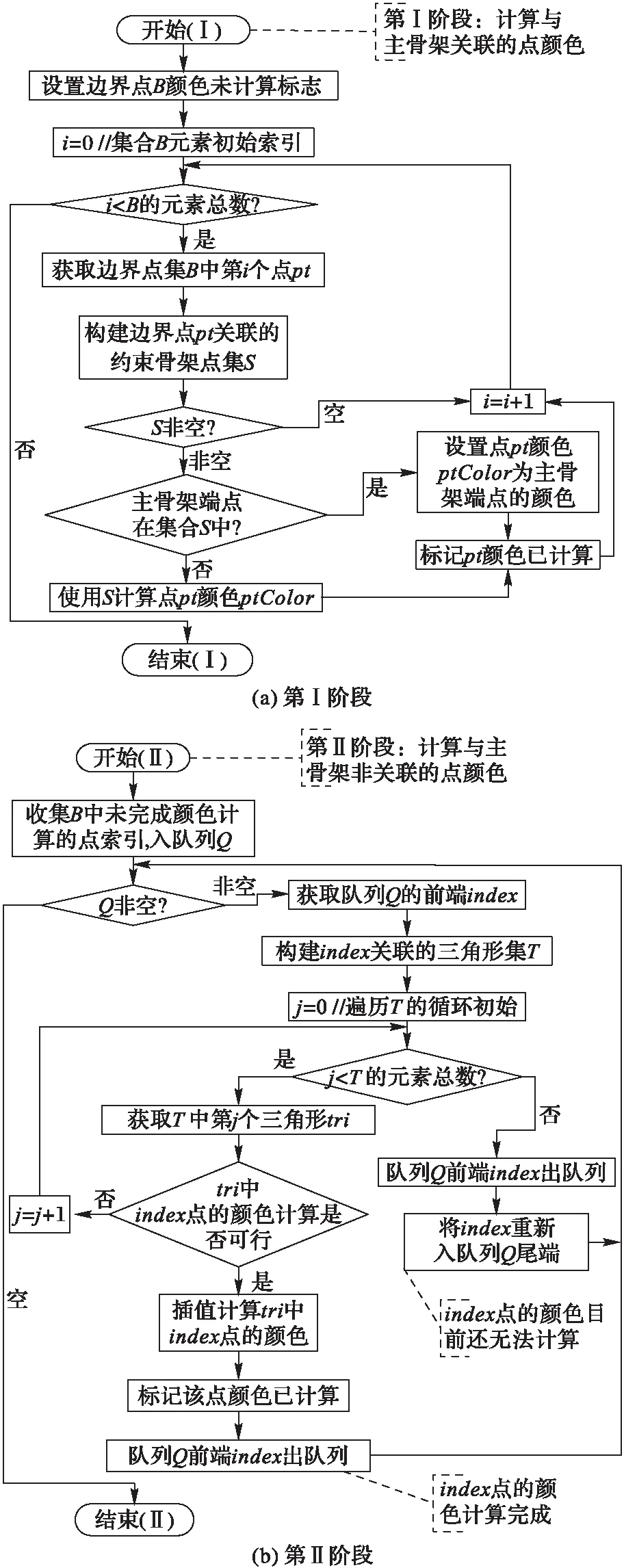
圖5 主骨架到形狀邊界的顏色映射流程 Fig. 5 Color computing from main skeleton to boundary

2 實驗及分析

2.1 實驗環境

顯卡：NVIDIA GeForce GTX 650 Ti；處理器：Intel Core 2 Quad CPU Q9500，2.83 GHz，內存3.00 GB； 三維圖形引擎OSG[17]3.0.1；Visual Studio 2010 C++。

2.2 結果及分析

參考文獻[2]中的部分軍事作戰符號，構建一般封閉多邊形、單箭頭、雙箭頭、集結地域等圖形作為實驗對象。其中，針對雙箭頭進行了形狀分解，利用左右兩部分幾何上的對稱性，在底部中間進行分割，最后對雙箭頭左右兩部分進行合成。

2.2.1 骨架提取及骨架路徑評價

1)基于CDT的三角形中線法提取骨架。

采用基于CDT的三角形中線法提取的各圖形骨架，如圖6中的各圖形內部黑色粗線所示。

在表1中，角平分線法按邊界凸點數目統計骨架分枝，該方法提取的骨架分枝數目可代表理論骨架分枝的數目，帶*數字表示真實數值不小于此處值，例如單箭頭中部的彎曲部分還存在凸點等。通過表1中骨架分枝數目對比可看出，CDT三角形中線法對骨架細小分枝具有一定的裁剪能力。

圖6 骨架提取及視覺顯著性顯示效果 Fig. 6 Skeleton extraction and visual saliency display effects 表1 不同骨架提取算法骨架分枝數目對照 Tab. 1 Skeleton branch number of different skeleton extraction methods

形狀名稱角平分線法CDT三角形中線法(相對比值)一般多邊形83(37.5%)單箭頭5*3(60.0%)雙箭頭(左、右)6*4(66.6%)集結區域11*11(100.0%)

基本結論：提取的骨架基本符合圖形的幾何中軸；骨架提取完整，驗證了三角形中線法骨架提取算法的正確性。CDT三角形中線法具有一定的骨架冗余分枝裁剪能力。

2)骨架路徑評價及優選比。

表2 骨架路徑優選前后數目統計表Tab. 2 Total number and ratio of optimized skeleton path

基本結論：通過對骨架路徑的面積、長度、跨度等的評價，優選出的骨架路徑基本符合人們對主骨架的選擇；較好地消除了大部分的骨架冗余分枝；集結區域圖形的優選比已達5.5%，優選出的骨架路徑數目有非常明顯的減少。實驗結果驗證了骨架路徑評價向量設計的合理性。

2.2.2 主骨架幾何優化及顏色漸變插值計算

從優選出的骨架路徑中，用戶可非常方便地選出主骨架。從圖6可看出，骨架端點附近及骨架分枝點附近，骨架抖動比較大，為進行顏色漸變填充，可進一步簡化，進行一定的幾何調整，該階段可通過人機交互界面進行輔助處理。對比圖6與圖7中的各對應圖形，可看出幾何優化前后的較大差異。具體采用的幾何優化措施如下：

在一般多邊形(對比圖6(a)、圖7(a))中，對主骨架的兩個端點進行了端點中移，中間的骨架分枝點處進行了中間彎曲消除；在單箭頭(對比圖6(b)、圖7(b))中，在箭頭部分的兩個骨架端點進行了端點刪除，刪除了端點附近的細小骨架分枝，對箭頭尾部的骨架端點進行了端點中移；在雙箭頭(左)(對比圖6(c)、圖7(c))，對箭頭部分的兩個骨架端點進行了端點刪除，對箭頭尾部的骨架端點進行了端點中移；在雙箭頭(右)(對比圖6(d)、圖7(d))，對箭頭部分的兩個骨架端點進行了端點刪除，對箭頭尾部的骨架端點進行了端點中移，其中頭部增加了一個非視覺顯著點的刪除，尾部沒有選擇最優的較大球端點，而是選擇了一個較小球端點，這樣可保證尾部的顏色計算與雙箭頭(左)的尾部一致；在集結地域(對比圖6(e)、圖7(e))中，選擇了接近較長路徑的端點，明顯可看出原有較多的非顯著骨架路徑端點已被過濾掉。

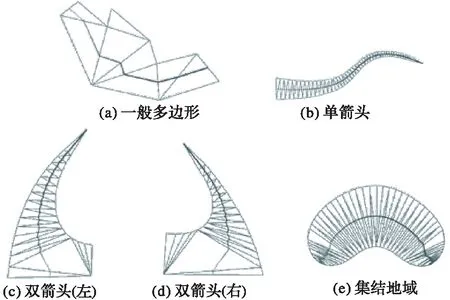
圖7 主骨架幾何優化及顏色漸變效果 Fig. 7 Main skeleton geometric optimization and color gradient filling

基本結論：通過比較幾何優化前后效果，可看出這幾種幾何調整方式的合理性：經過幾何優化后，消除了較多的細小骨架分枝，幾何對稱性較好，主骨架更加簡潔、對稱、美觀，符合對稱性美學原則，也滿足格式塔理論中的對稱性原則[1]，更加符合人類視覺感知，基本擬合形狀的主要延伸變化趨勢。

2.2.3 形狀整體的顏色漸變填充

1)單顏色透明度漸變填充。

采用紅色且只對透明度變化(雙顏色漸變處理過程相同)，參見圖8效果。

圖8 單顏色的形狀顏色透明度漸變效果 Fig. 8 Single color gradient filling effect

2)漸變填充樣式效果比較。

基于主骨架的漸變填充與線性漸變填充比較，參見圖9中虛線范圍部分。圖9(a)采用了基于主骨架的漸變填充，箭頭部分漸變自然，而且兩個箭頭頭部的顏色保證了一致性，滿足了實際應用中箭頭部分顏色要求一致的需求；而圖9(b)中使用了從上到下的顏色線性漸變，兩個箭頭顏色無法保證，線性漸變填充在表達這種效果時比較困難。圖9(c)采用主骨架線性漸變，顏色變化沿主骨架走向變化，比較自然，符合人類的視覺感知；而圖9(d)中的顏色從右到左線性漸變，尾部的透明度變化沒有沿箭頭彎曲方向。從整體來看，圖9(c)的漸變填充效果比圖9(d)的效果更好。

圖9 兩種顏色漸變填充方法對比 Fig. 9 Comparison of main skeleton and linear color gradient filling methods

基本結論：基于主骨架的顏色漸變填充能擬合形狀的延伸走勢，驗證了形狀的顏色漸變計算的合理性。與線性漸變填充相比，基于主骨架的顏色漸變填充對彎曲的條帶類等復雜區域的漸變填充效果更自然，但處理過程相對比較復雜，尤其是主骨架的選擇及幾何調整環節，需要較多的人機交互參與處理。在實際使用中，使用者可根據實際情況選擇適配的顏色漸變填充算法：形狀接近圓或矩形等，可采用中心徑向、線性漸變等顏色漸變填充；彎曲條帶類等復雜區域，宜采用基于主骨架的顏色漸變填充算法。

3 結語

本文基于CDT三角形中線法提取骨架，較好地裁剪了部分骨架冗余分枝；采用雙棧跟蹤技術提取出了骨架的全部路徑，基于提取的骨架路徑評價向量，對骨架路徑評價優選，較好地抑制了骨架的冗余分枝，給骨架提取算法中冗余分枝裁剪這一共性難點的研究提供了一種新的思路；通過引入視覺顯著性，對主骨架進行符合視覺感知的幾何優化調整，并由主骨架的顏色漸變逐步外拓到整個區域的顏色映射，實現了一種基于主骨架的顏色漸變填充新樣式，具有較好的沿形狀延伸方向的顏色漸變填充效果。實驗結果也進一步驗證了本文方法的有效性，但是基于主骨架的顏色漸變填充，處理過程相對復雜，應用條件也有一定的局限，下一階段將主要研究：1)主骨架幾何優化調整的自動化處理，減少了人機交互，進一步降低了復雜性；2)帶孔洞等復雜區域的顏色漸變填充，需將骨架的二叉樹拓展為更加通用的圖，以便進一步拓展適用范圍。

參考文獻(References)

[1] 陳為,沈則潛,陶煜波.數據可視化[M].北京:電子工業出版社,2014: 47-81. (CHEN W, SHEN Z Q, TAO Y B. Data Visualization [M]. Beijing: Publishing House of Electronics Industry, 2014:47-81.)

[2] 王飛,吳官祥,閔連權,等.軍用地圖與軍事要圖[M].北京:解放軍出版社,2013:213-215.(WANG F, WU G X, MIN L Q, et al. Military Map and Military Plotting [M]. Beijing: Chinese Peoples Liberation Army Publishing House, 2013: 213-215.)

[3] ESRI. Military analyst and Military OverLay Editor (MOLE)[EB/OL].[2017- 07- 03]. http://www.esri.com/industries/defense.

[4] 周培德.計算幾何——算法設計與分析[M].北京:清華大學出版社,2005: 43-206.(ZHOU P D. Computational Geometry—the Design and Analysis of Computer Algorithms [M]. Beijing: Tsinghua University Press, 2005:43-206.)

[5] 廖志武.2-D骨架提取算法研究進展[J].四川師范大學學報(自然科學版),2009,32(5):676-688.(LIAO Z W. A survey of 2-D skeletonization algorithm [J]. Journal of Sichuan Normal University (Natural Science), 2009, 32(5): 676-688.)

[6] 邵春麗.GIS中多邊形中軸問題和算法研究[D].武漢:武漢大學,2004:12-39.(SHAO C L. Problems of medial axis of a simple polygon in GIS and its algorithm [D]. Wuhan: Wuhan University, 2004: 12-39.)

[7] 刁智華,吳貝貝,毋媛媛,等.基于圖像處理的骨架提取算法的應用研究[J].計算機科學,2016,43(6A): 232-235.(DIAO Z H, WU B B, WU Y Y, et al. Application research of skeleton extraction algorithm based on image processing[J]. Computer Science, 2016, 43(6A): 232-235.)

[8] 孫德超,辛士慶,周亞訓,等.重要性驅動的中軸線[J].計算機輔助設計與圖形學學報,2016,28(12):2107-2113.(SUN D C, XIN S Q, ZHOU Y X, et al. Importance driven medial axis [J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(12): 2107-2113.)

[9] 王婉心,賈立鋒.骨架提取中的毛刺去除方法[J].廣東工業大學學報,2014,31(4):90-94.(WANG W X, JIA L F. The method of removing burrs in skeleton extraction [J]. Journal of Guangdong University of Technology, 2014, 31(4): 90-94.)

[10] 鄭加寬.基于骨架特征的形狀識別方法研究[D].南昌:南昌航空大學,2014:1-44.(ZHENG J K. Research on shape recognition method based on skeleton features [D]. Nangchang: Nanchang Hangkong University, 2014:1-44.)

[11] 周丹鳳.視覺顯著性特征約束下的形狀骨架提取與分解研究[D].合肥:合肥工業大學,2013:10-45.(ZHOU D F. Shape skeleton extraction and shape decomposition based on visual saliency features [D]. Hefei: Hefei University of Technology, 2013:10-45.)

[12] 王曉燕,羅靜,郭光毅,等.一種構建復雜平面圖形中軸的方法[J].地理空間信息,2015, 13(4):120-122.(WANG X Y, LUO J, GUO G Y, et al. Constructing method for approximate medial axis of planar free-form shape [J]. Geospatial Information, 2015, 13(4): 120-122.)

[13] 高立青,王延章.基于截線法的快速骨架提取算法[J].自動化學報, 2016, 42(7): 1100-1112.(GAO L Q, WANG Y Z. A fast algorithm of skeleton extraction based on secant line method [J]. Acta Automatica Sinica, 2016, 42(7): 1100-1112.)

[14] 劉雨.基于邊界特征點提取的網格分割[D].長春:吉林大學,2016:1-31.(LIU Y. Mesh segmentation via boundary feature points extraction [D]. Changchun: Jilin University, 2016: 1-31.)

[15] 劉小鳳,吳艷蘭,胡海.面狀要素的多層次骨架線提取[J].測繪學報,2013,42(4):588-594.(LIU X F, WU Y L, HU H. A method of extraction multiscale skeletons for polygonal shapes [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 588-594.)

[16] 胡斯淼,任洪娥,于鳴,等.基于向量內積的新型骨架提取方法[J].液晶與顯示,2015,30(5):844-850.(HU S M, REN H E, YU M, et al. A new skeleton extraction method based on vector inner production [J]. Chinese Journal of Liquid Crystals and Displays, 2015, 30(5): 844-850.)

[17] OpenSceneGraph (OSG) [EB/OL]. [2017- 07- 03]. http://www.openscenegraph.com.

This work is partially supported by the National Natural Science Foundation of China (61703412), the China Postdoctoral Science Foundation (2016M602996).

WANGJiarun, born in 1968, M. S., senior engineer. His research interests include virtual reality, high performance computing, data visualization.

RENFei, born in 1985, M. S., engineer. Her research interests include virtual reality, data visualization.

RONGMing, born in 1978, Ph. D., lecturer. His research interests include war simulation, strategic war game, weapons and equipment system simulation.

LUOTongxin, born in 1994, M. S. candidate. Her research interests include virtual reality, data visualization.