歐拉角姿態解算的改進
野瑩瑩,張艷珠,鄒心宇,陳 蕾,左 越
(沈陽理工大學自動化與電氣工程學院,遼寧 沈陽110159)
姿態解算在飛行器動力學計算中具有舉足輕重的地位。姿態解算的精度和速度會直接影響飛行控制算法的穩定行、可靠性和實現的難易程度,因此對飛行器姿態解算方法的研究具有重要意義。目前,通常采用陀螺儀獲得飛行器的姿態角,但是長期測量精度較差,因此需要對陀螺儀的輸出數據進行有效的處理才能獲得可靠和穩定的姿態角信息,陀螺儀輸出的數據通過運動學微分方程可以推導出飛行器的微分方程[1]。
在飛行力學研究中,用于求解歐拉角的微分方程中包含大量的三角運算,會給實時解算帶來了一定的困難,而且存在的“GimbalLock”現象[2]。所以歐拉角方法不適用于全姿態飛行器的姿態確定。本文引入四元數,進而使用了一階龍哥庫塔求解四元數微分方程,最終轉化為歐拉角得到飛行器空中姿態。
1 坐標變換
首先進行坐標變換,利用歐拉角描述一次平面旋轉,見圖1.

圖1 坐標系間的變換關系[3]
設坐標系繞旋轉α角后得到坐標系X2OY2,空間中有一個矢量在坐標系X1OY1中的投影為rx2,在X2OY2內的投影為ry2,由于旋轉繞進行,所以Z坐標未變,即有:

上面僅僅是繞一根軸的旋轉,三維空間中的歐拉角要進行三次這樣的坐標旋轉變換,得到(2)式。

2 求解姿態角
經過三次旋轉,到了一個表示旋轉的方向余弦矩陣。再利用歐拉微分方程,進行下面的姿態解算:
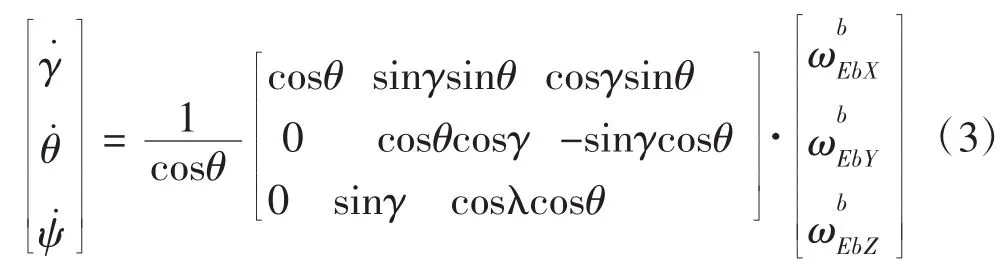
式(3)左邊是本次更新后的翻滾角 Φ(roll)、俯仰角 θ(pitch)、偏航角 ψ(yaw),式(3)右邊是上個周期測算出來的角度,角速度單位為弧度,計算間隔時T陀螺角速度。因此求解這個微分方程就能解算出當前的歐拉角。
3 利用四元數求解姿態角
利用四元數代替歐拉角對方向余弦矩陣的描述:

引入一階龍哥庫塔方程并求解。最后根據四元數方向余弦陣和歐拉角的轉換關系,把四元數轉換成歐拉角,進而得到用四元數表示的四軸飛行器空中姿態參數 γ、θ、ψ:

4 實驗結果
根據上述推算方法進行實驗,并在飛行器上位機上采集到如下數據。結果如圖2和圖3所示。其中加速度曲線橫坐標表示時間(ms);縱坐標表示加速度(g)。陀螺儀曲線橫坐標表示時間(ms);縱坐標表示陀螺儀(%)。

(續下圖)
(接上圖)

圖 2 分別為加速度 X(g)、Y(g)、Z(g)曲線

圖3 陀螺儀X、Y、Z軸曲線
5 結束語
本文對歐拉角的姿態解算進行改進,引入四元數進行解算。一方面避免了利用歐拉方程中的復雜三角運算,另一方面解決了俯仰角為90°時方程式會出現的“GimbalLock”現象。經過試驗驗證該方法進行姿態解算效率高而且結果準確,在姿態解算領域有良好的應用前景。
參考文獻:
[1]張 帆,曹喜濱,鄒經湘.一種新的全角度四元數與歐拉角的轉換算法[J].南京理工大學學報(自然科學版),2002(04):376-380.
[2]趙學杰.數值方法中Runge-Kutta方法改進的探討[J].衡水學院學報,2014,16(04):23-26.
[3]呂志鵬,伍吉倉,公 羽.基于四元數的大旋轉角坐標變換模型的改進[J].武漢大學學報(信息科學版),2016(02):1-7.

