中心口錐底料罐中離散顆粒卸料特性的實驗與仿真研究

郭健瑋，孔建益，王興東，盛漢橋

(1.武漢科技大學冶金裝備及其控制教育部重點實驗室，湖北 武漢，430081； 2.中冶南方工程技術有限公司，湖北 武漢，430223)

離散顆粒是自然界中廣泛存在的一種物質形態。與常規的氣體、液體和固體不同，顆粒材料是由大量單體顆粒相互作用而形成的復雜體系。在一定條件下顆粒會發生類固—液或類氣—液轉換，其中類固—液轉換過程及其力學行為是顆粒物質相關研究的熱點。

Cundall等[1]提出的離散單元法(discrete element method，DEM)是一種可針對每個顆粒進行數值求解的計算方法，因模擬精度高、獲取微觀信息多等優點已被廣泛應用。Yang等[2]通過二維數值模擬觀察到由顆粒卸料時不斷形成和斷裂的動態拱引起的楔形料罐周期性振動現象。Anand等[3]分析了料罐壁面材料等單一變量對中心楔形料斗卸料速率的影響規律。Liu等[4]研究了平底料罐內顆粒的流動特性及卸料速率。譚援強等[5]采用離散元法對塑料球在筒倉內的流動進行數值模擬，考察了錐形料罐下部孔徑等參數對中心筒倉卸料流態的影響。張西良等[6]對中心圓錐料罐中粉體物料的流動特性進行仿真分析，探討了顆粒物理屬性與顆粒流動性的關系。許鵬凱等[7]分析了楔形中心和偏心料倉中壁面摩擦系數對卸料速率的影響。

本文主要研究顆粒物料在中心口圓錐底料罐中的卸料特性。首先采用離散單元法針對罐內顆粒受力情況建立模型，并在EDEMTM顆粒系統仿真分析軟件平臺上進行數值模擬分析，然后通過實驗對比來驗證模型的準確性，最后基于仿真模型對顆粒材料卸料特性的影響因素進行探討。

1 顆粒力學模型的建立及實驗驗證

1.1 離散單元力學模型

對單一顆粒而言，其運動主要受到自身重力、顆粒之間的碰撞力或壁面對顆粒的作用力這幾方面的影響。圖1所示為顆粒受力情況。

(a)

(b)

圖1顆粒受力分解示意圖

Fig.1Schematicdiagramofforcesexertedontheparticles

基于軟球模型和Hertz-Mindlin接觸模型對顆粒進行受力分析。圖1(a)中，顆粒i與顆粒j之間的碰撞力包括法向力Fn,ij和切向力Ft,ij，即：

Fij=Fn,ij+Ft,ij

(1)

根據胡克定律，顆粒i所受法向力Fn,ij的計算公式為：

Fn,ij=fcn,ij+fdn,ij

(2)

fcn,ij(t)=fcn,ij(t-Δt)-knΔδn

(3)

(4)

式中：fcn,ij為法向彈性力；fdn,ij為法向阻尼力；kn為法向彈性系數；ηn為法向阻尼系數；δn為顆粒間的法向相對位移；t為卸料時間。

顆粒i所受切向力Ft,ij的計算公式為：

(5)

fct,ij(t)=fct,ij(t-Δt)-ktΔδt

(6)

(7)

式中：fct,ij為切向彈性力；fdt,ij為切向阻尼力；kt為切向彈性系數；ηt為切向阻尼系數；δt為顆粒間的切向相對位移；μp為顆粒間摩擦系數。

料罐內的顆粒運動屬于稠密固相流動，對單一顆粒而言，周圍顆粒的存在不僅縮小了其流動區域，同時也會使顆粒與顆粒間、顆粒與壁面間發生碰撞，故單一顆粒i所受合力為：

(8)

圖1(b)中，顆粒k受到壁面的作用力包括法向合力Fn,w k及切向摩擦力Ff。Fn,w k的計算公式為：

Fn,w k=fcn,w k+fdn,w k

(9)

fcn,w k(t)=fcn,w k(t-Δt)-knΔδn

(10)

(11)

式中：fcn,w k、fdn,w k為壁面w對顆粒k作用在法向上的彈性力和阻尼力。

顆粒k所受重力及其他顆粒在法向上的作用力之和為：

(12)

已知壁面傾角為β，則顆粒受到的切向摩擦力為：

(13)

式中：μ為顆粒與壁面的摩擦系數。

1.2 仿真模型

根據上述離散單元力學模型，在EDEMTM顆粒系統仿真分析軟件平臺上搭建仿真模型。選用根據高爐爐頂料罐簡化的中心口圓錐底料罐作為顆粒載體，如圖2所示，其由圓錐料斗及圓柱筒體兩部分組成，保持卸料口尺寸不變，通過改變料罐半錐角α來調控料罐結構。為了便于觀察罐體內部顆粒流動情況，在料罐中安裝擋料板將其一分為二，建立半罐模型。

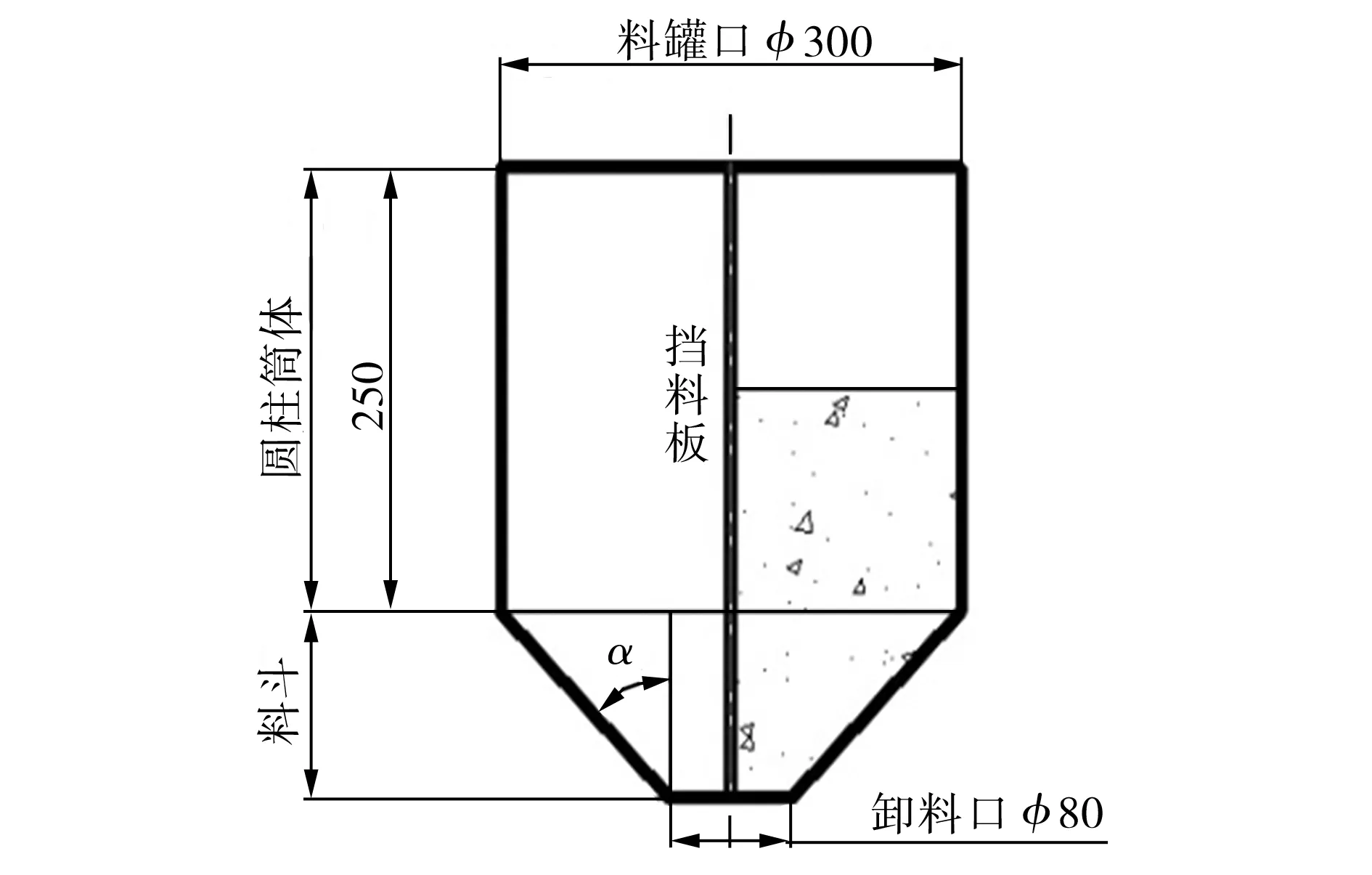
圖2 料罐結構示意圖

為減小顆粒復雜結構形態對卸料工序的影響程度，將顆粒模型定義為直徑6 mm、質量0.15 g的球體，材質為聚乙烯，并且顆粒運動過程中的受力及位移、速度等均由其自身與接觸體碰撞產生的彈性形變所引起。聚乙烯顆粒間的摩擦系數、彈性恢復系數等均根據聚乙烯物性參數、顆粒模型的形狀和尺寸等從GEMM數據庫[8]中選取，具體參數取值如表1所示。

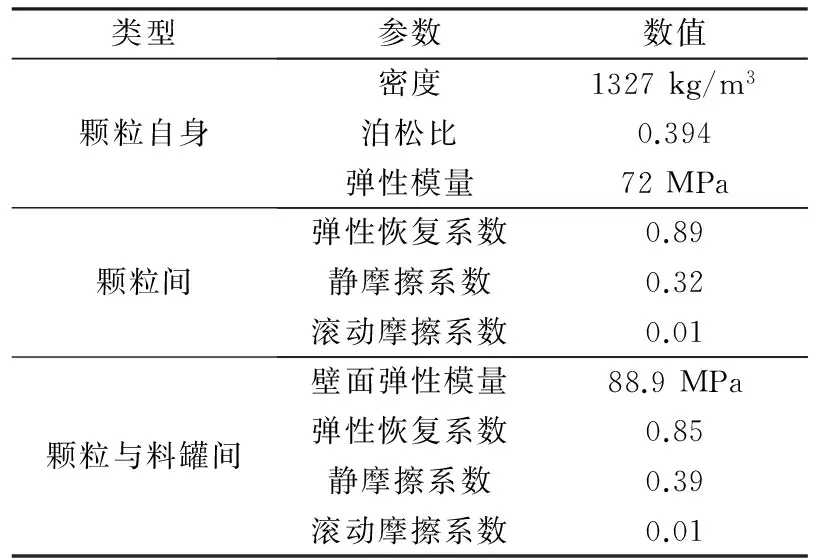
表1 塑料球和料罐的物性參數

在料罐頂部設置顆粒工廠，顆粒初始速度為零，受重力以“落雨法”[9]自然堆積于料罐內。當達到預定顆粒數時停止生成顆粒，待顆粒靜置至穩定狀態后打開閥門進行卸料，直至所有顆粒離開料罐，記錄相關數據。

觀察圖3所示卸料過程中的顆粒速率分布云圖可知，卸料口處顆粒的軸向速率較高，而靠近料罐壁面的顆粒速率較低，在壁面附近形成死區，罐內顆粒的整體流動呈現出中心流趨勢。

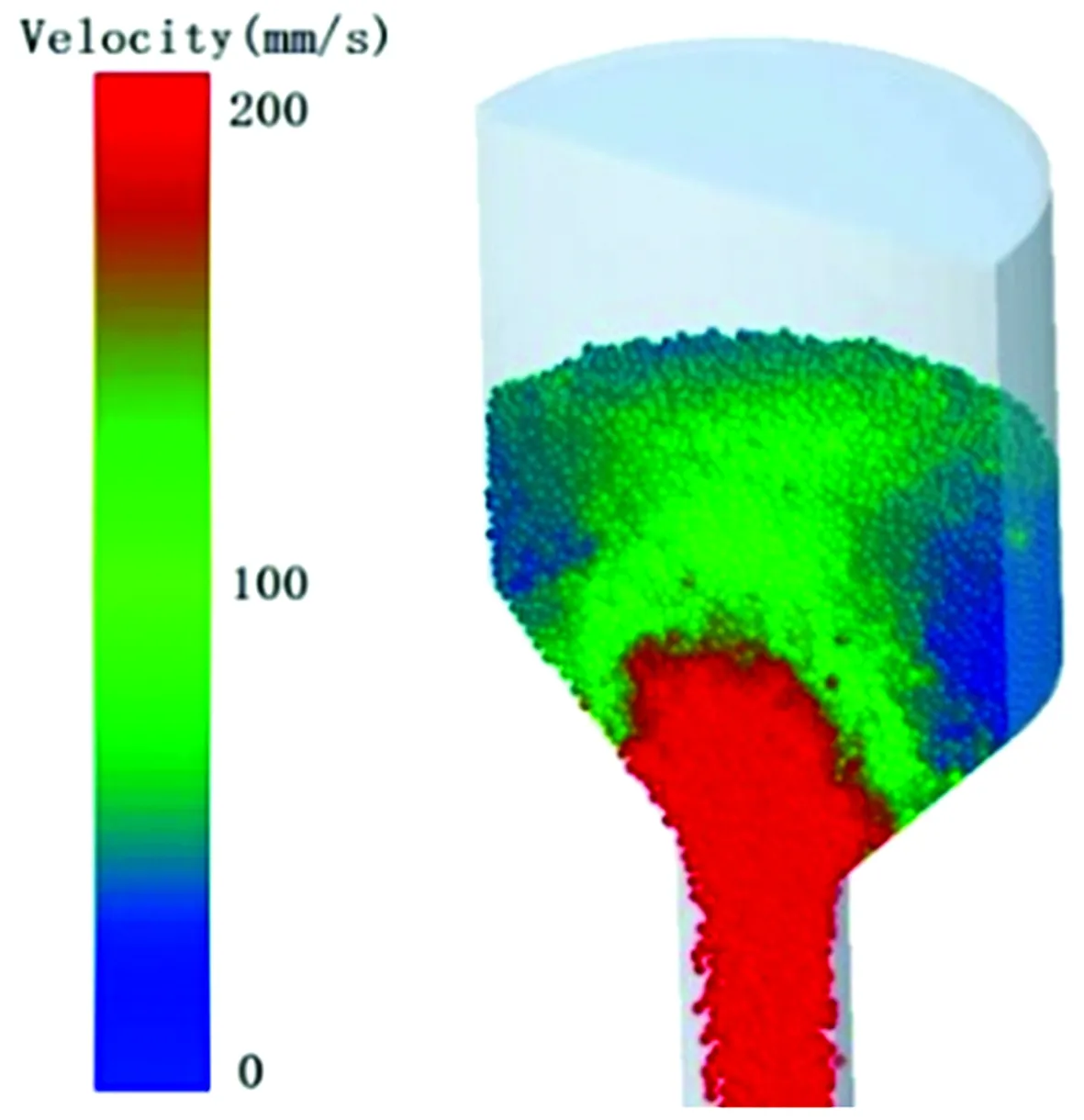
圖3 顆粒軸向速率分布

1.3 實驗驗證

搭建與仿真模型相同尺寸的料罐進行卸料實驗。實驗裝置由料罐、平板閥、顆粒收集桶、圖像采集裝置4個部分組成(見圖4)。為方便觀測，料罐采用有機玻璃制作。圖像采集裝置使用索尼RX100V高速相機，最高分辨率為5472×3648，快門速度可達1/2000 s，確保圖像采集不失真。

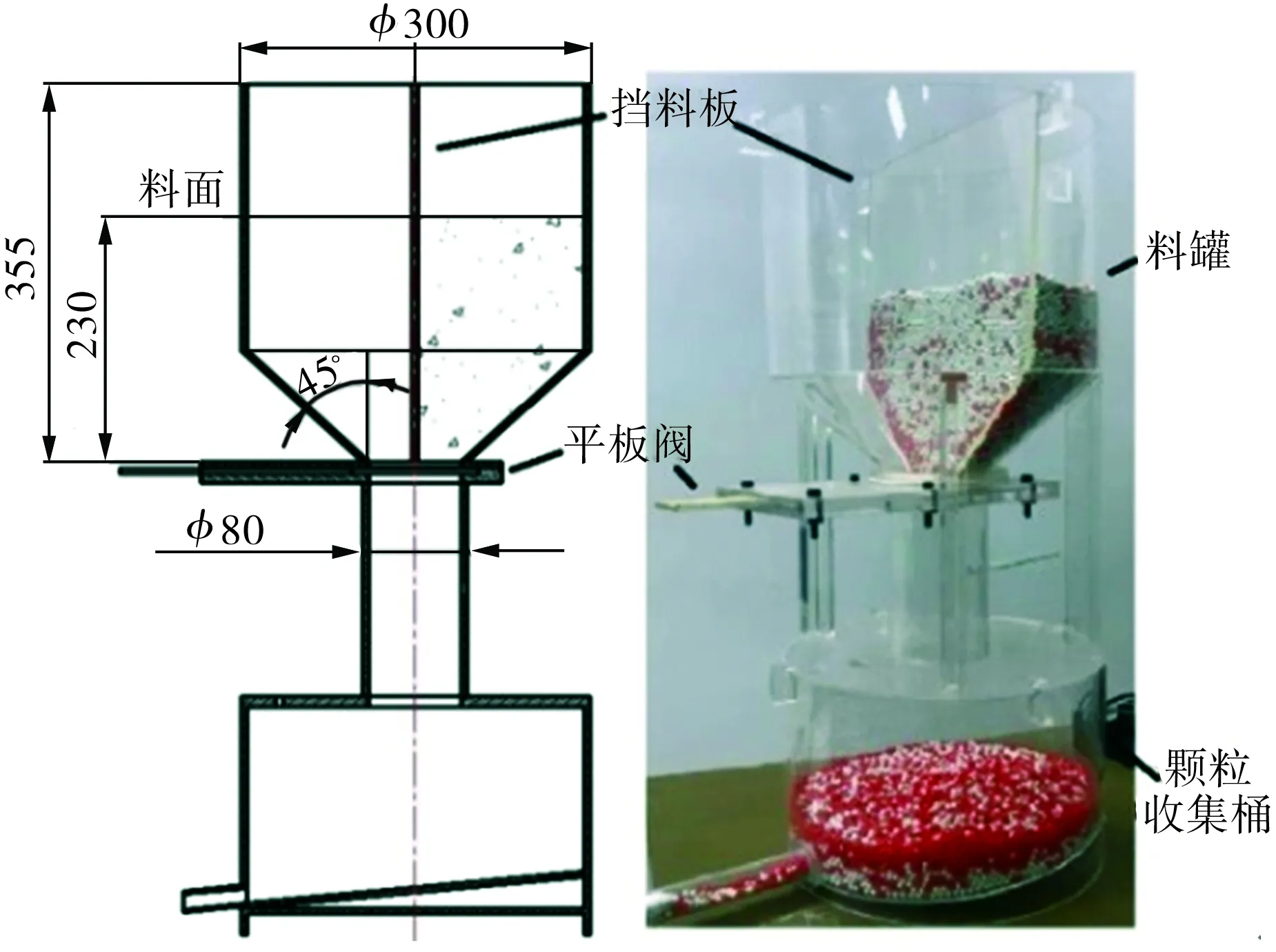
圖4 實驗裝置

實驗開始前準備顆粒材料，取與仿真模型中相同規格的紅、白兩色聚乙烯塑料球共計35 000顆。對塑料球稱量計數，紅、白兩色各分成質量相同的4組顆粒。關閉平板閥，將兩種顆粒交替逐層均勻鋪撒于料罐內。相機設為動態追蹤模式，每秒采集100幅圖像。實驗與仿真中的顆粒數量、分布及卸料工況相同。設閥門開啟時為0 s，從一側向擋料板方向觀察料罐中顆粒的流動情形，如圖5所示。閥門開啟1.0 s時，實驗結果中第一層紅色顆粒已經有一半離開料罐，第二層紅色顆粒出現“凹陷”且中間位置即將接近卸料口；對比同一時刻的仿真結果，第一層紅色顆粒的流動狀態與實驗結果幾乎相同，而第二層紅色顆粒剛剛到達卸料口位置。閥門開啟1.5 s時，實驗結果中第一層紅色顆粒幾乎完全離開料罐，只有少量靠近壁面的顆粒在卸料口處滯留，第三層中心位置紅色顆粒剛運動至卸料口，同時第四層紅色顆粒開始“凹陷”；同一時刻的仿真結果中，第一、二層紅色顆粒運動狀態幾乎與實驗一致，第三層中心位置紅色顆粒已開始通過卸料口。閥門開啟2.5 s時，實驗結果中罐內顆粒已經完全進入圓錐料斗區域，第一層紅色顆粒已完成卸料，第四層紅色顆粒運動至卸料口位置；同一時刻的仿真結果與實驗結果十分吻合。總之，數值模擬與實驗中對應時刻觀察到的顆粒流動形態相差甚微，表明本文所建立的離散單元力學模型和仿真模型可以比較準確地描述中心口圓錐底料罐的顆粒卸料過程。

圖5 顆粒卸料過程的實驗與模擬結果對比

2 離散顆粒卸料特性影響因素分析

為了進一步揭示料罐內顆粒卸料特性，在前面的仿真模型基礎上去掉擋料板，建立整罐模型，然后分析料罐半錐角及顆粒形狀和物性參數等對顆粒運動速率和顆粒間作用力的影響。

2.1 料罐半錐角對卸料的影響

料罐材料對卸料過程影響非常小[3]，然而料罐結構參數與卸料時的顆粒流態關系明顯。針對料罐半錐角α的研究[10]表明，當α>45°時卸料流態呈現為中心流，而當α<45°時卸料流態呈現為整體流。但是料罐半錐角對顆粒卸料速率及顆粒間擠壓情況的影響規律還缺乏較為清晰的描述。

參照圖2，將料罐結構中的擋料板去掉，分別取半錐角α為15°、30°、45°、60°和75°，對5個整體料罐進行卸料仿真分析。對于每個料罐模型，頂部的顆粒工廠均生成70 000個球形顆粒，并沉降于料罐內靜置至穩定狀態，作為仿真的初始條件。從卸料閥開啟到顆粒全部離開料罐為一個完整的仿真過程。卸料閥開啟時間為0 s。在整體料罐仿真模型的卸料口設置采集網格，當顆粒進入采集區域時記錄其軸向速率，且每個顆粒進入該區域只記錄一次，當顆粒離開網格時視為排出料罐，達到空倉狀態時，停止數據采集。

圖6為半錐角不同時料罐中顆粒離開卸料口時的軸向平均速率。由圖6可見，閥門打開后顆粒的軸向速率迅速提高，且半錐角越大，顆粒速率提升幅度越小。α=15°時，顆粒軸向速率最高達1035 mm/s，而α=75°時，顆粒軸向速率最高僅達到372 mm/s。另外，當顆粒速率達到最大值后，在一段時間內維持相對穩定，這一趨勢在半錐角較小的料罐模型中表現較為明顯。

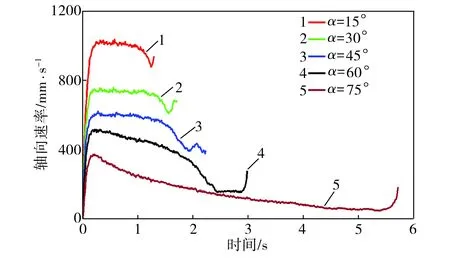
圖6不同半錐角料罐中顆粒離開卸料口時的軸向速率

Fig.6Axialvelocityofparticlesatthehopperoutletofsiloswithdifferenthalfconeangles

由圖6還可以看出，隨著顆粒逐漸離開料罐，其軸向平均速率開始降低。當料罐內顆粒即將全部排出時，剩余顆粒又開始加速運動離開料罐，對應于圖6中的速率曲線最后一段都出現急速上升的現象。對比5個料罐的排料時間，15°半錐角料罐最快完成卸料，耗時1.31 s，而30°、45°、60°、75°半錐角料罐卸料耗時分別為1.73、2.25、3.01、5.75s。

由于碰撞力會影響顆粒的運動速度，故采集料罐內所有顆粒受到的平均擠壓力，如圖7所示。卸料閥開啟后，罐內顆粒受到的擠壓力隨罐內顆粒總量的減少而下降，在料罐卸料末期顆粒間擠壓力趨近于零，這與圖6中顆粒速率在最后時段急速上升的現象相對應。

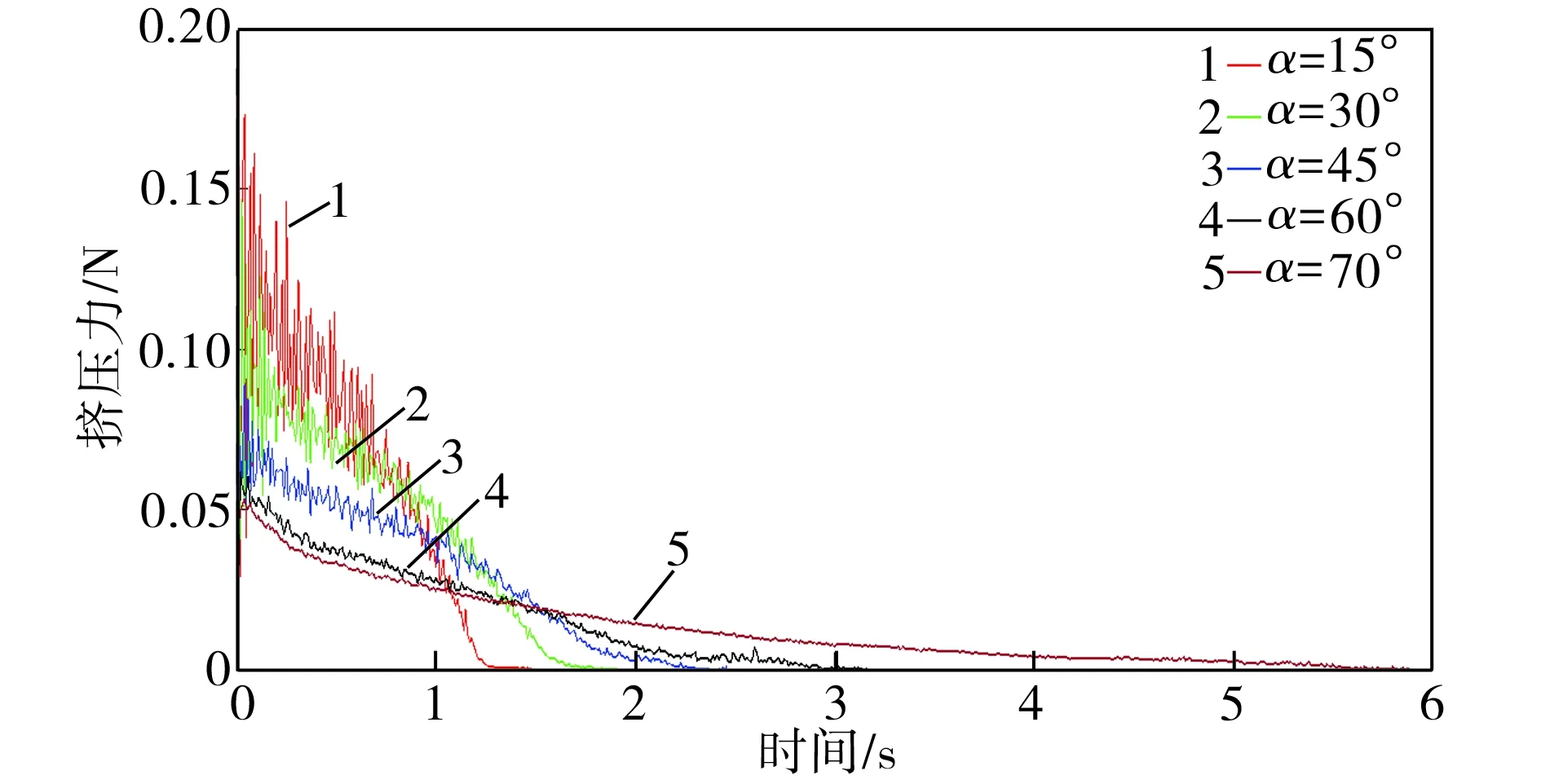
(a)卸料全過程

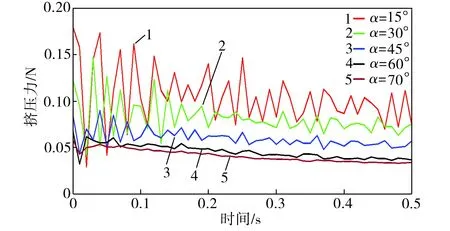
(b)卸料閥開啟0.5 s內

Fig.7Excursionforceofparticlesinthesiloswithdifferenthalfconeangles

由圖7(b)可見，隨著料罐半錐角的增大，顆粒間擠壓力的變化幅度減小，這表明顆粒間的擠壓趨于平緩。經計算可得，15°～75°半錐角料罐內顆粒擠壓力的平均變化幅值分別為0.068、0.061、0.032、0.021、0.016 N。

2.2 顆粒特性對卸料的影響

顆粒材料自身的物性參數也是影響其卸料特性的重要因素，例如高爐原料中鐵礦石與焦炭的顆粒性質差別較大，研究其卸料過程對于高爐上料工藝設計以及保證原料的顆粒完整性等有重要意義。

鐵礦石多為球形顆粒，而焦炭多為立方體顆粒。與球形顆粒相比，立方體顆粒運動方式更多樣，顆粒間接觸更為復雜。為模擬立方體焦炭顆粒，本文設置4×4×4間距為1 mm的基點組成立方體，使用直徑2 mm的球元進行填充建模，其外形結構見圖8。

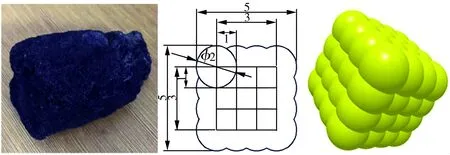
圖8 立方體焦炭顆粒仿真模型

分別取相同數量(70 000顆)的球形鐵礦石顆粒、球形焦炭顆粒和與球形焦炭顆粒相同質量的立方體焦炭顆粒于α=45°的料罐中進行整罐卸料過程仿真，焦炭和鐵礦石顆粒的物性參數從GEMM數據庫中調取，如表2所示。

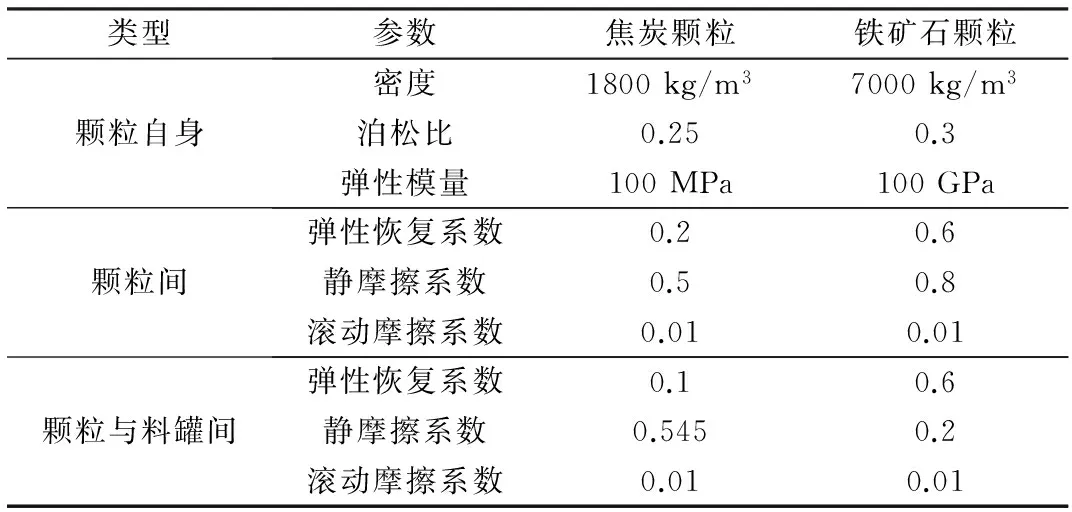
表2 焦炭和鐵礦石顆粒的物性參數

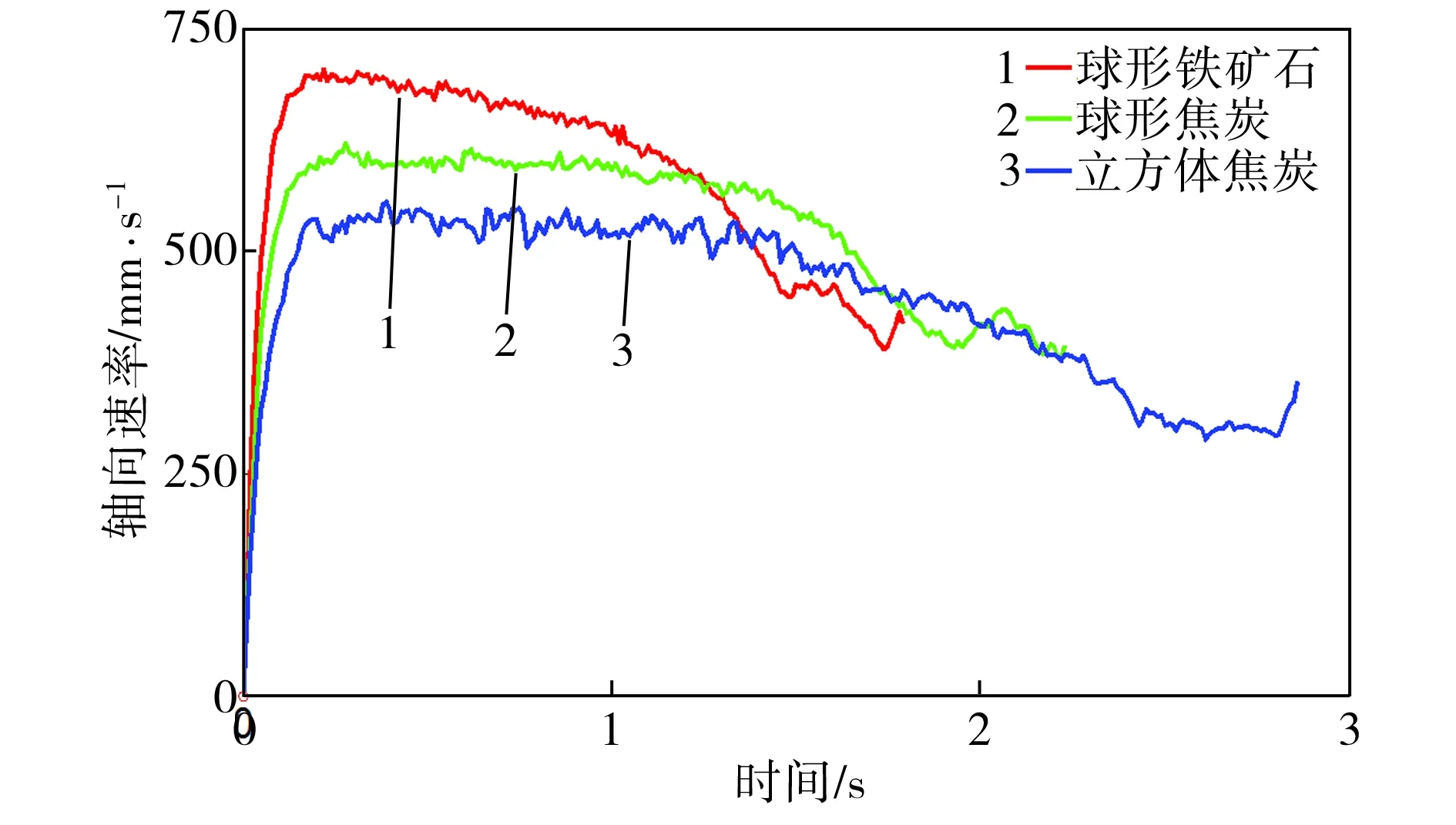
圖9給出了上述3種顆粒在卸料過程中離開卸料口時的軸向速率及顆粒間擠壓力的變化情況。由圖9(a)可見，卸料初始階段，球形鐵礦石、球形焦炭和立方體焦炭顆粒的軸向速率均迅速上升，其分別達到最大值703、611、554 mm/s后維持相對穩定，然后卸料速率隨顆粒的排出而緩慢下降；在卸料結束階段，球形鐵礦石顆粒和球形焦炭顆粒的軸向速率相差不大，但立方體焦炭顆粒的速率曲線出現了明顯的上升階段。對比3種顆粒的卸料時間，球形鐵礦石顆粒最快完成排料，耗時1.81 s，球形和立方體焦炭顆粒分別耗時2.25 s和2.89 s。

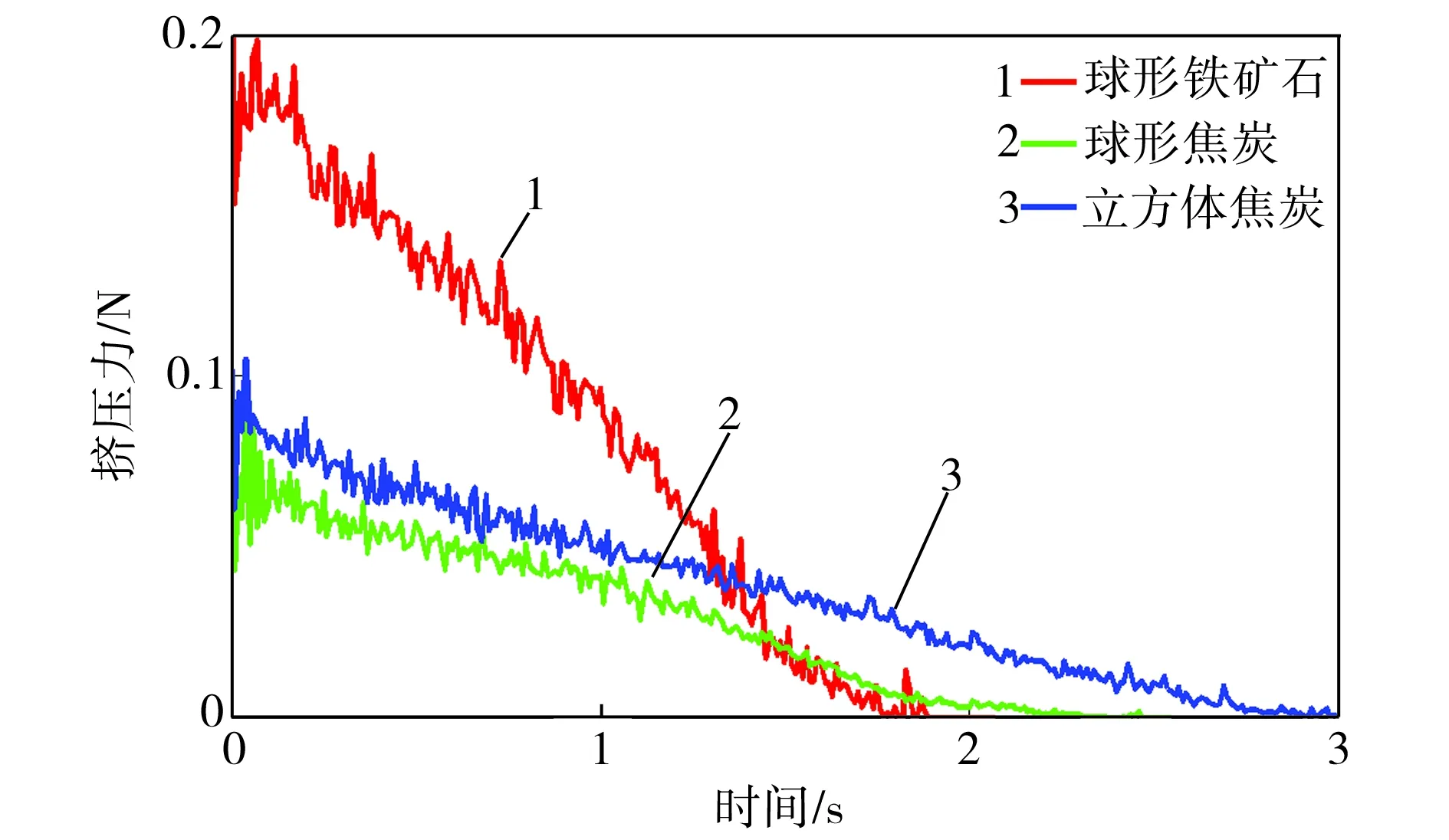
結合圖9(b)可見，卸料閥開啟后，球形鐵礦石顆粒所受擠壓力最大、總體下降速率最快；立方體焦炭顆粒所受擠壓力次之，但卸料持續時間最長。在卸料閥開啟后的前1.0 s內，球形與立方體焦炭顆粒所受擠壓力變化曲線幾乎保持平行，但1.0 s后球形顆粒的擠壓力降速提高，且該現象在1.5 s后尤為明顯，此時球形焦炭顆粒與鐵礦石顆粒的擠壓力下降速率幾乎一致。而立方體焦炭顆粒的擠壓力總體呈線性下降，表明其擠壓力變化較為平穩。統計數據顯示，在卸料階段的前1.0 s內，鐵礦石、立方體焦炭和球形焦炭這3種顆粒的平均擠壓力幅值變化分別為0.094、0.048、0.041 N，即鐵礦石顆粒擠壓力幅值變化最大，而兩種焦炭顆粒的擠壓力幅值變化較為接近，且立方體顆粒較球形顆粒要略高一點。

(a)軸向速率

(b)擠壓力

圖9鐵礦石和焦炭顆粒離開卸料口時的軸向速率和顆粒擠壓力

Fig.9Axialvelocityofironoreandcokeparticlesatthehopperoutletandexcursionforceamongthem

以上分析表明，對于相同形狀的不同材料顆粒，材料密度越大，其動能和受到的擠壓力也越大，整體卸料時間越短；對于材料相同而形狀不同的顆粒，由于立方體顆粒間存在面-面、點-面、點-線等多種接觸方式，比球狀顆粒的點接觸方式更為復雜，因此宏觀上表現出擠壓力和摩擦阻力更大，從而導致立方體顆粒所需的卸料時間更長。

3 結論

(1)對中心口錐底料罐半罐模型的仿真和實驗對比，驗證了基于離散單元法建立的顆粒力學模型的準確性。

(2)料罐半錐角越小時，卸料口處顆粒軸向運動速率越高，所需卸料時間越少，顆粒間的擠壓力越大，而且擠壓力變化越劇烈。

(3)在相同料罐中，球形顆粒的密度越大，顆粒間擠壓力也越大，擠壓力幅值變化越劇烈，同時顆粒在卸料口處的軸向速率也越高，所需卸料時間越短。

(4)與球形顆粒相比，由于接觸方式復雜，立方體顆粒間的擠壓力更大，其在卸料口處的軸向速率相對較慢，所需卸料時間更多。

參考文獻

[1] Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J].Géotechnique, 1979, 29(1):47-65.

[2] Yang S C, Hsiau S S. The simulation and experimental study of granular materials discharged from a silo with the placement of inserts[J].Powder Technology, 2001, 120(3):244-255.

[3] Anand A, Curtis J S, Wassgren C R, et al. Predicting discharge dynamics of wet cohesive particles from a rectangular hopper using the discrete element method (DEM)[J].Chemical Engineering Science, 2009, 64(24):5268-5275.

[4] Liu S D, Zhou Z Y, Zou R P, et al. Flow characteristics and discharge rate of ellipsoidal particles in a flat bottom hopper[J].Powder Technology, 2014, 253:70-79.

[5] 譚援強,鄭軍輝,張浩,等.基于離散元法的錐形筒倉中顆粒流體的數學模擬[J].過程工程學報,2015, 15(6):916-922.

[6] 張西良,張建,李萍萍,等.粉體物料流動性仿真分析[J].農業機械學報, 2008, 39(8):196-198.

[7] 許鵬凱,段學志,錢剛,等.楔形中心和偏心料倉中壁面摩擦系數對卸料速率的影響[J].化工學報,2015, 66(3):880-887.

[8] Generic EDEM Material Model (GEMM) Database[DB/OL].[2018-01-05].http://www.edemsimulation.com/ gemm.

[9] 孫其誠,厚美瑛,金峰.顆粒物質物理與力學[M].北京：科學出版社,2011：242-265.

[10] Schulze D. Powders and bulk solids: behavior, characterization, storage and flow[M].Berlin, Heidelberg: Springer-Verlag, 2008.