地質雷達信號分析的雙正交小波預測反褶積法

凌同華 劉浩然 谷淡平 張亮

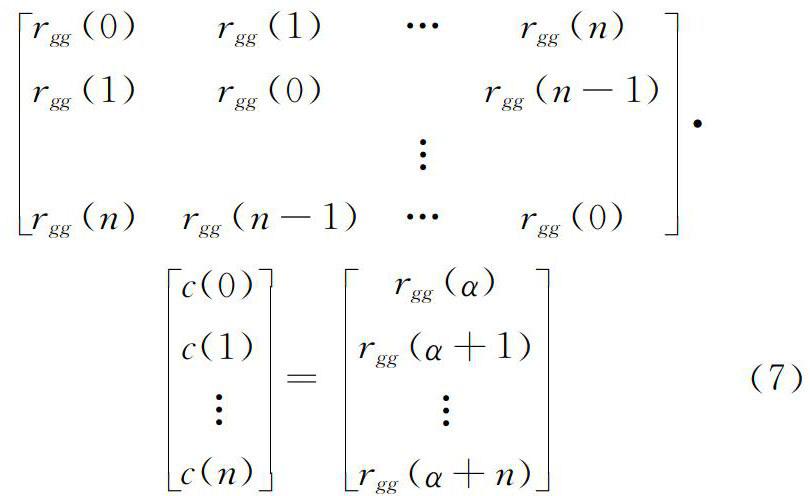
摘要：為了降低電磁波衰減、噪聲干擾等因素對地質雷達檢測效果的影響，提出一種雙正交小波預測反褶積法（PDBW法）。在PDBW法中，針對地質雷達檢測信號選取具有最小重構誤差的雙正交小波基，運用該小波基將地質雷達檢測信號分解成不同頻段的時域子信號，對各頻段的時域子信號進行預測反褶積等濾波處理，再對處理后的子信號進行重構變換，得到PDBW法的處理結果。將PDBW法用于實驗檢測信號處理，并將處理結果與預測反褶積法的處理結果進行比較，結果表明：PDBW法能有效壓制多次回波干擾，準確識別深部信號，顯著提高深部信號信噪比，從而進一步改善了地質雷達探測分辨率和圖像分析的準確性。

關鍵詞：地質雷達；雙正交小波分析；預測反褶積；探測分辨率；信噪比

中圖分類號：TN959.71 文獻標志碼：A文章編號：16744764（2018）02002606

收稿日期：20170615

基金項目：國家自然科學基金 （51678071、51278071）；長沙理工大學橋梁工程領域開放基金（14KC06）；長沙理工大學研究生科研創新項目（CX2015BS02）

作者簡介：凌同華（1968），男，教授，博士生導師，主要從事隧道與地下工程研究，Email：lingtonghua@163.com。

Received：20170615

Foundation item：National Natural Science Foundation of China （No. 51678071， 51278071）； Open Fund of Bridge Engineering of Changsha University of Science and Technology （No. 14KC06）； Graduate Research and Innovation Project of Changsha University of Science and Technology （No. CX2015BS02）

Author brief：Ling Tonghua （1968）， professor， doctoral supervisor， main research interests： tunnel and underground engineering， Email：lingtonghua@163.com.A predictive deconvolution method based on biorthogonal

wavelet of GPR signal analysis

Ling Tonghua， Liu Haoran， Gu Danping， Zhang Liang

（School of Civil Engineering and Architecture， Changsha University of Science & Technology， Changsha 410114， P. R. China）

Abstract：In order to reduce the influence of some factors such as the electromagnetic wave attenuation and noise jamming on detection effect of GPR， a predictive deconvolution method based on biorthogonal wavelet was proposed （short for PDBW method）. In the PDBW method， the biorthogonal wavelet basis with the minimum reconstruction error for detection signal of GPR was chosen， using this wavelet to decompose the GPR signals into different frequency band subsignals， and then predictive deconvolution and other filter method were used to deal with each frequency band subsignal in time domain， at last the results of PDBW method by reconstructing each subsignal were get. Using the PDBW method to deal with the detection signal of experiment， the results show that， comparing with the predictive deconvolution， the PDBW method can restrain the multiple echo interference， identify the deep signal precisely， and enhance the signal to noise ratio of deep signal， thus improving the detecting resolution and the accuracy of image analysis of GPR signal.

Keywords：ground penetrating radar；biorthogonal wavelet analysis；predictive deconvolution；detecting resolution；signal to noise ratio

地質雷達具有無損、分辨率高、操作便捷等優點[12]，被廣泛用于隧道超前預報、地下管網探測、工程結構檢測等眾多領域[35]。在檢測過程中，高頻電磁波的衰減、多次回波的干擾及檢測目標尺寸等因素均會影響地質雷達信號的探測分辨率和圖像的最終解釋效果。

目前，提高雷達探測分辨率的主要方法有：預測反褶積、基于模糊分析的脈沖反褶積、基于最大峰度法的時變反褶積和地層頻譜校正等，通過壓縮雷達子波和壓制多次回波等方式，上述方法能有效改善地質雷達信號的處理效果[611]。然而，當深部信號的信噪比受多次回波干擾而降低時，以上方法很難在壓縮子波和抑制回波干擾的同時提高深部信號的信噪比，甚至會導致深部信號丟失并造成錯誤的圖像解釋。由于小波分析能夠將信號分解成不同頻段的時域子信號，在含反射波信息的子信號中，噪聲的頻段和幅值能量能得到有效控制。因此，對該子信號進行預測反褶積處理便可得到深部信號的反射系數，從而，在抑制多次回波的同時提高深部信號信噪比。

本文以此為切入點，提出一種雙正交小波預測反褶積法。該法針對地質雷達信號選取具有最小重構誤差的雙正交小波基，運用該小波基對地質雷達檢測信號進行不同頻段的分解和重構，并對各頻段的時域子信號進行預測反褶積等濾波處理，再對處理后的子信號進行重構變換，從而得出該法的處理結果。與預測反褶積法相比，該法能有效壓制多次回波，準確識別深部信號，顯著提高深部信號信噪比，從而進一步提高地質雷達的探測分辨率和圖像分析的準確性。

第2期 凌同華，等：地質雷達信號分析的雙正交小波預測反褶積法1基本原理

1.1雙正交小波的分解與重構

令f∈L2（R），φj，k、φj，k分別為j層的分解尺度函數和分解小波函數，對信號f（t）進行雙正交小波分解，信號f（t）的小波分解系數為[12]aj，k=[f，φj，k]

dj，k=[f，φj，k]（1）式中：aj，k、dj，k分別為j層小波分解的近似系數和細節系數。

式（1）中aj，k、dj，k應滿足aj+1，k=[aj，k，φj+1，k]

dj+1，k=[aj，k，φj+1，k] （2）令j，k、j，k分別為j層的重構尺度函數和重構小波函數，則雙正交小波分析中的重構公式為[13]aj，k=[aj+1，k，j+1，k]+[dj+1，k，j+1，k]（3）1.2預測反褶積法

令預測濾波因子為c（t），時間延遲為n，預測步長為α，地質雷達信號的過去值為f（t-1），f（t-2），…，f（t-n），現在值為f（t），t+α時刻的實際將來值為f（t+α）。

運用反褶積求取t+α時刻的預測值為（t+α）=c（t）g（t）=∑nτ=0c（τ）g（t-τ） （4）預測誤差為ε（t+α）=f（t+α）-（t+α） （5）在最小平方反濾波理論中，當誤差的平方和取最小值時，預測值接近實際值，則式（5）可改寫成c（s）[∑n+αt=0ε2（t+α）]=0 （6）按照Toeplitz矩陣，濾波因子c（t）的求解形式為[14]rgg（0）rgg（1）…rgg（n）

rgg（1）rgg（0）rgg（n-1）

rgg（n）rgg（n-1）…rgg（0）·

c（0）

c（1）

c（n）=rgg（α）

rgg（α+1）

rgg（α+n）（7）將解出的c（t）代入式（5）后，再取Z變換，可得E（z）=F（z）A（z）（8）其中A（z）=1-z-αc（z）（9）在式（8）、式（9）中，z-αE（z）、F（z）、c（z）分別為預測誤差ε（t+α）、f（t）和c（t）的Z變換。對A（z）做逆Z變換，可得預測誤差濾波因子a（t）=[1，0，0，…，0，-c（1），…，-c（n）]（10）運用a（t）對地質雷達原始數據進行反褶積，得到信號的反射系數序列，即預測反褶積法的計算結果。

2雙正交小波預測反褶積法

2.1雙正交小波預測反褶積法的基本原理

根據雙正交小波的分解重構變換和預測反褶積法，提出了一種改進的反褶積法，即雙正交小波預測反褶積法（predictive deconvolution based biorthogonal wavelet analysis，簡稱PDBW法）。該方法的基本原理如下：

根據式（1）、式（2），對信號f（t）進行j層小波分解，得到如下小波分解系數為d1，k=[f，φ1，k]

d2，k=[a1，k，φ2，k]

dj，k=[aj-1，k，φj，k]

aj，k=[aj-1，k，φj，k] （11）在式（11）中，運用式（3）分別對各層系數進行小波重構，可得式（12）[13]。fd1，k=[d1，k，1，k]

fd2，k=[[d2，k，2，k]，1，k]

fdj，k=[[[dj，k，j，k]，j-1，k]…，1，k]

faj，k=[[[aj，k，j，k]，j-1，k]…，1，k]（12）式中：fdj，k、faj，k分別為第j層系數重構的時域子信號。

按照式（4）～式（10），對各時域子信號進行預測反褶積，得到式（13）所示反射系數序列。ξd1（t）=[ad1（k），fd1（t-k）]

ξd2（t）=[ad2（k），fd2（t-k）]

ξdj（t）=[adj（k），fdj（t-k）]

ξaj（t）=[aaj（k），faj（t-k）]（13）對式（13）中的各反射系數序列進行重構變換[15]，可得ξf=ξaj⊕ξdj⊕…ξd2⊕ξd1 （14）式中：ξf為PDBW法處理后的地質雷達信號。

2.2雙正交小波預測反褶積法的應用流程

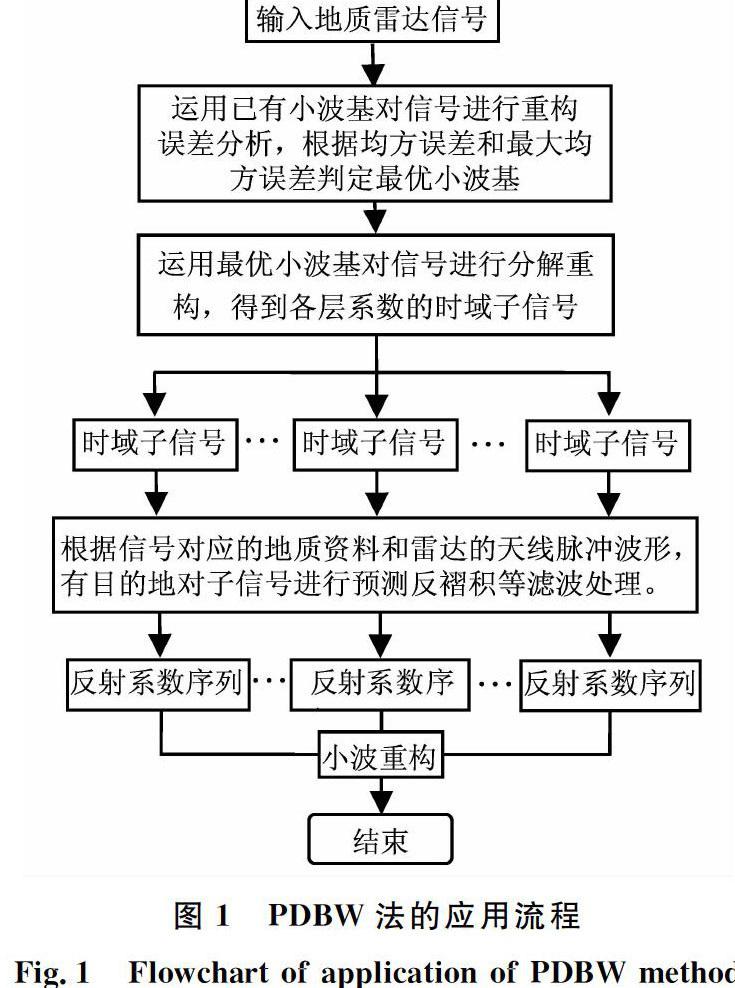
運用PDBW法處理地質雷達原始信號時，為了得到好的處理結果，應按照PDBW法的具體流程對信號進行處理，該法的應用流程見圖1。

圖1PDBW法的應用流程

Fig.1Flowchart of application of PDBW method此外，在PDBW法的應用過程中，還應遵從以下幾個關鍵步驟：

1）最優小波基的選取不同小波基分析同一信號會產生不同的結果。在PDBW法中，小波分析的主要目的是對信號進行不同頻段的小波分解和重構，因此，為了確保信號分析的穩定性，需要根據信號的小波重構誤差確定最優小波基，從而保證信號分析的穩定性。目前，常用的判定指標有均方誤差和最大均方誤差[1617]。

2）地質資料及天線脈沖波形的掌握越多的掌握和了解信號對應的地質資料就越容易對目標反射波和多次回波出現的位置及波形能量的大小進行預判；不同的地質雷達，具有不同的天線脈沖波形，掌握天線脈沖波形的基本形式，有利于識別信號中的被測目標反射波。

3）預測反褶積等濾波方法的參數設置運用地質資料和脈沖波形判斷各時域子信號中的噪聲成分和反射波成分。針對各時域子信號選取相應的預測反褶積等濾波方法，并分別對各濾波方法中的參數進行設置。

3應用實例

在隧道質量無損檢測中，襯砌內鋼筋網和工字鋼會嚴重影響襯砌厚度檢測和背后脫空等病害的評估，因此，設計具有已知埋深和尺寸的鐵板空腔檢測實驗，運用PDBW法對該實驗檢測信號進行處理，從而驗證該法在地質雷達信號處理中的可行性。

3.1鐵板空腔檢測實驗

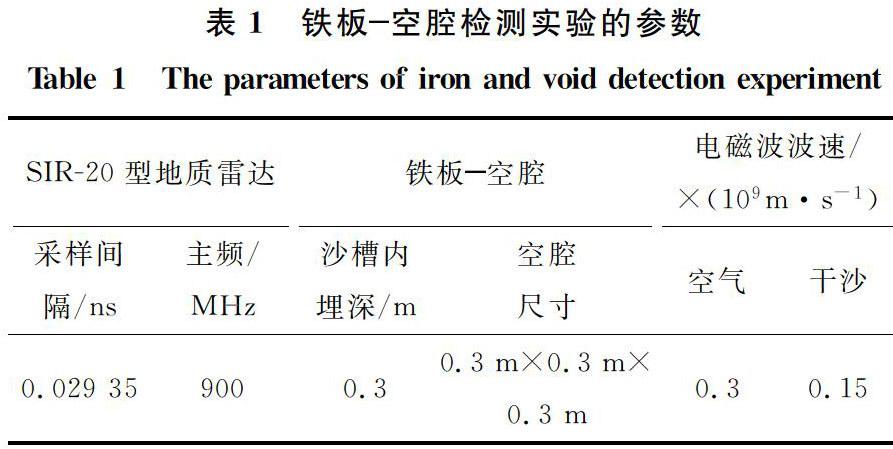
鐵板空腔檢測實驗的具體設計及模型制作過程見表1、圖2。表1鐵板空腔檢測實驗的參數

Table 1The parameters of iron and void detection experimentSIR20型地質雷達鐵板空腔電磁波波速/

×（109m·s-1）采樣間

隔/ns主頻/

MHz沙槽內

埋深/m空腔

尺寸空氣干沙0.029 359000.30.3 m×0.3 m×

0.3 m0.30.15圖2鐵板空腔檢測實驗

Fig2.The iron and void detection experiment3.2實驗檢測信號的處理及對比分析

分別采用預測反褶積法和PDBW法對鐵板空腔檢測實驗中的原始信號進行處理，通過信號的剖面圖分析和單道信號的波形分析，研究兩種方法對多次回波的抑制效果和對深部信號的識別效果。

1）原始信號的分析結果圖3（a）為鐵板空腔檢測實驗的原始信號，其中，存在明顯的沙槽表面反射波、鐵板反射波。由于薄鐵板的本征阻抗較大，電磁波產生較強的鐵板反射波和多次回波干擾，在圖3（a）的區域1中存在明顯的多次回波。根據波形分析法和倒相原理[1820]，對圖3（b）中的第30道信號進行分析，用點1、2、3確定沙槽表面反射波、鐵板反射波和多次回波的起始時間，起始時間分別為1468、5.488、8.776 ns，見表2。為了提高地質雷達探測分辨率和圖像分析的準確性，需對原始信號進行濾波處理。

圖3原始信號及其第30道信號

Fig.3The original signal and its No.30 trace2）預測反褶積法處理后信號的分析結果圖4（a）為預測反褶積法處理后的信號，可以看出，區域1中的多次回波得到有效抑制，并在區域2中出現明顯的反射波信號。圖4（b）為處理后的第30道信號，根據波形分析法和倒相原理，運用點1、2表示沙槽表面反射波、鐵板反射波的起始時間，用點3表示反射波3的起始時間，起始時間分別為1.468、5.488、8.834 ns，見表2。在表2中，預測反褶積法處理后信號中各反射波的起始時間與原始信號中各反射波的起始時間基本相等，所以，反射波3為多次回波。這表明，預測反褶積法只是對原始信號中的多次回波進行壓制，并不能識別具有低信噪比的空腔底面反射波。

圖4預測反褶積法處理后信號及其第30道信號

Fig.4The processed signal by predictive deconvolution

method and its No.30 trace3）PDBW法處理后信號的分析結果運用DB和Bior系列小波對原始信號進行重構誤差分析，選取Bior2.4小波基為PDBW法中的最優小波。圖5（a）為PDBW法處理后的信號，可以看出區域1中的多次回波得到有效抑制，并在區域2中出現明顯的反射波信號。圖5（b）為處理后第30道信號，根據波形分析法和倒相原理，運用點1、2確定沙槽表面反射波和鐵板反射波的起始時間，用點3表示反射波3的起始時間，起始時間分別為1.497、5.459、7.631 ns，見表2。在表2中，與原始信號相比，PDBW法處理后信號中的反射波1和反射波2的起時間基本不變，但反射波3的起始時間發生明顯變化，時間差值為1.145 ns。令反射波3為空腔底面反射波，并對PDBW法處理后的信號進行定量分析，得到鐵板的計算深度和空腔的計算垂直尺寸分別為0.297 m和0.326 m，與實際值相比，計算誤差為0.003 m和0.026 m，見表3。這表明PDBW法能準確識別空腔底面反射波，并能在壓制多次回波的同時提高空腔底面反射波的信噪比，從而實現提高探測分辨率和圖像分析準確性的目的。即上述分析結果驗證了PDBW法在抑制多次回波干擾、識別深部信號和提高深部信號信噪比方面的可行性。

圖5PDBW法處理后信號及其第30道信號

Fig.5The processed signal by PDBW method

and its No.30 trace表2處理后信號中反射波的起始時間

Table 2The start time of reflection waves in processed signals原始信號起始時

間/ns預測反褶積法處理后信號起始時

間/ns時間差

值/nsPDBW法處理后信號起始時

間/ns時間差

值/ns反射波11.4681.46801.4970.029反射波25.4885.48805.4590.029反射波38.7768.8340.0587.6311.145注：反射波1為信號中出現的第一道反射波信號，以此類推。

表3PDBW法處理后第30道信號的定量分析

Table 3The quantitative analysis of processed signal by PDBW實際值PDBW法處理后信號計算值誤差值深度/m0.3000.2970.003垂直尺寸/m0.3000.3260.026注：深度為實驗模型的埋深，即鐵板的埋深；垂直尺寸為實驗模型的厚度，即鐵板表面到空腔底面之間的距離。4結論

1）根據地質雷達檢測信號的固有特點，將傳統的反褶積法與小波分析相結合，提出雙正交小波預測反褶積法（PDBW法），并將PDBW法成功用于地質雷達檢測信號的分析和處理。

2）PDBW法能有效抑制多次回波干擾，與預測反褶積法相比，PDBW法能夠準確識別深部信號，提高深部信號的信噪比，從而改善地質雷達的探測分辨率和圖像分析的準確性，并進一步提高了工程結構質量的檢測效果。

3）PDBW法能有效應用于地質雷達檢測信號處理，由于地震波與雷達波均遵循波的傳播理論，并具有相同的線性褶積模型，使得PDBW法在理論上也適用于地震信號的處理，下一步將開展PDBW法對地震信號應用效果的研究與驗證。

參考文獻：

[1] BENEDETTO A，PAJEWSKI L. Civil engineering applications of ground penetrating radar [M]. Switzerland：Springer International Publishing， 2015.

[2] 曾昭發，劉四新，馮晅，等.探地雷達原理與應用[M].北京：電子工業出版社，2010.

[3] 凌同華，張勝，李升冉.地質雷達隧道超前地質預報檢測信號的HHT 分析法[J].巖石力學與工程學報，2012，31（7）：14221428.

LING T H， ZHANG S， LI S R. Hilberthuang transform method for detection signal of tunnel geological prediction using ground penetrating radar [J]. Chinese Journal of Rock Mechanics and Engineering， 2012， 31（7）： 14221428. （in Chinese）

[4] BERNATEKJAKIEL A， KONDRACKA M. Combining geomorphological mapping and near surface geophysics （GPR and ERT） to study piping systems [J]. Geomorphology， 2016， 274 （1）： 193209.

[5] PONGSAK W， RAKTIPONG S， SOMNUK T， et al. A new method to determine locations of rebars and estimate cover thickness of RC structures using GPR data [J]. Construction and Building Materials， 2017， 140 （1）： 257273.

[6] 石剛，田養軍，王亞瓊，等.基于模糊分形脈沖反褶積的探地雷達信號處理[J].長安大學學報（自然科學版），2012，32（5）：7984.

SHI G， TIAN Y J， WANG Y Q， et al. Signal processing of groundpenetrating radar on the principle of deconvolution based on fuzzy fractal pulse [J]. Journal of Changan University （Natural Science Edition）， 2012， 32 （5）： 7984. （in Chinese）

[7] 蘇茂鑫，李術才，薛翊國，等.基于反褶積的探地雷達高分辨率處理方法[J].浙江大學學報（工學版），2010，44（6）：12011206.

SU M X， LI S C， XUE Y G. Ground penetrating radars high resolution processing method based on deconvolution [J]. Journal of Zhejiang University （Engineering Science）， 2010， 44 （6）： 12011206. （in Chinese）

[8] ECONOMOU N， VAFIDIS A. GPR data time varying deconvolution by kurtosis maximization [J]. Journal of Applied Geophysics， 2012（81）： 117121.

[9] 王萬里，楊午陽，魏新建，等.隨機稀疏脈沖非線性反褶積[J].地球物理學進展，2014，29（4）：17801784.

WANG W L， YANG W Y， WEI X J， et al. Stochastic sparse spike nonlinear deconvolution [J]. Progress in Geophysics， 2014， 29（4）： 17801784. （in Chinese）

[10] CHANG Y F， MA Y， LIN C M， et al. Reverberation reduction in ultrasonic images via predictive deconvolution [J]. NDT & E International， 2008， 41（4）： 235241.

[11] TZANIS A. Detection and extraction of orientationandscaledependent information from twodimensional GPR data with tuneable directional wavelet filters [J]. Journal of Applied Geophysics， 2013， 89：4867.

[12] NGUYEN S T， BRIAN W H. Biorthogonal rational discrete wavelet transform with multiple regularity orders and application experiments [J]. Signal Processing， 2013， 93（11）： 30143026.

[13] MOURAD K， FETHI B R. Efficient automatic detection of QRS complexes in ECG signal based on reverse biorthogonal wavelet decomposition and nonlinear filtering [J]. Measurement， 2016， 94： 663670.

[14] MACEDO I A S， SILVA C B， FIGUEIREDO J J S. Comparison between deterministic and statistical wavelet estimation methods through predictive deconvolution： Seismic to well tie example from the North Sea [J]. Journal of Applied Geophysics， 2017， 136： 298314.

[15] FLETCHER P， SANGWINE S J. The development of the quaternion wavelet transform [J]. Singal Procsessing， 2017， 136： 215.

[16] 成謝鋒，張正.一種雙正交心音小波的構造方法[J].物理學報，2013，62（16）：168701.

CHENG X F， ZHANG Z. A construction method of biorthogonal heart sound wavelet [J]. Acta Physica Sinica，2013， 62（16）： 168701. （in Chinese）

[17] HACHICHA W， KAANICHE M， BEGHDADI A， et al. Noreference stereo image quality assessment based on joint wavelet decomposition and statistical models [J]. Signal Processing： Image Communication， 2017， 54： 107117.

[18] FENG X， LIANG W J， LIU C， et al. Application of Freeman decomposition to full polarimetric GPR for improving subsurface target classification [J]. Signal Processing， 2016， 132： 35343537.

[19] 楊艷青，賀少輝，齊法琳，等.鐵路隧道襯砌地質雷達非接觸檢測模擬試驗研究[J].巖石力學與工程學報，2011，30（9）：1761–1771.

YANG Y Q， HE S H， QI F L， et al. Simulation test of GPR noncontact detection on lining of railway tunnel [J]. Chinese Journal of Rock Mechanics and Engineering，2011，30（9）：1761–1771. （in Chinese）

[20] 胡進峰，周正歐.淺地層探地雷達目標探測和定位新方法[J].儀器儀表學報，2006，27（4）：371375.

HU J F， ZHOU Z O. Target detection and orientation in sursurface penetrating radar data [J]. Chinese Journal of Scientific Instrument， 2006， 27（4）：371375. （in Chinese）