“簡單的線性規劃問題”的八步教學設計

崔靜靜

【摘要】數學技能指學生在學習數學知識的過程中，通過訓練完成數學學習任務的一種行動或心智行動方式.數學技能分為動作技能和心智技能.基于促進數學技能習得的相關理論，對簡單的線性規劃問題進行“八步”教學設計：“設”—“列”—“畫”—“化”—“移”—“看”—“求”—“悟”，并說明各步的設計意圖.這樣設計有利于突出重點，突破難點.代數法、向量法也可作為一般方法解此類問題.

【關鍵詞】技能習得；線性規劃；“八步”教學設計

2017年9月22日至24日，全國第二屆全日制教育碩士學科教學（數學）專業教學技能大賽（決賽）在山東煙臺魯東大學舉行，本次大賽共涉及高中數學的8個課題，“簡單的線性規劃問題”是其中一個，該課題選自人教社普通高中課程標準試驗教科書數學5（必修）（A版）[1].筆者在賽后寫下了“簡單的線性規劃問題”的教學設計.

1數學技能的相關理論的簡述

數學技能指學生在學習數學知識的過程中，通過訓練完成數學學習任務的一種行動或心智行動方式.數學技能可分為動作技能和心智技能[2].

動作技能指數學活動中由一系列實際操作以合理、完善的程序構成的操作活動方式.它具有外顯性、客觀性、非簡約性三個基本特點.

心智技能是指借助內部言語在大腦中按合理完善的方式自動地進行數學認知活動方式，它是經過后天的學習和訓練而形成的.它具有以下特點：（1）心智技能的作用對象是抽象的數學概念、命題與表象；（2）心智技能的動作是借助內部言語在頭腦內部完成的，其他人很難從外部觀測到學習主體的變化情況；（3）簡縮性，即動作成分可以省略、合并、簡化；（4）有時需要借助動作技能加以完成；（5）依附于一定的數學概念、法則，建立在理解的基礎之上；（6）可通過練習提高技能實施的速度與效率.

中小學課程中的數學基本技能包括：數值運算技能、符號操作技能、圖形處理技能、數據分析技能、推理論證技能、數學交流技能等.

2促進數學技能習得的教學設計

2.1教材分析

2.1.1教學內容分析

“簡單的線性規劃問題”是人教社A版普通高中課程標準試驗教科書數學5（必修）第三章《不等式》中第3節的第二個內容.該課題是在學習了不等式的性質和“二元一次不等式（組）與平面區域”之后的一個教學內容.因此，“簡單的線性規劃問題”可看成是“不等式的性質”和“二元一次不等式（組）與平面區域”的應用.顯然，解決“簡單的線性規劃問題”也必需“直線的方程”等解析幾何知識作基礎.

2.1.2教學目標分析

通過教學，能讓學生從工廠產品的實際問題中建立起數學模型，在教師啟發和引導下，學生能利用學過的知識和方法解決這個數學模型，并由此建構線性規劃問題、目標函數、可行解、可行域、最優解等系列概念.掌握求解線性規劃問題的最優解的方法和一般步驟.

2.1.3教學問題診斷分析

線性規劃問題的求解，需要學生具備一定的數學心智技能和動作技能才能完成.線性規劃的教學，學生在最優解的求解過程中容易出現“似懂非懂”、“懂而不會”和“眼高手低”的情況.因此，教師可著眼于數學技能的相關理論及應用，而著手于“八步”教學設計即“設”—“列”—“畫”—“化”—“移”—“看”—“求”—

“悟”.這既有利于學生外化于形的動作技能的練成，又有利于學生內化于心的心智技能的形成，從而，真正使學生的數學心智技能和動作技能得到有效訓練，真正使學生經歷求解線性規劃最優解的一般步驟，并掌握其方法、體會其思想.

2.2簡單的線性規劃問題的“八步”教學設計與簡略說明

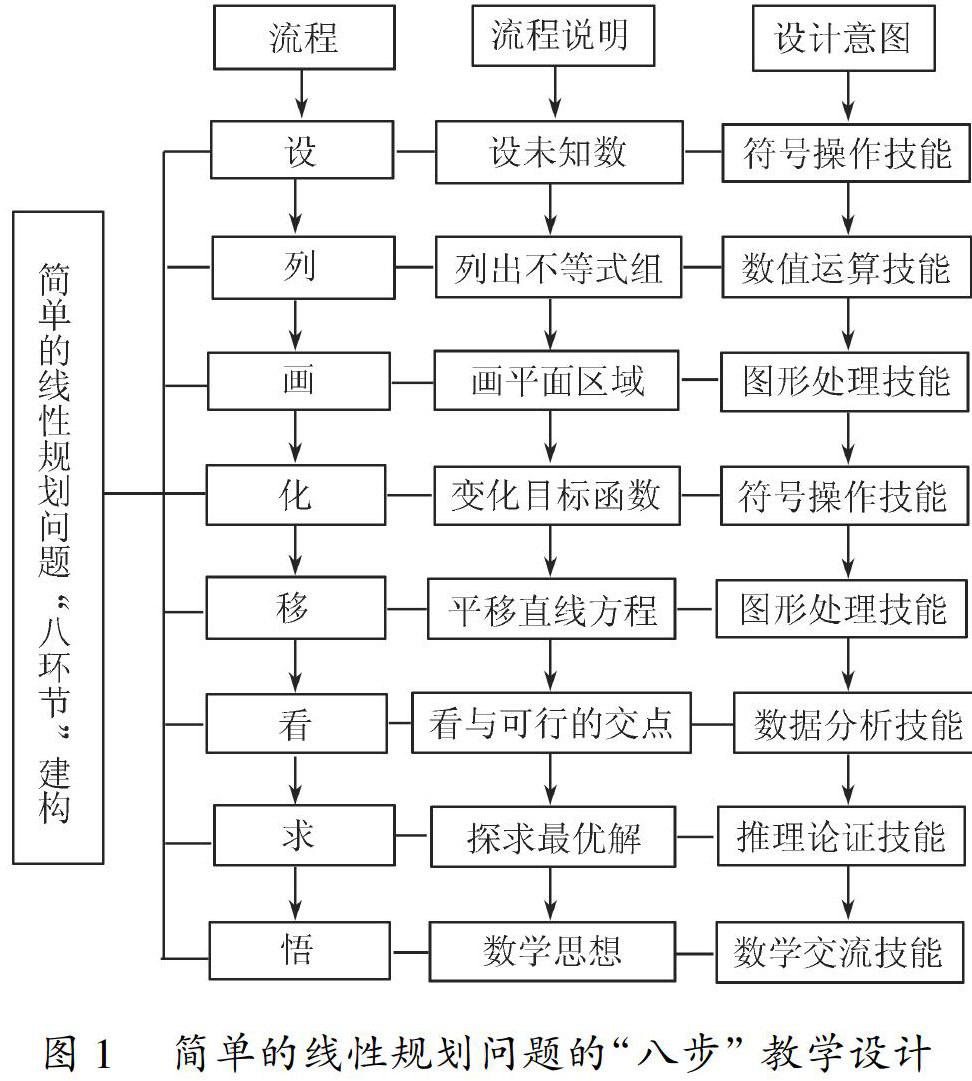
基于技能習得理論下簡單線性規劃問題的“八步”教學設計（或稱“八環節”）的流程圖，如圖1.圖1簡單的線性規劃問題的“八步”教學設計2.2簡單的線性規劃問題“八步”教學的實施建議與設計意圖分析

依據促進數學技能習得的相關理論制定“八步”教學設計，提出了如下實施建議，并對每一步說明設計意圖.

第一步：“設”

學生學習本節之前已經學習了一元二次不等式及其解法，能夠根據題意列出二元一次不等式組并畫出其表示的平面區域.

教學設計：某工廠用A、B兩種配件生產甲、乙兩種產品，每生產一件甲產品使用4個A配件耗時1h，每生產一件乙產品使用4個B配件耗時2h，該廠每天最多可從配件廠獲得16個A配件和12個B配件，按每天工作8h計算，該廠所有可能的日生產安排是什么？

問題1若生產一件甲產品獲利2萬元，生產一件乙產品獲利3萬元，采用哪種生產安排利潤最大？

依據題意，將重要信息提取到表格中，如圖1.

AB時間（小時）獲利甲/件412萬元乙/件423萬元日生產（限制）16128圖1

此時，設x 、y件，利潤為z 萬元.

【設計意圖】“設”是指依據題意設出未知元，用字母代替數，變元x、y代替未知量甲、乙兩種產品的生產量.把實際問題轉化為線性規劃模型，提高學生分析問題、解決問題的能力[3].用代數方法進行解決，培養了學生的符號操作技能.

第二步：“列”

由上，化簡后列出二元一次不等式組、求利潤的表達式.

教學設計：要求學生獨立完成該步.

x+2y≤8，

x≤4，

y≤3，

x≥0，

y≥0.（1）

z=2x+3y.

列出上面的式子后，教師應趁機引導學生形成、理解相關概念.

1.不等式組（1）x+2y≤8，

x≤4，

y≤3，

x≥0，

y≥0.是對變量x、y的約束條件，這組約束條件是關于x、y的一次不等式，所以又稱為線性約束條件.

2.求最大值的函數z=2x+3y叫做目標函數，且它是關于變量x、y的一次解析式，所以又叫做線性目標函數.

3.在線性約束條件下求線性目標函數的最大值或最小值問題，統稱為線性規劃問題.

4.滿足線性約束條件的解（x，y）叫做可行解.由所有可行解組成的集合叫做可行域.

5.使目標函數取得最大值或最小值的可行解叫做這個問題的最優解.

【設計意圖】考察學生根據實際需要合理的選擇適當的工具和方法，列出并化簡已知條件給定的二元一次不等式組，培養了學生的數值運算技能.這里對教材的安排作了略微的調整.先對概念進行解讀，再探求最優解，符合學生的認知規律.

第三步：“畫”

圖2教學設計：讓學生自己畫出二元一次不等式組表示的平面區域，如圖2，并結合圖象解讀以上概念，使學生加深對概念的理解.

【設計意圖】要求學生準確地畫出上面二元一次不等式組表示的平面區域.作圖是學習數學知識、解決數學問題的重要手段，有助于培養學生的圖形處理技能.

第四步：“化”

將目標函數z=2x+3y畫在平面區域上是探求最優解的突破口.

教學設計：教師引導學生把目標函數z=2x+3y變形為y=-23x+z3，這是斜率為-23，縱截距為z3的直線.

圖3【設計意圖】數學抽象的最終結果是符號化，包括了符號演算能力、表達式的變形和等價轉化能力、數形結合能力、圖像符號能力等.引導學生化目標函數為直線方程的形式.要求學生熟練地進行字母式的演算和變形，將目標函數z=2x+3y變形為y=-23x+z3再加以討論，培養學生的符號操作技能.

第五步：“移”

當利潤z從0開始變化時，可以得到一組互相平行的直線，如圖3.

【設計意圖】平移直線方程y=-23x+z3，為下一步“看”建立了直觀形象的思維支柱.

第六步：“看”

看直線y=-23x+z3與可行域有公共點時，在可行域內找一點M，使直線經過點M時縱截距z3最大.

教師借助幾何畫板演示直線y=-23x+z3在可行域內平移.

設計意圖：“看”是指看直線方程與可行域的交點，意圖培養學生的數據分析能力.

第七步：“求”

由上，可知當直線y=-23x+z3經過直線x=4與直線x+2y-8=0的交點M（4，2）時，縱截距z3最大.

此時利潤最大值zmax=2×4+3×2=14.

設計意圖：依據題意求縱截距的最大值或最小值.

第八步：“悟”

感悟線性規劃問題中蘊含的思想方法，形成求解此類題型的一般方法.

【設計意圖】讓學生對整個解決過程中蘊含的思想方法進行總結歸納，形成個人知識、思想方法，讓其享受做數學的樂趣.

3解決線性規劃問題的其他兩種方法

以上的教學設計是解決線性規劃問題的常用幾何法，下面再給出兩種一般方法.

代數法

步驟一：將不等式變為方程，兩兩聯立后求其解（x1，y1），（x2，y2），…，（xn，yn）.步驟二：將所有解帶入目標函數，得到目標函數值z1，z2，…zn.步驟三：檢驗.即若z1為所求的最大值，則將（x1，y1）代到線性可行域的不等式驗證，若全部符合，則z1為最值.

向量法

對于目標函數z=2x+3y，可構造a=（2，3），b=（x，y），則z=a·b.

因為a·b=a·b·cos，

所以z=22+32·b·cos=13·b·cos.

按照向量的幾何意義，b·cos表示b在a上的投影，即當b在a上的投影最大值，z取最大值.由圖3可知，當b=（4，2）時，z取最大值a·b=（2，3）·（4，2）=14.

4結語

將簡單線性規劃問題的八步教學設計歸結為幾何法，其中每一步對學生應該掌握的技能都做了相應的要求，其中“畫”、“移”等是動作技能，“設”、“化”等是心智技能.當然也不能孤立地看待某個過程為動作技能或心智技能，更多的是兩者的結合，教學的目的也即是實現二者的完美結合，培養出對社會有價值的實用型人才.

參考文獻

[1]劉紹學，錢珮玲等. 普通高中課程標準實驗教科書數學5（必修）（A版） [M]. 北京：人民教育出版社，2007：12.

[2]鮑建生，周超.數學學習的心理基礎與過程[M].上海：上海教育出版社，2009.10：151.

[3]耿永雪，張吉.簡單的線性規劃問題的教學思考[J].數學通訊，2002（3）：20.