某轎車前懸架系統參數設計與仿真分析

薛玉斌，沈子鑒，李剛

（1.錦州萬得汽車技術有限公司，遼寧 錦州 121007；2.遼寧工業大學汽車與交通工程學院，遼寧 錦州 121001）

前言

汽車平順性也稱為汽車舒適性，是汽車重要性能之一[1]。對于轎車而言，客觀上要求具有良好的平順性，而懸架系統設計直接影響轎車的平順性的好壞，如何對轎車懸架系統參數進行合理設計，同時縮短開發周期，是轎車開發中的一個重要課題。文獻[2-5]給出了懸架系統和彈性部件設計方法，但是對于參數最終選取合理性沒有給出仿真實驗驗證方法。論文以某轎車為例，進行前懸架系統參數設計，并通過仿真手段對重要參數選取合理性進行驗證。

1 懸架剛度和撓度計算

整車軸距為 2300mm，前輪輪距 1215mm，滿載時前軸荷為530kg，后軸荷為490kg。前懸架非簧載質量約占簧載質量的1/6。設前懸架簧載質量為m1，計算得到m1為454kg。

1.1 剛度計算

汽車前懸架與其簧載質量組成的振動系統的固有頻率，是影響汽車行駛平順性的主要參數之一。懸架自振頻率選取的主要依據是ISO2631《人體承受全身振動的評價指南》。乘用車前懸架滿載固有頻率要求在 1.00―1.45Hz，一般在0.80―1.15Hz[2-3]。設該轎車前懸架固有頻率為n1，選取為1.1Hz。汽車前懸架固有頻率n1可用下式表示：

式中，c1為前懸架的剛度（N/m）；m1為前懸架簧上質量。將m1代入上式，得：

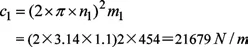
單邊剛度為10839.5。

1.2 靜撓度與動撓度計算

1.2.1 靜撓度計算

懸架的靜撓度是指汽車滿載靜止時懸架上的載荷與此時的懸架的剛度之比。懸架的靜撓度直接影響車身振動的頻率，必須正確選取懸架的靜撓度保證汽車平順性。當采用彈性特性為線性變化的懸架時，計算前懸架的靜撓度：

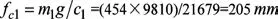
式中：g為重力加速度，取9810mm/s2。

1.2.2 動撓度計算

懸架的動撓度是指懸架從滿載靜平衡位置開始壓縮到結構允許的最大變形時，車輪中心相對于車架（或車身）的垂直位移。為了防止在不平路面上行駛時經常沖擊緩沖塊，懸架還必須具備足夠大的動撓度，轎車靜、動撓度取值范圍為分別為 100mm～300mm、70mm～90mm，動撓度與靜撓度之比一般大于0.5。設前懸架動撓度為fd1，則= 102.5mm，取fd1=103mm。

2 減振器性能參數計算

2.1 減振器相對阻尼系數

相對阻尼系數的物理意義是減振器的阻尼作用在與不同剛度c和不同簧上質量ms的懸架系統匹配時，會產生不同的阻尼效果。ψ值大，振動能迅速衰減，同時又能將較大的路面沖擊傳到車身；ψ值小則反之。通常情況下，將壓縮行程時的相對阻尼系數ψY取得小些，伸張行程的相對阻尼系數ψS取得大些。兩者之間保持ψY=(0.25～0.50)ψS的關系。

設計時，先選取ψY與ψS的平均值ψ。對于無內摩擦的彈性元件懸架，取ψ=0.25～0.35；對于有內摩擦的彈性元件懸架，ψ值取小些。對于行使路面條件較差的汽車，ψ值應取大些，一般取ψS＞0.3；為避免懸架碰撞車架，取ψY=0.50ψS[2-3]。

該轎車為微型轎車選取：前懸架相對阻尼系數ψ前=0.3，則伸張行程時的相對阻尼系數ψS=0.4，壓縮行程時的相對阻尼系數ψY=0.2[2-3]。

2.2 減振器阻尼系數δ的確定

減振器阻尼系數則前懸架阻尼系數δf。

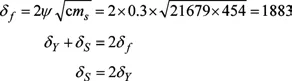
由此可得伸張阻尼系數δs=2510Ns/m，壓縮阻尼系數δY=1255Ns/m。

3 振動系統建模與仿真分析

汽車在一定路面上行駛時，其振動量（振幅、振動速度及加速度）的大小取決于汽車的質量、懸架剛度、阻尼等結構參數。論文建立 1/4汽車振動系統模型，應用Matlba/Simulink建立仿真模型，對設計的參數進行仿真分析。

建立二自由度汽車振動系統動力學模型[6]如圖1所示。

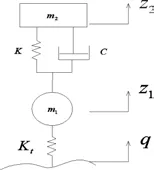
圖1 汽車振動系統模型

圖中參數意義：Z1為非簧載質量垂直位移；Z2為簧載質量（車身質量）垂直位移；q為路面不平度；K為懸架剛度；Kt為輪胎剛度；C為減振器阻尼系數。

將車輛兩自由度振動模型動力學方程寫成矩陣形式：

即：

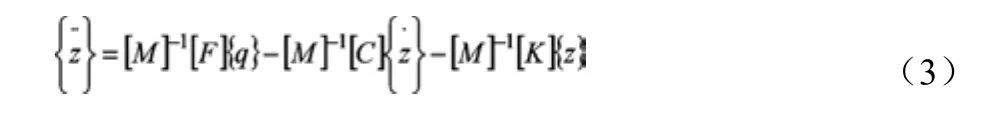
對式子（2）進行求解：

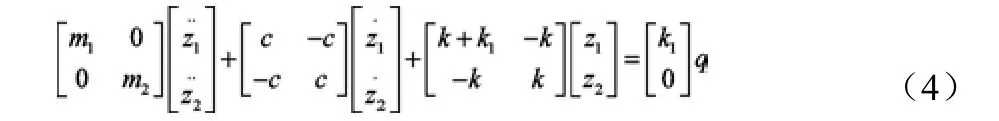
按這種方法對（3）進行求解，即可得到公式（4）求出簧載質量和非簧載質量的垂直加速度。

路面不平度即路面譜可通過基于濾波白噪聲法建立路面隨機激勵時域進行描述：

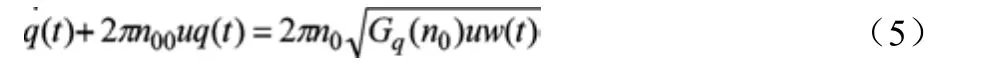
u是縱向車速，（B級路面）是參考空間頻率n0=0.1m-1下路面功率譜密度值，n00=0.01m-1是路面空間截止頻率。

懸架動撓度：

車輪動載荷：

車輪相對動載荷：

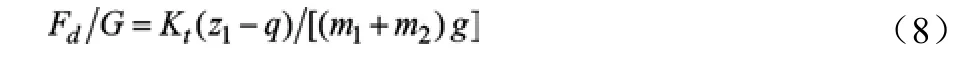
根據前面公式（2）～（8），應用Matlab/simulink[7]建立的車輛振動兩自由度動力學模型，如圖2所示。仿真工況B級路面，車速70km/h，仿真曲線如圖3到圖6所示。

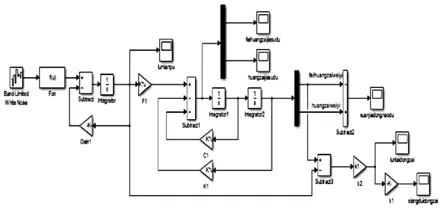
圖2 車輛振動兩自由度動力學Matlab/Simulink模型

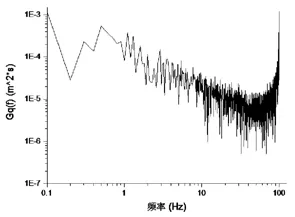
圖3 路面譜功率譜密度曲線

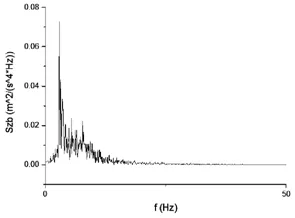
圖4 車身垂直加速度功率譜密度

如圖3-圖6為路面功率譜密度、車身垂直加速度、懸架動撓度、車輪相對動載荷功率譜密度仿真曲線。如圖 4、5所示，可以看到所設計的前懸架剛度和阻尼匹配后車身振動固有頻率為1.1Hz，懸架動撓度對應固有頻率為1.2Hz，二者峰值較小，懸架系統能保證車輛振動過程中避免懸架限位塊對車架撞擊，圖6所示的車輪相對動載曲線峰值較小，說明在較高速行駛時汽車具有良好安全性，設計出的懸架剛度和阻尼參數滿足平順性要求。

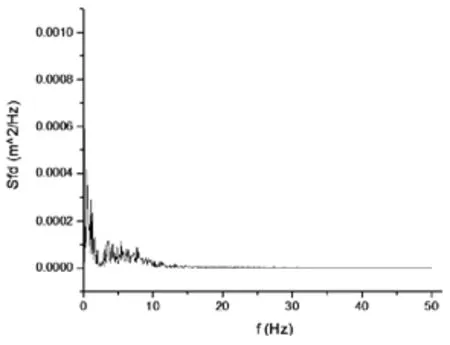
圖5 懸架動撓度功率譜密度曲線

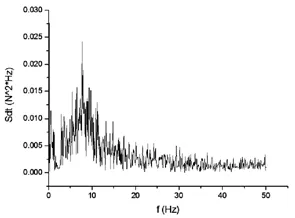
圖6 相對車輪動載功率譜密度曲線

4 結論

（1）論文給出了對轎車懸架系統主要參數設計計算和通過仿真手段對參數合理性進行驗證的方法。

（2）論文研究方法對于實際轎車懸架系統開發、提高開發效率方面具有一定參考價值。

參考文獻

[1] 喻凡,林逸.汽車系統動力學[M].北京:機械工業出版社,2005 .

[2] 劉惟信.汽車設計[M].北京:清華大學出版社,2010.

[3] 王望舒.汽車設計第4版[M].北京:機械工業出版社,2004:209-210.

[4] 曾慶東.汽車減振器設計[M].機械工業出版社,1999.

[5] 史小輝.汽車懸架彈簧現代設計方法研究[M]. 西南交通大學出版社,2011.

[6] 余志生.汽車理論第5版[M].北京:機械工業出版社,2014.

[7] 李獻,駱志偉,于晉臣. MATLAB/Simulink 系統仿真[M].北京:清華大學出版社,2017.