無線可充電傳感器網絡中充電器的部署優化
王志方,鄭 霖,李曉記
(1.桂林電子科技大學 信息與通信學院,廣西 桂林 541004; 2.廣西信息科學實驗中心,廣西 桂林 541004)
0 概述
無線傳感器網絡(Wireless Sensor Network,WSN)由部署在監測區域內的大量傳感器節點和一些匯聚節點組成,是通過無線通信方式形成的多跳自組織網絡系統。在WSN中,傳感器節點協作地感知、采集和處理網絡覆蓋區域中被感知對象的信息,并發送給觀察者[1-2],其中傳感器節點由有限的一次性電池供電且很難更換電池[3],這使得WSN的生命周期受到影響,嚴重制約其發展。文獻[4]在實驗中采用磁諧振耦合的技術驗證了無線能量傳輸的可行性,這為WSN中傳感器節點的能量補充提供了一個解決方案。
由無線充電器充電的無線傳感器網絡也稱為無線可充電傳感器網絡(Wireless Rechargeable Sensor Network,WRSN)[5-6]。WRSN中一個關鍵問題是無線充電器的部署問題。無線充電器很昂貴[7],并且它們的部署需要花費很多的時間和成本,如何有效地部署無線充電器,使得網絡的充電代價最小化,是一個亟待解決的問題。
目前針對WRSN的研究多數為對移動充電策略的研究[8-9],而對固定天線充電器部署問題的研究并不多見。文獻[10]研究在室內的環境下如何部署配有定向天線的無線充電器,使得無線充電器覆蓋全部傳感器節點,并提出了基于節點的貪心錐選擇算法和基于對的貪心錐選擇算法。文獻[11]提出一種基于自適應對的貪心錐選擇(APB-GCS)算法,通過迭代以貪婪地選擇覆蓋大多數傳感器的充電器。文獻[12]中假設充電器網絡的布置為等邊三角形,通過研究點配置和路徑配置這兩種形式,使用最少數量的充電器來確保放置在網絡任何位置的靜止或移動的標簽可以獲得足夠的功率用于持續正常工作。文獻[13]考慮數據匯點對傳感器的影響,提出一種能夠減少所需定向充電器數量并仍然保持良好充電效果的功率平衡感知部署方法。
上述針對無線充電器部署的研究忽略了節點的位置關系和拓撲特征,傳感器節點隨機地分布在指定區域中,會造成傳感器節點的密度不均勻,使得充電器的數目增多。為此,本文定義室內隨機非均勻環境下WSN的充電覆蓋問題,尋找最少數量的固定無線充電器,其中充電器位于網格頂點處,且充電器的覆蓋區域被假設為圓形。為部署傳感器節點非均勻分布下最少數目的充電器,根據文獻[14-15]的啟發,將節點的位置關系和拓撲特征考慮到充電器的選擇中,提出利用分割技術和移位策略的近似算法,并結合最小包圍圓算法,設計基于k-中心點算法的聚類分區算法。
1 WSN網絡模型和問題
如圖1所示,給定一個無線可充電傳感器網絡,其中傳感器節點隨機的部署在長為L、寬為W的長方形區域內,負責為傳感器節點進行充電的充電器位于距離長方形H的高度處。如圖2所示,無線充電器配備有3D波束成形定向天線。當傳感器節點位于無線充電器的充電圓錐內,即傳感器節點位于無線充電器的覆蓋范圍內,假定傳感器節點可以接收到無線充電器傳輸的能量。

圖1 無線可充電傳感器網絡示意圖

圖2 無線充電器覆蓋模型
充電范圍R是指在無線充電器的范圍內使得在傳感器節點的功率接收率至少超過一個閾值δ,這里傳感器節點i的功率接收率用Ui表示。Ui是與距離有關的參數,隨著節點i與無線充電器的距離增大而減小,當傳感器節點i與無線充電器的距離大于r0,此處假定其功率接收率過低,使得傳感器節點的電池磁諧振耦合無法正常工作。rij為傳感器節點i到無線充電器j的距離,當rij≤r0時,節點i的功率接收率Ui=μ(rij)×UFull,否則Ui=0。這里UFull是無線充電汽車(Wireless Charging Vehicle,WCV)為單個傳感器節點滿功率輸出,μ(rij)為無線功率傳輸的效率,μ(rij)是關于rij的減函數,且0≤μ(rij)≤1。本文旨在使用最少數量的無線充電器對平面中的所有傳感器節點進行充電,該問題定義如下:
問題1給定位于歐幾里得平面U的目標傳感器節點,尋找到最少數目的充電器,使得充電器能覆蓋全部的傳感器節點,并且每個傳感器節點至少被無線充電器覆蓋一次。
2 算法設計


圖3 無線充電器充電范圍

2.1 近似算法
假設Q是覆蓋N中所有點的正方形。用于問題1的分割技術的思想如下:首先將正方形Q劃分為稱為單元的正方形網格,每個大小為m×m,其中m為常數(見圖4);然后解決每個單元的問題1;最后將所有單元的解的聯合作為對原始輸入的解[16]。
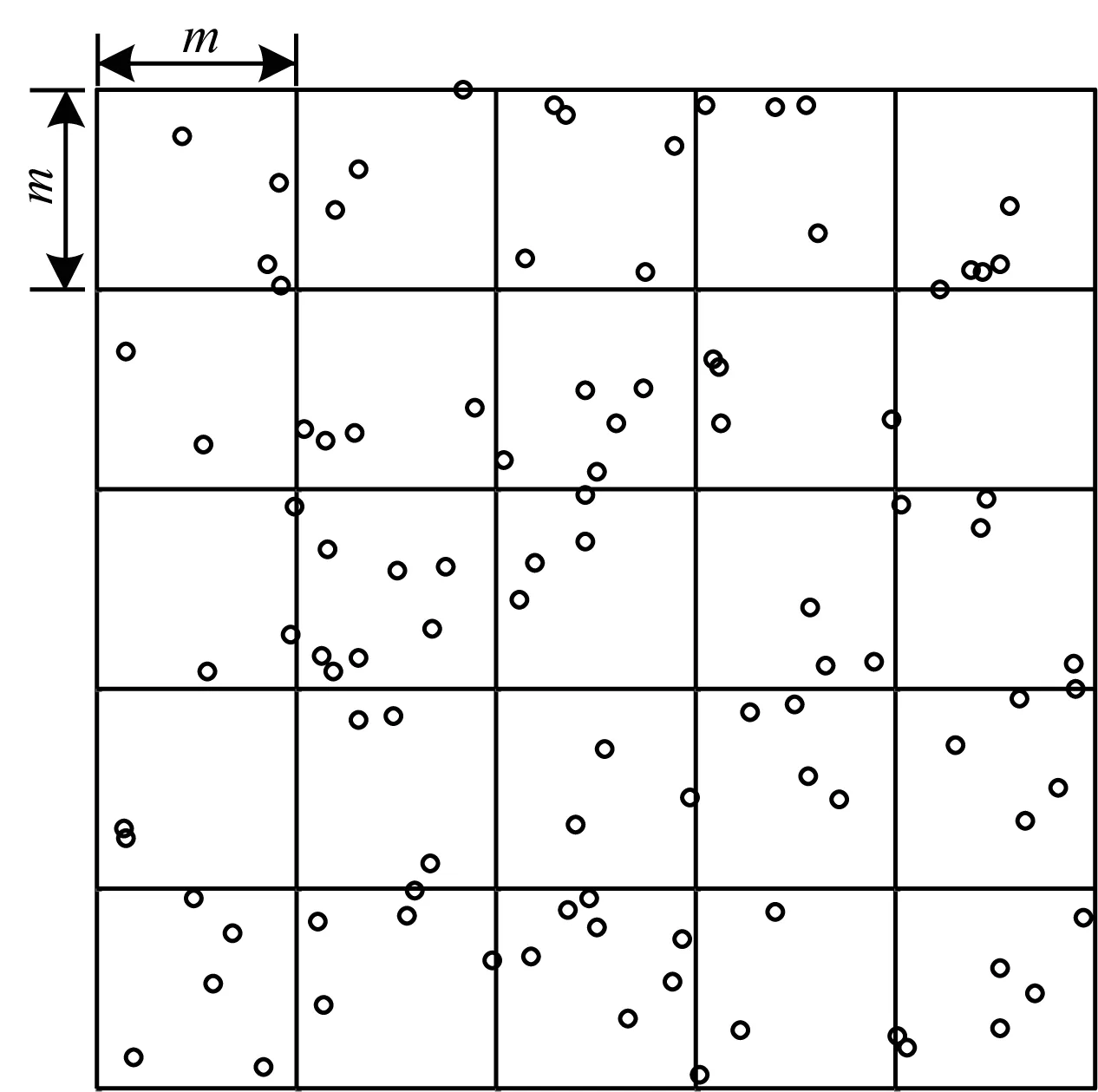
圖4 m×m正方形網格
近似算法的具體步驟如下:
步驟1將平面U劃分成正方形,邊長皆為m(m>2d0),集合Q=F1∪F2∪…∪Fu,其中Fi表示有節點存在的正方形,u為節點存在的正方形的數目。
步驟2對任一集合Fi,尋找單元格中最少數目的充電器Fi(c)。
步驟3輸出Q=∪Fi(c)。
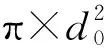
因此,在所有非空單元格中,算法總時間為:
(1)
所有目標傳感器節點隨機分布在平面U上。本文通過移位策略,移動單元格以減少充電器的數目。


圖5 移位策略示意圖
下面對近似算法的近似比進行分析。每個單元格為m×m的正方形,這里假設單元格不包括上、右側邊界。假定Di為劃分P(i,i)中所有單元格的最少數目充電器的并集。將劃分P(i,i)中位于水平或垂直格線的所有單元格的集合成為P(i,i)的一個條塊。用Hi和Vi分別表示D*中與P(i,i)的水平和垂直條塊相交的所有單元格的集合。如果充電器與多個單元格相交,則它必須屬于Hi或者Vi,且每個充電器最多與4個單元格相交,因此,有:
|Di|≤|D*|+|Hi|+2|Vi|
(2)
當a≠b時,一個充電器不可能既屬于Va又屬于Vb,即所有的集合Va,a=0,1,…,m-1都是兩兩不相交的。因此,有:
(3)
同理可得:
(4)

2.2 聚類分區算法
初始化移動位置集合M=?,聚類分區算法的具體步驟如下:
步驟1令k=1,S=?。
步驟2使用k-中心點算法進行分類并計算出每一類中點的最小包圍圓[17]。
步驟3判斷是否存在半徑ri≤d0,i∈{1,2,…,k}的最小包圍圓。若存在,則將這些聚類儲存到集合S中,并且M=M∪S,然后從節點集N中去除類中的點,即N=N-S,判斷集合S是否為空集,不滿足轉到步驟1,滿足轉到步驟4;若不存在,k=k+1,轉到步驟3。
步驟4輸出集合M。
已知k-中心點算法時間復雜度為O(k(n-k)2),而最小包圍圓算法時間復雜度是線性的。假設第1次出現半徑ri≤d0,i∈{1,2,…,k}的最小包圍圓時k-中心點算法運行了k1次,此時最小包圍圓內的節點數為n1,則運行總時間為:
O((n- 1)2+2·(n-2)2+…+k1·(n-k1)2)=
(5)
假設第2次出現半徑ri≤d0,i∈{1,2,…,k}的最小包圍圓時k-中心點算法運行了k2次,此時最小包圍圓內的節點數為n2,則運行總時間為:
O((n-n1-1)2+2·(n-n1-2)2+…+
(6)

3 仿真與分析
本節展示了2種算法的仿真結果。仿真器以MATLAB和LINGO實現,仿真設置如表1所示。假設傳感器節點隨機部署在20 m×20 m平面中,其中距離平面2.82 m處的一組網格點間隔為1.414 m,以部署無線充電器。無線充電器的有效充電距離為3 m,即傳感器節點與充電器的距離在這個范圍內可以有效地補充電量,否則傳感器節點的充電效率為0。

表1 仿真設置
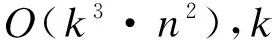
圖6和圖7分別展示了當平面上隨機部署傳感器節點的數量為100時,2種算法得到的無線充電器的數量。其中,通過近似算法計算得到的充電器的數目為36個,而通過聚類分區算法計算得到的充電器的數目為35個。由于近似算法在移位策略中,處于左邊界和上邊界的點在移位之后將不再參與分區,因此會使計算出的充電器的數目上有一定的偏差。

圖6 近似算法仿真結果

圖7 聚類分區算法仿真結果
圖8給出了近似算法、聚類分區算法和APB-GCS算法在選擇充電器數量方面的比較結果。可以看出,由近似算法和聚類分區算法求得的充電器的數目比APB-GCS算法少得多,而近似算法與聚類分區算法相差不大。
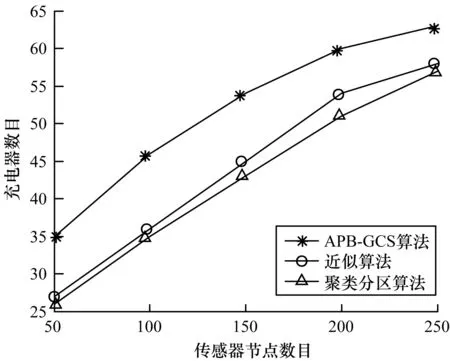
圖8 本文算法與APB-GCS算法的充電器數目比較
4 結束語
本文定義無線可充電傳感器網絡中的充電覆蓋問題,同時考慮傳感器節點隨機非均勻分布的特點,提出2種算法:將網絡劃分成網格的形式進行求解并利用移位策略減少充電器數目的近似算法,以及基于貪心算法思想的聚類分區算法。時間復雜度分析及仿真結果表明,聚類分區算法在減少充電器的數量方面性能更好,而且具有較低的時間復雜度。下一步將對充電器為傳感器節點充電的時間以及WRSN中拓撲路由對充電的影響等問題進行研究。
[1] AKYILDIZ I F,SU W,SANKARASUBRAMANIAM Y,et al.Wireless sensor networks:a survey[J].Computer Networks,2002,38(4):393-422.
[2] RAULT T,BOUABDALLAH A,CHALLAL Y.Energy efficiency in wireless sensor networks:a top-down survey[J].Computer Networks,2014,67(8):104-122.
[3] RAJBA S,RAIF P,RAJBA T,et al.Wireless sensor networks in application to patients health monitoring[C]//Proceedings of IEEE Symposium on Computational Intelligence in Healthcare and E-health.Washington D.C.,USA:IEEE Computer Society,2013:94-98.
[4] KURS A,KARALIS A,MOFFATT R,et al.Wireless power transfer via strongly coupled magnetic resonances[J].Science,2007,317(5834):83-86.
[5] DAI H P,WU X B,XU L J,et al.Practical scheduling for stochastic event capture in wireless rechargeable sensor networks[C]//Proceedings of WCNC’13.Washington D.C.,USA:IEEE Computer Society,2013:986-991.
[6] DAI H P,XU L J,WU X B,et al.Impact of mobility on energy provisioning in wireless rechargeable sensor networks[C]//Proceedings of WCNC’13.Washington D.C.,USA:IEEE Computer Society,2013:962-967.
[7] 戴海鵬,陳貴海,徐力杰,等.一種高效有向無線充電器的布置算法[J].軟件學報,2015,26(7):1711-1729.
[8] 胡 誠,汪 蕓,王 輝.無線可充電傳感器網絡中充電規劃研究進展[J].軟件學報,2016,27(1):72-95.
[9] 劉 創,王 珺,吳 涵.無線可充電傳感器網絡的移動充電問題研究[J].計算機技術與發展,2016,26(3):162-167.
[10] LIAO J H,JIANG J R.Wireless charger deployment optimization for wireless rechargeable sensor networks[C]//Proceedings of International Conference on Ubi-Media Computing and Workshops.Washington D.C.,USA:IEEE Press,2014:160-164.
[11] LIAO J H,HONG C M,JIANG J R.An adaptive algorithm for charger deployment optimization in wireless rechargeable sensor networks[J].Frontiers in Artificial Intelligence and Applications,2015,274:2080-2089.
[12] HE S B,CHEN J M,JIANG F C,et al.Energy provisioning in wireless rechargeable sensor networks[C]//Proceedings of INFOCOM’11.Washington D.C.,USA:IEEE Computer Society,2011:2006-2014.
[13] LIN T L,LI S L,CHANG H Y.A power balance aware wireless charger deployment method for complete coverage in wireless rechargeable sensor networks[J].Energies,2016,9(9):695-708.
[14] PANG Y,LU Z,PAN M,et al.Charging coverage for energy replenishment in wireless sensor networks[J].IEEE International Conference on Networking,2014,43(3):251-254.
[15] 王繼強.集合覆蓋問題的模型與算法[J].計算機工程與應用,2013,49(17):15-17.
[16] DU D Z,KO K I,HU X.Design and analysis of approximation algorithms[M].Berlin,Germany:Springer,2011:123-136.
[17] WELZL E.Smallest enclosing disks(balls and ellipsoids)[M]//MAURER H.New Results and New Trends in Computer Science.Berlin,Germany:Springer,1991:359-370.

