基于AOWEA算子的滑坡治理方案優選

李尋昌，葉君文，李 葛,2，閆成龍，趙海南

(1.長安大學地質工程與測繪學院，陜西 西安710054;2.陜西核工業工程勘察院有限公司,陜西 西安 710054)

近年來，隨著全球氣候的異常和人類工程活動的加劇，滑坡災害頻發，給人類的正常生活和生產帶來了巨大的影響和威脅，因而滑坡防治成為防災減災的熱點問題之一。在滑坡防治中，不同的治理思路和方案對治理效果、工程投資和環境影響等不盡相同，但好的治理方案不但可以穩定滑坡、降低投資、減少對環境的破壞，有時還可以起到方便施工的作用，所以在滑坡治理可研階段或初步設計階段采用合適的方法，優選出合理的治理方案供施工設計階段采用就顯得十分重要。

滑坡治理方案優選的方法歸納起來主要包括定性、半定性半定量和定量計算3種方法。如王恭先[1]提出應從滑坡性質、規模和狀態，防治目的和原則，防治措施適用條件及其適用性，經濟可行性、社會環境效益及施工技術的難易程度4個方面對滑坡治理方案進行定性選擇，但該方法要求設計人員須具有相當豐富的工程經驗；穆啟超等[2]基于定性分析的半定量優選方法，從投入資金、技術操作可行性、安全性、環境破壞和工期5個方面對某滑坡治理方案進行了優選;楊穎蓉等[3]利用最優傳遞矩陣的改進層次分析法對某邊坡治理方案進行了優化決策，但僅對不同治理方法在危巖體治理中的優劣進行了定量比選;王含秦等[4]基于安全、經濟、技術等因素建立了滑坡綜合治理方案比選體系，并采用熵權決策法對滑坡治理方案進行了定量比選，但在決策過程中未考慮優選指標之間的關系和決策者對決策的影響。

滑坡治理方案優選是決策者利用分析決策屬性信息，通過某種方法對有限個已知方案進行綜合評價，進而根據評價結果對已知方案進行排序，其優選過程是一個多目標屬性決策問題。目前多目標屬性決策在經濟[5]、軍事[6]、管理[7]、環境[8]及工程系統[9-10]等方面應用廣泛，但在滑坡治理方案優選方面應用較少。多目標屬性決策能根據決策指標體系，充分考慮決策屬性之間的權重關系，研究決策者在決策過程中的作用，系統地對決策問題進行求解，得出決策方案綜合屬性效用值，進而選擇最優決策方案。因此，本文利用多屬性決策中的上升有序加權歐氏平均(Ascending Order Weighted Enclidean Average,AOWEA)算子，對某滑坡的治理方案進行了優選，以為滑坡治理方案的優選提供思路和決策依據。

1 AOWEA算子優選的基本思路

有序加權平均(OWA)算子[11]是一種介于最大算子與最小算子之間的數據信息集成方式，它可以對所給數據按從大到小的順序重新進行排序和加權集結。近年來，該算子的研究和推廣十分廣泛，如組合加權平均(CWAA)算子[12]、模糊有序加權平均(WOWA)算子[13]、廣義有序加權平均(GOWA)算子[14]等。本文在OWA算子的基礎上，采用上升有序加權歐氏平均(AOWEA)算子[15]，對所給出的滑坡各治理方案數據按從小到大的順序重新進行排序并通過加權集結，定量計算出各治理方案的分值大小，確定出相對較優方案，以供決策者參考。

1.1 OWA算子[16-18]

設f:Rn→R+,若

(1)

1.2 AOWEA算子[19-20]

(2)

1. 3 決策矩陣

由于滑坡治理方案的選擇具有客觀復雜性，因此本文采用區間數來表示多屬性決策中的決策屬性值。

1. 4 指標屬性的規范化處理

指標屬性規范化可以消除不同量綱對決策結果的影響，根據區間數的運算法則，本文采用下面公式對區間數指標屬性進行規范化處理。

對于效益型指標：

(3)

對于成本型指標：

(4)

式中：J1、J2分別為效益型指標和成本型指標;n為評價指標的個數。

1. 5 離差最大化指標權重的確定

為了排除決策者主觀偏好對指標權重的影響，本文應用離差最大化原理求解方案優選指標的權重[21]。方案優選指標值偏差的大小表征指標權重的大小，離差最大化指標uj權重的最優解為

(5)

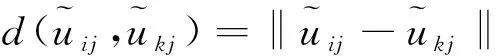
1. 6 基于AOWEA算子的方案優選

基于AOWEA算子的方案優選的具體步驟如下：

(1) 對于所優選問題，設S={S1,S2,…,Sm}為備選方案集，U={u1,u2,…,un}為指標屬性集，指標屬性權重利用離差最大化方法求解得出。對于方案Si∈S，Si關于指標uj的屬性值為aij，進而構成決策矩陣A=(aij)m×n(aij>0)。

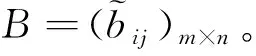
(6)

(3) 按Zi(i∈N)的大小對所有方案進行排序并優選。

2 某滑坡治理方案優選的實例分析

2. 1 某滑坡治理方案

某滑坡位于陜北黃土梁峁的斜坡地帶，東北緊靠蟠龍河，南側為延河，西鄰黃土梁峁地帶。

該滑坡體主軸方向為西南—東北方向，南北長約1 000 m，東西寬約600 m，滑坡體高差約80 m，坡角約15°。其中,Ⅰ級滑坡平均厚度為27.9 m，北側Ⅱ級滑坡平均厚度為21.49 m，南側Ⅱ級滑坡平均厚度為17.86 m，總體積為611.6×104m3，屬大型土質堆積層滑坡。該滑坡區域地形平面圖見圖1。

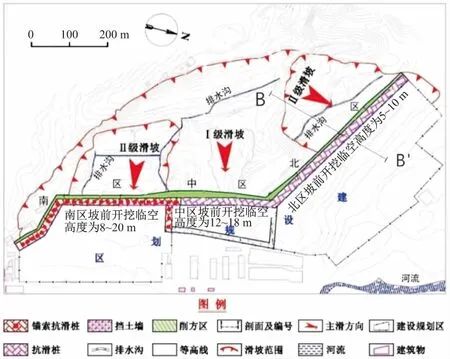
圖1 某滑坡區域地形平面圖Fig.1 Regional terrain plan of a landslide

由于工程建設，對滑坡前緣需要進行一定程度的開挖，開挖臨空面高度約5～20 m不等，該滑坡北區治理工程B-B′剖面圖見圖2。該工程建設過程中滑坡的北、中、南區的開挖基準面高程分別為928 m、932 m、921 m，這也將直接影響到原有滑坡的穩定性。為了保證工程建設的順利進行，在滑坡治理工程初步設計階段共提出4種治理方案，具體如下：

圖2 某滑坡北區治理工程B-B′剖面圖Fig.2 B-B′ Profile of treatment project in the north district of the landslide

(1) 方案一：在滑坡治理工程中區和北區開挖坡腳各設置一道截面尺寸為1.5 m×2.0 m的抗滑樁，間距為6.0 m，懸臂為5.0 m；在滑坡治理工程南區設置一道截面尺寸為3.0 m×4.0 m的錨索抗滑樁，間距為5.0～6.0 m，懸臂約為10.0 m，兩道抗滑樁深入基巖面以下約10 m,為控制樁體變形和位移，懸臂部分設置2～3道錨索；對開挖面以上坡體按懸臂部分同時輔之以坡面和坡體排水工程。

(2) 方案二:由于考慮到滑坡治理工程北區和中區開挖后穩定性較高，將抗滑樁方案調整為坡腳擋墻支擋；在滑坡治理工程南區和輔助工程與方案一一致。

(3) 方案三:在滑坡治理工程北區和中區與方案二一致；在滑坡治理工程南區將大樁方案調整為雙排樁方案，單樁截面尺寸為2.0 m×3.0 m，樁距和排距均為6.0 m，排與排之間通過2.0 m×2.0 m的連梁連接。

(4) 方案四:在滑坡治理工程北區和中區與方案二一致;在滑坡治理工程南區開挖坡腳改為單排截面尺寸2.0 m×3.0 m的錨索抗滑樁方案，但對其上坡體進行了大面積的削方卸載。

2. 2 指標體系和決策矩陣的建立

指標體系的建立是滑坡治理方案優選的重要前提，可根據滑坡特征、危害對象及防治措施等特點，選取合理、可行、有效的滑坡治理方案優選指標。

本文建立的滑坡治理方案優選指標體系為三層遞階結構(見圖3)：滑坡治理方案優選(第一層為目標層)；經濟性指標、技術性指標、環境影響指標(第二層為準則層)；屬性指標(第三層為指標層或因素層)。

基于滑坡治理方案優選指標體系，可將其分為效益型指標和成本型指標兩種，其中U11、U12、U21、U22、U23、U31、U33為成本型指標，U24和U32為效益型指標。又由于滑坡治理方案的優選具有客觀復雜性和不確定性，所以本文采用區間數來表示多屬性決策中的決策屬性值，并以此來建立屬性決策矩陣。規定：除了總投資U11、監測費U12、工程建設期U22這三個指標按照設計方案給出外，其他指標的取值范圍在[0,1]之間。專家在對滑坡各種治理方案的設計、工程預算、施工周期等因素全面認識后進行決策評價(采用問卷調查方法，邀請5位滑坡治理方面的專家，其中一位是項目評審時的評委專家，針對給出的滑坡4種治理方案，分別按照9種指標屬性決策給出相應的分值，然后取其平均值[22])，并給出各指標屬性決策矩陣，見表1。

圖3 滑坡治理方案優選指標體系Fig.3 Optimal index system of landslide treatment scheme

表1 各指標屬性決策矩陣Table 1 Decision matrix of the index attributes

本文利用公式(3)和(4)對表1的指標屬性決策矩陣進行規范化處理，得到各指標屬性的規范化決策矩陣，見表2。

表2 各指標屬性的規范化決策矩陣Table 2 Normalized decision matrix of the index attributes

根據各指標屬性的規范化決策矩陣值，利用公式(5)求得各指標的權重為

W=[wU11，wU12，wU21，wU22，wU23，wU24，wU31，wU32，wU33]

=[0.067 9,0.040 4,0.139 4,0.170 9,0.117 1,0.029 0,0.187 8,0.055 3,0.192 3]

2.3 基于AOWEA算子的滑坡治理方案優選模型與應用

2.3.1 屬性信息排序

在利用AOWEA算子進行指標屬性信息集結前，需對指標屬性信息進行排序，由于該滑坡治理方案的屬性值為區間數，兩兩之間一般無法直接進行大小比較，因此需要利用一種區間數排序方法——區間數可能度進行排序。

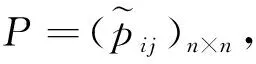
(i,j=1,2,…,n)

(7)

(i,j=1,2,…,n;k=1,2,3,4)

(8)

采用公式(7)對方案xk(k=1,2,3,4)的各個屬性指標ukj(j=1,2,…,9)進行兩兩比較，其中xk為滑坡治理的第k種方案，μkj為第k種治理方案的第j種屬性指標，并建立各個屬性指標之間的可能度矩陣Pk(k=1,2,3,4)，然后利用公式(8)計算方案的可能度矩陣排序向量Vk(k=1,2,3,4)，則可求得方案一的可能度矩陣P1為

進而得出方案一的可能度矩陣的排序向量V1為

（2）儲層發育微孔隙和微裂縫，屬于孔隙—裂縫型儲層，以孔隙為主，但微裂縫對儲集物性的影響顯著。儲集物性決定儲層的含油性，沉積規模大、厚度大的砂礫巖體物性好，含油性也好。II砂層組、III砂層組沉積厚度大，規模大，是主要含油層系。車66、車660井區位于洼陷中部東西厚砂礫巖體交匯部位，成為主要油氣聚集區。根據II、III砂層組展布特征，結合目前鉆探情況推斷，車66—車664井一帶、車66—車660井一帶，車73井向南一帶應有較好的勘探前景。

V1=[0.081 2,0.098 0,0.118 2,0.093 7,0.094 3,0.120 8,0.132 8,0.126 2,0.134 7]

同理，可得出其他方案可能度矩陣的排序向量如下：

V2=[0.111 3,0.105 7,0.095 0,0.115 5,0.126 6,0.099 8,0.121 9,0.105 8,0.118 5]

V3=[0.114 7,0.108 3,0.089 7,0.116 7,0.121 4,0.102 2,0.122 7,0.104 9,0.119 4]

V4=[0.123 5,0.118 6,0.131 4,0.131 6,0.092 7,0.100 7,0.105 8,0.087 6,0.108 1]

各種方案可能度矩陣的排序向量Vk(k=1,2,3,4)為

Vk=[V1,V2,V3,V4]T

根據各種方案可能度矩陣的排序向量，將表2中各指標屬性規范化決策矩陣的指標屬性值重新排序后，得到重新排序后的各指標屬性的規范化決策矩陣，見表3。

表3 重新排序后的各指標屬性的規范化決策矩陣Table 3 Sorted normalized decision matrix of the index attributes

2.3.2 AOWEA算子的信息集結

2.3.3 綜合屬性效用值的可能度排序

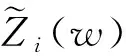
V=[0.262 7,0.243 3,0.250 2,0.243 8]

根據vi對區間數Zi(w)進行排序，即可確定該滑坡的最優治理方案。

由可能度矩陣P中的可能度及排序向量V，得到評估結果Zi(w)的排序為

實際上，該滑坡治理工程中區和北區在治理過程中沒有采取本文推薦的方案一(S1)，且存在對坡腳不合理開挖取土現象，最終導致滑坡治理工程中區和北區連接地段變形較大。另外，滑坡治理工程北區的坡腳施工工序不當，加之滑坡前緣場地建設將老滑坡原有地下水路阻擋，導致滑坡體富水較多，滑坡的穩定性較差。相比，滑坡治理工程中區和南區過渡段設有抗滑樁，從全站儀測量的監測數據可知該滑坡地表變形小，坡體上的格構也未有破壞跡象，說明抗滑樁起到了良好的阻滑效果，進而反證了本文推薦的滑坡治理方案一的合理性和有效性。

3 結 論

滑坡治理是災害治理工程中的熱點，選擇經濟、合理、有效的滑坡治理方案是開展滑坡治理工程的重要基礎。本文基于多屬性決策基本理論，提出了滑坡治理方案優選決策的新方法，并通過工程實例的具體應用，得出如下結論：

(1) 在基于上升有序加權歐氏平均算子(AOWEA)理論的基礎上，結合工程實例建立了滑坡治理方案優選模型。

(2) 以某滑坡治理工程在初步設計階段提出的4種治理方案為基礎，利用滑坡治理方案優選模型，得出該滑坡4種治理方案的優選排序結果為：S1>S3>S4>S2。在對優選排序結果簡要分析后，本文推薦方案一(S1)作為該滑坡治理的首選方案。

(3) 通過對實際治理后的滑坡進行變形監測分析和變形預測，驗證了基于AOWEA算子的滑坡治理方案優選模型的可行性、合理性和有效性，因此可將該多屬性決策方法應用到實際滑坡治理方案的優選中。

參考文獻：

[1] 王恭先.滑坡防治方案的選擇與優化[J].巖石力學與工程學報,2006,25(S2):3867-3873.

[2] 穆啟超,王萬遷,蔡鐵剛.四川地震災區某滑坡穩定性分析及治理工程方案比選[J].安全與環境工程,2011,18(4):11-16.

[3] 楊穎蓉,侯學良.淺談多目標優化決策方法[J].現代經濟信息,2013(15):80.

[4] 王念秦,姚勇,羅東海.滑坡綜合治理方案比選評價模型[J].水土保持通報,2009,29(1):111-114.

[5] 汪賽,李新春,彭紅軍.基于安全效益分析的煤炭企業安全投入決策模型[J].統計與決策,2009(5)：52-54.

[6] 姜寧.電子對抗仿真系統中的多屬性決策理論模型與方法研究[D].大連:大連理工大學,2000.

[7] 王志良.水資源管理多屬性決策與風險分析理論方法及應用研究[D].成都:四川大學,2003.

[8] 劉明星.基于多屬性決策的海洋環境下裝備優選方法研究[D].長沙:國防科學技術大學,2009.

[9] 陳麗.水利工程規劃方案多屬性決策評價體系構建及評價方法研究[D].天津:河北工業大學,2012.

[10]何萬里.關于多屬性決策的一種新的區間數排序方法[J].價值工程,2013,32(3):303-304.

[11]Yager R R.On ordered weighted averaging aggregation operators in multicriteria decision making[J].IEEETransactionsonSystems,Man,andCybernetics,1988,18(1):183-190.

[12]徐澤水.幾類多屬性決策方法研究[D].南京：東南大學,2003.

[13]Torra V.The weighted OWA operator[J].InternationalJournalofIntelligentSystems,1997,12:153-166.

[14]Yager R R.Generalized OWA aggregation operators[J].FuzzyOptimizationDecisionMaking,2004,3(1):93-107.

[15]許葉軍,達慶利.上升有序加權歐氏平均算子及其在決策中的應用[J].南京工程學院學報(自然科學版),2004,2(3):35-39.

[16]樊治平,李洪燕,姜艷萍.基于OWA算子的群決策方法的靈敏度分析[J].東北大學學報(自然科學版),2004,25(11):1114-1117.

[17]Nadi S,Delavar M R.Multi-criteria,personalized route planning using quantifier-guided ordered weighted averaging operators[J].InternationalJournalofAppliedEarthObservationandGeoinformation,2011,13(3):322-335.

[18]Wang Z J.A note on “A group decision making model based on a generalized ordered weighted geometric average operator with interval preference matrices” [J/OL].FuzzySetsandSystems,2017(2017-05-04).https://doi.org/10.1016/j.fss.2017.04.018.

[19]Wei C.An induced OWA operator in coal mine safety evaluation[J].JournalofComputerandSystemSciences,2012,78(4):997-1005.

[20]Xu Z S,Da Q L.The ordered weighted geometric averaging operators[J].InternationalJournalofIntelligentSystems,2002,17(7):709-716.

[21]戚彥龍,王琨,朱星輝,等.基于離差最大化原理的航班延誤風險分級研究[J].武漢理工大學學報(交通科學與工程版),2014,38(1):162-166.

[22]蔣英杰,孫志強,李龍,等.基于專家判斷的行為形成因子評分方法[J].安全與環境工程,2012,19(1):77-81,86.

[23]王茶香，吳連發.基于可能度排序法的區間信息指派方法[J].數學的實踐與認識,2008,38(21):150-155.