第二十二講 混料均勻設(shè)計(jì)簡(jiǎn)介

徐靜安

在混料試驗(yàn)中，分量組分至少有3種，而每個(gè)分量組分Xi的含量百分比總和等于1，試驗(yàn)響應(yīng)值Y僅與Xi的百分比有關(guān)，各個(gè)分量是不獨(dú)立的。

過去，傳統(tǒng)的試驗(yàn)研究把單因素考察作為研究方案的主體方法，現(xiàn)在的試驗(yàn)研究方案：?jiǎn)我蛩乜疾焯剿髟囼?yàn)—多元素試驗(yàn)設(shè)計(jì)優(yōu)化試驗(yàn)—穩(wěn)定性驗(yàn)證試驗(yàn)。原因之一是單因素考察在簡(jiǎn)便，直觀的同時(shí)存在一定的局限性。單因素考察應(yīng)用時(shí)，實(shí)際上默認(rèn)研究對(duì)象的各個(gè)因子之間試驗(yàn)不相關(guān)，各個(gè)因子對(duì)Y沒有交互作用。

量大面廣的混料配方試驗(yàn)，其各個(gè)分量是相關(guān)而不獨(dú)立的，基于直角坐標(biāo)的傳統(tǒng)單因素方法，在混料配方試驗(yàn)中會(huì)造成分量間的隱性混雜。此外，傳統(tǒng)方法在尋優(yōu)效率等方面也受到極大挑戰(zhàn)。所以，逐步開發(fā)并形成回歸試驗(yàn)設(shè)計(jì)的各種方法。

一、混料回歸設(shè)計(jì)的技術(shù)進(jìn)展

對(duì)于混料配方試驗(yàn)方案，數(shù)理統(tǒng)計(jì)學(xué)家作出了很大努力。Scheffe在1958年在正單形坐標(biāo)體系基礎(chǔ)上提出了單純形格子點(diǎn)法，1963年提出了單純形質(zhì)心法。Cornell提出了軸設(shè)計(jì)法，并在1990年對(duì)經(jīng)典的混料設(shè)計(jì)作了綜合介紹。

經(jīng)典的混料設(shè)計(jì)討論了分量組分無約束、下限約束、有上下限約束的試驗(yàn)設(shè)計(jì)及增強(qiáng)方案，采用全回歸法統(tǒng)計(jì)建模。部分內(nèi)容見本刊2018年第一期刊登的第二十一講“混料配方研究中極端頂點(diǎn)設(shè)計(jì)的應(yīng)用解讀”。MINITAB軟件相應(yīng)模塊支持經(jīng)典的混料設(shè)計(jì)方案及計(jì)算。

在經(jīng)典混料回歸設(shè)計(jì)應(yīng)用過程中，又發(fā)現(xiàn)了一些問題：（1）實(shí)驗(yàn)點(diǎn)（不同的配方）局部相對(duì)密集，也就是在考察范圍內(nèi)，點(diǎn)集TP布點(diǎn)不夠均勻；（2）界面點(diǎn)過多，在無下限約束中，某些分量組分為零，缺少某組分的化學(xué)反應(yīng)，或不起化學(xué)反應(yīng)、或生成另一種產(chǎn)品。

發(fā)現(xiàn)問題和解決問題是創(chuàng)新的導(dǎo)向。

王元、方開泰于20世紀(jì)80年代初應(yīng)用數(shù)論方法提出均勻設(shè)計(jì)。為了克服經(jīng)典混料設(shè)計(jì)存在的問題，于1990年提出混料均勻設(shè)計(jì)。其中，有上、下限約束的混料均勻設(shè)計(jì)問題較為復(fù)雜。王元、方開泰先是按隨機(jī)過程在蒙脫卡洛逆變換基礎(chǔ)上進(jìn)行布點(diǎn)，2000年改用條件分布方法。中國均勻設(shè)計(jì)學(xué)會(huì)有相應(yīng)軟件支持。

唐啟義開發(fā)的數(shù)據(jù)處理系統(tǒng)（DPS）軟件相應(yīng)模塊平衡了混料設(shè)計(jì)經(jīng)典方法的統(tǒng)計(jì)優(yōu)良性和試驗(yàn)點(diǎn)分布均勻性，用均方誤差準(zhǔn)則（MSE）開發(fā)了定向優(yōu)化算法。上海化工研究院技術(shù)開發(fā)中心已購置正版DPS數(shù)據(jù)處理系統(tǒng)軟件給以支持。

二、混料均勻設(shè)計(jì)

基本思想是將n個(gè)試驗(yàn)點(diǎn)（n種不同的配方）均勻地分布在TP上。對(duì)于混料中分量P個(gè)組分無約束的混料均勻設(shè)計(jì)相對(duì)簡(jiǎn)單，DPS等軟件均采用方開泰等提出的逆變換方法構(gòu)筑設(shè)計(jì)方案。具體步驟如下所示：

（1）根據(jù)考察的分量個(gè)數(shù)P，選定的實(shí)驗(yàn)方案實(shí)驗(yàn)次數(shù)n，選擇等水平均勻設(shè)計(jì)表Un*（nl）或Un（nl）。均勻設(shè)計(jì)表所能安排的因素個(gè)數(shù)l一般要大于考察的分量個(gè)數(shù)P，根據(jù)使用表選擇P-1列進(jìn)行變換。

（2）用 {qji}表示所選均勻表第j列中的第i（i=1，2，…，n）個(gè)元素（水平數(shù)而不是具體的水平值）進(jìn)行轉(zhuǎn)換。

（3）將｛Cji｝轉(zhuǎn)換成｛Xji｝

于是 {Xji}就給出了對(duì)應(yīng)TP的配方均勻設(shè)計(jì)方案，并用代號(hào)UMn（np）或UMn*（np）表示，對(duì)于分量無約束的混料均勻設(shè)計(jì)，有關(guān)專著、軟件均采用此變換。《試驗(yàn)設(shè)計(jì)與數(shù)據(jù)處理》（李云雁、胡傳榮編著）附錄給出了系列UMn（np）、UMn*（np）配方均勻設(shè)計(jì)表供選擇。DPS軟件在“試驗(yàn)設(shè)計(jì)”——均勻設(shè)計(jì)“——混料均勻設(shè)計(jì)”功能模塊中均能獲得相應(yīng)的混料均勻設(shè)計(jì)方案。

為何要對(duì)常用的均勻設(shè)計(jì)表進(jìn)行這樣的變換？

Un（nl）或Un*（nl）均勻設(shè)計(jì)表適用于多維空間的直角坐標(biāo)系均勻布點(diǎn)。而混料試驗(yàn)∑Xi=1，其分量是不獨(dú)立的，適用于多維空間的單形坐標(biāo)系，經(jīng)過上述變換，UMn（np）、UMn*（np）混料均勻設(shè)計(jì)表才能體現(xiàn)在單形坐標(biāo)系中的均勻布點(diǎn)。

為了直觀了解變換過程及變換效果，對(duì)其進(jìn)行進(jìn)一步解讀；

對(duì)于P=3，n=7的案例，可選方案U7*（74），根據(jù)U7*（74）使用表，（P-1）=2，選1，3兩列，即對(duì)U7*（72）兩列進(jìn)行變換（見表1、表2）。

表1U7*（74）

表2U7*（74）的使用

對(duì)于P=3，上述變換計(jì)算可簡(jiǎn)化成如下形式：

當(dāng)i=1時(shí)，表中第1列第1個(gè)元素q11=1，而選中的第2個(gè)分量列的第1個(gè)元素q21=5，可得：

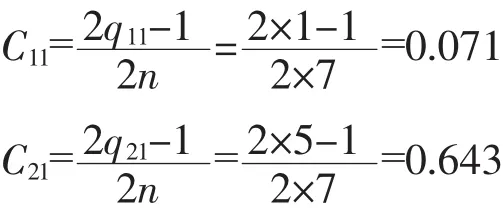
進(jìn)一步計(jì)算：

同理，可通過計(jì)算得到{Xji}，形成表3。

表3UM7*（73）及其形成過程

經(jīng)變換計(jì)算，X1+X2+X3≈1，對(duì)試驗(yàn)結(jié)果影響不大。具體計(jì)算已由專用軟件完成，對(duì)我們應(yīng)用者而言，知其然，也知其一點(diǎn)所以然。需要強(qiáng)調(diào)的是，對(duì)分量無約束的混料回歸設(shè)計(jì)，在變換成混料均勻設(shè)計(jì)時(shí)，對(duì)∑Xi=1中各分量是一視同仁的。但在統(tǒng)計(jì)建模時(shí)，（P-1）變換時(shí)選中的分量進(jìn)入模型。

進(jìn)一步分析變換方案效果：對(duì)于｛p，d｝=｛3，2｝的經(jīng)典混料回歸設(shè)計(jì)，單純形質(zhì)心法試驗(yàn)設(shè)計(jì)方案見表4。

表4 單純形質(zhì)心法試驗(yàn)設(shè)計(jì)

上述方案中，7組試驗(yàn)中有6組試驗(yàn)出現(xiàn)分量為“0”，除了7號(hào)試驗(yàn)，6組試驗(yàn)的布點(diǎn)均為界面點(diǎn)，對(duì)涉及化學(xué)反應(yīng)的混料試驗(yàn)，從專業(yè)知識(shí)上也難以接受。此外，7次試驗(yàn)僅對(duì)Xi分量考察了4個(gè)水平，效率也不是很高。

曾經(jīng)設(shè)想把X3作為“陪襯”，直接將X1，X2按獨(dú)立變量進(jìn)行均勻設(shè)計(jì)選表而不進(jìn)行變換，具體試驗(yàn)方案中按X3=1-X1-X2求取。選U7*（74）表中1，3列，結(jié)果見表5。

表5 U7*（74）的應(yīng)用及結(jié)果

上述方案中，7組試驗(yàn)有2組分量為“0”（X1，X2），如果總體分析，計(jì)及 X3，仍有 6 組分量為“0”。此外，3、6、7號(hào)試驗(yàn)歸一化處理后，也較大地影響了U7*（74）表的均勻性，且X3亦僅考察了3個(gè)水平，此方案也不理想。為此，開發(fā)了UMn（nP）混料均勻設(shè)計(jì)表，見圖 1～3。

圖1 經(jīng)典混料回歸設(shè)計(jì)的單純形質(zhì)心法布點(diǎn)

圖2U7*（74）均勻設(shè)計(jì)布點(diǎn)圖

圖3混料均勻設(shè)計(jì)UM7*（73）布點(diǎn)圖

三、有約束的混料均勻設(shè)計(jì)

在實(shí)際混料試驗(yàn)中，除了∑Xi=1的約束條件，各分量還受上下限約束，如 0≤ai≤xi≤bi≤1，i=1，2，…，p。

本文先行討論有下界約束的試驗(yàn)設(shè)計(jì)。

有下界約束的單純形設(shè)計(jì)在單形坐標(biāo)系中能準(zhǔn)確描述混料組分間的關(guān)系，一般用正單形，如正三角形、正四面體、……，P維單形即（P-1）的單純形。為便于討論，以P=3，P-1=2維的平面單純形為例，給以各分量下界約束ai，如圖4所示。

圖4 有下界約束的單純形配方設(shè)計(jì)

由圖4可見，有下界約束的單純形試驗(yàn)范圍形成了一個(gè)小的單純形，也就是在對(duì)各分量給以下界約束的同時(shí)，也轉(zhuǎn)化為對(duì)相應(yīng)分量的上界約束。

此時(shí)自然變量Xi轉(zhuǎn)換成規(guī)范變量（編碼值）或稱為“擬分量”Zi。轉(zhuǎn)換公式為：

其中 ，Xi≥ai，∑ai＜1。

可以認(rèn)為上述轉(zhuǎn)換對(duì)多分量正單形都是適用的，相關(guān)專著討論至此，仍轉(zhuǎn)入經(jīng)典的混料格子點(diǎn)設(shè)計(jì)。筆者認(rèn)為，按照類比思維僅有下界約束的正單形試驗(yàn)范圍轉(zhuǎn)化為一個(gè)小的正單形，可通過擬分量Zi轉(zhuǎn)化為無約束的正單形混料均勻設(shè)計(jì)，即可選用UMn*（np）或UMn（np）混料均勻表。

相關(guān)專著及軟件對(duì)此轉(zhuǎn)換功能尚未充分挖掘，值得探索應(yīng)用。這樣構(gòu)筑的混料均勻設(shè)計(jì)有良好的試驗(yàn)設(shè)計(jì)性質(zhì)。從應(yīng)用角度來看，這是本講座開發(fā)的新的知識(shí)點(diǎn)。

按照發(fā)散思維，進(jìn)一步引伸在混料試驗(yàn)中，分量受上下限約束是通常遇到的工程問題。在正單形坐標(biāo)系中，圖5所示對(duì)各分量給以ai下限約束，以P-1=3-1=2的正單純形為例，轉(zhuǎn)化為對(duì)各分量的上限約束，則：

中學(xué)的平面幾何即可證明：

所以實(shí)際混料試驗(yàn)的上下限約束，如果能調(diào)整到符合上述約束條件，仍能形成擬分量Zi無約束的正單形，方便地使用混料均勻設(shè)計(jì)表。

四、案例

試制某種火箭推進(jìn)劑，三種混料成分受下限約束。

黏結(jié)劑 X1≥0.2；氧化劑 X2≥0.4；燃料 X3≥0.2。

試驗(yàn)?zāi)康臑椋夯炝吓浞綇椥阅?shù)大于3000，并且黏結(jié)劑用量盡可能少。

彈性模數(shù)亦稱“彈性模量”或“彈性系數(shù)”，是材料在彈性極限內(nèi)應(yīng)力同應(yīng)變的比值，反映材料抵抗應(yīng)變的能力。材料的彈性極限隨溫度的升高而減小。顯然，本案例是在固定過程參數(shù)溫度的條件下進(jìn)行配方混料設(shè)計(jì)。這是一個(gè)典型的有下界約束的混料試驗(yàn)問題。其實(shí)驗(yàn)考察范圍是在P-1=3-1=2的單純形中形成的小正三角形，由于a1=0.2，a2=0.4，a3=0.2，1-∑ai=1-（0.2+0.4+0.2）=0.2＜1，所以考察范圍內(nèi)小正三角形內(nèi)任意一點(diǎn)的坐標(biāo)關(guān)于自然空間與編碼空間之間的轉(zhuǎn)換關(guān)系為：

在實(shí)際試驗(yàn)時(shí)，假定采用不同的方案。

（1）單配方考察試驗(yàn)，即傳統(tǒng)的混料試驗(yàn)方案

表6 單配方考察試驗(yàn)結(jié)果

通過7次單配方的考察，7號(hào)試驗(yàn)的彈性模數(shù)為3 000，考慮到誤差，要求Y＞3 000，尚應(yīng)在7號(hào)試驗(yàn)Xi附近追加試驗(yàn)。由于混料試驗(yàn)分量不獨(dú)立，難以單獨(dú)判斷分量的“好點(diǎn)”方向。所以需在此基礎(chǔ)上追加2×P組單配方考察試驗(yàn)，工作量相對(duì)較大。而在相同試驗(yàn)次數(shù)下，可提取的信息量有限，試驗(yàn)效率不高，特別是對(duì)專業(yè)知識(shí)經(jīng)驗(yàn)的依賴性更強(qiáng)。

（2）單純形質(zhì)心設(shè)計(jì)，即經(jīng)典的混料設(shè)計(jì)方案

表7 單純形質(zhì)心設(shè)計(jì)結(jié)果

上述構(gòu)成經(jīng)典的{p，d}={3，2}三分量二階單純形質(zhì)心設(shè)計(jì)，可用Scheffe不完全三次多項(xiàng)式擬合，求得Y對(duì)編碼“擬分量”的全回歸方程。因本文重點(diǎn)并非討論經(jīng)典三分量二階單純形質(zhì)心設(shè)計(jì)，限于篇幅計(jì)算過程略，有興趣的讀者可查閱相關(guān)資料。讀者應(yīng)用時(shí)，MINITAB，DPS有相應(yīng)模塊計(jì)算支持。

可得：Y=2 350Z1+2 450Z2+2 650Z3+1 000Z1Z3+1 600Z2Z3+6 150Z1Z2Z3

此編碼三分量混料體系的約束條件：

對(duì)上述Scheffe多項(xiàng)式全回歸方程作個(gè)說明，方程中缺 Z1Z2項(xiàng)，經(jīng)過筆者計(jì)算驗(yàn)證：b12=4Y12-2（Y1+Y2）=4×2 400-2×（2 350+2 450）=0，所以該項(xiàng)可略。對(duì)混料設(shè)計(jì)的結(jié)果進(jìn)行分析，由于分量不獨(dú)立，應(yīng)在單形坐標(biāo)系中的Y等值線圖上進(jìn)行。按滿足Z1≥Z1min 選擇混料優(yōu)化點(diǎn)配方：Z1=0.05，Z2=0.41，Z3=0.54，預(yù)報(bào)Y=3 002.24，相對(duì)應(yīng)的自然分量X1=21%、X2=48.2%、X3=30.8%，驗(yàn)證值為Y=3 010。

經(jīng)典的單純形質(zhì)心設(shè)計(jì)比傳統(tǒng)的單配方試驗(yàn)效率大為提高，數(shù)據(jù)處理更加規(guī)范、可行。

（3）混料均勻設(shè)計(jì)，即現(xiàn)代混料設(shè)計(jì)方案

UM7*（73）及其生成過程如表8所示。

表8UM7*（73）及其生成過程

從U7*（72）均勻表逆變換成混料均勻設(shè)計(jì)表UM7*（73），本文已前述，可直接查表及在DPS軟件模塊中生成。需要說明的是，UMn*（nl）適用于混料無約束及約束可形成正單形的場(chǎng)合。當(dāng)約束形成正單形時(shí)，表中Xi應(yīng)由“擬分量”Zi替代。結(jié)合本案例，選用UM7*（73）表后，具體的試驗(yàn)方案（見表9），需從編碼空間Zi轉(zhuǎn)換成自然空間的Xi。

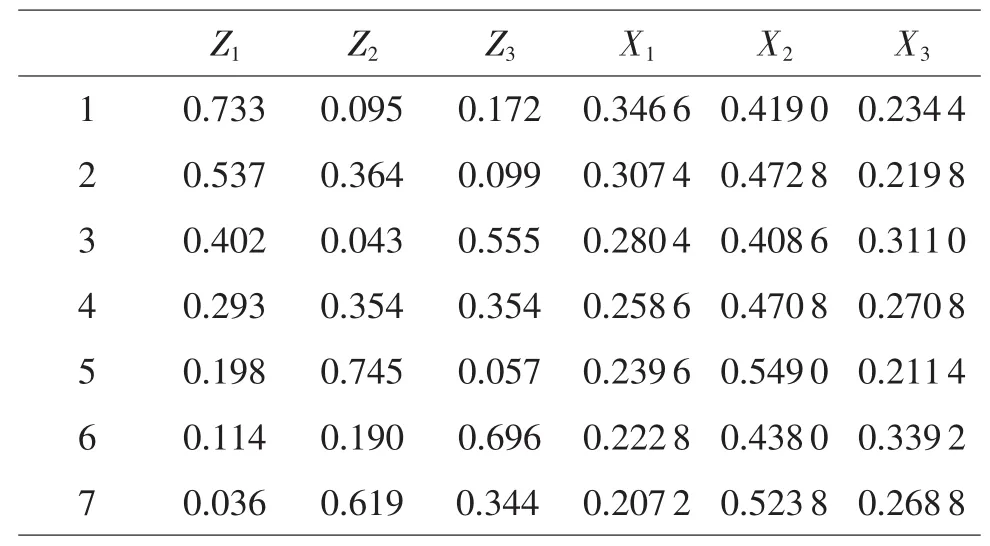
表9 UM7*（73）具體的試驗(yàn)方案

在相同的實(shí)驗(yàn)樣本量n=7次條件下：傳統(tǒng)單配方考察，考察分量4個(gè)水平，難以建模，尚需追加實(shí)驗(yàn)；經(jīng)典單純形質(zhì)心設(shè)計(jì)，考察分量4個(gè)水平，可以建模，但邊界點(diǎn)過多；現(xiàn)代混料均勻設(shè)計(jì)考察分量7個(gè)水平，均勻性更好，可以建模。本講座第一講“統(tǒng)計(jì)模型的假定和變量水平的設(shè)定”，已證明在相同的條件下，多水平設(shè)計(jì)比重復(fù)水平設(shè)計(jì)效率更高，模型穩(wěn)定性更好。對(duì)本文討論的內(nèi)容作一簡(jiǎn)單歸納，混料均勻設(shè)計(jì)方案構(gòu)筑，建模及變換的邏輯框圖見圖6。

圖6 混料均勻設(shè)計(jì)方案構(gòu)筑、建模及變換的邏輯框圖

借用中央人才工作協(xié)調(diào)小組指導(dǎo)的《中國人才》2014年10月刊（總第463期）中“退讓的智慧”一文中的一段話，與君共勉。寒山曾問拾得：“世間謗我、欺我、辱我、笑我、賤我、惡我、騙我，如何處治乎”？拾得說：“只是忍他、讓他、由他、避他、耐他、敬他、不要理他，再待幾年且看他。”靜心做好該做、想做的事。在創(chuàng)新開發(fā)中，學(xué)習(xí)應(yīng)用新技術(shù)不可避免地會(huì)有坎坷、挫折甚至失敗，會(huì)因被誤解、低估而感到孤獨(dú)。青年同仁們，當(dāng)前的科研環(huán)境已經(jīng)有了很大變化，但仍需忍耐、堅(jiān)持，不斷學(xué)習(xí)應(yīng)用新技術(shù)、新方法。

“混料配方研究中極端項(xiàng)點(diǎn)設(shè)計(jì)的應(yīng)用解讀”介紹的是經(jīng)典方法，本文介紹的是能形成正單形的現(xiàn)代混料均勻設(shè)計(jì)。對(duì)于上、下限約束不能形成正單形的混料均勻設(shè)計(jì)，將在后續(xù)討論，讓我們同行。