由部分特征值和順序主子陣構(gòu)造廣義Jacobi矩陣的逆特征值問題*

潘云蘭, 秦 立

(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華 321004)

0 引 言

本文討論的廣義Jacobi矩陣Gp,q是指具有如下形狀的矩陣:

(1)

式(1)中:γi=βi(i=p,p+1,…,q-1);αp,αp+1,…,αq,βp,βp+1,…,βq-1都為復(fù)數(shù).簡記Gk=G1,k.

1979年,Hochstadt[1]提出了著名的重構(gòu)Jacobi矩陣的逆特征值問題(問題DD).

文獻(xiàn)[2]證明了問題DD等價于如圖1的質(zhì)量-彈簧系統(tǒng)的逆振動問題.

圖1 質(zhì)量-彈簧系統(tǒng)逆振動問題示意圖

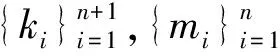
由于在質(zhì)量-彈簧系統(tǒng)實驗中很難得到所有的特征值,所以問題DD′常常被修正為如下的問題MD′:

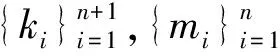
文獻(xiàn)[2-4]對問題MD′的研究進(jìn)一步歸結(jié)為如下的問題:

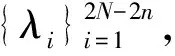
文獻(xiàn)[1,5-10]都深入地研究了問題DD.文獻(xiàn)[1]證明了“若問題DD的解存在,則必唯一”；文獻(xiàn)[5]給出了問題DD有解的充分必要條件；文獻(xiàn)[6]改進(jìn)并完善了Dai的理論,提出了問題DD有解的另一個充分必要條件,并且提供了一個求解問題DD的算法；文獻(xiàn)[6-10]分別提出了不同的數(shù)值算法去求解問題DD.而問題MD是問題DD的推廣.盡管問題DD已經(jīng)得到了深入的研究,但所采用的算法并不能夠直接應(yīng)用于問題MD,主要原因是問題MD中特征值只是部分給定的.

本文受問題MD的啟發(fā),討論問題GMD.

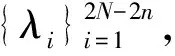
接下來首先給出問題GMD有解的充分必要條件;然后給出數(shù)值算法;最后用數(shù)值例子檢驗算法的有效性.

本文記Ik為k階單位矩陣,ei為單位矩陣的第i列,其大小根據(jù)實際情況而定,xT為x的轉(zhuǎn)置,det(X)為矩陣X的行列式,Gk為GN的k階順序主子陣,Gl,k為GN刪除前面的l-1行,l-1列,以及后面的N-k行,N-k列后所剩下的k-l+1階主子陣.令

φk(λ)=det(λIk-Gk),φl,k(λ)=det(λIk-l+1-Gl,k).

1 主要結(jié)果

下面將給出問題GMD有解的充分必要條件.先將GN作如下分塊處理:

(2)

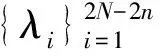
(3)

當(dāng)Gn給定時,φn(λ),φn-1(λ)給定,所以φN(λ)將由βn,φn+1,N(λ)和φn+2,N(λ)決定.

(4)

下面將證明,求βn及φn+1,N(λ)和φn+2,N(λ)的系數(shù)可轉(zhuǎn)化為求下列線性方程組的解:

V0x=-y.

(5)

式(5)中:

(6)

(7)

先給出復(fù)數(shù)域上的根分離定理.對一個復(fù)數(shù)γ,其實部和虛部分別記為γR和γI.

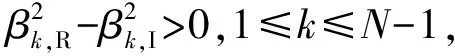
1)若Gk-1和Gk+1,N的特征值實部兩兩不同,則

λ1,R<ξ1,R<λ2,R<ξ2,R<…<ξp,R<λp+1,R<ξp+1,R<…<λN-1,R<ξN-1,R<λN,R.

(8)

2)若Gk-1和Gk+1,N的特征值中有相同的實部,不妨設(shè)ξp,R=ξp+1,R,則除了用ξp,R=λp+1,R=ξp+1,R替換ξp,R<λp+1,R<ξp+1,R外,式(8)仍成立,且有ξp,I<λp+1,I<ξp+1,I.

證明 記置換矩陣

則

(9)

式(9)中:yT=(0,0,…,0,βk-1,βk+1,0,…,0)是N-1元向量;βk-1和βk+1分別是其第k-1個和第k個分量.從而

(10)

記(x1,x2,…,xN-1)為Wk的特征向量組成的酉矩陣,則

(11)

(12)

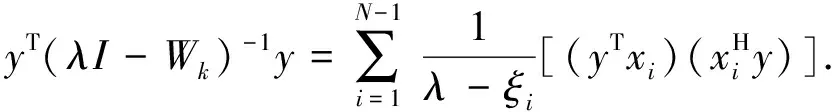
(13)

(14)

(15)

下證引理1中的結(jié)論1),此時，ξ1,R,ξ2,R,…,ξN-1,R互不相同.易知

(16)

即ξ1,ξ2,…,ξN-1不是det(λI-GN)=0的根.因此,det(λI-GN)=0等價于

(17)

而

(18)

式(18)中:Ai=λR-ξi,R;Bi=λI-ξi,I.由此可得

(19)

(20)

由以上性質(zhì)及函數(shù)的連續(xù)性,即得λ1,R<ξ1,R<λ2,R<ξ2,R<…<λN-1,R<ξN-1,R<λN,R.故結(jié)論1)成立.

下證引理1中的結(jié)論2),此時，ξ1,R,ξ2,R,…,ξN-1,R有相同值，不妨設(shè)ξp,R=ξp+1,R.下面根據(jù)虛部情況分情形1(虛部不同)和情形2(虛部相同)進(jìn)行證明.

情形1虛部不同，即ξp,I≠ξp+1,I.類似于上面關(guān)于結(jié)論1)的證明可得ξp,R=λp+1,R=ξp+1,R.由式(20)可得

所以,ξp,I<λp+1,I<ξp+1,I.

情形2虛部也相同，即ξp,I=ξp+1,I，此時,ξp=ξp+1.類似于結(jié)論1)的證明可知，ξp和ξp+1都不是det(λI-GN)=0的根.由式(15)可得

因此，ξp=λp+1=ξp+1,從而，ξp,R=λp+1,R=ξp+1,R.令

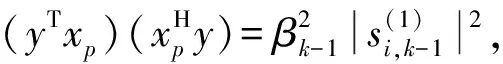
(21)

當(dāng)λ→ξp時,式(21)的第2部分是第1部分的高階無窮小量,故只需對第1部分進(jìn)行分析.

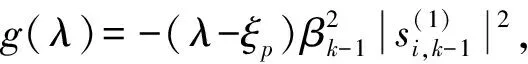
又因為ξp=ξp+1,同理可得

由以上性質(zhì)可推得ξp,I<λp+1,I<ξp+1,I,λ1,R<ξ1,R<λ2,R<ξ2,R<…<λp-1,R<ξp-1,R<λp,R<ξp,R=λp+1,R=ξp+1,R<λp+2,R<…<λN-1,R<ξN-1,R<λN,R成立.

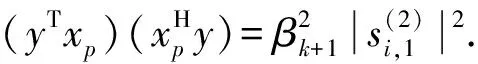
綜上所述,結(jié)論2)成立.引理1證畢.

文獻(xiàn)[11]在實數(shù)情形下給出了Gn+1,N和Gn+2,N存在的充分必要條件.結(jié)合引理1,不難得到以下引理:

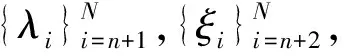
由文獻(xiàn)[12]中的引理2不難得到以下引理:

引理3若問題GMD有解,則

下面給出本文的主要結(jié)果.

定理1設(shè)x=[x1,x2,…,x2t]T是式(5)的根,

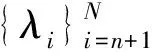
1)V0非奇異;

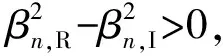
證明 先證明必要性.假設(shè)GN是問題GMD的解.由引理3可得V0非奇異,故條件1)成立.

(22)

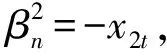
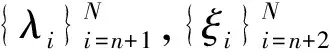
f(λ)=det(λIt-Gn+1,N),g(λ)=x2tdet(λIt-1-Gn+2,N).

(23)

將式(23)代入式(2)，再注意到條件2),即得

φN(λ)=φn(λ)f(λ)+φn-1(λ)g(λ).

因此，對1≤k≤2t,

由式(5)知

(24)

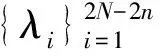
2 數(shù)值算法

總結(jié)以上討論,可得如下求解問題GMD的算法:

步驟1:求Gn,Gn-1的特征多項式φn(λ),φn-1(λ).

步驟2:由式(6)和式(7)構(gòu)造V0,y.若V0是非奇異的,則轉(zhuǎn)到步驟3;否則,無解,終止算法.

步驟3:通過式(5)求x=[x1,x2,…,x2t]T.

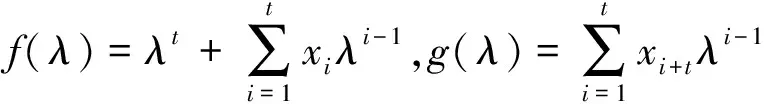
步驟6:根據(jù)引理2,得到滿足條件的Gn+1,N和Gn+2,N.

步驟7:由式(2)得到矩陣GN.

3 數(shù)值例子

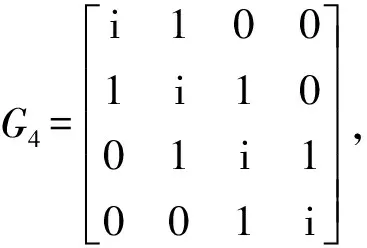
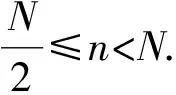
步驟1:求得G4,G3的特征多項式為

φ4(λ)=λ4-4iλ3-9λ2+10iλ+5;φ3(λ)=λ3-3iλ2-5λ+3i.

步驟2:構(gòu)造V0,y如下：

經(jīng)過檢驗,det(V0)≠0.

步驟3:根據(jù)式(5),算得x=[-2,-2i,i,-1]T.

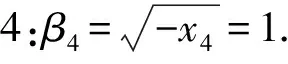
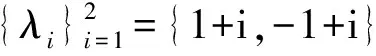
步驟6:根據(jù)引理2,可得滿足所需條件的G5,6,G6,6.

步驟7:由式(2)得到矩陣G6：

4 結(jié) 語

從以上例子可以發(fā)現(xiàn),問題GMD是問題GDD的推廣.這在很多方面都為我們進(jìn)一步研究問題DD和問題GDD拓寬了思路,奠定了更好的基礎(chǔ).引理1對非對角元元素有一定的限制,如何求解關(guān)于無限制非對角元元素的問題GMD,筆者將在今后做進(jìn)一步的研究.

參考文獻(xiàn)：

[1]Hochstadt H.On the construction of a Jacobi matrix from mixed given data[J].Linear Algebra Appl,1979,28(28):113-115.

[2]Chu M T,Golub G H.Structured inverse eigenvalue problems[J].Acta Numer,2002,11(1):1-71.

[3]Gladwell G M L.Inverse problems in vibration[M].2nd.Dordrecht：Kluwer Academic Publishers,2004.

[4]Nylen P,Uhlig F.Inverse eigenvalue problem:Existence of special spring-mass systems[J].Inverse Problems,1997,13(13):1071.

[5]周樹荃，戴華.代數(shù)特征值反問題[M].鄭州:河南科學(xué)技術(shù)出版社,1991.

[6]Xu Shufang.On the Jacobi matrix inverse eigenvalue problem with mixed given data[J].SIAM J Matrix Anal Appl,1996,17(3):632-639.

[7]Boley D,Golub G H.A survey of matrix inverse eigenvalue problems[J].Inverse Problems,1987,3(4):595.

[8]Liang Haixia,Jiang Erxiong.An inverse eigenvalue problem for Jacobi matrices[J].J Comput Math,2007,25(5):620-630.

[9]Wu X.A divide and conquer algorithm on the double dimensional inverse eigenvalue problem for Jacobi matrices[J].Appl Math Comput,2012,219(8):3840-3846.

[10]Wu X,Jiang E.A new algorithm on the inverse eigenvalue problem for double dimensional Jacobi matrices[J].Linear Algebra Appl,2012,437(7):1760-1770.

[11]Hald O H.Inverse eigenvalue problems for Jacobi matrices[J].Linear Algebra Appl,1976,14(1):63-85.

[12]Wei Y.A Jacobi matrix inverse eigenvalue problem with mixed data[J].Linear Algebra Appl,2015,466(10):2774-2783.