κ?μ陰影衰落信道下非數(shù)據(jù)輔助的誤差矢量幅度性能分析

楊凡，曾孝平，毛海偉，簡(jiǎn)鑫，杜得榮，譚曉衡，高乙文

（1. 重慶大學(xué)通信工程學(xué)院，重慶 400044；2. 重慶金美通信有限責(zé)任公司，重慶 400030；3. 中國(guó)移動(dòng)通信集團(tuán)重慶有限公司，重慶 400044）

1 引言

κ?μ陰影衰落信道作為一種廣義的衰落信道，由Yacoub[1]首次提出，它具有與實(shí)際信道測(cè)試數(shù)據(jù)一致性好且能退化為多種典型衰落信道（Rice信道和Nakagami-m信道等）的特點(diǎn)[2]。κ?μ陰影衰落信道下的性能預(yù)測(cè)可為自適應(yīng)調(diào)制策略設(shè)計(jì)、傳輸容量?jī)?yōu)化等無(wú)線通信中的關(guān)鍵技術(shù)提供有效的理論參考而受到國(guó)內(nèi)外的廣泛關(guān)注。但由于在κ?μ陰影衰落信道下尚未給出理論的性能界限，無(wú)法給實(shí)際的系統(tǒng)設(shè)計(jì)提供有效的理論依據(jù)，因此，如何選擇信道評(píng)估參量并在κ?μ陰影衰落信道下進(jìn)行性能分析就成為研究的核心問(wèn)題。

信道質(zhì)量分析的關(guān)鍵在于評(píng)估信道的物理量能夠?qū)崟r(shí)準(zhǔn)確地反映信道變化。一般常采用誤比特率（BER, bit error rate）和接收符號(hào)的信噪比（SNR,signal to noise ratio）來(lái)進(jìn)行準(zhǔn)靜態(tài)信道的質(zhì)量評(píng)估[3]，而應(yīng)用在κ?μ陰影衰落信道下，BER因?yàn)樾枰鶕?jù)譯碼后的結(jié)果進(jìn)行統(tǒng)計(jì)，統(tǒng)計(jì)結(jié)果遠(yuǎn)滯后于信道變化；SNR估計(jì)常依賴于輔助數(shù)據(jù)（如前導(dǎo)符號(hào)和導(dǎo)頻符號(hào)）完成，也存在由于輔助數(shù)據(jù)間的固定時(shí)間間隔導(dǎo)致信道評(píng)估的非實(shí)時(shí)性誤差。隨著研究的深入，研究人員提出將誤差矢量幅度（EVM, error vector magnitude）作為特征參量，在時(shí)變衰落信道下評(píng)估信道質(zhì)量的變化[4～6]。將EVM應(yīng)用于評(píng)估信道質(zhì)量的研究尚處于起步階段，有限的研究也僅基于輔助數(shù)據(jù)符號(hào)的EVM（DA-EVM, data-aided error vector magnitude）的測(cè)試與計(jì)算[7～9]，并沒(méi)有從理論上建立衰落信道下EVM的數(shù)學(xué)模型，無(wú)法推廣到更為一般的κ?μ陰影衰落信道中；文獻(xiàn)[10]利用SNR作為中間變量，推導(dǎo)了DA-EVM在基于MRC傳輸模型下κ?μ陰影衰落信道的理論表達(dá)式，并在此基礎(chǔ)上進(jìn)行退化，給出了幾種典型信道下的DA-EVM閉合式，文獻(xiàn)[10]首次建立了利用DA-EVM分析κ?μ陰影衰落信道的理論體系架構(gòu)，但由于輔助數(shù)據(jù)固定間隔帶來(lái)的非實(shí)時(shí)統(tǒng)計(jì)誤差，文獻(xiàn)[10]中DA-EVM的解析式不能有效地應(yīng)用于κ?μ陰影衰落信道下的快時(shí)變場(chǎng)景。針對(duì)上述問(wèn)題，并考慮到實(shí)際通信系統(tǒng)多采用非輔助數(shù)據(jù)接收，有學(xué)者提出采用非輔助數(shù)據(jù)符號(hào)的 EVM（NDA-EVM,nondata-aided error vector magnitude）對(duì)衰落信道進(jìn)行分析[11]。NDA-EVM有以下優(yōu)點(diǎn)：1)NDA-EVM對(duì)于無(wú)線信道衰落極為敏感，衰落引起接收符號(hào)的細(xì)微變化即會(huì)引起NDA-EVM較大的波動(dòng)；2)不同于數(shù)據(jù)輔助的SNR和EVM估計(jì)，NDA-EVM估計(jì)不需要對(duì)比譯碼后的輔助數(shù)據(jù)，這樣即使在數(shù)據(jù)傳輸失敗的場(chǎng)景下，依然可以獲得NDA-EVM信息，并據(jù)此預(yù)測(cè)出當(dāng)前信道條件下通信系統(tǒng)可能達(dá)到的性能（如誤符號(hào)率和吞吐量）[12]。目前，衰落信道下的NDA-EVM理論分析僅針對(duì)某些典型信道，如文獻(xiàn)[11]給出了NDA-EVM在Reyleigh信道下的計(jì)算模型，測(cè)試結(jié)果表明理論值與實(shí)際測(cè)試值有很高的一致性，可對(duì)Reyleigh衰落信道下系統(tǒng)的性能進(jìn)行有效預(yù)測(cè)，然而文獻(xiàn)[11]并未將NDA-EVM對(duì)典型衰落信道表達(dá)式推廣至更為一般的κ?μ陰影衰落信道，其難點(diǎn)在于NDA-EVM對(duì)衰落信道定量分析需要給出閉合的解析式，而NDA-EVM在衰落信道下的建模具有很強(qiáng)的復(fù)雜性；同時(shí)NDA-EVM對(duì)κ?μ陰影衰落信道解析式也需要建立NDA-EVM與κ?μ分布關(guān)系，但此關(guān)系迄今依然是一個(gè)公開(kāi)的問(wèn)題，尚未有明確的解答。

據(jù)此，本文給出了SISO系統(tǒng)中利用NDA-EVM分析κ?μ陰影衰落信道的理論方法。以信道的衰落因子為中間變量，建立了κ?μ陰影衰落信道與NDA-EVM的聯(lián)系；通過(guò)最大似然準(zhǔn)則推導(dǎo)了MQAM符號(hào)在衰落信道下NDA-EVM的閉合式；并在上述基礎(chǔ)上給出NDA-EVM在κ?μ陰影衰落信道下的理論下限，通過(guò)靈敏度分析進(jìn)一步研究了信道參數(shù)對(duì)所推導(dǎo)下限的影響程度。經(jīng)過(guò)仿真模擬，表明推導(dǎo)的下限值與理論值一致性較好，特別在低信噪比下有緊下界，且下限值對(duì)信道變化非常敏感，可為系統(tǒng)接收性能的準(zhǔn)確預(yù)測(cè)提供理論支撐。

2 NDA-EVM在κ?μ陰影衰落信道的理論界限

κ?μ陰影衰落信道下NDA-EVM理論分析的基本思路是以MQAM信號(hào)在單輸入單輸出（SISO,single-input single-output）系統(tǒng)傳輸為系統(tǒng)背景，推導(dǎo)κ?μ陰影衰落信道下衰落因子的概率密度函數(shù)以及NDA-EVM的計(jì)算模型，以信道衰落因子為中間變量建立NDA-EVM與κ?μ陰影衰落信道之間的聯(lián)系，由此推導(dǎo)出NDA-EVM的理論界限。

2.1 信道衰落因子在κ?μ陰影衰落信道下的概率密度函數(shù)

在SISO系統(tǒng)中，MQAM信號(hào)在κ?μ陰影衰落信道下的模型可表示為

其中，n均值為0、功率譜密度為的復(fù)高斯隨機(jī)過(guò)程，；信道歸一化衰落因子為α，信號(hào)包絡(luò)能量的概率分布函數(shù)[13]為

其中，1F1(·)為Kummer超流函數(shù)。由文獻(xiàn)[13]的結(jié)論和SISO系統(tǒng)單天線接收的特性，式(2)可以表示為

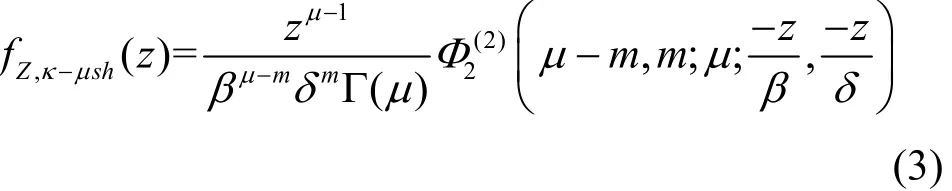
其中，為雙變量合流超幾何函數(shù)。由于2z=α，由式(3)可以進(jìn)一步推出衰落因子α在κ?μ陰影衰落信道下的概率密度函數(shù)為

2.2 MQAM信號(hào)的NDA-EVM閉合解

NDA-EVM反映了接收符號(hào)與發(fā)送符號(hào)星座點(diǎn)的均方誤差，在實(shí)際的系統(tǒng)中，收發(fā)信機(jī)的非理想狀態(tài)（如功放工作在非線性區(qū)、載波泄露、I/Q不平衡等）和無(wú)線信道衰落是影響系統(tǒng)性能的2個(gè)典型方面，均會(huì)對(duì)NDA-EVM的評(píng)估產(chǎn)生影響。實(shí)際的通信系統(tǒng)，由于收發(fā)信機(jī)的工作狀態(tài)確定，所以設(shè)備的非理想狀態(tài)對(duì)NDA-EVM的影響是固定的，這種影響可采用射頻線纜連接收發(fā)信機(jī)的方式，通過(guò)儀器準(zhǔn)確地度量出來(lái)。而信道的隨機(jī)特性，信道衰落對(duì)NDA-EVM的影響不是固定的，是隨信道參數(shù)改變而變化的。

接收端NDA-EVM的誤差評(píng)估是收發(fā)信機(jī)的非理想狀態(tài)和信道衰落這 2個(gè)方面影響的“線性疊加”，由于這 2個(gè)方面的因素彼此獨(dú)立，通過(guò)測(cè)量得出設(shè)備對(duì)NDA-EVM的影響后，就可以得出信道變化對(duì)NDA-EVM的影響。利用接收符號(hào)來(lái)計(jì)算NDA-EVM，由于接收符號(hào)受設(shè)備非理想和信道衰落的影響，估計(jì)出的NDA-EVM也反映了這2類(lèi)影響因素的疊加，在除去測(cè)量得到設(shè)備非理想狀態(tài)下的NDA-EVM，就可以得出信道對(duì)NDA-EVM的影響。基于此，為了方便分析，本文假設(shè)收發(fā)信機(jī)是理想狀態(tài)，NDA-EVM僅受信道衰落影響，通過(guò)NDA-EVM來(lái)評(píng)估信道質(zhì)量[11]，它可表示為

其中，y[i]是第i個(gè)接收符號(hào)，是由接收符號(hào)通過(guò)最大似然準(zhǔn)則估計(jì)出的發(fā)送符號(hào)，為不失一般性，設(shè)P0=1。發(fā)送符號(hào)Si為M階的MQAM符號(hào)，可表示為

其中，因?yàn)镸QAM符號(hào)實(shí)部和虛部具有對(duì)稱性，下文僅考慮實(shí)部用下標(biāo)R表示，且省略收/發(fā)符號(hào)的索引號(hào)i，簡(jiǎn)化式(5)為為歸一化幅度

由式(1)可知，接收符號(hào)的實(shí)部yR的條件概率密度函數(shù)可表示為

其中，?(·)為標(biāo)準(zhǔn)正態(tài)分布的概率密度函數(shù)。在最大似然準(zhǔn)則下，由接收符號(hào)yR估計(jì)出發(fā)送符號(hào)為的概率為

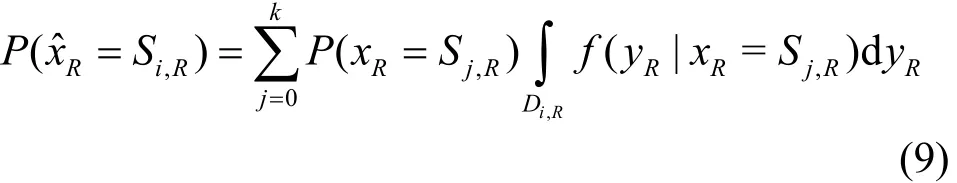
其中，Di,R為發(fā)送符號(hào)Si,R的判決域

由于發(fā)送符號(hào)等概率出現(xiàn)，可由條件概率求出

將式(9)和式(11)代入式(7)，可得

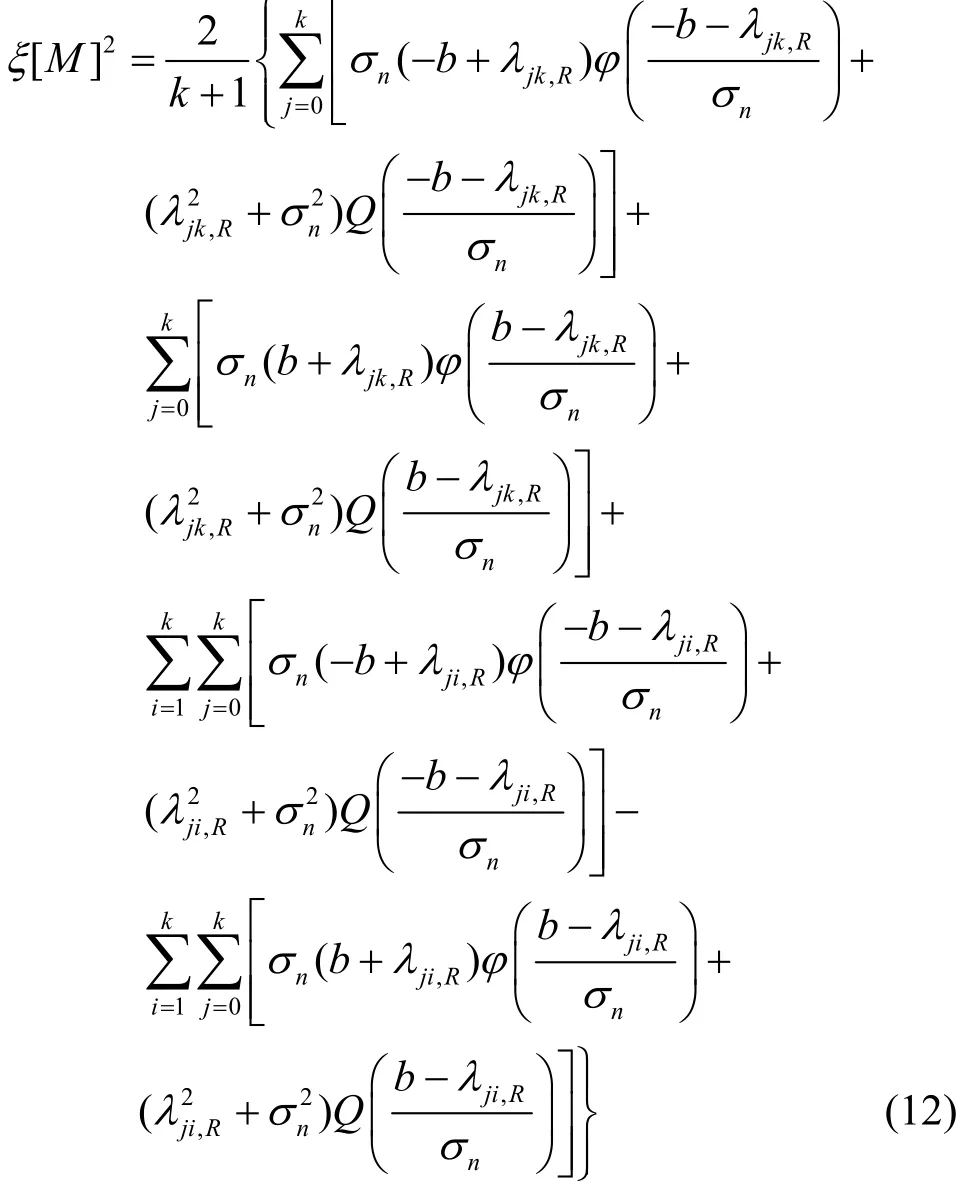
其中，Q(·)為互補(bǔ)累計(jì)分布函數(shù)，λji,R=?Si,R+αRSj,R。至此，式(12)給出了衰落信道下各調(diào)制階數(shù)NDA-EVM的統(tǒng)一計(jì)算模型。式(12)表示當(dāng)調(diào)制階數(shù)為M的星座點(diǎn)被接收端依概率判決在Di,R域中3個(gè)區(qū)域時(shí)，每個(gè)區(qū)域中對(duì)應(yīng)的EVM值的累加。

根據(jù)其物理意義，NDA-EVM可分為2個(gè)部分，第一部分為式(12)右邊中第一和第二個(gè)累加項(xiàng)，表示Di,R域中2個(gè)邊緣區(qū)域D0,R和Dk,R的EVM值，第二部分為后面2個(gè)累加項(xiàng)的差，表示1 ≤i≤k?1的中間區(qū)域Di,R的EVM值。由于第二部分恒為正值，且遠(yuǎn)小于第一部分的EVM值。由式(12)可以表示為

考慮到μjk,R=b[α(j?k) + (αj?k)]＜ 0和Q(x)的單調(diào)遞減性，可得。又由于

同理，，式(13)可以進(jìn)一步放縮為

根 據(jù) Cauchy–Schwarz–Buniakowsky 不 等 式[14]，令bk=1，可得，由此，式(14)可表示為

其中，，化簡(jiǎn)式(15)最終可得出NDA-EVM的下限為

2.3 κ?μ陰影衰落信道下NDA-EVM的下限

κ?μ陰影衰落信道下NDA-EVM的下限表示在該信道下NDA-EVM估計(jì)所能達(dá)到的最小值，它反映出當(dāng)前信道環(huán)境MQAM信號(hào)在最佳接收時(shí)的星座點(diǎn)偏移，由此可以推算出在此信道狀態(tài)下系統(tǒng)可達(dá)到的最優(yōu)性能（如自適應(yīng)調(diào)制系統(tǒng)在當(dāng)前信道條件下的最高調(diào)制階數(shù)以及系統(tǒng)可以達(dá)到的最低誤碼率），NDA-EVM下限可為無(wú)線傳輸系統(tǒng)的設(shè)計(jì)提供一個(gè)量化指標(biāo)。

上文推導(dǎo)了衰落因子α在κ?μ陰影衰落信道下的概率密度函數(shù)，以及NDA-EVM在衰落信道下的解析式，以衰落因子α為中間變量，可以建立NDA-EVM在κ?μ陰影衰落信道下的模型。它可由κ?μ陰影衰落信道下的每一個(gè)瞬間衰落對(duì)應(yīng)的NDA-EVM在該衰落因子α概率分布上的加權(quán)來(lái)量化。即

可以看出式(17)下限可由NDA-EVM的下限決定，由此將式(4)、式(16)代入式(17)可得2

令，將式(18)做積分變量替換后，可以表示為

其中，。在滿足的條件下，2(k)p1α≥ 。

由此，式(19)可進(jìn)一步化簡(jiǎn)為

利用文獻(xiàn)[15]中的性質(zhì)

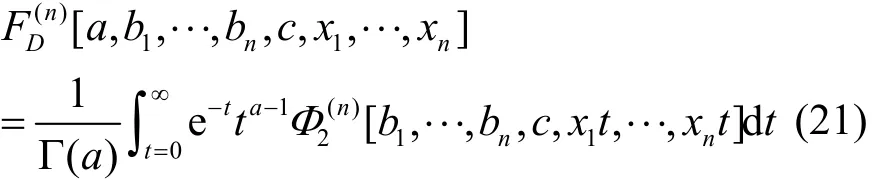
對(duì)式(20)進(jìn)行化簡(jiǎn)，最終得到不同調(diào)制階數(shù)的

NDA-EVM在κ?μ陰影衰落信道的下限成立的條件，需滿足0＜p＜μ。由此，式(22)的p最優(yōu)值p?可通過(guò)對(duì)p進(jìn)行優(yōu)化求取。

值得注意的是，為了滿足

通過(guò)數(shù)值搜索的方法，不同調(diào)制階數(shù)的NDA-EVM在κ?μ陰影衰落信道的最緊下限可由最優(yōu)的p?值確定。

2.4 NDA-EVM下限在幾種典型信道下的退化

κ?μ陰影衰落信道可以退化為幾種典型的信道，如Rice信道和Nakagami-m信道等，由此也可以得到NDA-EVM在這幾種典型信道下的下限。

1) Rice信道

當(dāng)μ=1時(shí)，κ?μ陰影衰落信道可以化簡(jiǎn)為Rice信道，此時(shí)的κ即為萊斯因子。由此可得

在Rice信道的下限可以簡(jiǎn)化為

p最優(yōu)值p?可表示為

為驗(yàn)證NDA-EVM及其下限在Rice信道的有效性，將由式(12)得到的NDA-EVM值、式(24)得到的下限值以及LTE-A標(biāo)準(zhǔn)3GPP TS 36.101定義的EVM值進(jìn)行對(duì)比[16]。Rice信道下( 1, 10μ=κ= )，當(dāng)SNR=0 dB，α=0.8時(shí)，三者對(duì)比如表1所示。

表1 在Rice信道下NDA-EVM及其下限與LTE-A標(biāo)準(zhǔn)EVM典型值的對(duì)比

由表1可以看出，當(dāng)κ?μ陰影衰落信道退化為 Rice信道，由本文算法求取的NDA-EVM與 LTE-A標(biāo)準(zhǔn)下的典型值較為接近，且各階調(diào)制模式下的NDA-EVM下限值與典型值的差異均小于8%。

2) Nakagami-m信道

當(dāng)κ→0時(shí)，κ?μ陰影衰落信道可以化簡(jiǎn)為Nakagami-m信道。由此可得。將其代入式(22)，可化簡(jiǎn)為

由文獻(xiàn)[15]可知

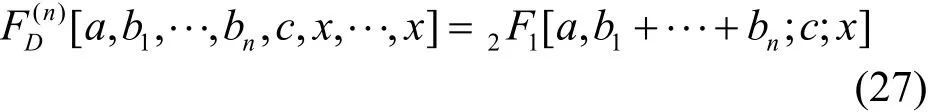
式(26)可進(jìn)一步化簡(jiǎn)，得到NDA-EVM在Nakagami-m信道的下限值為

其中，p最優(yōu)值p?可表示為

同理，為驗(yàn)證所推下限的有效性，在Nakagami-m信道(κ= 0.01,μ= 1時(shí))下，對(duì) LTE-A標(biāo)準(zhǔn)下的EVM典型值、NDA-EVM以及其下限值進(jìn)行對(duì)比。當(dāng)SNR=0 dB，α=0.9時(shí)，三者對(duì)比如表2所示。

表2 在Nakagami-m信道下NDA-EVM及其下限與LTE-A標(biāo)準(zhǔn)EVM典型值的對(duì)比

由表2可以看出，在Nakagami-m信道，NDAEVM與LTE-A標(biāo)準(zhǔn)下的典型值較為接近，且各階調(diào)制模式下的NDA-EVM下限值與典型值的差異均小于10%。

綜上可知，在κ?μ陰影衰落信道退化為 Rice和Nakagami-m典型信道時(shí)，NDA-EVM與LTE-A標(biāo)準(zhǔn)下的典型值一致，NDA-EVM的下限值放縮誤差小于 10%，可以對(duì)κ?μ陰影衰落信道進(jìn)行有效的評(píng)估。

3 NDA-EVM特性的理論分析

3.1 下限的參數(shù)靈敏度分析

由式(22)可知，NDA-EVM下限受參數(shù)k、μ、κ的影響。參數(shù)靈敏度反映了信道參數(shù)κ、μ、調(diào)制階數(shù)對(duì)NDA-EVM下限的影響程度，通過(guò)靈敏度分析可發(fā)現(xiàn)NDA-EVM下限對(duì)哪些參數(shù)變化敏感，從而為分析不同信道下NDA-EVM的性能提供理論支撐。

第二，壟斷性國(guó)有企業(yè)的分類(lèi)重組改造是國(guó)有企業(yè)混合所有制改革的必要條件。《關(guān)于國(guó)有企業(yè)功能界定與分類(lèi)的指導(dǎo)意見(jiàn)》界定了三類(lèi)國(guó)有企業(yè)，即主業(yè)處于充分競(jìng)爭(zhēng)行業(yè)和領(lǐng)域的商業(yè)類(lèi)國(guó)有企業(yè)；主業(yè)處于關(guān)系國(guó)家安全、國(guó)民經(jīng)濟(jì)命脈的重要行業(yè)和關(guān)鍵領(lǐng)域，主要承擔(dān)重大專(zhuān)項(xiàng)任務(wù)的商業(yè)類(lèi)國(guó)有企業(yè)；處于自然壟斷行業(yè)的國(guó)有企業(yè)。這三類(lèi)企業(yè)的混合所有制改革方向、路徑和目標(biāo)截然不同，需要分類(lèi)處置。但是目前我們的國(guó)有企業(yè)，尤其是大型央企大多是三種業(yè)務(wù)兼而有之，甚至部分央企還承擔(dān)社會(huì)公益服務(wù)，綜合性業(yè)務(wù)采取一種混合所有制改革路徑顯然不適宜。因此，需要采取剝離、重組、整合、改造等手段，予以分類(lèi)處置和歸一化處理[3-5]。

為了量化單參數(shù)變化對(duì)下限值的影響程度，NDA-EVM下限的靈敏度分析采用各參數(shù)的靈敏度系數(shù)進(jìn)行定量評(píng)估。根據(jù)文獻(xiàn)[17]對(duì)靈敏度的定義，變量參數(shù)xi對(duì)系統(tǒng)y(x)的靈敏度系數(shù)Sxi可表示為

可以得到參數(shù)k、μ、κ的靈敏度系數(shù)，如表3所示。

圖1分別給出了調(diào)制參數(shù)k、信道參數(shù)μ、κ的靈敏度分析曲線。它們反映了其中任意一個(gè)變量在其余2個(gè)變量固定時(shí)對(duì)NDA-EVM下限的影響程度。

從圖1可以看出以下3點(diǎn)。1)，即調(diào)制階數(shù)對(duì)NDA-EVM下限值的影響最大，信道參數(shù)μ影響次之，信道參數(shù)κ影響最小。2)Sk、Sμ、Sκ均為負(fù)值，調(diào)制參數(shù)k、信道參數(shù)μ、κ均與NDA-EVM下限負(fù)相關(guān)，即任一參數(shù)變大，NDA-EVM在κ?μ陰影衰落信道的下限均會(huì)減小。3) 調(diào)制參數(shù)k、信道參數(shù)μ、κ的值由小變大，其靈敏度系數(shù)的絕對(duì)值由大變小并接近 0，表明隨著3種參數(shù)值變大，NDA-EVM下限趨于穩(wěn)定，最終收斂。

表3 NDA-EVM下限的參數(shù)靈敏度

圖1 NDA-EVM下限的參數(shù)靈敏度分析

圖1 NDA-EVM下限的參數(shù)靈敏度分析（續(xù)）

3.2 低信噪比的緊下界

在求取NDA-EVM下限時(shí)，對(duì)NDA-EVM的閉合式進(jìn)行放縮，放縮誤差的主要來(lái)源于式(12)對(duì)后2項(xiàng)中“2個(gè)累加項(xiàng)的差”的處理，下面分析低信噪比下的放縮誤差，記誤差項(xiàng)為

由此可知，在低信噪比條件下，誤差項(xiàng)趨近于0，其物理意義是：在信噪比很低的條件下，接收端的星座符號(hào)大量的偏離理想星座點(diǎn)，大概率的分布在Di,R域中2個(gè)邊緣區(qū)域D0,R和Dk,R，分布于中間區(qū)域Di,R的概率很小，計(jì)算NDA-EVM時(shí)可以將其忽略掉。

圖2給出了低信噪比情況下ε的變化情況，由圖 2可見(jiàn)，ε在低信噪比區(qū)，各個(gè)調(diào)制階數(shù)的NDA-EVM均趨近于0，與理論的分析吻合。

由于在低信噪比下，MQAM信號(hào)的NDA-EVM有緊下界，所以由式(16)推導(dǎo)出的NDA-EVM在κ?μ陰影衰落信道的下界在低信噪比區(qū)依然是緊下界。

3.3 NDA-EVM在κ?μ陰影衰落信道下的RMSE

為了驗(yàn)證NDA-EVM評(píng)估κ?μ陰影衰落信道的準(zhǔn)確性，本節(jié)利用最小均方誤差（RMSE, root mean square error）對(duì)比分析了NDA-EVM、DA-EVM和DA-SNR這3種信道評(píng)估參量。RMSE反映了信道估計(jì)值與真實(shí)值之間的差異，它定量給出了NDA-EVM、DA-EVM和DA-SNR的估計(jì)偏差。由于本文假設(shè)收發(fā)信機(jī)理想狀態(tài)，在不考慮設(shè)備誤差的情況下，RMSE的物理意義是3種信道質(zhì)量評(píng)估參量受無(wú)線信道影響時(shí)的估計(jì)偏差。RMSE越小，表明信道質(zhì)量評(píng)估值越接近實(shí)際值，越能準(zhǔn)確地表征信道質(zhì)量。由于實(shí)際信道具有隨機(jī)特性，實(shí)際的測(cè)試也只能反映某一時(shí)刻特定狀態(tài)的信道特征，無(wú)法反映所有參數(shù)變化對(duì)信道評(píng)估參量的影響，所以本文采用蒙特卡洛方法對(duì)不同的信道參數(shù)逐一掃描，模擬信道變化時(shí)NDA-EVM、DA-EVM和DA-SNR的評(píng)估準(zhǔn)確性。為模擬信道的隨機(jī)特性，將大量發(fā)送數(shù)據(jù)通過(guò)不同信道參數(shù)的κ?μ陰影衰落信道，并記錄不同信道參數(shù)改變下，由式(12)估計(jì)算出的NDA-EVM值（記為Eξ），同時(shí)接收端利用蒙特卡洛算法，比較接收星座點(diǎn)與理想星座點(diǎn)的偏差，進(jìn)行NDA-EVM測(cè)算，將其作為NDA-EVM在κ?μ陰影衰落信道下的真實(shí)值（記為ξR）。經(jīng)過(guò) 105次測(cè)算后，由，可以計(jì)算出NDA-EVM的RMSE。同理，可得出DA-EVM和DA-SNR的RMSE。

圖3和圖4給出了NDA-EVM與傳統(tǒng)的信道質(zhì)量評(píng)估量（DA-SNR和DA-EVM）在κ?μ陰影衰落信道下估值的均方誤差曲線。其中，輔助數(shù)據(jù)的分布為每100個(gè)數(shù)據(jù)符號(hào)插入1個(gè)已知序列的輔助數(shù)據(jù)符號(hào)。由圖3和圖4可知：隨著信道參數(shù)μ的減小，3種估計(jì)量的RMSE均增加，但NDA-EVM估計(jì)值與真實(shí)值更為接近，RMSE明顯低于傳統(tǒng)評(píng)估量，且μ值越小，NDA-EVM與對(duì)比統(tǒng)計(jì)量在RMSE上的差距越明顯，這是因?yàn)閰?shù)μ越小，信道衰落加劇引起的接收信號(hào)畸變?cè)絿?yán)重[18]，DA-EVM和DA-SNR估計(jì)速率受輔助數(shù)據(jù)固定間隔影響無(wú)法準(zhǔn)確反映信道的快速變化；同理，隨著信道參數(shù)κ的減小，表明衰落造成的信號(hào)能量耗散增加[18]，接收信號(hào)惡化，但NDA-EVM估計(jì)同樣有最小的RMSE。說(shuō)明NDA-EVM對(duì)κ?μ陰影衰落信道質(zhì)量的評(píng)估更為準(zhǔn)確，較傳統(tǒng)評(píng)估量也更為有效。

圖3 μ=1, κ變化時(shí)3種評(píng)估參量的RMSE

圖4 κ=1, μ變化時(shí)3種評(píng)估參量的RMSE

可以看出，NDA-EVM估計(jì)在不同的信道環(huán)境下均有比DA-EVM和DA-SNR低的估計(jì)誤差，其根本原因在于NDA-EVM不受輔助數(shù)據(jù)間隔的影響，信道質(zhì)量評(píng)估實(shí)時(shí)性好。在實(shí)際的應(yīng)用中，由于DA-EVM和DA-SNR是依靠輔助數(shù)據(jù)（如導(dǎo)頻、前導(dǎo)）來(lái)完成信道質(zhì)量的測(cè)算，輔助數(shù)據(jù)的間隔決定了信道質(zhì)量評(píng)估的速度，DA-EVM和DA-SNR顯然無(wú)法跟蹤信道的變化。特別是應(yīng)用到數(shù)據(jù)分組或自適應(yīng)調(diào)制這類(lèi)對(duì)實(shí)時(shí)性要求較高的系統(tǒng)中，系統(tǒng)需要對(duì)信道質(zhì)量實(shí)時(shí)評(píng)估以調(diào)整傳輸參數(shù)，以DA-EVM和DA-SNR為信道質(zhì)量評(píng)估參量就會(huì)因?yàn)閷?shí)時(shí)性差導(dǎo)致傳輸參數(shù)的選擇錯(cuò)誤，影響系統(tǒng)性能。總之，NDA-EVM在信道質(zhì)量估計(jì)的實(shí)時(shí)性和準(zhǔn)確性上要優(yōu)于DA-EVM和DA-SNR，可為實(shí)際通信系統(tǒng)中自適應(yīng)調(diào)制門(mén)限的精確選取、時(shí)變信道下的傳輸策略優(yōu)化以及系統(tǒng)接收性能的準(zhǔn)確預(yù)測(cè)提供理論參考。

4 κ?μ陰影衰落信道下NDA-EVM的性能仿真

為了對(duì)NDA-EVM在κ?μ陰影衰落信道下可以達(dá)到的性能界限進(jìn)行分析，本節(jié)采用蒙特卡洛法進(jìn)行仿真實(shí)驗(yàn)。仿真模擬了 SISO系統(tǒng)，對(duì)通過(guò)κ?μ陰影衰落信道的MQAM信號(hào)進(jìn)行NDA-EVM測(cè)算，將經(jīng)過(guò)105次測(cè)算的NDA-EVM算術(shù)平均后作為其在κ?μ陰影衰落信道下的理論值，通過(guò)與文本估計(jì)值進(jìn)行仿真對(duì)比，分析不同信道參數(shù)下NDA-EVM的性能。

4.1 不同調(diào)制階數(shù)MQAM符號(hào)的NDA-EVM下限

圖5給出了在κ?μ陰影衰落信道下NDA-EVM下限在不同調(diào)制階數(shù)下的性能。信道參數(shù)為κ= 0.85，μ=0.55，在此信道參數(shù)下通過(guò)數(shù)值搜索確定出各調(diào)制階數(shù)NDA-EVM下限值的最優(yōu)p*，其中QAM(p*= 0.28)，16QAM(p*= 0.26)，64QAM(p*= 0.2025)。由圖5可知：1) 低信噪比下NDA-EVM在κ?μ陰影衰落信道的下限接近理論值，這種特性在第3.2節(jié)中進(jìn)行了詳細(xì)的分析。值得注意的是，當(dāng)信噪比不斷增加時(shí)，NDA-EVM的下限值不斷減小直至收斂；2)NDA-EVM在κ?μ陰影衰落信道的下限值受調(diào)制階數(shù)的影響較大，調(diào)制階數(shù)越高，NDA-EVM下限越低，這種現(xiàn)象可由調(diào)制階數(shù)對(duì)NDA-EVM下限的靈敏度特性得出解釋。

圖5 不同調(diào)制階數(shù)MQAM符號(hào)在κ?μ陰影衰落信道下的NDA-EVM下限

4.2 不同信道參數(shù)μ的NDA-EVM下限

圖6比較了QAM信號(hào)在μ參數(shù)變化時(shí)NDA-EVM下限與理論值的性能差異。由圖6可知：1) 低信噪比使NDA-EVM下限值逼近于理論值，隨著信噪比增加NDA-EVM下限最終收斂；2) 隨著信道參數(shù)μ的增加，NDA-EVM下限值不斷降低，這是由于參數(shù)μ表示了衰落信道的直視徑能量的集中程度[2]，參數(shù)μ越大，直視徑能量越集中，NDA-EVM有較低的下限值。同時(shí)，由靈敏度分析可知，參數(shù)μ對(duì)下限值的影響較大，較小的μ變化將造成NDA-EVM下限的較大波動(dòng)。

圖6 不同信道參數(shù)μ的NDA-EVM下限

4.3 不同信道參數(shù)κ的NDA-EVM下限

圖7比較了QAM信號(hào)在κ參數(shù)變化時(shí)NDAEVM下限與理論值的性能差異。

圖7 不同信道參數(shù)κ的NDA-EVM下限

由圖7可知：1) 與前文分析一樣，在不同信道參數(shù)κ的衰落信道中，NDA-EVM下限與理論值在低信噪比下有較小差距，隨著信噪比增加NDA-EVM下限最終收斂；2) 隨著信道參數(shù)κ的增加，NDA-EVM下限值不斷降低，這是由于參數(shù)κ表示了信道衰落下接收端信號(hào)能量的集中程度[2]，參數(shù)κ越大，衰落造成的能量耗散越小，因此NDA-EVM有較低的下限值。同時(shí)，由參數(shù)的靈敏度分析可知，相較其他參數(shù)，κ的變化對(duì)NDA-EVM下限的影響最小。

5 結(jié)束語(yǔ)

本文提出一種基于NDA-EVM對(duì)κ?μ陰影衰落信道進(jìn)行理論分析的方法。通過(guò)最大似然準(zhǔn)則建立了衰落信道下NDA-EVM統(tǒng)一的計(jì)算模型；并以衰落因子為中間變量，建立了NDA-EVM與κ?μ分布的聯(lián)系，據(jù)此推導(dǎo)了NDA-EVM在κ?μ陰影衰落信道的理論表達(dá)式，給出了NDA-EVM在κ?μ陰影衰落信道可能達(dá)到的理論下限，并化簡(jiǎn)了理論下限在幾種典型信道（Rice信道和Nakagami-m信道）下的退化表達(dá)式。進(jìn)一步地，對(duì)所推導(dǎo)的NDA-EVM下限進(jìn)行參數(shù)靈敏度、緊下界以及信道評(píng)估參量的RMSE對(duì)比分析，并通過(guò)仿真模擬NDA-EVM在κ?μ陰影衰落信道下的性能。結(jié)果表明：1) 相較傳統(tǒng)的DA-SNR和DA-EVM，NDA-EVM對(duì)κ?μ陰影衰落信道的評(píng)估具有更小的RMSE值，評(píng)估結(jié)果更為準(zhǔn)確有效；2) 推導(dǎo)的NDA-EVM下限在低SNR區(qū)域更接近理論值；3)NDA-EVM在κ?μ陰影衰落信道的理論下限受到調(diào)制階數(shù)、參數(shù)κ和μ的影響，其中受調(diào)制階數(shù)影響程度最大，參數(shù)μ次之，

參數(shù)κ最小；4) 理論下限均與調(diào)制階數(shù)、參數(shù)κ和μ負(fù)相關(guān)變化，即理論下限均隨著參數(shù)的增大而降低。簡(jiǎn)言之，NDA-EVM在κ?μ陰影衰落信道定量分析具有廣泛的理論意義和工程應(yīng)用價(jià)值，可為自適應(yīng)調(diào)制門(mén)限的精確選取、時(shí)變信道下傳輸策略的優(yōu)化以及系統(tǒng)接收性能的準(zhǔn)確預(yù)測(cè)提供理論參考。

[1] YACOUB M D. Theκ-μdistribution∶ a general fading distribution[C]//Vehicular Technology Conference, 2001∶ 1427-1431.

[2] YACOUB M D. Theκ-μdistribution and theη-μdistribution[J]. IEEE Antennas and Propagation Magazine, 2007, 49(1)∶ 68-81.

[3] HANZO L, NG S X, WEBB W T, et al. Quadrature amplitude modulation∶ from basics to adaptive trellis-coded, turbo-equalised and space-time coded OFDM, CDMA and MC-CDMA systems[M]. IEEE Press-John Wiley, 2004.

[4] SHAFIK R A, RAHMAN M S, ISLAM A H M R, et al. On the error vector magnitude as a performance metric and comparative analysis[C]// ICET'06. International Conference on Emerging Technologies,2006∶ 27-31.

[5] 周峰, 張睿, 高攸綱, 等. 五種失真因素綜合作用下的 EVM[J]. 電子學(xué)報(bào), 2012, 40(3)∶ 607-610.ZHOU F, ZHANG R, GAO Y G, et al. Error vector magnitude by five distortion factors[J]. Acta Electronica Sinica, 2012, 40(3)∶ 607-610.

[6] 游長(zhǎng)江, 朱曉維, 柳靖, 等. 基于射頻前端的動(dòng)態(tài)頻譜共享無(wú)線通信系統(tǒng)工作信道選擇分析[J]. 通信學(xué)報(bào), 2011, 32(4)∶ 147-152.YOU C J, ZHU X W, LIU J. Analysis of operational channel selection of dynamic spectrum sharing wireless communication system based on RF front-end[J]. Journal on Communications, 2011, 32(4)∶ 147-152.

[7] CHOUITEM R. EVM based AMC for an OFDM system[C]//Wireless Telecommunications Symposium (WTS), 2010. IEEE, 2010∶ 1-5.

[8] LIU R, LI Y, CHEN H, et al. EVM estimation by analyzing transmitter imperfections mathematically and graphically[J]. Analog Integrated Circuits and Signal Processing, 2006, 48(3)∶ 257-262.

[9] GEORGIADIS A. Gain, phase imbalance, and phase noise effects on error vector magnitude[J]. IEEE Transactions on Vehicular Technology,2004, 53(2)∶ 443-449.

[10] THOMAS V A, KUMAR S, KALYANI S, et al. Error vector magnitude analysis of fading SIMO channels relying on MRC reception[J].IEEE Transactions on Communications, 2016, 64(4)∶ 1786-1797.

[11] MAHMOUD H A, ARSLAN H. Error vector magnitude to SNR conversion for nondata-aided receivers[J]. IEEE Transactions on Wireless Communications, 2009, 8(5)∶ 2694-2704.

[12] SEN S, SANTHAPURI N, CHOUDHURY R R, et al. AccuRate∶constellation based rate estimation in wireless networks[C]//NSDI.2010∶ 175-190.

[13] PARIS J F. Statistical characterization ofκ-μshadowed fading[J].IEEE Transactions on Vehicular Technology, 2014, 63(2)∶ 518-526.

[14] ALAN J, DANIEL Z. Table of integrals, series and products (7th ed)[M]. New York∶ Academic, 2007.

[15] EXTON H. Multiple hypergeometric functions and applications[M].Halsted Press, Ellis Horwood, 1976.

[16] 3GPP TS 36.101. User Equipment (UE) radio transmission and reception[S]. 2010.

[17] SALTELLI A, CHAN K, SCOTT E M. Sensitivity analysis[M]. New York∶ Wiley, 2000.

[18] COTTON S L. Second-order statistics ofκ-μshadowed fading channels[J]. IEEE Transactions on Vehicular Technology, 2016, 65(10)∶8715-8720.