基于子結構和模式重復的地鐵車輛座椅支架拓撲優化

李婭娜 于海玲 邱廣宇

摘要：

針對地鐵車輛座椅模型加載范圍廣和座椅支架結構對稱的特點，在進行地鐵車輛座椅支架拓撲優化時，采用SIMP理論建立數學模型，同時引進子結構和模式重復方法，優化得到符合設計要求的結構。對比結果認為：優化后的地鐵車輛座椅支架質量減輕49%，地鐵車輛整體的強度性能增強，可達到地鐵車輛座椅支架輕量化的目標。

關鍵詞：

拓撲優化； 子結構法； 模式重復； 地鐵車輛； 座椅支架； 柔順性

中圖分類號： U270.38

文獻標志碼： B

Topology optimization of metro vehicle seat support

based on substructure and mode repetition

LI Yana， YU Hailing， QIU Guangyu

（

College of Traffic and Transportation Engineering， Dalian Jiaotong University， Dalian 116028， Liaoning， China）

Abstract：

In view of the wide loading range of the metro vehicle seat model and the seat support structure symmetry features， the topology optimization of the metro vehicle seat support is carried out. The mathematical model of topology optimization is built by SIMP theory. The substructure method and the mode repetition are presented to optimize the structure， which meets the requirements of the design. The comparison results show that the mass of the optimized metro vehicle seat support is reduced by 49%， and the whole strength of the metro vehicle is enhanced， which can meet the lightweight target of the metro vehicle seat bracket.

Key words：

topology optimization； substructure method； mode repetition； metro vehicle； seat support； flexibility

收稿日期： 2017-11-27

修回日期： 2017-12-13

作者簡介：

李婭娜（1977—），女，遼寧大連人，副教授，博士，研究方向為車輛結構設計與現代設計方法，（E-mail）lyn1977522@163.com

0 引 言

地鐵在中國的地位舉足輕重，低成本、輕量化設計是其發展的主要方向。[1]SIMP理論通過引入懲罰因子，在結構剛度和相對密度之間建立一種非線性關系。對于大型地鐵車輛結構，采用合適的拓撲優化技術和子結構技術，有利于地鐵車輛的輕量化發展。座椅支架是地鐵車輛座椅非常重要的組成部分，起到承載和傳遞各種力的作用，因此，研究如何減輕地鐵車輛座椅支架的質量非常必要。

目前，一些學者在拓撲優化設計方面進行很多研究。在汽車領域：吳仕賦[2]對汽車支架拓撲優化設計進行研究，提出優化設計方案并進行改進，使得機械結構和機械零部件質量減輕、結構可靠；楊天云等[3]對CAE在汽車座椅輕量化設計中的應用進行研究，以汽車座椅靠背為研究對象，運用密度法對汽車座椅骨架進行拓撲優化設計，最終達到座椅輕量化的目的；丁曉紅等[4]對結構拓撲優化過程中邊界條件的確定方法進行研究，提出通過逐步逼近使某型汽車前排座椅骨架的右側板拓撲形態逐步趨優的算法。在鐵路領域：王曉明等[5]對動車組行李架支座結構拓撲優化設計進行研究，主要對結構材料布局進行優化，并采用準則法對優化問題進行求解；聶春戈等[6]對高速轉向架軸箱轉臂結構拓撲優化設計進行研究，采用變密度法對高速轉向架軸箱轉臂進行輕量化設計，并與原方案進行對比分析驗證；高月華等[7]對基于子結構法的動車組設備艙支架進行優化設計，以設備艙支架結構為優化對象，優化后結構的剛度和強度均有所提高。在航空領域：吳中博等[8]對基于Optistruct的結構靜、動力拓撲優化設計進行研究，主要對平面薄板和三維連續體結構的靜力、動力以及靜動力特性聯合拓撲優化。在機械領域：高鵬飛等[9]對子結構法在活塞結構優化中的應用進行研究，通過子結構法和傳統有限元法的對比，得到最優設計方案。

本文對地鐵車輛座椅支架進行拓撲優化設計，考慮到支架結構復雜，在進行優化計算時，利用子結構法提高計算效率。此外，將模式重復方法引入到支架的拓撲優化計算中，使結構具有一致性，達到簡化制造工藝的目的。

1 地鐵車輛座椅結構有限元分析

1.1 結構模型

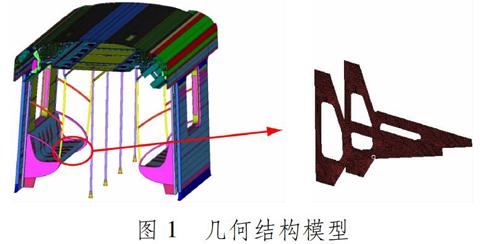
地鐵車輛座椅結構由7人座椅、擋風板扶手、側墻板、腰靠、中立柱扶手和車頂安裝型材組成，其中，7人座椅通過安裝支架和擋風板固定，其幾何結構模型見圖1。

圖 1 幾何結構模型

地鐵車輛座椅結構的擋風板扶手、中立柱扶手和腰靠結構模型以六面體單元為主，局部連接件由四面體單元構成。7人座椅、側墻板和車頂安裝型材有限元模型以任意四節點薄殼單元為主，三節點薄殼單元為輔。整個有限元模型的單元總數為2 073 704個、節點總數為2 279 619個。

1.2 載荷工況

地鐵車輛座椅結構的載荷工況分為以下3種：在水平扶手管、豎直扶手管上施加1 300 N/m均布力；在水平扶手管、豎直扶手管上施加900 N集中力；座椅承受100×7 kg的均布載荷。

1.3 計算結果

為考察地鐵車輛座椅結構的整體力學性能，需要對其整體結構進行靜強度分析。根據3種載荷工況的靜強度計算結果可知，整個結構的應力最大值均在許用范圍內。在豎直扶手管縱向位移最大處施加集中力，且在計算座椅面施加均布載荷時應力值最大。在該工況下，模型應力集中出現在座椅面上，其應力值為201.4 MPa（材料為06CR19NI10不銹鋼，許用應力為205.0 MPa），地鐵車輛座椅模型應力云圖見圖2。考慮座椅支架與座椅面的連接關系，為降低座椅面的應力集中，將座椅支架作為優化對象進行結構分析。

圖 2 模型應力云圖， MPa

2 基于Optistruct的拓撲優化

2.1 拓撲優化的原理

基于變密度法中的SIMP材料插值模型理論，采用Optistruct進行拓撲優化。拓撲優化技術是結構優化技術中存在實用價值且較先進的一項技術[10]，其能為設計者提供創新性的拓撲結構。與形狀和尺寸優化相比，拓撲優化結果可決定結構的形狀和力學性能。[11]把座椅支架作為拓撲優化對象，改變結構的受力方式，減少結構的應力集中，從而提高結構的可靠性，使座椅支架的性能達到期望的目標。

確定優化設計區域時，在不改變模型結構連接關系的前提下，用殼單元填充座椅支架的不封閉空間，使其成為封閉的設計空間（見圖3）。

圖 3 扶手部分結構模型拓撲優化區域

拓撲優化方法主要采用變密度法。設計變量為座椅支架的單元密度，在0～1范圍內連續取值。目標函數為地鐵車輛座椅結構的柔順性，并取其最小值。設置座椅支架優化區域的體積比約束為40%，并約束結構應力在許用應力205.0 MPa之內。

對地鐵車輛座椅結構建立基于SIMP拓撲優化理論的數學模型，該數學模型可表述為

x=x1，x2，…，xn

（1）

目標函數為

C（x）=

UT

KU=ni=1xPi

uTi

k0

ui

（2）

約束條件為

V1/V0≤r

σi≤[σ]

F=

KU

0

（3）

式中：xi（i=1，2，…，n）為地鐵車輛座椅支架的相對單元密度；C（x）為地鐵車輛座椅部分結構的總體柔順性；

U為地鐵車輛座椅支架的位移矩陣；

K為地鐵車輛座椅支架優化前的總剛度矩陣；P為懲罰因子，P>1，一般取P=3；

ui和

k0分別為單元位移矩陣和單元剛度矩陣；V1為地鐵車輛座椅支架結構設計區域優化后的有效體積；V0為地鐵車輛座椅支架結構設計區域的原始體積；r為地鐵車輛座椅支架優化區域的體積分數約束百分比；σi為結構的應力值；[σ]為結構的許用應力值；

F為地鐵車輛座椅支架的載荷矩陣；xmax和xmin分別為單元設計變量的上限和下限，分別取1.00和0.01。

2.2 子結構原理

直接對地鐵車輛座椅進行拓撲優化計算量非常大，適當運用子結構技術，可使最終求解方程組的自由度數量大大降低，因此，采用縮減系統自由度數量的方法提高地鐵車輛座椅結構的計算效率。

選擇地鐵車輛座椅局部作為拓撲優化的設計區域。子結構是具有內部自由度的超級單元，對地鐵車輛座椅局部的設計區域定義超級單元邊界的自由度。為減少地鐵車輛座椅結構的總自由度，通過靜力凝聚減少子結構內部的自由度。子結構的剛度方程為

KbbKbi

KibKii

ab

ai=Fb

Pi

（4）

式中：ab和ai分別為地鐵車輛座椅子結構的邊界和內部自由度；Fb和Pi分別為地鐵車輛座椅子結構的邊界和內部節點荷載。子結構凝聚后的方程，即超級單元的單元剛度方程為

K*bbab=F*b

（5）

將地鐵車輛座椅子結構的剛度方程加以集成，可以得到簡化的整體剛度方程為

Ka=

P

（6）

式中：

a為地鐵車輛座椅原結構邊界和子結構公共邊界上的節點位移向量；

K為簡化的整體剛度矩陣。地鐵車輛座椅子結構的有限元模型見圖4。

圖 4 子結構有限元模型

2.3 模式重復方法的原理

模式重復使結構模型的某一部分或多個部分的結構與其他部分的結構保持一致，即將設計區域的結構強制生成與主設計區域一致的結構，達到減少制造加工工作量的目的。

在子結構的基礎上進行模式重復時，將4個座椅支架中的1個作為主設計區，另外3個作為從設計區，最終生成結構樣式一致的4個座椅支架。

3 優化結果

3.1 子結構優化結果

將上述目標函數、約束條件和設計變量添加到子結構模型上，得到的模型拓撲優化結果見圖5。由此可見，優化后的座椅支架材料分布不均勻，無法應用到實際的生產加工中。

圖 5 子結構拓撲優化結果

3.2 模式重復優化結果

考慮到設計的4個座椅支架結構應當是一致的，在子結構的基礎上使用模式重復的方法，使優化后的座椅支架結構完全一致，最終的拓撲優化結果見圖6，座椅支架部位有非常清晰的材料分布路線，且材料分布相當均勻。

圖 6 模式重復拓撲優化結果

3.3 模型靜強度計算

根據優化結果對座椅支架進行修改，用優化后的座椅支架替換原始支架，對優化后的整體結構進行靜強度計算，結果見圖7。

圖 7 拓撲優化后的靜強度計算結果， MPa

3.4 結果分析

將原始地鐵車輛座椅整體結構的靜強度計算結果與在子結構基礎上添加模式重復優化后的地鐵車輛座椅整體結構進行對比分析，應力值由201.4 MPa下降到186.1 MPa，減小7%。

4個座椅支架的原始質量為11.84 kg，拓撲優化后的質量為6.01 kg，減輕49%，且優化后的座椅支架得到簡化，最終實現可批量生產的效果。

4 結束語

針對地鐵車輛座椅支架結構，運用子結構和模式重復方法對其進行拓撲優化，對優化后的模型進行靜強度計算，發現結構強度在許用范圍內，優化后座椅支架質量減輕49%且應力值減小7%。與原結構相比，新結構更簡單，傳力路徑更有效，能減輕座椅面的應力集中現象，并最終實現地鐵車輛輕量化。

參考文獻：

[1]KRISHNA M M R. A methodology of using topology optimization in finite element stress analysis to reduce weight of a structure[C]//Proceedings of International Truck & Bus Meeting & Exhibition. Chicago： SAE， 2001.

[2] 吳仕賦. 基于有限元的汽車支架拓撲優化設計[D]. 吉林： 吉林大學， 2005.

[3] 楊天云， 張晴朗， 楊兵， 等. CAE在汽車座椅輕量化設計中的應用[J]. 精密成形工程， 2013， 4（1）： 6-9. DOI： 10.3969/j.issn.1674-6457.2012.01.019.

[4] 丁曉紅， 趙新芳， 王海華， 等. 基于子結構的構件逐步逼近拓撲優化方法研究[J]. 汽車工程， 2014， 36（5）： 638-642.

[5] 王曉明，宋曉文，劉德剛， 等. 動車組行李架支座結構拓撲優化設計[J]. 鐵道車輛， 2013， 51（2）： 11-14. DOI： 10.13462/j.cnki.mmtamt.2017.03.003.

[6] 聶春戈， 李曉峰， 兆文忠. 高速轉向架軸箱轉臂結構拓撲優化設計[J]. 機械設計， 2007， 24（6）： 58-60. DOI： 10.3969/j.issn.1001-2354.2007.06.019.

[7] 高月華， 范錚， 程亞軍， 等. 基于子結構法的動車組設備艙支架優化設計[J]. 大連交通大學學報， 2016， 37（4）： 33-37. DOI： 10.3969/j.issn.1002-7602.2013.02.004.

[8] 吳中博， 李書. 基于Optistruct的結構靜動力拓撲優化設計[J]. 航空計算技術， 2006， 36（6）： 9-12. DOI： 10.3969/j.issn.1671-654X.2006.06.003.

[9] 高鵬飛， 毛虎平， 楊育光， 等. 子結構法在活塞結構優化中的應用[J]. 組合機床與自動化加工技術， 2017（3）： 10-13. DOI： 10.13462/j.cnki.mmtamt.2017.03.003.

[10] KIRSCH U， TAYE S. On optimal topology of grillage structures[J]. Engineering with Computers， 1986， 1（4）： 229-243.

[11] DUYSINX P， BENSE M P. Topological optimization of continuum structures with local stress constraints[J]. International Journal for Numerical Methods in Engineering， 1998， 43（8）： 1453-1478. DOI： 10.1002/（SICI）1097-0207（19981230）43：8<1453：：AID-NME480>3.0.CO；2-2.