小型甘蔗收獲機臺架結構分析與輕量化設計
黃瓊春,李尚平,李 冰,陳 棕,林嘉豪
(1.廣西科技大學 機械工程學院,廣西 柳州 530006 ;2.廣西民族大學 化學化工學院,南寧 530006)
0 引言
甘蔗收獲機是用于甘蔗收割的機械裝置,其良好的工作性能是作物按時、按質收成的良好保證。在不影響甘蔗收獲機正常工作的同時,如何降低甘蔗收獲機的制造成本、減少能源消耗,成為當前研發甘蔗收獲機的一個重要議題。
本文通過優化技術方法對小型甘蔗收獲機樣機臺架進行輕量化設計。首先,建立用以分析的臺架數學模型;然后,以板件厚度為設計變量,建立新的有限元模型。通過模態分析證明,優化后的模型剛性得到加強,臺架的材料得到最優配置。
1 臺架有限元建模
小型甘蔗收獲機是某實驗室自主設計制造,由甘蔗收獲機臺架、物流架、切割系統、液壓系統及行走系統共同組成。甘蔗收獲機臺架通過一定的連接方式與地面、物流架、切割系統相連,在整個機械裝置中主要承受載荷與支撐作用[1]。為了使整個裝置更加輕盈、可靠,在保證強度與剛度要求的同時,對臺架進行尺寸優化設計。
臺架有限元模型是通過三維繪圖軟件建立,然后導入CAE軟件進行建模。臺架主要由槽鋼、角鋼及部分矩形鋼焊接而成。由于臺架大部分由角鋼焊接而成,為了保證單元網格質量,主要使用四邊形、三角形單元對其進行網格劃分,單元大小為10mm。總單元數為46 611,四邊形單元個數為45 678個,三角形單元為307個,以及若干其他單元[2]。模型的材料參數如表1所示,有限元模型如圖1所示。
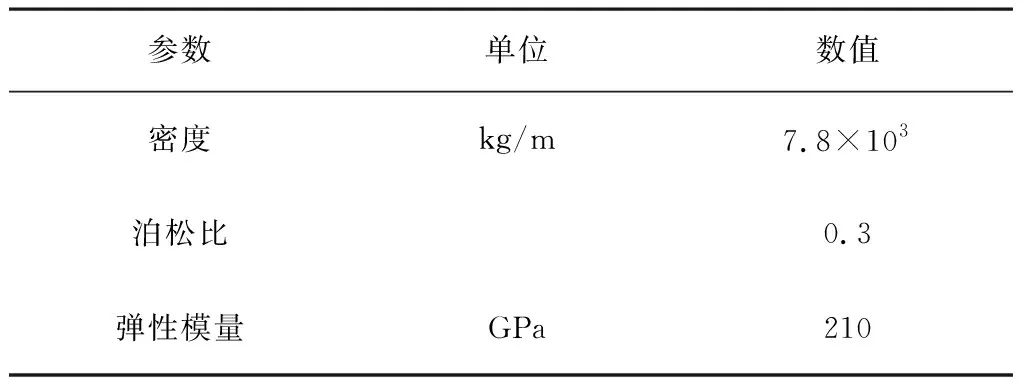
表1 材料屬性參數
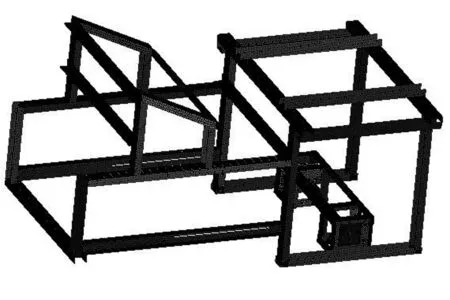
圖1 臺架有限元模型
2 動態特性分析
2.1 模態理論
對于多自由度系統而言,系統的運動微分方程為
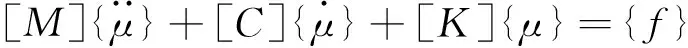
其中,[K]是系統的剛度矩陣;[M]為系統的質量矩陣;[C]為系統的阻尼向量矩陣;{μ}為廣義位移向量;{f}系統的響應向量。本次分析采用的是無阻尼多自由度系統的自由振動,阻尼矩陣[C]與響應向量{f}為0,故上述公式變為
([K]+ω2[M]){φ}={0}
求解上面方程廣義特征值ω2和廣義特征向{φ},即可求得振動的固有頻率和相應的振型[3]。
2.2 有限元分析
由于系統實際約束往往比較復雜,為了更好地求解系統特征方程,利用有限元對臺架進行自由(即無約束)模態分析。在無約束的工況下進行模態分析時,系統的6個自由度的剛體模態便會出現。為了更好地進行模態分析,在此忽略系統的前6階剛體模態及局部模態,得到系統的前4階固有模態階次與振型。限于篇幅,此處給出前兩階模態振型,如圖2、圖3與表2所示。

圖2 臺架第1階彈性模態陣型圖
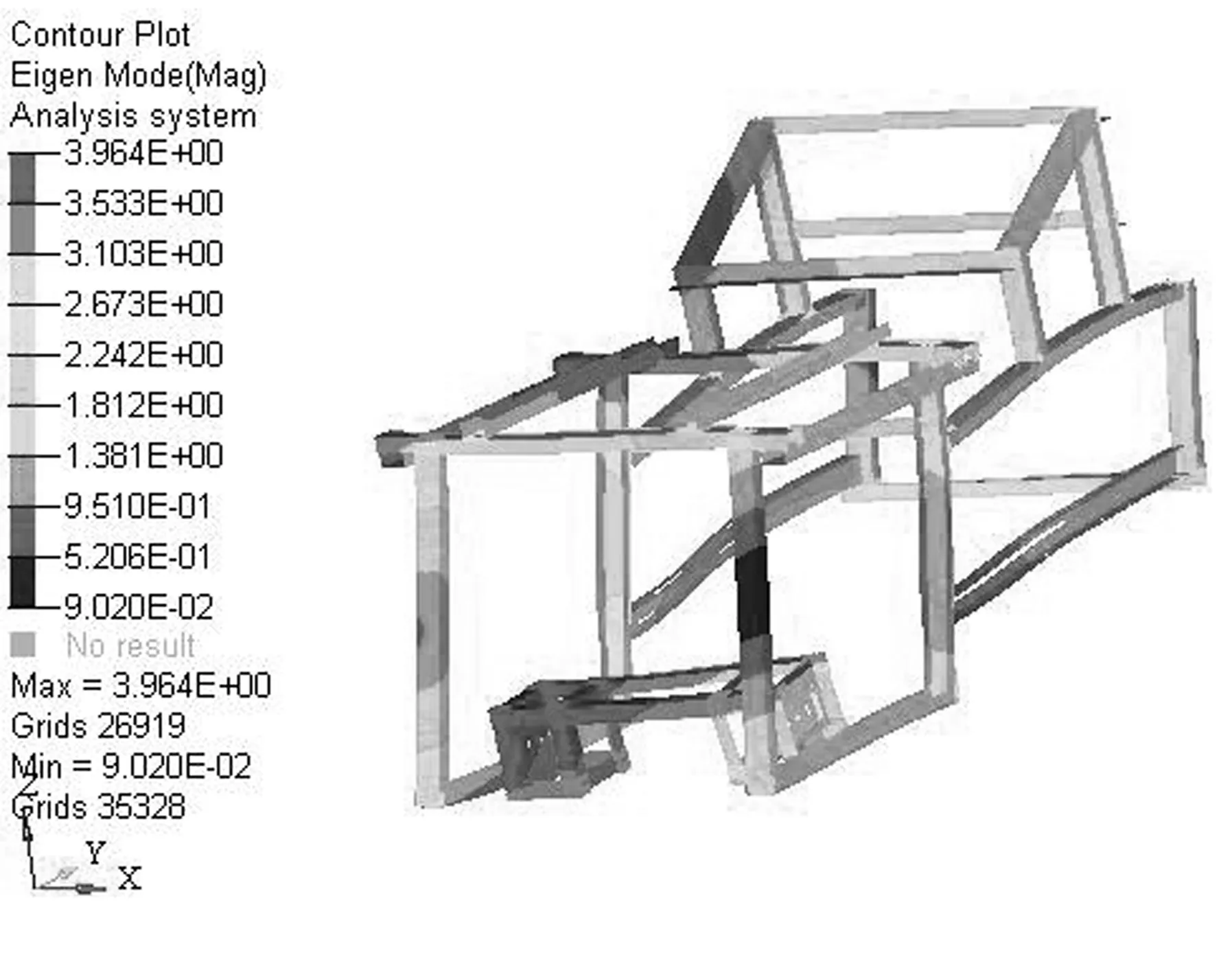
圖3 臺架第2階彈性模態陣型圖
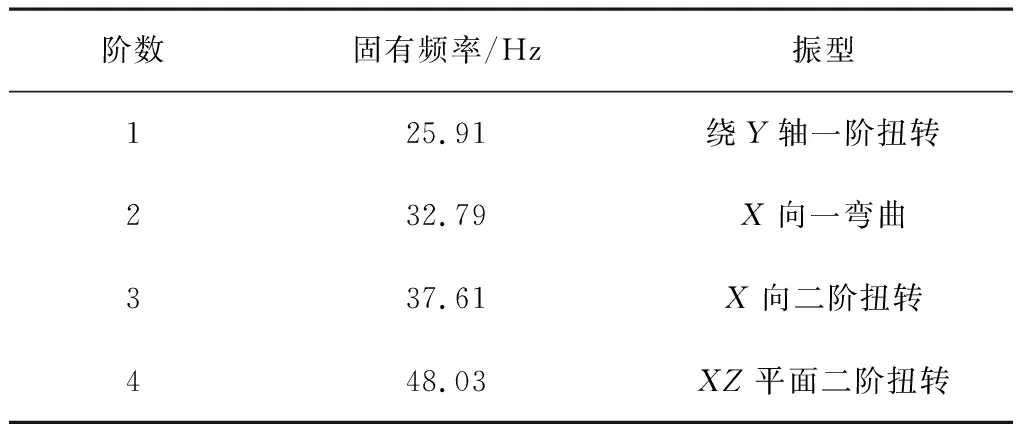
階數固有頻率/Hz振型125.91繞Y軸一階扭轉232.79X向一彎曲337.61X向二階扭轉448.03XZ平面二階扭轉
3 臺架模態試驗
為了得到臺架系統的真實頻率與振型,以了解系統的本身的動態響應,以及對后期的動態特性進行分析,需要對真實系統進行模態實驗。此外,模態實驗能驗證有限元模型的準確性,確保有限元計算結果的精度。本次實驗設備主要有LMS.Lab數據采集前端、PCB三向加速度傳感器及筆記本1臺。本次數據處理運用poly MAX法進行模態參數識別[4]。試驗的過程中,臺架系統的第3階模態丟失,得到系統的第1、第2、第4階振型。由于試驗環境及懸吊測試方式與有限元環境有所區別,故可以允許有限元結果與真實的模態頻率存在一定的誤差[5]。
在對模態實驗數據進行分析時,為了避免選擇重復的模態階次或者避免選擇相近的模態,需要用模態置信(MAC)準則,對選擇的模態階次進行判別。MAC矩陣可表示為

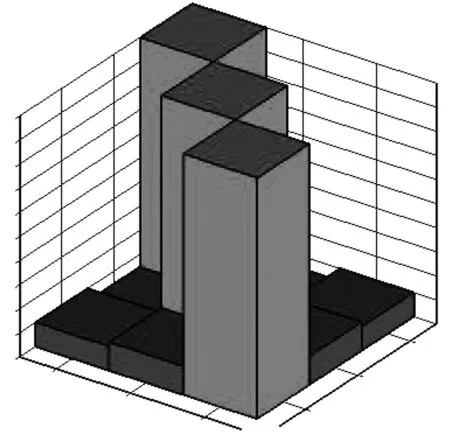
圖4 MAC矩陣圖
利用計算機進行仿真優化可以大大縮減研發的成本及設計的周期,可為很多企業帶來巨大的便利。然而,利用計算機進行優化首要的前提是保證有限元模型的計算結果可用。
經過理論模態與實驗模態可知:兩者的誤差均在9%以內,足以說明有限元模型的正確性,后續可基于此模型進行優化[7]。理論模態與實驗模態的誤差分析如下表3所示。
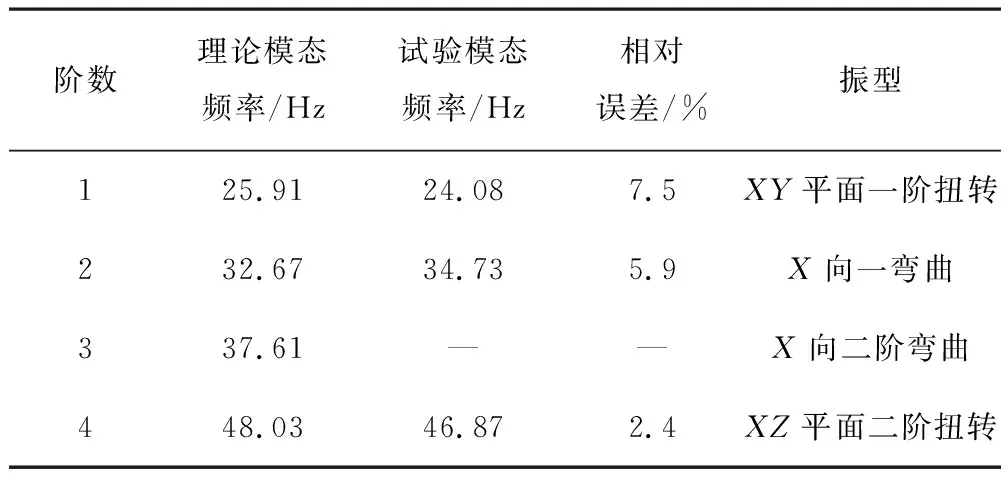
表3 理論模態與試驗模態誤差表
4 臺架結構優化
由于輕量化優化方法在日常中運用甚廣,目前已在各個領域有所運用。輕量化的主要目的為:在滿足結構性能要求時,兼顧制造成本。通過輕量化方法,可以避免材料浪費,使得材料的利用率達到最大化。
尺寸優化的數學模型可表示為
目標函數:minf(X)
約束條件:gj≤0
引入拉格朗日算子:L(X,μ)=f(X)+μTg=f(X)+∑μjgj,故而拉格朗日方程最小化的條件[8]為
▽xL(X)=▽xf(X)+∑μj▽xgj=0
其中,X為設計變量;gj為第j個約束函數;μj為拉格朗日乘子。
4.1 結構優化
現以臺架各個板件厚度為設計變量,以加權特征值倒數最小為目標函數,臺架的質量為約束函數對其進行優化計算。在優化后,對優化尺寸進行取整。優化后的尺寸如圖5所示。

圖5 優化后的尺寸分布數值
通過優化后的結果可知:厚度最大的地方在發動機與駕駛室安裝的位置。由于此處地方存在應力集中,且在工作的過程中承受的彎矩較大,因此是危險位置。這說明,優化后的結果與現實情更加吻合,優化是可靠的。
4.2 方案驗證
將優化后的厚度取整并對原來的尺寸進行修正,將最新的結果按照同樣的約束條件、工況進行計算。優化后的1階模態由原來的25.90Hz變至29.08Hz,增加了12.23%;2階模態由原來的32Hz變至32.79Hz,增加了0.36%。這說明,此次優化使1階固有頻率得到比較好的改善,即改變了發動機與駕駛室的連接位置處的厚度。此外,整個臺架的質量減少了12kg,降低了6%,達到輕量化的目的。1、2階優化前后的對比圖如圖6、圖7所示。
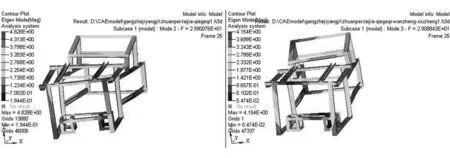
圖6 優化前后1階模態對比
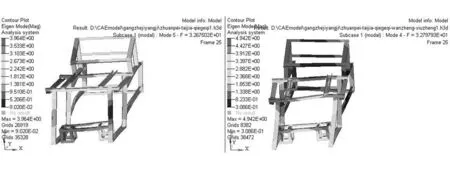
圖7 優化前后2階模態對比
5 結論
1)小型甘蔗收獲機臺架經過尺寸優化后,1階固有頻率由原來的25.91Hz增加到29.08Hz,提升了12.23%;2階固有頻率由32.67增加到32.79,提升了0.36%;臺架的整體質量由178kg降低至166kg,降低了6%。結果表明:以加權特征頻率為目標的尺寸優化技術有效地降低了臺架的質量,提高了系統的動態特性。
2)基于動態特性,以加權特征頻率為目標對小型甘蔗收獲機臺架進行結構優化,并根據優化結果進行模型輕量化設計是行之有效的。
參考文獻:
[1] 葉才福.基于動態特性的砍蔗系統實驗平臺的設計分析[D].南寧:廣西大學,2016.
[2] 李楚琳,張勝蘭,馮櫻,等.Hyperworks分析與運用實例[M].北京:機械工業出版社,2008:97-101.
[3] 李學修.輕卡車身模態分析及其結構優化[D].上海:上海交通大學,2007.
[4] 花勇.基于Hypermesh與ANSYS的農用車車架模態分析[J].現代農業裝備,2013,8(1):43-47.
[5] 靳暢,周鋐.應用 Poly MAX 法的副車架試驗模態以及相關性分析[C]//2008 年 LMS 中國用戶大會論文集.Louvain:LMS,2008.
[6] Shung H. Sung, Donald J. Nefske.Assessmentof a Vehicle Concept Finite-Element Model for Predicting Structural Vibration[J].SAE Paper,2001,1(1):1042-1048.
[7] Gupta C P, Oduori M F. Design of the Revolving Knife-type Sugarcane Basecutter[J]. Transactions of the Asae,1992,35(6):1747-1752.
[8] 孫靖民,梁迎春.機械優化設計[M].北京:機械工業出版社,2006:33-36.

