凸組合實時判決反饋稀疏水聲信道盲均衡算法

肖 瑛，董玉華(大連民族大學 信息與通信工程學院，遼寧 大連 116605)

由于聲波在水介質中傳播的特殊性，目前單載波自適應均衡仍然是水聲通信接收端消除碼間干擾的主要技術手段[1]。隨著海洋資源開發以及軍事發展需求，水聲通信正向著高速高質量需求方向發展，高速水聲通信條件下，水聲信道呈現典型的稀疏特性[2]。對于稀疏水聲信道而言，沖激響應由較短的前達響應和很長的后達響應(拖尾)組成[3]。在高速水聲通信系統中，后達響應表現為時延擴展很長，可達數百個碼元，但是僅有很少的系數攜帶重要能量，其他大部分權系數為零，這使得具備稀疏特性的多徑水聲信道的碼間干擾較之一般水聲信道不同。稀疏水聲信道產生的碼間干擾主要由其時延可達數百個碼元的拖尾響應引起，已經證明線性均衡器長度需要達到信道長度的4倍以上才能逼近理想均衡條件[4]，因此對于稀疏水聲信道線性均衡器要設置足夠長度來獲得理想的均衡性能。而自適應均衡算法計算量與均衡器長度成正比，這直接導致計算復雜度增加。即使采用判決反饋均衡器，其前饋濾波器不需要接近信道的逆，但是研究表明判決反饋均衡器的前饋濾波器長度至少等于信道的長度時，才能獲得較為理想的均衡結果[5]，對于稀疏水聲信道的均衡來說，計算復雜度仍然非常大。

為降低稀疏水聲信道均衡的計算復雜度，稀疏化成為一種有效方法[6]。對于傳統自適應均衡技術可利用訓練序列得到信道響應的預先估計，從而在訓練過程中對均衡器進行稀疏化處理，實驗證明稀疏自適應均衡算法可以降低75%-90%的計算量，但是定期發送訓練序列必將占有有限水聲通信帶寬，降低通信效率[7]。對于盲自適應均衡技術，信道響應的預先估計成為難題，從而導致均衡器稀疏化處理變得困難[8]。已有文獻報道的稀疏水聲信道盲均衡算法，均是傳統自適應均衡技術稀疏化方法的推廣，即均衡器在全階更新一段時間后，設定能量閾值對均衡器進行稀疏化處理[9]。然而對于稀疏水聲信道盲均衡算法，稀疏處理后置零的均衡器權系數將在后續迭代過程中無法重啟，即不再參與更新計算，這使得算法僅能適用于固定沖激響應的水聲信道條件，當信道具有時變特征時，此類稀疏水聲信道盲均衡算法性能將嚴重下降，甚至失效。為此，文中提出了一種凸組合實時判決反饋稀疏水聲信道盲均衡算法，盲均衡器分為保持均衡器支路和稀疏均衡器支路，利用保持均衡器能量和權系數的瞬時梯度作為判據，對稀疏均衡器支路對應抽頭進行實時稀疏化處理。算法中避免設置稀疏化閾值，對不同稀疏水聲信道和通信信號具有通用性，且對于時變稀疏水聲信道可以利用保持均衡器支路恢復稀疏均衡器支路置零抽頭系數，使算法對信道具有較強跟蹤能力。最后利用典型稀疏水聲信道對文中提出算法進行了仿真驗證。

1 判決反饋盲均衡算法

判決反饋均衡器為一種典型的非線性均衡器，利用反饋濾波器來抵償信道的非線性特性，從而消除前饋濾波器的剩余碼間干擾。判決反饋均衡器性能優于線性橫向均衡器，可以補償幅度失真，具有最小的噪聲增益，能夠完全均衡不超過其長度的信道。利用判決反饋均衡器結構，前向濾波器不需近似于信道的逆，避免了增強噪聲，反饋濾波器用于去除由先前已檢測符號引起的符號間干擾。判決反饋均衡器的基本思想是：一旦檢測出某個信息符號，由該符號引起的符號間干擾就被估計出來并被預先減去[10]，其基本結構如圖1。

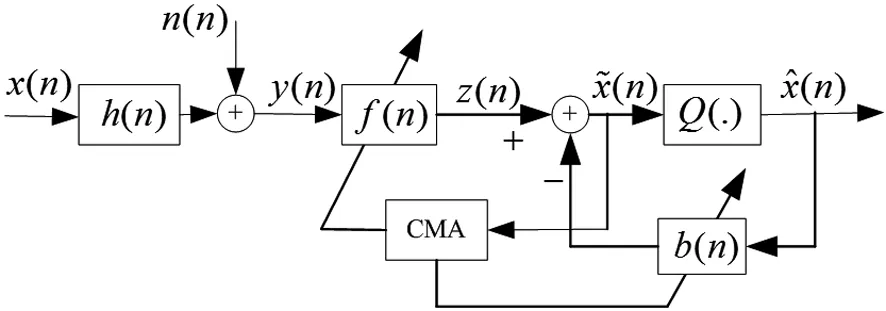
圖1 判決反饋CMA盲均衡示意圖

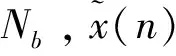
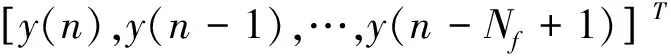
(1)

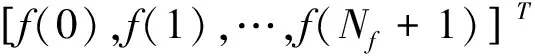
(2)

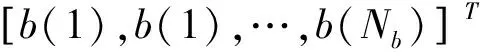
(3)

(4)

則判決反饋均衡器的輸出為

(5)

根據CMA盲均衡代價函數，判決反饋均衡器更新公式為[12]

f(n)=f(n-1)+μfe(n)y*(n)，

(6)

(7)

其中誤差函數按下式計算：

(8)

由于在判決反饋均衡器中，前饋濾波器不需要構成信道的逆信道，即不需要利用前饋濾波器達到理想均衡條件，因此，前饋濾波器的長度僅達到非零有效長度即可，而反饋濾波器長度大于等于信道長度加判決延遲即可。這樣利用判決反饋均衡器對稀疏水聲信道進行均衡，可以有效降低計算復雜度，并利用反饋濾波器抵消前饋濾波器產生的剩余碼間干擾，獲得較優的均衡性能。

2 凸組合判決反饋盲均衡算法

均衡器權稀疏化算法在稀疏水聲信道盲均衡中可以有效降低算法計算復雜度，并在一定程度上提高算法的收斂性能。常用的稀疏化方法依據均衡器抽頭系數能量與預先設定的閾值進行比較，小于設定閾值的均衡器抽頭系數置零完成稀疏化處理。但是，稀疏化閾值的設置對算法性能影響很大，而且閾值的設置只能依賴人工經驗，到目前為止沒有統一合理的設置方法。當稀疏化閾值設置過小時，均衡器權系數幾乎得不到稀疏化處理，算法直接退化為全階均衡算法，當稀疏化閾值設置過大時，有效的均衡器權系數可能會被稀疏化掉，導致均衡性能下降，甚至算法發散。為此提出一種凸組合實時判決反饋稀疏水聲信道盲均衡算法，盲均衡器結構如圖2。其中f1(n)和b1(n)構成稀疏均衡器支路，而f2(n)和b2(n)構成保持均衡器支路，圖2中的雙箭頭虛線表示在一定條件下，保持均衡器支路和稀疏均衡器支路在一定條件下進行交互。這樣整個盲均衡器結構上由兩個獨立的判決反饋均衡器構成，對于稀疏均衡器支路和保持均衡器支路的輸出為

(9)

(10)

而兩路均衡器的更新規則以及誤差函數的計算可以分別依據式(6)-(7)和式(8)進行。

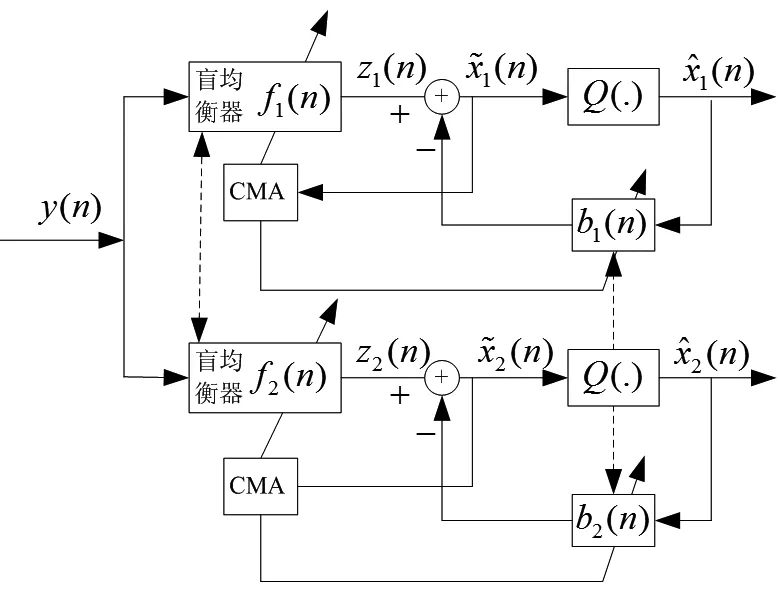
圖2 凸組合判決反饋盲均衡器結構

定義判決反饋均衡器中前饋濾波器和反饋濾波器的權系數能量分別為

(11)

(12)

根據保持均衡器支路，定義前饋濾波器和反饋濾波器的瞬時梯度分別為

(13)

(14)

傳統的稀疏化方法一般是在算法迭代到一定次數后，計算均衡器各個抽頭系數的能量，并將其與給定的閾值進行比較，一旦某抽頭系數的能量小于閾值，則將其置零實現稀疏化處理[13]。這類稀疏化方法的不確定性因素太多，導致算法性能在不同水聲通信條件下不穩定，同時在迭代一定次數后進行稀疏化處理的方式，不僅在降低計算復雜度上不利，同時對于未稀疏化處理的迭代過程中，算法性能與全階均衡算法一致，不能有效提高算法的收斂性能，也不利于對時變稀疏水聲信道的實時跟蹤。這里根據均衡器權系數能量和瞬時梯度，結合凸組合判決反饋盲均衡器給出一種實時稀疏化方法。根據稀疏水聲信道信號傳輸特點，均衡器抽頭系數是否具有顯著能量結合抽頭系數能量和當前瞬時梯度共同判別，即當前抽頭系數能量小于某一閾值，并且對應的瞬時梯度要足夠小，才能判別該抽頭系數應被稀疏化處理。定義均衡器中某一抽頭系數能量為

(15)

(16)

定義均衡器某一抽頭系數的瞬時梯度為

ΔJf2(T)=|e2(n)y*(T)|，

(17)

(18)

當在盲均衡器完成一次迭代后，判斷Ef(T)、Eb(K)與Ef、Eb之間的關系，以及ΔJf(T)、ΔJb(k)與ΔJf2(n)、ΔJb2(n)之間的關系，來共同確定需要稀疏處理的均衡器抽頭系數，稀疏化方法如

(19)

(20)

即對于保持均衡器支路而言，其前饋濾波器某一抽頭系數在某次迭代后，其能量值小于均衡器權系數能量的1/3，并且其對應的更新瞬時梯度小于均衡器總瞬時梯度的1/3時，則稀疏均衡器支路對應的抽頭系數置零實現稀疏化處理。對于反饋濾波器的稀疏化方法與前饋濾波器一致。這樣，保持均衡器支路一直采用全階更新算法，而稀疏均衡器支路在更新過程中實時被稀疏化處理。雖然1/3這個比例數值是經過大量仿真驗證的經驗結果，但是有效避免了閾值設定問題，并且該比例值不受信道、發送信號類型以及噪聲的限制，具有一定的通用性。

如果在整個數據傳輸過程中，一直采用并聯稀疏化處理方法，在稀疏水聲信道條件下將會增加額外的計算復雜度，事實上經過一定步數的迭代，稀疏均衡器就可以實現理想的稀疏化結果。這里以稀疏均衡器支路進入穩態作為判據來決定保持均衡器支路是否再參與更新，稀疏均衡器支路進入穩態以輸出誤差功率來判定。當稀疏信道由于時變產生了性能下降，利用輸出誤差功率的瞬時變化率作為判據來恢復保持均衡器參與更新，以實現稀疏化方法在時變信道中的穩定性。輸出誤差功率的估計采用指數滑動窗估計方法如：

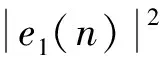
(21)

3 計算機仿真與分析

仿真中采用典型的兩徑稀疏水聲信道模型，信道傳遞函數為

H(z)=1+0.4z-21。

(22)

發送信號為等概率二進制序列，采用QPSK調制方式。前饋濾波器長度為25，中心抽頭系數初始化為1，其余抽頭系數初始化為0，反饋濾波器長度為23，全0初始化。學習步長μ=0.0015。信道噪聲為加性高斯白噪聲，信噪比SNR=20dB。輸出誤差功率估計遺忘因子，λ=0.99。500次蒙特卡洛仿真結果如圖3，凸組合實時判決反饋稀疏盲均衡器的輸出誤差功率曲線如圖4。

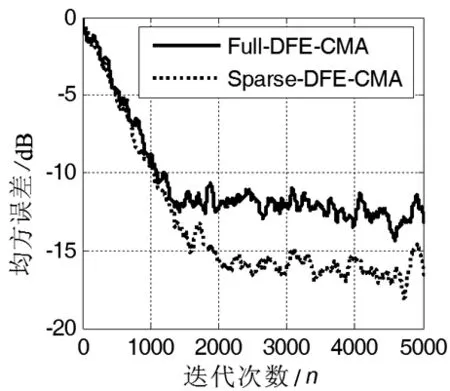
圖3 剩余碼間干擾收斂曲線

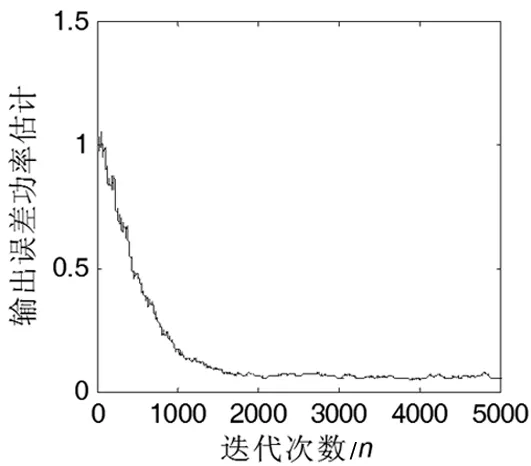
圖4 輸出誤差功率估計曲線

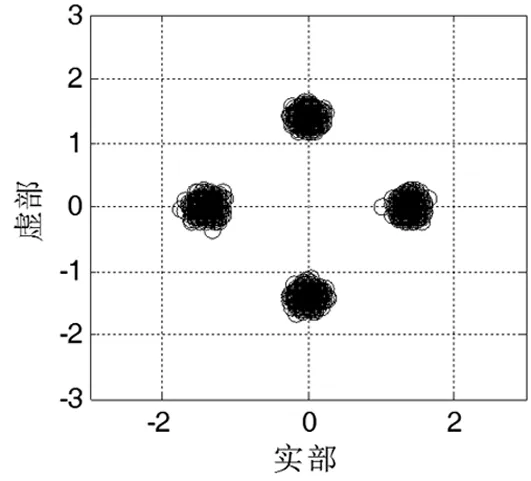
圖5 全階DFE-CMA均衡輸出星座圖

圖6 稀疏DFE-CMA均衡輸出星座圖

從仿真結果圖3中可以看出，凸組合實時判決反饋稀疏盲均衡(Sparse-DFE-CMA)與全階判決反饋盲均衡(Full-DFE-CMA)相比，收斂后穩態剩余誤差下降約5dB，有效提高了均衡性能。由圖3和圖4可知，當輸出誤差功率σ(n)下降到1/3時，即1500次迭代后，均衡器基本進入了穩態狀態，此時，保持均衡器支路停止更新，而稀疏均衡器支路中，前饋濾波器剩余12個有效抽頭系數，反饋濾波器剩余11個有效抽頭系數，算法在1500次迭代后，計算復雜度遠小于全階判決反饋盲均衡算法。圖5和圖6分別給出了Full-DFE-CMA和Sparse-DFE-CMA均衡后輸出的星座圖，可以看出，Sparse-DFE-CMA均衡后星座圖聚斂性要優于Full-DFE-CMA。

4 結 語

文中以稀疏水聲信道盲均衡為研究對象，在對現有稀疏盲均衡算法分析的基礎上，提出了一種凸組合實時判決反饋稀疏盲均衡算法。算法以保持均衡器支路結合抽頭系數能量判別的方式，實現對稀疏均衡器支路的稀疏化處理，算法無需設置稀疏閾值，具有通用性，且保持均衡器支路的引入在時變稀疏水聲信道條件下可以有效避免算法失效。雖然保持均衡器支路在算法起始階段額外增加了計算復雜度，但是對于長時水聲通信而言，增加的計算復雜度僅局限在一定迭代次數范圍內，而稀疏均衡器支路的計算復雜度相比全階判決反饋盲均衡器顯著降低。仿真結果證明了算法的有效性。

參考文獻：

[1] 孫麗君, 孫超. 一種用于水聲信道的稀疏權超指數迭代盲均衡算法研究[J]. 電子與信息學報, 2005, 27(8): 1205-1207.

[2] 張艷萍, 趙俊渭, 李金明. 稀疏水聲信道判決反饋盲均衡算法研究[J]. 電子與信息學報, 2006, 28(6): 1009-1012.

[3] 郭業才, 郭福東, 丁雪杰. 基于正交小波變換的稀疏權盲均衡算法[J]. 數據采集與處理, 2010, 25(5): 569-574.

[4] 田營, 葛臨東, 王彬,等. 一種改進的稀疏多徑信道盲辨識[J]. 信號處理, 2011, 27(7): 1009-1015.

[5] 羅亞松, 胡洪寧. 基于移動抽頭機制的判決反饋盲均衡算法研究[J]. 儀器儀表學報, 2015, 36(1): 63-69.

[6] 周躍海, 曹秀玲, 陳東升,等. 長時延擴展水聲信道的聯合稀疏恢復估計[J]. 通信學報, 2016, 37(2): 165-172.

[7] 張婷, 王彬, 劉世剛. 基于Hammerstein模型的非線性信道廣義線性盲均衡算法[J]. 電子學報, 2015, 43(9): 1723-1731.

[8] HWANG K, CHOI S. Blind equalizer for constant modulus signals based on Gaussian process regression [J]. Signal Processing, 2012, 92(6): 1397-1403.

[9] 郭業才, 林仁剛. 基于T/4分數間隔的判決反饋盲均衡算法研究[J]. 數據采集與處理, 2008, 23(3): 284-287.

[10] GOUPIL A, PALICOT J. An efficient blind decision feedback equalizer [J]. IEEE Communications Letters, 2010, 14(5) : 462-464.

[11] 寧小玲, 劉忠, 羅亞松,等. 一種改進的水聲信道載波恢復盲均衡算法[J]. 西安電子科技大學學報, 2012, 39(1): 151-156.

[12] XIAO Y, YIN F L. Blind equalization based on RLS algorithm using adaptive forgetting factor for underwater acoustic channel [J]. China Ocean Engineering, 2014, 28(3): 401-408.

[13] 楊源, 李明陽, 王徐華. 一種改進的稀疏多徑信道均衡方法[J]. 西安電子科技大學學報, 2014, 41(1): 158-163.