整體視域下小數教學“三維體系”的構建

曹志國

摘 要：數的認識是學生學習數的運算、研究數量關系的重要基礎，而小數的認識是其中的核心內容之一。小數的教學，要站在更為宏觀的層面，基于整體性視域，樹立結構化的意識，關注數系、計數法和運算規則“三維體系”的構建，促進學生的全面與深度認知，助推良好數學素養的形成。

關鍵詞：小學數學；小數教學；整體視域；結構體系

中圖分類號：G623.5 文獻標識碼：A 文章編號：1009-010X（2018）13-0026-03

數的認識是學生學習數的運算、研究數量關系的重要基礎，而小數的認識是其中的核心內容之一。《義務教育數學課程標準（2011版）》在課程目標中提出了經歷從日常生活中抽象出數的過程，初步認識小數，理解小數的意義，掌握必要的運算技能等目標。廣大教師在教學時，一般只將小數的意義作為核心內容，并將讀寫、大小比較、四則計算等作為重點內容展開教學。

然而建構主義認為：“認識必定是一個整合的過程，即如何把新的對象納入已有的認知結構之中，從而使全部知識匯成一個整體。”筆者以為，要真正實現課標中提出的理解小數的意義等目標，還需要“跳出”小數開展小數教學，基于整體性視域，站在更為宏觀的層面，適時建構小學與整數、分數等之間的聯接，呈現更為系統的知識結構，促進學生認知結構的形成。

一、關注數系的構建

在中小學數學中，從自然數開始到復數集的建立，數系經歷了四次擴充（主要是逐步添加元素并強調運算可施行），其擴充過程是：自然數（添正分數）→非負有理數（添負有理數）→有理數（添無理數）→實數（添虛數）→復數。數系的每一次擴充，都擴大了數的應用范圍。小數和分數的擴充，增強了現實世界中對數量表達的能力，使整體中的“部分”在無法用自然數表示時，有了刻畫的方式，也使除法運算得以封閉。

其實，分數與有限小數或者無限循環小數之間是對應等價的。我們可以用小數定義有理數，即為有限小數或者無限循環小數。進一步，將無限不循環小數稱為無理數。進而，就可以用小數定義實數，有理數和無理數統稱為實數。

現行各版本教材在認識小數內容編排時，也都或多或少地對小數的諸多種概念進行了介紹。比如，五年級上冊“小數的乘法和除法”單元的最后以“你知道嗎”的方式，介紹了有限小數、無限小數、循環小數等概念，意圖向學生傳遞小數知識，拓寬對小數的全面認識。但在實踐中，對“你知道嗎”的教學常常停留于閱讀的層面，導致“水過地皮濕”，學生閱讀之后，什么印象也沒有。

為提升教學效果，應充分依托“你知道嗎”等教學資源，組織探索性、研究性活動，引發深度學習，幫助學生建構更為全面的數概念。教學中，可呈現商為整數、有限小數、無限小數等多例除法豎式，學生小組合作計算結果，并以小數的位數的多少為標準對結果進行分類。之后，教師再適時介紹有限小數、循環小數、有理數。再由祖沖之的故事引入π，呈現當代數學家已將圓周率算到小數點后幾萬億位以及有的數學愛好者能一口氣背出圓周率小數部分很多位等素材，并對黃金分割及希帕索斯被害致死的故事等進行介紹，生成無限不循環小數、無理數、實數等概念。學生雖然暫時還不能完全理解上述概念，但他們能真切地感受到人類對數學知識的不懈追求，在不知不覺中走進了更為廣闊的數的世界，更為宏觀的數系概念也已悄然孕育，激發了他們對于數學學科的濃厚興趣。

二、關注計數法體系的構建

2000年度國家最高科學技術獎獲得者吳文俊院士在其著作《吳文俊論數學機械化》中寫道：“位值制的數字表示方法極其簡單，因而也掩蓋了他的偉大業績……這一發明對人類文化貢獻之巨，縱然不能與火的發明相比，至少是可與文化史上我國的四大發明相媲美的。中華民族應以這一發明而自豪。”史寧中教授指出：“在小學階段，理解小數的重點在于對于十進制的認識。”小數教學，應著力構建小數計數單位之間的十進關系，并打通其與整數之間十進關系的聯接，構建十進制計數法體系，充分感悟這一數學史上“最妙的發明之一”。

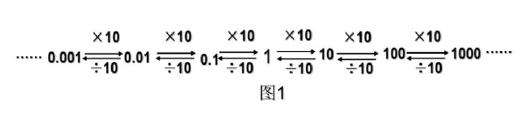
在認識多位數時， 學生已經掌握“10個一是十”“10個十是百”“10個百是千”……生活中，學生對小數計數單位及其之間的關系雖有著感性認識，但缺乏理性認知，系統性則更是缺乏。而小數的表征形式與自然數相似，都是十進制，小數部分相鄰的計數單位之間，以及十分位和個位的計數單位之間，進率都是10。自然數、小數互聯的十進制計數法體系的構建，使十進制的進率方向具有“雙向性”。向右不斷乘10，計數單位可以無限大；向左不斷除以10，計數單位可以無限小；一左一右的延伸，使學生對數的認識更為全面系統。體系的構建處于學生的最近發展區內，促進了對十進制的深度認知，揭示了十進制計數法的深刻內涵。

三、關注運算規則體系的構建

數學教學中應力求呈現數學動態統一的、有機關聯的、鮮活生動的、具有探索性的和全息性知識特征的科學與文化形象，而不是固定不變的、僵化教條的、局部的、彼此分割的知識條塊和記憶庫。數的運算中很多內容互相依存、彼此關聯，存在著嚴密的邏輯性。教學中，要找尋小數與整數、分數四則運算之間的“共同規則”，將多個“規則單一體”整合成“規則共同體”，實現表征系統間的互相轉換，使規則交叉融合，結成網、連成片，構建運算規則結構系統。

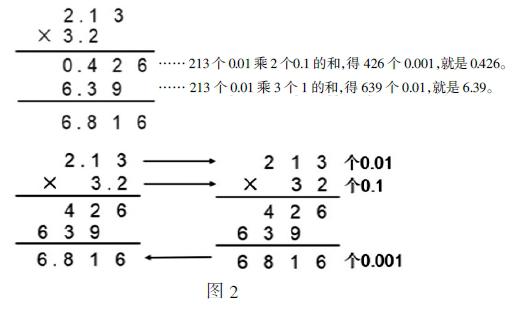
教學中，要依據算理進行算法教學，使學生厘清整數加、減法的豎式計算時，將個位對齊；小數加、減法的豎式計算要把小數點對齊；分數加減法中需要先通分；其原理其實都是一樣的，本質上是把相同計數單位的個數相加減。列豎式計算小數乘法中，小數點對齊法或末尾對齊法（圖2），就是將計數單位再統一，計算的是統一之后的計數單位的個數。當然，從算法優化的角度看，末尾對齊法更為方便、不易出錯。

在此基礎上，將其與整數乘法規則（圖3）再進一步統一：不論是整數乘法、還是小數乘法，都是計算乘積中所包含的新的、統一的計數單位的個數，再根據包含的新的計數單位的個數，寫出最后的結果。當然，站在算法統一的角度，還要適時溝通小數除法與小數乘法之間的聯系，它們都是轉化為整數乘、除法之后再進行運算。計算規則的統一，學生在頭腦中產生了新的綜合心理圖式，構建了更為清晰、完整和穩固規則系統，走進了數學的知識本源與精神內核。

當然，十進制計數法、運算規則、尤其是數系等“三維體系”的建立，需要循序漸進。從知識結構內化為學生的認知結構，也不可能一蹴而就。但教師要有“從點到面”更為寬廣的整體教學視域，要有“結構化”的意識與實踐自覺，促進學生的全面認知與深度認知，助推學生良好數學素養的形成。

參考文獻：

[1]沈重予，王 林.小學數學內容分析與教學指導[M].南京：江蘇鳳凰教育出版社，2015：55.

[2]黃秦安，曹一鳴.數學教育原理——哲學、文化與社會的視角[M].北京：北京師范大學出版社，2010：67.